山东省菏泽市定陶区2020-2021学年度中学联盟第一学期期中学业水平测试九年级数学试题(图片版,附word版答案)
文档属性
| 名称 | 山东省菏泽市定陶区2020-2021学年度中学联盟第一学期期中学业水平测试九年级数学试题(图片版,附word版答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-01 11:47:57 | ||
图片预览

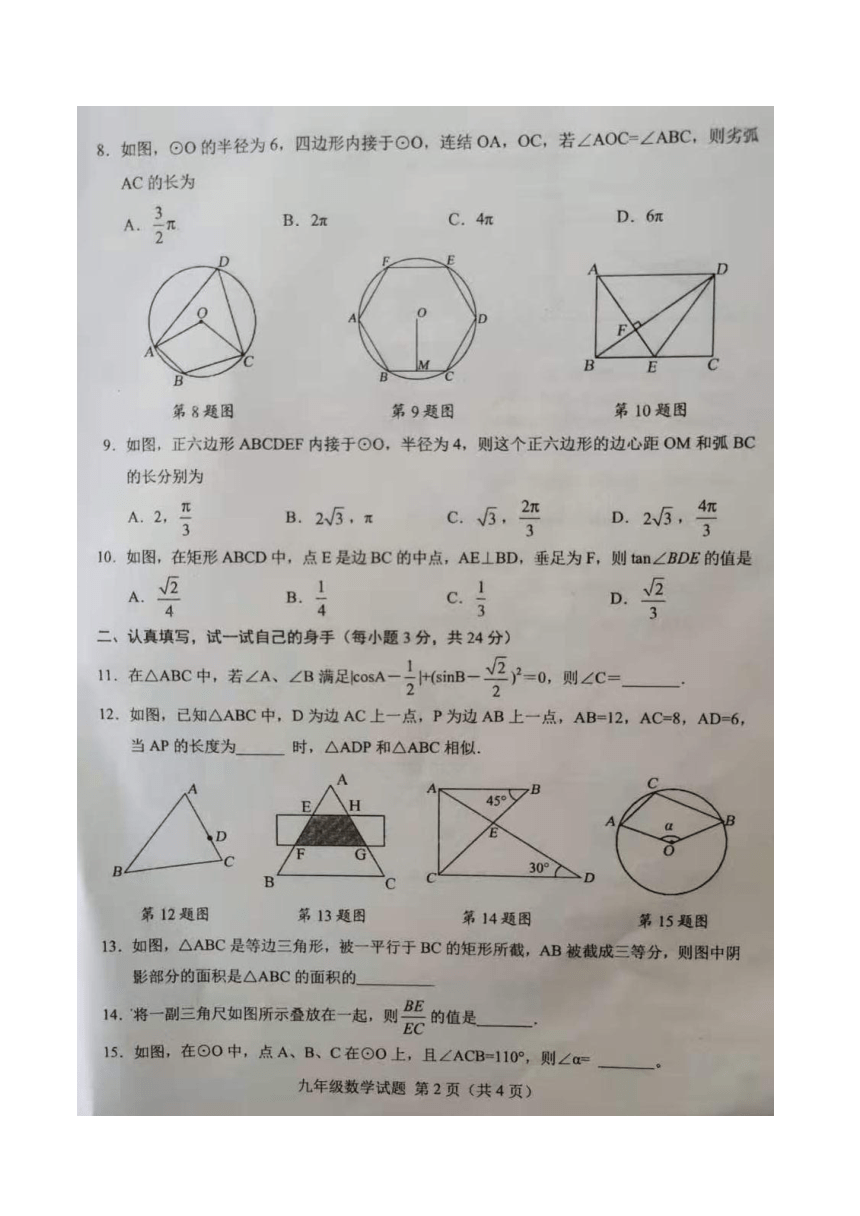

文档简介
1108710010515600
九年级数学答案
(答案仅供参考,请同组阅卷老师核实答案后再阅卷)
选择题
B 2、D 3、C 4、 A 5、C 6、C 7、D 8、 C 9、D 10、A
53568601842770二、11、75° 12、4或9 13、 13 14、 33 15、140° 16 、154 17、 32 18、π2
三、解答题(不写过程者不得分,证明或解答过程不唯一者,合理即可)
19、(过程略)(1)false-1,(2)1
20、(1)证明:∵CE=CD, ∴∠CDE=∠CED. ∴∠ADB=∠CEA.
∵∠DAC=∠B, ∴△ABD ∽△CAE.
(2)解:由(1)△ABD∽△CAE, ∴false. ∵AB=6,AC=false,BD=2, ∴AE=false.
21、(1)∵直径AB⊥CD, ∴弧BC= 弧BD
∴∠DCB=∠CAB=30度;
(2)∵直径AB⊥CD,CD=6cm, ∴CE=3cm, 在Rt△ACE中,∠A=30°, ∴AC=6cm,
∵AB是直径, ∴∠ACB=90°, 在Rt△ACB中,AB=ACcos∠A = 43
22、(过程略)40033米
23、延长AD交BC的延长线于E,作DF⊥BE于F, ∵∠BCD=150°,∴∠DCF=30°,又CD=4,
∴DF=2,CF=23 由题意得∠E=30°, ∴EF=23 ∴BE=BC+CF+EF=6+43
∴AB=BE×tanE=(6+43)×33 =(23+4)米
48748957918450答:电线杆的高度为(23+4)米
(1)过点F作,交BC于点M,
∵F为AB的中点, ∴M为BC的中点,false,
由,得false,false , ∴
∴false ∴false
∴false;
(2)(过程略)27
解答?(1)证明:连接OD,∵D为弧BC的中点,
∴∠CAD=∠BAD, ∵OA=OD, ∴∠BAD=∠ADO,∴∠CAD=∠ADO,
∵DE⊥AC, ∴∠E=90°, ∴∠CAD+∠EDA=90°,即∠ADO+∠EDA=90°,
∴OD⊥EF, ∴EF为半圆O的切线;
(2)解:连接OC与CD, ∵DA=DF, ∴∠BAD=∠F, ∴∠BAD=∠F=∠CAD,
又∵∠BAD+∠CAD+∠F=90°, ∴∠F=30°,∠BAC=60°, ∵OC=OA,
∴△AOC为等边三角形, ∴∠AOC=60°,∠COB=120°,
∵OD⊥EF,∠F=30°, ∴∠DOF=60°,
在Rt△ODF中,DF=6false, ∴OD=DF?tan30°=6,
在Rt△AED中,DA=6false,∠CAD=30°,
∴DE=DA?sin30°false,EA=DA?cos30°=9,
∵∠COD=180°-∠AOC-∠DOF=60°, ∴CD∥AB, 故S△ACD=S△COD,
∴S阴影=S△AED-S扇形COD = 2732 - 6π
26、解:(1)在△ABC中,∵AB=AC, ∴∠ABC=∠C。
∵DE∥BC,∴∠ABC=∠E, ∴∠E=∠C。 又∵∠ADB=∠C, ∴∠ADB=∠E。
(2)解:∵∠baiABC=∠AED,∠ABC=∠ACB,∠ADB=∠ACB
∴∠ADB=∠E,∠BAD=∠BAD, ∴△ABD∽△ADE, ∴ ABAD = ADAE
又AB=6,BE=3, ∴AD=false
(3)当点D是弧BC的中点时,DE是⊙O的切线。
∵当点D是弧BC的中点时,AD⊥BC,且AD过圆心O
又∵DE∥BC,∴ AD⊥ED。 ∴ DE是⊙O的切线。
九年级数学答案
(答案仅供参考,请同组阅卷老师核实答案后再阅卷)
选择题
B 2、D 3、C 4、 A 5、C 6、C 7、D 8、 C 9、D 10、A
53568601842770二、11、75° 12、4或9 13、 13 14、 33 15、140° 16 、154 17、 32 18、π2
三、解答题(不写过程者不得分,证明或解答过程不唯一者,合理即可)
19、(过程略)(1)false-1,(2)1
20、(1)证明:∵CE=CD, ∴∠CDE=∠CED. ∴∠ADB=∠CEA.
∵∠DAC=∠B, ∴△ABD ∽△CAE.
(2)解:由(1)△ABD∽△CAE, ∴false. ∵AB=6,AC=false,BD=2, ∴AE=false.
21、(1)∵直径AB⊥CD, ∴弧BC= 弧BD
∴∠DCB=∠CAB=30度;
(2)∵直径AB⊥CD,CD=6cm, ∴CE=3cm, 在Rt△ACE中,∠A=30°, ∴AC=6cm,
∵AB是直径, ∴∠ACB=90°, 在Rt△ACB中,AB=ACcos∠A = 43
22、(过程略)40033米
23、延长AD交BC的延长线于E,作DF⊥BE于F, ∵∠BCD=150°,∴∠DCF=30°,又CD=4,
∴DF=2,CF=23 由题意得∠E=30°, ∴EF=23 ∴BE=BC+CF+EF=6+43
∴AB=BE×tanE=(6+43)×33 =(23+4)米
48748957918450答:电线杆的高度为(23+4)米
(1)过点F作,交BC于点M,
∵F为AB的中点, ∴M为BC的中点,false,
由,得false,false , ∴
∴false ∴false
∴false;
(2)(过程略)27
解答?(1)证明:连接OD,∵D为弧BC的中点,
∴∠CAD=∠BAD, ∵OA=OD, ∴∠BAD=∠ADO,∴∠CAD=∠ADO,
∵DE⊥AC, ∴∠E=90°, ∴∠CAD+∠EDA=90°,即∠ADO+∠EDA=90°,
∴OD⊥EF, ∴EF为半圆O的切线;
(2)解:连接OC与CD, ∵DA=DF, ∴∠BAD=∠F, ∴∠BAD=∠F=∠CAD,
又∵∠BAD+∠CAD+∠F=90°, ∴∠F=30°,∠BAC=60°, ∵OC=OA,
∴△AOC为等边三角形, ∴∠AOC=60°,∠COB=120°,
∵OD⊥EF,∠F=30°, ∴∠DOF=60°,
在Rt△ODF中,DF=6false, ∴OD=DF?tan30°=6,
在Rt△AED中,DA=6false,∠CAD=30°,
∴DE=DA?sin30°false,EA=DA?cos30°=9,
∵∠COD=180°-∠AOC-∠DOF=60°, ∴CD∥AB, 故S△ACD=S△COD,
∴S阴影=S△AED-S扇形COD = 2732 - 6π
26、解:(1)在△ABC中,∵AB=AC, ∴∠ABC=∠C。
∵DE∥BC,∴∠ABC=∠E, ∴∠E=∠C。 又∵∠ADB=∠C, ∴∠ADB=∠E。
(2)解:∵∠baiABC=∠AED,∠ABC=∠ACB,∠ADB=∠ACB
∴∠ADB=∠E,∠BAD=∠BAD, ∴△ABD∽△ADE, ∴ ABAD = ADAE
又AB=6,BE=3, ∴AD=false
(3)当点D是弧BC的中点时,DE是⊙O的切线。
∵当点D是弧BC的中点时,AD⊥BC,且AD过圆心O
又∵DE∥BC,∴ AD⊥ED。 ∴ DE是⊙O的切线。
同课章节目录
