安徽合肥市高新区四校2020-2021第一学期九年级期中数学试卷(word版含答案)
文档属性
| 名称 | 安徽合肥市高新区四校2020-2021第一学期九年级期中数学试卷(word版含答案) | 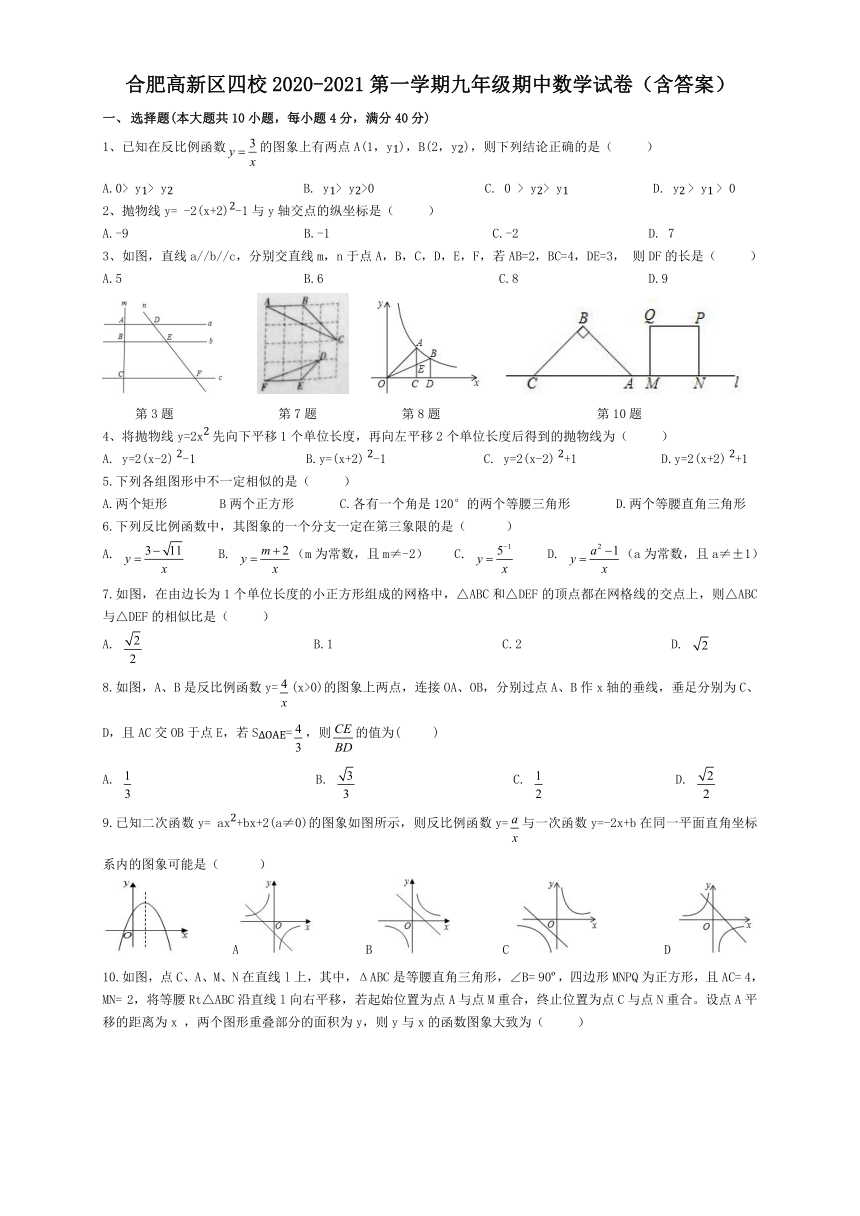 | |
| 格式 | doc | ||
| 文件大小 | 240.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-01 13:07:55 | ||
图片预览


文档简介
合肥高新区四校2020-2021第一学期九年级期中数学试卷(含答案)
选择题(本大题共10小题,每小题4分,满分40分)
1、已知在反比例函数的图象上有两点A(1,y1),B(2,y2),则下列结论正确的是( )
A.0> y1> y2 B. y1> y2>0 C. 0 > y2> y1 D. y2 > y1 > 0
2、抛物线y= -2(x+2)2-1与y轴交点的纵坐标是( )
A.-9 B.-1 C.-2 D. 7
3、如图,直线a//b//c,分别交直线m,n于点A,B,C,D,E,F,若AB=2,BC=4,DE=3, 则DF的长是( )
A.5 B.6 C.8 D.9
第3题 第7题 第8题 第10题
4、将抛物线y=2x2先向下平移1个单位长度,再向左平移2个单位长度后得到的抛物线为( )
A. y=2(x-2) 2-1 B.y=(x+2) 2-1 C. y=2(x-2) 2+1 D.y=2(x+2) 2+1
5.下列各组图形中不一定相似的是( )
A.两个矩形 B两个正方形 C.各有一个角是120°的两个等腰三角形 D.两个等腰直角三角形
6.下列反比例函数中,其图象的一个分支一定在第三象限的是( )
A. B. (m为常数,且m≠-2) C. D. (a为常数,且a≠±1)
7.如图,在由边长为1个单位长度的小正方形组成的网格中,△ABC和△DEF的顶点都在网格线的交点上,则△ABC与△DEF的相似比是( )
A. B.1 C.2 D.
8.如图,A、B是反比例函数y=(x>0)的图象上两点,连接OA、OB,分别过点A、B作x轴的垂线,垂足分别为C、D,且AC交OB于点E,若SΔOAE=,则的值为( )
A. B. C. D.
9.已知二次函数y= ax2+bx+2(a≠0)的图象如图所示,则反比例函数y=与一次函数y=-2x+b在同一平面直角坐标系内的图象可能是( )
A B C D
10.如图,点C、A、M、N在直线l上,其中,ΔABC是等腰直角三角形,∠B= 90?,四边形MNPQ为正方形,且AC= 4,MN= 2,将等腰Rt△ABC沿直线l向右平移,若起始位置为点A与点M重合,终止位置为点C与点N重合。设点A平移的距离为x ,两个图形重叠部分的面积为y,则y与x的函数图象大致为( )
A B C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若反比例函数y=的图象经过点(1,-3),则k的值为 .
12.已知△ABC∽A'B'C,AB=2,A'B'=6,则△ABC与△A'B'C的周长之比为 .
13.如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与矩形OABC的边
AB交于点E,且AE:EB=1:2,则矩形OABC的面积为 .
14.已知二次函数y=-x2+(m-1)x+m(m为常数)。
(1)该函数图象与x轴交点的个数是 .
(2)当一2≤m≤4时,该函数图象的顶点纵坐标y?的取值范围是 .
三、(本大题共2小题,每小题8分,满分16分)
15. 如图,D是△ABC的边AB上的一点,BD=4,AB=9,BC=6.求证:△BCD∽△BAC.
16.小明要把一篇文章录人电脑,所需时间y(分)与录入文字的速度x(字/分)之间的反比例函数关系如图所示。
(1)这篇文章共有 个字,y 与x的函数表达式为 .
(2)若小明7点30分开始录入,预计完成时间不超过7点42分,请结合雨数的性质,求小明录人文字速度的最小值。
四、(本大题共2小题,每小题8分,满分16分)
17.若,a+b+c=27,求a的值。
18.如图,二次函数y=x2-x-2的图象与x轴交于A,B两点(点A在点B的左侧).
(1)若P(-2,m)为二次函数y=x2-x- 2的图象上-点,求m的值; (2)求AB的长.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在△ABC中,AB=AC=10,BC=6,点P从点B出发以1个单位/秒的速度向点A运动,同时点Q从点C出发以2个单位/秒的速度向点B运动,当一点到达终点后,另一点也停止运动。求当运动时间为多少秒时,以B、P、Q为顶点的三角形与△ABC相似?
20.如图,反比例函数为y1=上的图象与一次函数y2=x+b的图象交于A、B两点,其中A点坐标为(1,3),B点的横坐标为-3.
(1)k= , b= .
(2)观察图象可知,当y1< y2时,自变量x的取值范围为 .
(3)一次函数的图象与y轴交于点C,点P是反比例函数图象上的一个动点,若SΔOCP=6,求此时P点的坐标。
六、(本题满分12分)
21.某水果店购进某品种榴莲,榴莲的保质期为30天,平均每颗榴莲的售价为100元,由于榴莲需要冷藏保存,
因此成本也会逐日增加,第x天时,每颗榴莲的成本为y元,y与x的函数关系如图所示。
该榴莲每天的销售量为m颗,m与x之间的关系如下表所示:
第x天 1≤x≤16 16<x≤30
每天的销售量m/颗 15 x+10
(1)求y与x的函数表达.
(2)若每天的销售利润为W元,求w与x的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是
多少元?
七、(本题满分12分)
22.已知抛物线y=ax2+bx-3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,连接BC.
(1)填空:a= ,b= .
(2)如图,若D为直线BC下方抛物线上一动点(不与点C,B 重合),连接OD交BC于点E,求的最大值.
八、(本题满分14分)
23.如图,已知E、F分别为正方形ABCD边CD、AD的中点,BE,CF交于点P。
(1)求证:△DFC≌ΔCEB; (2)求证:BC2=BP?BE; (3)猜想AP与AB是否相等,并给出证明.
合肥市高新区四校2020-2021第一学期九年级期中数学试卷答案
1 2 3 4 5 6 7 8 9 10
B A D B A C D B A C
11、 -1; 12、 1:3; 13、 6; 14、 (1) 1或2; (2) 0≤y?≤
15、∵BD=4,AB=9;∴AD=5,BD:BC=4:6=2:3,BC:AB=6:9=2:3,∴BD:BC= BC:AB,
又∠B=∠B,∴△BCD∽△BAC;
16、(1)1500; ; (2)速度最小值为125字/分;
17、 6; 18、(1)4; (2)3; 19、或;
20、(1)k=3; b=2; (2)x>1或-3<x<0; (3)P(6,)或(-6,)
21、(1)y=x+60; (2)第17天利润最大,最大为621元;
22、(1)a=1; b=-2; (2);
23、(1)∵E、F分别为正方形ABCD边CD、AD的中点,∴BC=CD,CE=DF,∠BCE=∠CDF;∴△DFC≌ΔCEB;
(2)由(1)△DFC≌ΔCEB;∴∠CBE=∠DCF;∴∠CBF+∠BCP=90°,即∠BPC=90°,∴∠BPC=∠BCE;
∠CBP=∠EBC;∴△PBC∽ΔCBE;∴BP:BC=BC:BE,即BC2=BP?BE;
(3)过点A作AG⊥BP,垂足为G,设正方形ABCD边长为2a;由(1)得FC=BE=a;同时∠AGB=∠CDF=90°,
∠ABG=∠CFD;∴△AGB∽ΔCDF;∴BG:DF=AB:FC,即BG:a=2a:a,∴BG=a;
又:∠CPE=∠CDF=90°,∠ECP=∠FCD;∴△PCE∽ΔDCF;∴EP:DF=CE:FC,即BG:a=a:a,∴EP=a;
∴PG=BE-EP-BG=a=BG;则AG为线段BP的垂直平分线,即AP=AB。
选择题(本大题共10小题,每小题4分,满分40分)
1、已知在反比例函数的图象上有两点A(1,y1),B(2,y2),则下列结论正确的是( )
A.0> y1> y2 B. y1> y2>0 C. 0 > y2> y1 D. y2 > y1 > 0
2、抛物线y= -2(x+2)2-1与y轴交点的纵坐标是( )
A.-9 B.-1 C.-2 D. 7
3、如图,直线a//b//c,分别交直线m,n于点A,B,C,D,E,F,若AB=2,BC=4,DE=3, 则DF的长是( )
A.5 B.6 C.8 D.9
第3题 第7题 第8题 第10题
4、将抛物线y=2x2先向下平移1个单位长度,再向左平移2个单位长度后得到的抛物线为( )
A. y=2(x-2) 2-1 B.y=(x+2) 2-1 C. y=2(x-2) 2+1 D.y=2(x+2) 2+1
5.下列各组图形中不一定相似的是( )
A.两个矩形 B两个正方形 C.各有一个角是120°的两个等腰三角形 D.两个等腰直角三角形
6.下列反比例函数中,其图象的一个分支一定在第三象限的是( )
A. B. (m为常数,且m≠-2) C. D. (a为常数,且a≠±1)
7.如图,在由边长为1个单位长度的小正方形组成的网格中,△ABC和△DEF的顶点都在网格线的交点上,则△ABC与△DEF的相似比是( )
A. B.1 C.2 D.
8.如图,A、B是反比例函数y=(x>0)的图象上两点,连接OA、OB,分别过点A、B作x轴的垂线,垂足分别为C、D,且AC交OB于点E,若SΔOAE=,则的值为( )
A. B. C. D.
9.已知二次函数y= ax2+bx+2(a≠0)的图象如图所示,则反比例函数y=与一次函数y=-2x+b在同一平面直角坐标系内的图象可能是( )
A B C D
10.如图,点C、A、M、N在直线l上,其中,ΔABC是等腰直角三角形,∠B= 90?,四边形MNPQ为正方形,且AC= 4,MN= 2,将等腰Rt△ABC沿直线l向右平移,若起始位置为点A与点M重合,终止位置为点C与点N重合。设点A平移的距离为x ,两个图形重叠部分的面积为y,则y与x的函数图象大致为( )
A B C D
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若反比例函数y=的图象经过点(1,-3),则k的值为 .
12.已知△ABC∽A'B'C,AB=2,A'B'=6,则△ABC与△A'B'C的周长之比为 .
13.如图,在平面直角坐标系中,反比例函数y=(x>0)的图象与矩形OABC的边
AB交于点E,且AE:EB=1:2,则矩形OABC的面积为 .
14.已知二次函数y=-x2+(m-1)x+m(m为常数)。
(1)该函数图象与x轴交点的个数是 .
(2)当一2≤m≤4时,该函数图象的顶点纵坐标y?的取值范围是 .
三、(本大题共2小题,每小题8分,满分16分)
15. 如图,D是△ABC的边AB上的一点,BD=4,AB=9,BC=6.求证:△BCD∽△BAC.
16.小明要把一篇文章录人电脑,所需时间y(分)与录入文字的速度x(字/分)之间的反比例函数关系如图所示。
(1)这篇文章共有 个字,y 与x的函数表达式为 .
(2)若小明7点30分开始录入,预计完成时间不超过7点42分,请结合雨数的性质,求小明录人文字速度的最小值。
四、(本大题共2小题,每小题8分,满分16分)
17.若,a+b+c=27,求a的值。
18.如图,二次函数y=x2-x-2的图象与x轴交于A,B两点(点A在点B的左侧).
(1)若P(-2,m)为二次函数y=x2-x- 2的图象上-点,求m的值; (2)求AB的长.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在△ABC中,AB=AC=10,BC=6,点P从点B出发以1个单位/秒的速度向点A运动,同时点Q从点C出发以2个单位/秒的速度向点B运动,当一点到达终点后,另一点也停止运动。求当运动时间为多少秒时,以B、P、Q为顶点的三角形与△ABC相似?
20.如图,反比例函数为y1=上的图象与一次函数y2=x+b的图象交于A、B两点,其中A点坐标为(1,3),B点的横坐标为-3.
(1)k= , b= .
(2)观察图象可知,当y1< y2时,自变量x的取值范围为 .
(3)一次函数的图象与y轴交于点C,点P是反比例函数图象上的一个动点,若SΔOCP=6,求此时P点的坐标。
六、(本题满分12分)
21.某水果店购进某品种榴莲,榴莲的保质期为30天,平均每颗榴莲的售价为100元,由于榴莲需要冷藏保存,
因此成本也会逐日增加,第x天时,每颗榴莲的成本为y元,y与x的函数关系如图所示。
该榴莲每天的销售量为m颗,m与x之间的关系如下表所示:
第x天 1≤x≤16 16<x≤30
每天的销售量m/颗 15 x+10
(1)求y与x的函数表达.
(2)若每天的销售利润为W元,求w与x的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是
多少元?
七、(本题满分12分)
22.已知抛物线y=ax2+bx-3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,连接BC.
(1)填空:a= ,b= .
(2)如图,若D为直线BC下方抛物线上一动点(不与点C,B 重合),连接OD交BC于点E,求的最大值.
八、(本题满分14分)
23.如图,已知E、F分别为正方形ABCD边CD、AD的中点,BE,CF交于点P。
(1)求证:△DFC≌ΔCEB; (2)求证:BC2=BP?BE; (3)猜想AP与AB是否相等,并给出证明.
合肥市高新区四校2020-2021第一学期九年级期中数学试卷答案
1 2 3 4 5 6 7 8 9 10
B A D B A C D B A C
11、 -1; 12、 1:3; 13、 6; 14、 (1) 1或2; (2) 0≤y?≤
15、∵BD=4,AB=9;∴AD=5,BD:BC=4:6=2:3,BC:AB=6:9=2:3,∴BD:BC= BC:AB,
又∠B=∠B,∴△BCD∽△BAC;
16、(1)1500; ; (2)速度最小值为125字/分;
17、 6; 18、(1)4; (2)3; 19、或;
20、(1)k=3; b=2; (2)x>1或-3<x<0; (3)P(6,)或(-6,)
21、(1)y=x+60; (2)第17天利润最大,最大为621元;
22、(1)a=1; b=-2; (2);
23、(1)∵E、F分别为正方形ABCD边CD、AD的中点,∴BC=CD,CE=DF,∠BCE=∠CDF;∴△DFC≌ΔCEB;
(2)由(1)△DFC≌ΔCEB;∴∠CBE=∠DCF;∴∠CBF+∠BCP=90°,即∠BPC=90°,∴∠BPC=∠BCE;
∠CBP=∠EBC;∴△PBC∽ΔCBE;∴BP:BC=BC:BE,即BC2=BP?BE;
(3)过点A作AG⊥BP,垂足为G,设正方形ABCD边长为2a;由(1)得FC=BE=a;同时∠AGB=∠CDF=90°,
∠ABG=∠CFD;∴△AGB∽ΔCDF;∴BG:DF=AB:FC,即BG:a=2a:a,∴BG=a;
又:∠CPE=∠CDF=90°,∠ECP=∠FCD;∴△PCE∽ΔDCF;∴EP:DF=CE:FC,即BG:a=a:a,∴EP=a;
∴PG=BE-EP-BG=a=BG;则AG为线段BP的垂直平分线,即AP=AB。
同课章节目录
