垂径定理1

(共22张PPT)
24.1.2垂径定理
问题 ：你知道赵州桥吗 它是1300多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶．它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m，你能求出赵洲桥主桥拱的半径吗？
赵州桥主桥拱的半径是多少？
·
O
C
D
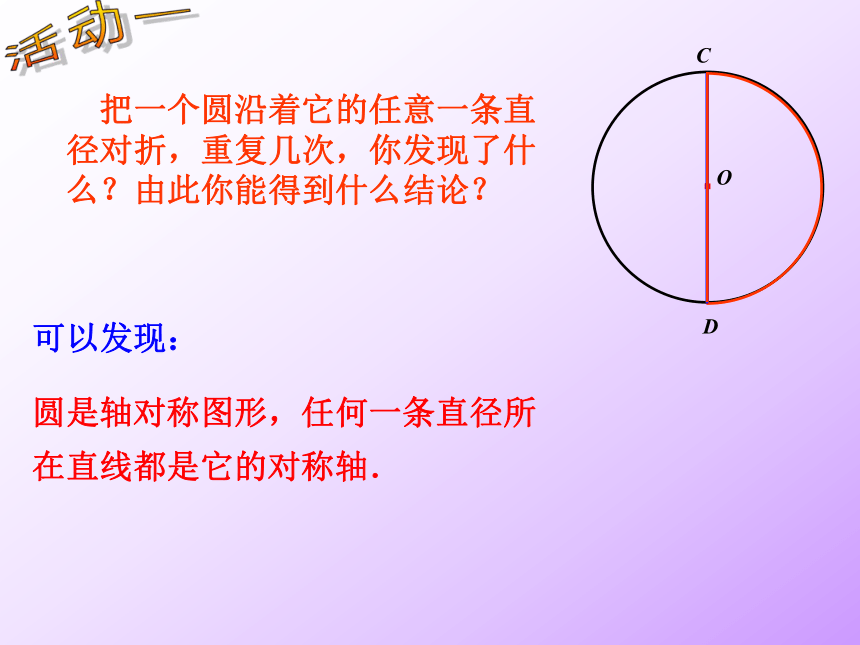
　把一个圆沿着它的任意一条直径对折，重复几次，你发现了什么？由此你能得到什么结论？
可以发现：
圆是轴对称图形，任何一条直径所在直线都是它的对称轴．　
如图，AB是⊙O的一条弦，做直径CD，使CD⊥AB，垂足为E．
（1）这个图形是轴对称图形吗？如果是，它的对称轴是什么？
（2）你能发现图中有那些相等的线段和弧？为什么？
·
O
A
B
C
D
E
活 动 二
（1）是轴对称图形．直径CD所在的直线是它的对称轴
（2） 线段： AE=BE
⌒
⌒
弧：ＡＣ＝ＢＣ　，ＡＤ＝ＢＤ
⌒
⌒
把圆沿着直径CD折叠时，CD两侧的两个半圆重合，　
点A与点B重合，AE与BE重合，ＡＣ　和　ＢＣ　
重合，ＡＤ和　ＢＤ重合．
⌒
⌒
⌒
⌒
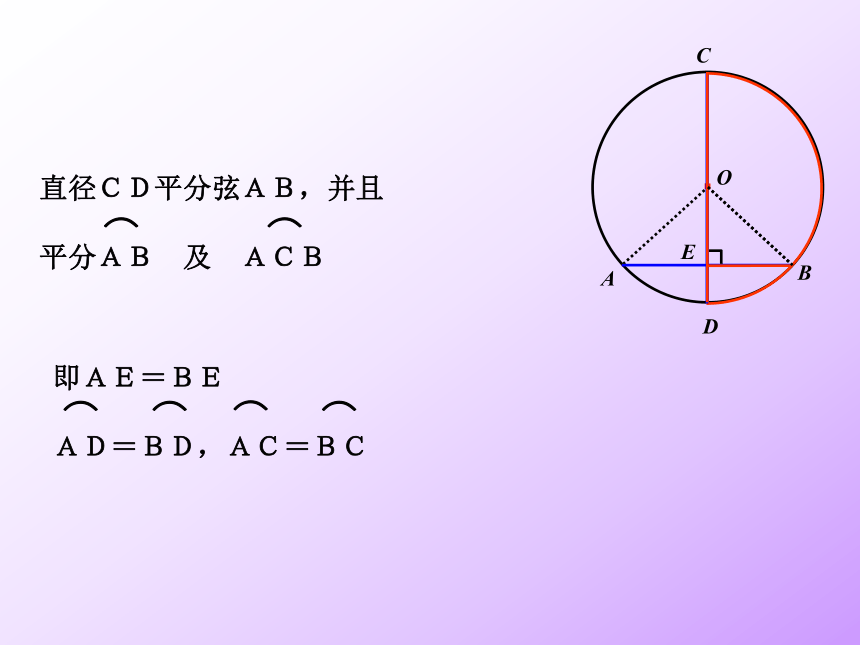
直径ＣＤ平分弦ＡＢ，并且
平分ＡＢ　及　ＡＣＢ
⌒
⌒
·
O
A
B
C
D
E
即ＡＥ＝ＢＥ　
ＡＤ＝ＢＤ，ＡＣ＝ＢＣ
⌒
⌒
⌒
⌒
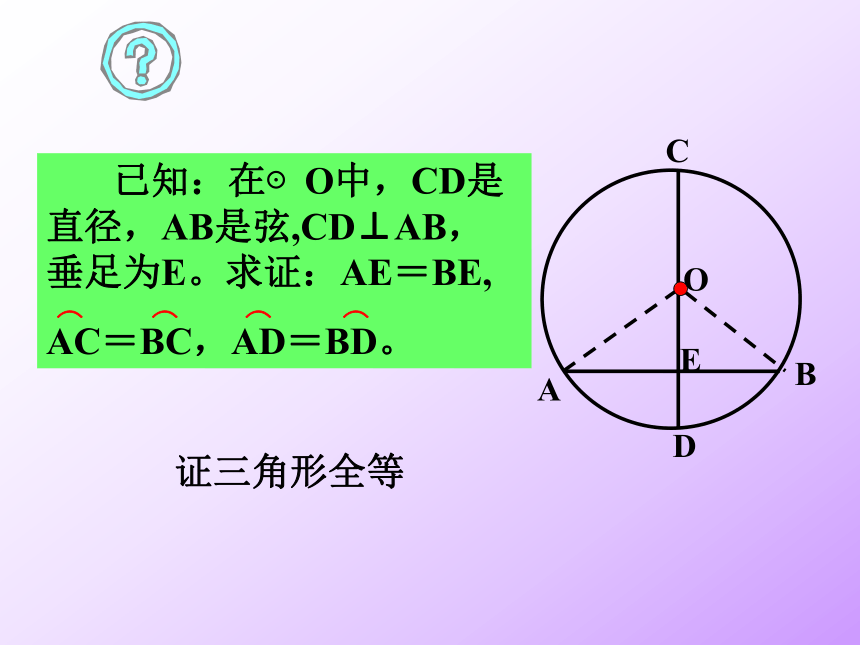
已知：在⊙O中，CD是直径，AB是弦,CD⊥AB，垂足为E。求证：AE＝BE,
AC＝BC，AD＝BD。
⌒
⌒
⌒
⌒
C
O
A
E
B
D
证三角形全等
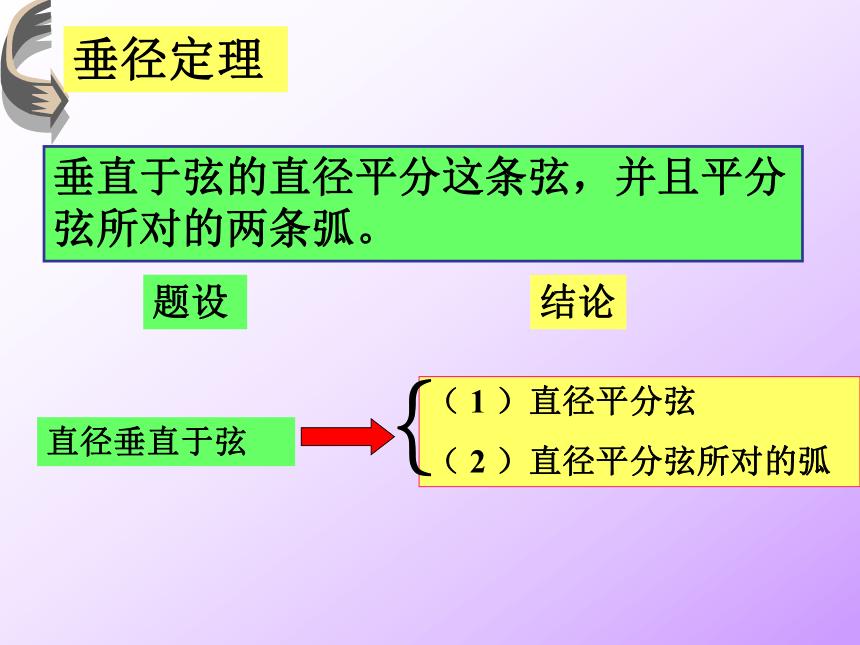
垂径定理
垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。
题设
结论
直径垂直于弦
（ 1 ）直径平分弦
（ 2 ）直径平分弦所对的弧
｛
③AE=BE,
由 ① CD是直径
② CD⊥AB
可推得
⌒
⌒
⑤AD=BD.
⌒
⌒
④AC=BC,
垂径定理：
判断下列图形，能否使用垂径定理？
注意：定理中的两个条件（直径，垂直于弦）缺一不可！
Ramming foundation
如图在⊙O中，CD是直径，AB是弦, AE＝BE
则：CD⊥AB,
AC＝BC，AD＝BD吗
⌒
⌒
⌒
⌒
C
O
A
E
B
D
想一想
平分弦 (不是直径) 的直径垂直于弦,并且平分弦所对的两条弧。
题设
结论
直径平分弦
(不是直径)
（ 1 ）直径垂直于弦
（ 2 ）直径平分弦所对的弧
｛
②CD⊥AB,
由 ① CD是直径
③ AM=BM
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
可推得
推论：
问题 ：你知道赵州桥吗 它是1300多年前我国隋代建造的石拱桥, 是我国古代人民勤劳与智慧的结晶．它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m，你能求出赵洲桥主桥拱的半径吗？
解得：R≈27．9（m）
B
O
D
A
C
R
解决求赵州桥拱半径的问题
在Rt△OAD中，由勾股定理，得
即 R2=18.72+（R－7.2）2
∴赵州桥的主桥拱半径约为27.9m.
OA2=AD2+OD2
AB=37.4，CD=7.2，
OD=OC－CD=R－7.2
在图中
如图，用 ＡＢ 表示主桥拱，设 ＡＢ所在圆的圆心为O，半径为R．经过圆心O 作弦AB 的垂线OC，D为垂足，OC与AB 相交于点D，根据前面的结论，D 是AB 的中点，C是ＡＢ 的中点，CD 就是拱高．
⌒
⌒
⌒
解：
学会作辅助线
如图，P为⊙O的弦BA延长线上一点，PA＝AB＝2，PO＝5，求⊙O的半径。
关于弦的问题，常常需要过圆心作弦的垂线段，这是一条非常重要的辅助线。
圆心到弦的距离、半径、弦长构成直角三角形，便将问题转化为直角三角形的问题。
Ramming foundation
C
我成功，我快乐
变式1：AC、BD有什么关系？
O
A
B
C
D
变式2：AC＝BD依然成立吗？
变式3：EA＝____, EC=_____。
变式4：______ AC=BD.
变式5：______ AC=BD.
Ramming foundation
1．如图，在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，求⊙O的半径．
·
O
A
B
E
练习
解：
答：⊙O的半径为5cm.
在Rt △ AOE 中
2．如图，在⊙O中，AB、AC为互相垂直且相等的两条弦，OD⊥AB于D，OE⊥AC于E，求证四边形ADOE是正方形．
D
·
O
A
B
C
E
证明：
∴四边形ADOE为矩形，
又　∵AC=AB
∴ AE=AD
∴ 四边形ADOE为正方形.
不学自知,不问自晓,古今行事,未之有也.
努力吧同学们！