人教版数学九年级上册 24.2.2 直线和圆的位置关系课件(共25张PPT)
文档属性
| 名称 | 人教版数学九年级上册 24.2.2 直线和圆的位置关系课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 168.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-01 16:34:04 | ||
图片预览





文档简介
(共25张PPT)
圆的切线的判定
复
习
1.直线和圆有哪些位置关系?
2.如何判断直线与圆相切?有几种方法?
判定直线与圆相切的方法
1.看直线与圆交点的个数(有且只有一个)。
2.比较圆心到直线的距离与半径的大小。(d=r)
那么是否还有其他方法呢?
.
O
A
L
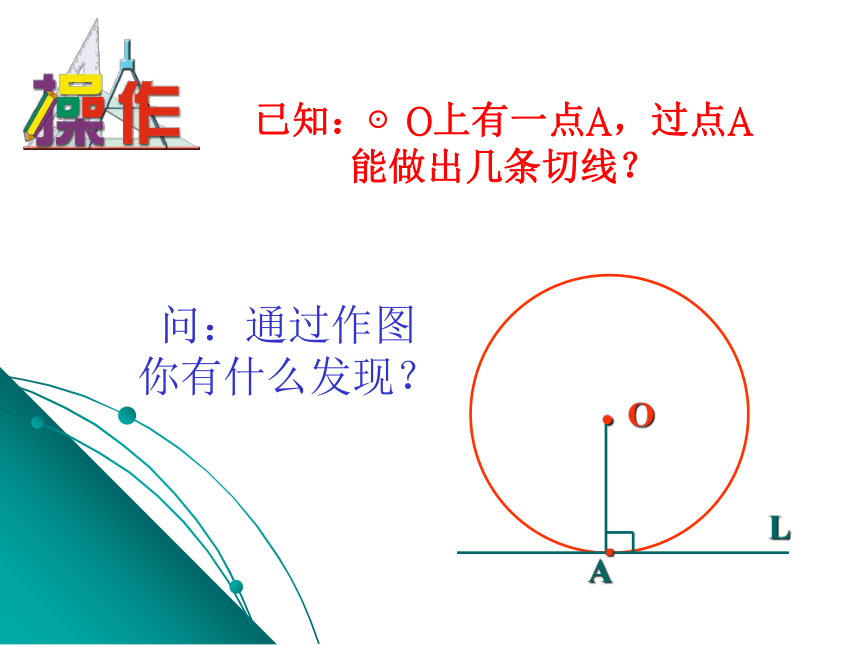
已知:⊙O上有一点A,过点A能做出几条切线?
.
问:通过作图你有什么发现?
.
O
A
L
经过半径的外端点并且垂直于这条半径的直线是圆的切线.
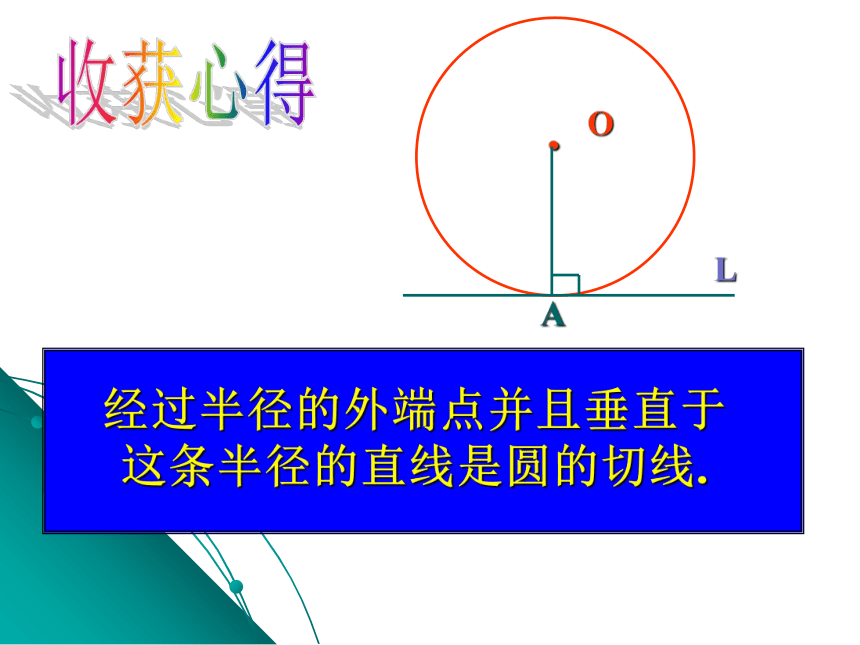
收获心得
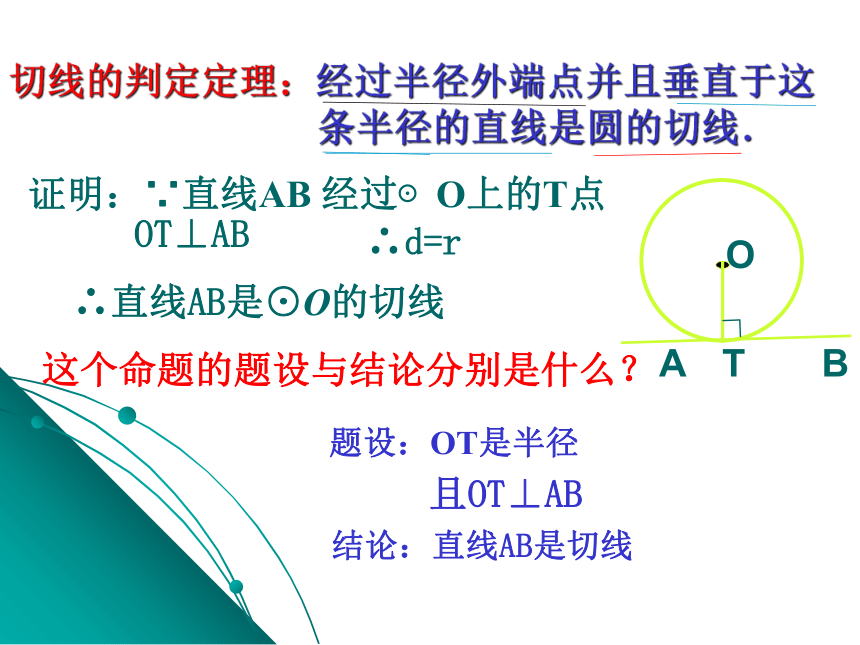
切线的判定定理:经过半径外端点并且垂直于这
条半径的直线是圆的切线.
∟
T
B
A
O
证明:∵直线AB
经过⊙O上的T点
OT⊥AB
∴直线AB是⊙O的切线
这个命题的题设与结论分别是什么?
题设:OT是半径
且OT⊥AB
结论:直线AB是切线
∴d=r
归纳:
O
r
l
A
文字叙述:
经过半径的外端并且垂直于这
条半径的直线是圆的切线。
∵
OA是半径,OA⊥l于A
∴
l是⊙O的切线。
几何语言:
切线的判定定理
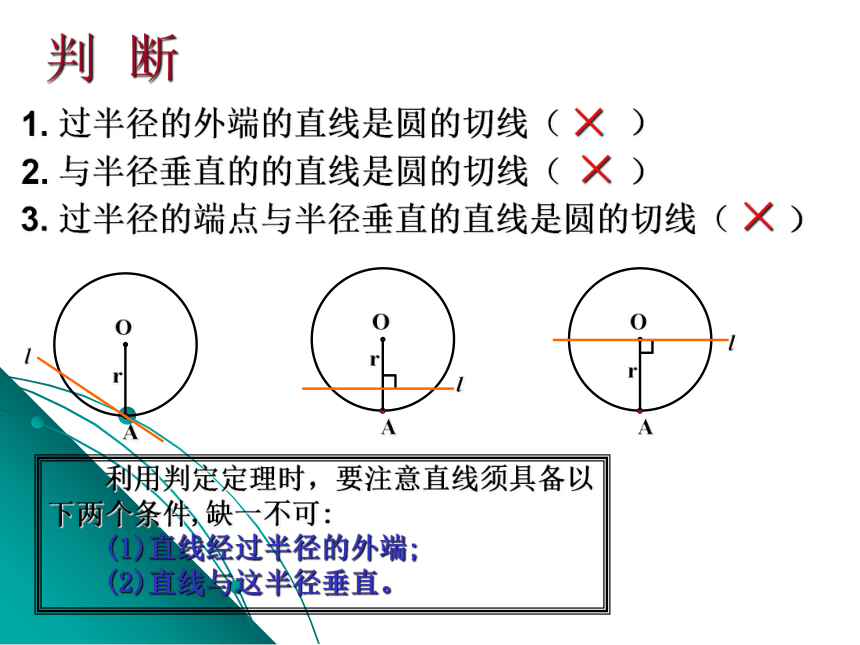
判
断
1.
过半径的外端的直线是圆的切线(
)
2.
与半径垂直的的直线是圆的切线(
)
3.
过半径的端点与半径垂直的直线是圆的切线(
)
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
利用判定定理时,要注意直线须具备以下两个条件,缺一不可:
(1)直线经过半径的外端;
(2)直线与这半径垂直。
判断一条直线是圆的切线,你现在会有多少种方法?
切线判定有以下三种方法:
1.利用切线的定义:与圆有唯一公共点的直线是圆的切线。
2.利用d与r的关系作判断:当d=r时直线是圆的切线。
3.利用切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
想一想
〖例1〗
已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
O
B
A
C
分析:由于AB过⊙O上的点C,所以连接OC,只要证明
AB⊥OC即可。
证明:连结OC(如图)。
∵
OA=OB,CA=CB,
∴
AB⊥OC(三线合一)
又
∵
OC是⊙O的半径
∴
AB是⊙O的切线。
〖例2〗
已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为
半径作⊙O。
求证:⊙O与AC相切。
O
A
B
C
E
D
证明:过O作OE⊥AC于E。
∵
AO平分∠BAC,OD⊥AB
OD⊥AB于点D
∴
OE=OD
∵
OD是⊙O的半径
∴
OE也是半径
又
∵
OE⊥AC
∴
AC是⊙O的切线。
小
结
例1与例2的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。简记为:有交点,连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。简记为:无交点,作垂直,证半径。
O
B
A
C
O
A
B
C
E
D
练
习
1.如图,△AOB中,OA=OB=10,∠AOB=120°,以O为圆心,
5为半径的⊙O与OA、OB相交。
求证:AB是⊙O的切线。
O
B
A
C
2、如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P,PE⊥AC于E。
求证:PE是⊙O的切线
B
C
O
A
E
P
证明:连结OP。
∵AB=AC,∴∠B=∠C。
∵OB=OP,∴∠B=∠OPB,
∴∠OBP=∠C。
∴OP∥AC。
∵PE⊥AC,
∴∠PEC=90°
∴
∠OPE=∠PEC=90°
∴PE⊥OP。
∴PE为⊙0的切线。
2、如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P,PE⊥AC于E。
求证:PE是⊙O的切线。
练
习
B
C
O
A
E
P
拓展提高
拓展提高
y
x
O
·
C
A
B
拓展提高
y
x
O
·
C
A
B
大显身手
·
解:
①当E点运动到O点时⊙C与直线OA相切,
设此时的圆心为C1,于是有OC1=CE=-3-(-10)=7
∴CC1=3
∴t1=3÷2=1.5(秒)
y
x
C
O
C1
·
A
B
大显身手
·
C2
·
O
A
B
P
x
y
大显身手
·
③设当C运动到C3时圆与直线OA相切于O点,于是有OC3=7
∴C3(7,0)
∴C3C=7-(-10)=17
t3=17÷2=8.5(秒)
O
A
B
C3
·
C2
·
x
y
大显身手
·
③设当C运动到C4时圆与直线AB相切于Q点,
连C4
Q,则C4
Q⊥AB
∠C4
BQ=30°
∴
B
C4
=2
C4
Q=14
∴
CC4
=10+12+14=36
∴
t4=36÷2=18(秒)
O
A
B
C4
x
C3
y
Q
你有收获吗?加油!
心得体会
1、判定切线的方法有哪些?
(1)直线与圆的公共点已知时,作出过公共点的半径,再证半径垂直
于该直线。(连半径,证垂直)
(2)直线与圆的公共点不确定时,过圆心作直线的垂线段,再证明这
条垂线段为圆的半径。(作垂直,证半径)
与圆有唯一公共点
是圆的切线
直线l与圆心的距离等于圆的半径
经过半径外端且垂直这条半径
是圆的切线
是圆的切线
2、常用的添辅助线方法?
作业布置:同步相应练习
补充作业:如图,直线y=-
x+4与y轴交于点A,与x轴交于
点B,以点C(
,0)为圆心,OC的长为半径作⊙C,
证明:AB是⊙C的切线。
M
分析:由于不知AB和⊙C是否有公共点,故考虑过C作CM⊥AB于M,再证CM为⊙C的半径即可
证明:过C点作CM⊥AB于M点,
∵直线y=-
x+4交x轴、y轴于B、A点
∴A的坐标为(0,4),B的坐标为(3,0)
∴OA=4,OB=3,BC=3-
=
又由勾股定理可知
AB=
=
=5
由S△ABC=
AB·CM=
BC·AO得
∴
×5·CM=
×
×4
∴CM=
∴CM=OC
又CM⊥AB
故AB为⊙C的切线
M
圆的切线的判定
复
习
1.直线和圆有哪些位置关系?
2.如何判断直线与圆相切?有几种方法?
判定直线与圆相切的方法
1.看直线与圆交点的个数(有且只有一个)。
2.比较圆心到直线的距离与半径的大小。(d=r)
那么是否还有其他方法呢?
.
O
A
L
已知:⊙O上有一点A,过点A能做出几条切线?
.
问:通过作图你有什么发现?
.
O
A
L
经过半径的外端点并且垂直于这条半径的直线是圆的切线.
收获心得
切线的判定定理:经过半径外端点并且垂直于这
条半径的直线是圆的切线.
∟
T
B
A
O
证明:∵直线AB
经过⊙O上的T点
OT⊥AB
∴直线AB是⊙O的切线
这个命题的题设与结论分别是什么?
题设:OT是半径
且OT⊥AB
结论:直线AB是切线
∴d=r
归纳:
O
r
l
A
文字叙述:
经过半径的外端并且垂直于这
条半径的直线是圆的切线。
∵
OA是半径,OA⊥l于A
∴
l是⊙O的切线。
几何语言:
切线的判定定理
判
断
1.
过半径的外端的直线是圆的切线(
)
2.
与半径垂直的的直线是圆的切线(
)
3.
过半径的端点与半径垂直的直线是圆的切线(
)
×
×
×
O
r
l
A
O
r
l
A
O
r
l
A
利用判定定理时,要注意直线须具备以下两个条件,缺一不可:
(1)直线经过半径的外端;
(2)直线与这半径垂直。
判断一条直线是圆的切线,你现在会有多少种方法?
切线判定有以下三种方法:
1.利用切线的定义:与圆有唯一公共点的直线是圆的切线。
2.利用d与r的关系作判断:当d=r时直线是圆的切线。
3.利用切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
想一想
〖例1〗
已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。
O
B
A
C
分析:由于AB过⊙O上的点C,所以连接OC,只要证明
AB⊥OC即可。
证明:连结OC(如图)。
∵
OA=OB,CA=CB,
∴
AB⊥OC(三线合一)
又
∵
OC是⊙O的半径
∴
AB是⊙O的切线。
〖例2〗
已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为
半径作⊙O。
求证:⊙O与AC相切。
O
A
B
C
E
D
证明:过O作OE⊥AC于E。
∵
AO平分∠BAC,OD⊥AB
OD⊥AB于点D
∴
OE=OD
∵
OD是⊙O的半径
∴
OE也是半径
又
∵
OE⊥AC
∴
AC是⊙O的切线。
小
结
例1与例2的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。简记为:有交点,连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。简记为:无交点,作垂直,证半径。
O
B
A
C
O
A
B
C
E
D
练
习
1.如图,△AOB中,OA=OB=10,∠AOB=120°,以O为圆心,
5为半径的⊙O与OA、OB相交。
求证:AB是⊙O的切线。
O
B
A
C
2、如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P,PE⊥AC于E。
求证:PE是⊙O的切线
B
C
O
A
E
P
证明:连结OP。
∵AB=AC,∴∠B=∠C。
∵OB=OP,∴∠B=∠OPB,
∴∠OBP=∠C。
∴OP∥AC。
∵PE⊥AC,
∴∠PEC=90°
∴
∠OPE=∠PEC=90°
∴PE⊥OP。
∴PE为⊙0的切线。
2、如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P,PE⊥AC于E。
求证:PE是⊙O的切线。
练
习
B
C
O
A
E
P
拓展提高
拓展提高
y
x
O
·
C
A
B
拓展提高
y
x
O
·
C
A
B
大显身手
·
解:
①当E点运动到O点时⊙C与直线OA相切,
设此时的圆心为C1,于是有OC1=CE=-3-(-10)=7
∴CC1=3
∴t1=3÷2=1.5(秒)
y
x
C
O
C1
·
A
B
大显身手
·
C2
·
O
A
B
P
x
y
大显身手
·
③设当C运动到C3时圆与直线OA相切于O点,于是有OC3=7
∴C3(7,0)
∴C3C=7-(-10)=17
t3=17÷2=8.5(秒)
O
A
B
C3
·
C2
·
x
y
大显身手
·
③设当C运动到C4时圆与直线AB相切于Q点,
连C4
Q,则C4
Q⊥AB
∠C4
BQ=30°
∴
B
C4
=2
C4
Q=14
∴
CC4
=10+12+14=36
∴
t4=36÷2=18(秒)
O
A
B
C4
x
C3
y
Q
你有收获吗?加油!
心得体会
1、判定切线的方法有哪些?
(1)直线与圆的公共点已知时,作出过公共点的半径,再证半径垂直
于该直线。(连半径,证垂直)
(2)直线与圆的公共点不确定时,过圆心作直线的垂线段,再证明这
条垂线段为圆的半径。(作垂直,证半径)
与圆有唯一公共点
是圆的切线
直线l与圆心的距离等于圆的半径
经过半径外端且垂直这条半径
是圆的切线
是圆的切线
2、常用的添辅助线方法?
作业布置:同步相应练习
补充作业:如图,直线y=-
x+4与y轴交于点A,与x轴交于
点B,以点C(
,0)为圆心,OC的长为半径作⊙C,
证明:AB是⊙C的切线。
M
分析:由于不知AB和⊙C是否有公共点,故考虑过C作CM⊥AB于M,再证CM为⊙C的半径即可
证明:过C点作CM⊥AB于M点,
∵直线y=-
x+4交x轴、y轴于B、A点
∴A的坐标为(0,4),B的坐标为(3,0)
∴OA=4,OB=3,BC=3-
=
又由勾股定理可知
AB=
=
=5
由S△ABC=
AB·CM=
BC·AO得
∴
×5·CM=
×
×4
∴CM=
∴CM=OC
又CM⊥AB
故AB为⊙C的切线
M
同课章节目录
