冀教版初中数学九年级上册:25.5 相似三角形的性质 课件(17张PPT)
文档属性
| 名称 | 冀教版初中数学九年级上册:25.5 相似三角形的性质 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 482.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-01 17:30:19 | ||
图片预览


文档简介
(共17张PPT)
相似三角形的性质
25.5
问题情境
A
B
C
H
G
D
F
E
K
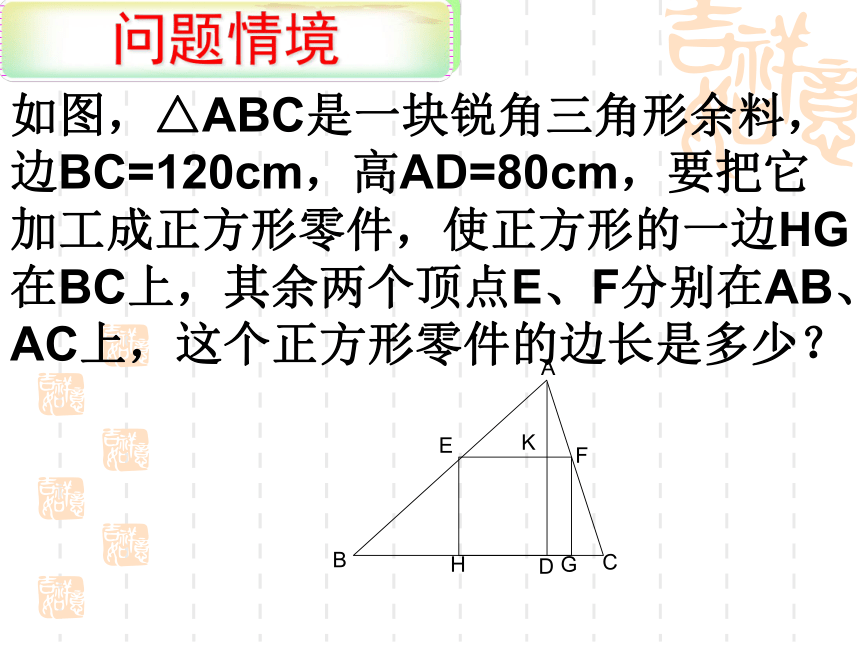
如图,△ABC是一块锐角三角形余料,边BC=120cm,高AD=80cm,要把它加工成正方形零件,使正方形的一边HG在BC上,其余两个顶点E、F分别在AB、AC上,这个正方形零件的边长是多少?
知识链接
1、若△ABC∽△DEF,∠A=50°,∠E=60°,则∠C=
2、如图,在△ABC中,DE∥BC,若AD:DB=1:3,则△ADE与△ABC的相似比为
3、已知:△ABC△∽ABC,AB=3cm,BC=4cm,A′B′=6cm,A′C′=4cm,则AC=
cm
,
B′C′=
cm。
4、
D
A
B
C
E
3
4
B
A
C
6
8
A′
B′
C′
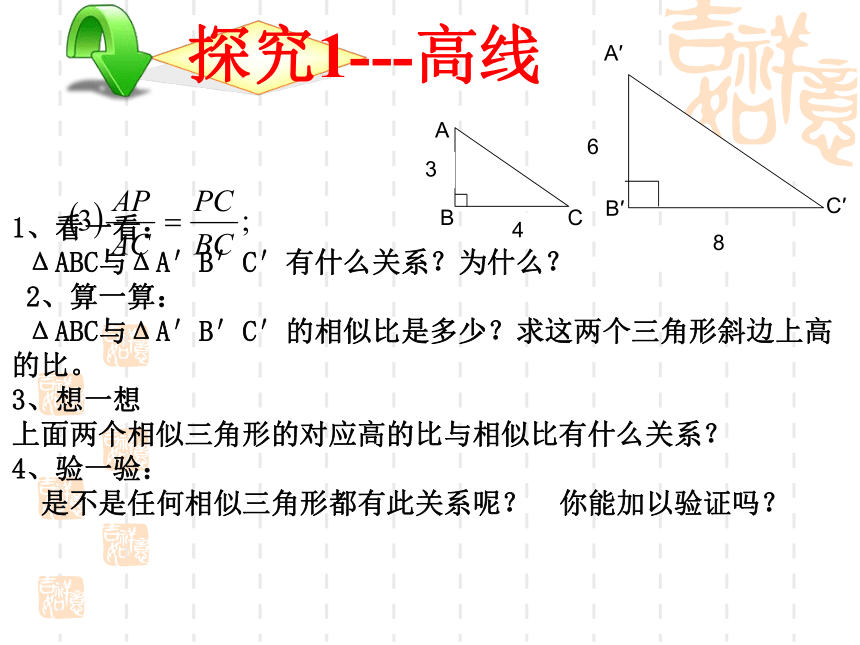
1、看一看:
ΔABC与ΔA′B′C′有什么关系?为什么?
2、算一算:
ΔABC与ΔA′B′C′的相似比是多少?求这两个三角形斜边上高的比。
3、想一想
上面两个相似三角形的对应高的比与相似比有什么关系?
4、验一验:
是不是任何相似三角形都有此关系呢?
你能加以验证吗?
探究1---高线
探究1---高线
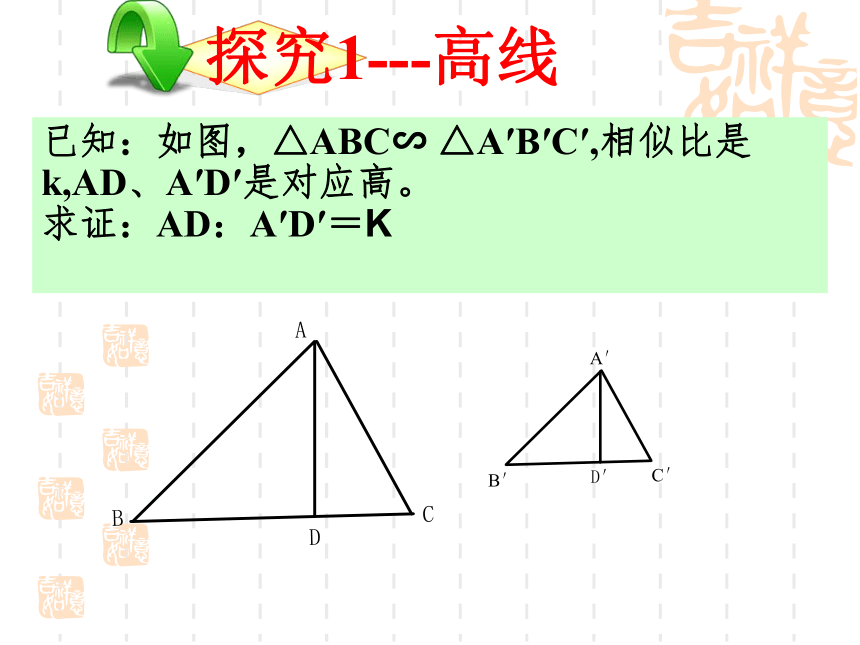
已知:如图,△ABC∽
△A′B′C′,相似比是k,AD、A′D′是对应高。
求证:AD:A′D′=K
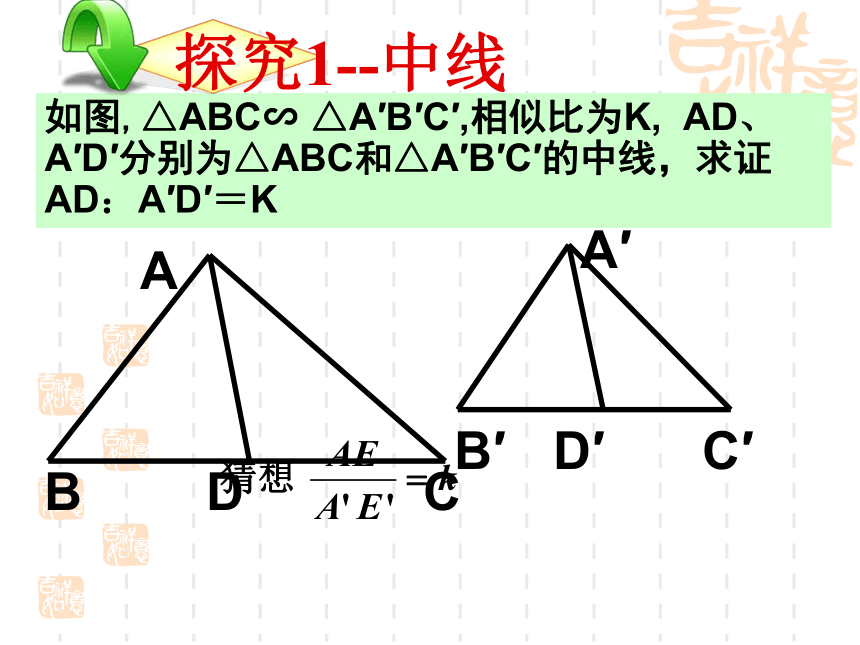
如图,△ABC∽
△A′B′C′,相似比为K,
AD、A′D′分别为△ABC和△A′B′C′的中线,求证
AD:A′D′=K
探究1--中线
C′
A
B
C
D
A′
B′
D′
如图,△ABC∽
△A′B′C′,相似比为K,
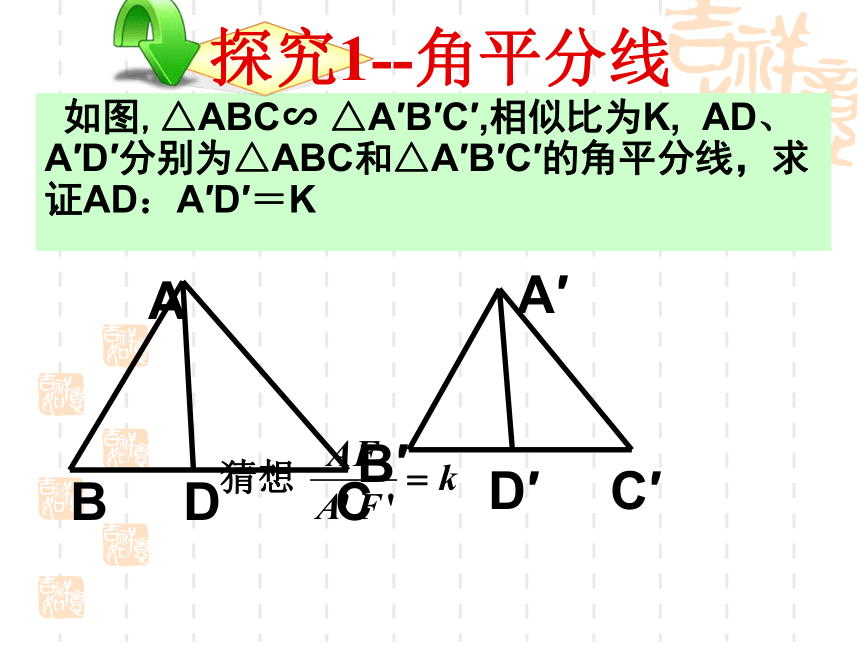
AD、A′D′分别为△ABC和△A′B′C′的角平分线,求证AD:A′D′=K
探究1--角平分线
A
B
C
D
A′
C′
D′
B′
1、若两个相似三角形的相似比是2∶3,则它们的对应高线的比是
___
,对应中线的比是
___
,对应角平分线的比是
___
.
2、顺次连接三角形三边的中点,所围成的三角形与原三角形的对应中线的比是___
,对应角平分线的比是___
.
3、已知△ABC∽△A?B?C?,AD、A
?D
?分别是对应边BC、B
?C
?上的高,若BC=8cm,B
?C
?=6cm,AD=4cm,则A
?D
?等于(
)
A
16cm
B
12
cm
C
3
cm
D
6
cm
成果展示1
如图,4
×4正方形网格
1、看一看:
ΔABC与ΔA′B′C′有什么关系?为什么?
2、算一算:
ΔABC与ΔA′B′C′的相似比是多少?
ΔABC与ΔA′B′C′的周长比是多少?
面积比是多少?
3、想一想:
上面两个相似三角形的周长比与相似比有什么关系?面积比与相似比又有什么关系?
4、验一验:
是不是任何相似三角形都有此关系呢?
你能加以验证吗?
探究2--周长、面积
探究2--周长
如图,△ABC∽△A'B'C'
,相似比为k,
求它们周长的比.
∵△ABC∽△A'B'C'
A'
B'
C'
A
B
C
如图,△ABC∽△A1B1C1,相似比为k,它们面积的比与相似比有什么关系?
探究2--面积
?
A1
B1
C1
A
B
C
∵
∴
D
D1
S△ABC
S△A1B1C1
=
=k·k=
k2
如图,分别作△ABC和△
A1B1C1的
对应高AD和A1D1.
成果展示2
1、把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的___倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来___倍。
2、若△ABC∽△A′B′C′,且,△ABC的周长为12cm,则△A′B′C′的周长为___
3题图
4题图
3、如图,D、E分别是△ABC的边AB、AC上的点,
则△AED与△ABC的面积比是________。
4、如图,在梯形ABCD中,AD//BC,AC,BD交于点O,
S△AOD:
S△BOC=1:2,那么AD:BC=________。
6、西安大唐芙蓉园占地面积约为800000m2,若按比例尺1:2000缩小后,其面积大约相当于(
)
A
、
一个篮球场的面积
B
、一张乒乓球台台面的面积
C
、
《陕西日报》的一个版面的面积
D、《数学》课本封面的面积
A
B
C
D
E
如图,△ABC是一块锐角三角形余料,边BC=120厘米,高AD=80厘米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
E
G
B
F
H
K
D
C
A
精讲释疑
能力提升
变式(一)已知:如图,在△ABC中,AD是高,矩形EFGH内接于△ABC,且长边FG在BC上,矩形相邻两边EF:FG=1:2,若BC=30㎝,AD=10㎝,求矩形EFGH的面积。
变式(二)如图,已知△ABC的面积是12,BC=6,点E、I分别在边AB、AC上,在BC边上依次做了n个全等的小正方形DEFG,GFMN,...,KHIJ,则每个小正方形的边长为(
)
A.
B.
C.
D.
能力提升
大家都来说
我学了-------
我学会了-------
我还有待加强-------
达标测试
1、已知:梯形ABCD中,AD∥BC,AD=36cm,BC=60cm,延长两腰BA,CD交于点O,OF⊥BC,交AD于E,EF=32cm,则OF=_______.
1题
2题
3题
4题
2、如图:D是△ABC的边AB上一点,过D作DE∥BC交AC于E,已知AD:BD=3:2,则S△ABC
:S四边形BCED=
3、如图,在△ABC中,DE//BC,若AE:EC=1:2,△DOE与△BOC的周长比为______面积比为______。
4.如图,把△ABC沿AB边平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC的面积的一半,若AB=2,则此三角形移动的距离BE的长为______。
D
A
B
C
E
相似三角形的性质
25.5
问题情境
A
B
C
H
G
D
F
E
K
如图,△ABC是一块锐角三角形余料,边BC=120cm,高AD=80cm,要把它加工成正方形零件,使正方形的一边HG在BC上,其余两个顶点E、F分别在AB、AC上,这个正方形零件的边长是多少?
知识链接
1、若△ABC∽△DEF,∠A=50°,∠E=60°,则∠C=
2、如图,在△ABC中,DE∥BC,若AD:DB=1:3,则△ADE与△ABC的相似比为
3、已知:△ABC△∽ABC,AB=3cm,BC=4cm,A′B′=6cm,A′C′=4cm,则AC=
cm
,
B′C′=
cm。
4、
D
A
B
C
E
3
4
B
A
C
6
8
A′
B′
C′
1、看一看:
ΔABC与ΔA′B′C′有什么关系?为什么?
2、算一算:
ΔABC与ΔA′B′C′的相似比是多少?求这两个三角形斜边上高的比。
3、想一想
上面两个相似三角形的对应高的比与相似比有什么关系?
4、验一验:
是不是任何相似三角形都有此关系呢?
你能加以验证吗?
探究1---高线
探究1---高线
已知:如图,△ABC∽
△A′B′C′,相似比是k,AD、A′D′是对应高。
求证:AD:A′D′=K
如图,△ABC∽
△A′B′C′,相似比为K,
AD、A′D′分别为△ABC和△A′B′C′的中线,求证
AD:A′D′=K
探究1--中线
C′
A
B
C
D
A′
B′
D′
如图,△ABC∽
△A′B′C′,相似比为K,
AD、A′D′分别为△ABC和△A′B′C′的角平分线,求证AD:A′D′=K
探究1--角平分线
A
B
C
D
A′
C′
D′
B′
1、若两个相似三角形的相似比是2∶3,则它们的对应高线的比是
___
,对应中线的比是
___
,对应角平分线的比是
___
.
2、顺次连接三角形三边的中点,所围成的三角形与原三角形的对应中线的比是___
,对应角平分线的比是___
.
3、已知△ABC∽△A?B?C?,AD、A
?D
?分别是对应边BC、B
?C
?上的高,若BC=8cm,B
?C
?=6cm,AD=4cm,则A
?D
?等于(
)
A
16cm
B
12
cm
C
3
cm
D
6
cm
成果展示1
如图,4
×4正方形网格
1、看一看:
ΔABC与ΔA′B′C′有什么关系?为什么?
2、算一算:
ΔABC与ΔA′B′C′的相似比是多少?
ΔABC与ΔA′B′C′的周长比是多少?
面积比是多少?
3、想一想:
上面两个相似三角形的周长比与相似比有什么关系?面积比与相似比又有什么关系?
4、验一验:
是不是任何相似三角形都有此关系呢?
你能加以验证吗?
探究2--周长、面积
探究2--周长
如图,△ABC∽△A'B'C'
,相似比为k,
求它们周长的比.
∵△ABC∽△A'B'C'
A'
B'
C'
A
B
C
如图,△ABC∽△A1B1C1,相似比为k,它们面积的比与相似比有什么关系?
探究2--面积
?
A1
B1
C1
A
B
C
∵
∴
D
D1
S△ABC
S△A1B1C1
=
=k·k=
k2
如图,分别作△ABC和△
A1B1C1的
对应高AD和A1D1.
成果展示2
1、把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的___倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来___倍。
2、若△ABC∽△A′B′C′,且,△ABC的周长为12cm,则△A′B′C′的周长为___
3题图
4题图
3、如图,D、E分别是△ABC的边AB、AC上的点,
则△AED与△ABC的面积比是________。
4、如图,在梯形ABCD中,AD//BC,AC,BD交于点O,
S△AOD:
S△BOC=1:2,那么AD:BC=________。
6、西安大唐芙蓉园占地面积约为800000m2,若按比例尺1:2000缩小后,其面积大约相当于(
)
A
、
一个篮球场的面积
B
、一张乒乓球台台面的面积
C
、
《陕西日报》的一个版面的面积
D、《数学》课本封面的面积
A
B
C
D
E
如图,△ABC是一块锐角三角形余料,边BC=120厘米,高AD=80厘米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
E
G
B
F
H
K
D
C
A
精讲释疑
能力提升
变式(一)已知:如图,在△ABC中,AD是高,矩形EFGH内接于△ABC,且长边FG在BC上,矩形相邻两边EF:FG=1:2,若BC=30㎝,AD=10㎝,求矩形EFGH的面积。
变式(二)如图,已知△ABC的面积是12,BC=6,点E、I分别在边AB、AC上,在BC边上依次做了n个全等的小正方形DEFG,GFMN,...,KHIJ,则每个小正方形的边长为(
)
A.
B.
C.
D.
能力提升
大家都来说
我学了-------
我学会了-------
我还有待加强-------
达标测试
1、已知:梯形ABCD中,AD∥BC,AD=36cm,BC=60cm,延长两腰BA,CD交于点O,OF⊥BC,交AD于E,EF=32cm,则OF=_______.
1题
2题
3题
4题
2、如图:D是△ABC的边AB上一点,过D作DE∥BC交AC于E,已知AD:BD=3:2,则S△ABC
:S四边形BCED=
3、如图,在△ABC中,DE//BC,若AE:EC=1:2,△DOE与△BOC的周长比为______面积比为______。
4.如图,把△ABC沿AB边平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC的面积的一半,若AB=2,则此三角形移动的距离BE的长为______。
D
A
B
C
E
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
