2020-2021学年江西赣州高三上数学第二次月考试卷 (B卷) Word版含解析
文档属性
| 名称 | 2020-2021学年江西赣州高三上数学第二次月考试卷 (B卷) Word版含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 336.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 06:47:13 | ||
图片预览




文档简介
2020-2021学年江西赣州高三上数学月考试卷
一、选择题
?
1. 已知集合A={x|?2≤x≤2},B={x|y=lg(x?1)},则A∩B=(? ? ? ? )
A.x|x≥?2 B.x|1?
2. 已知函数f(x)=logax+a,x>1,(4?a)x+2,x≤1?是R上的单调递增函数,则a的取值范围是(? ? ? ? )
A.[3,?4) B.[2,?4) C.(1,?4) D.(1,?3]
?
3. 已知实数a,b,c满足a
A.a2?
4. 已知函数f(x)=(2x+2?x)ln|x|的图象大致为(? ? ? ? )
A. B.
C. D.
?
5. 抛物线C:y2=4x的焦点为F,点A在抛物线上,且点A到直线x=?3的距离是线段AF长度的2倍,则线段AF的长度为(? ? ? ? )
A.1 B.2 C.3 D.4
?
6. 已知a=log23, b=1212 ,c=1313,则a,b,c的大小关系是(????????)
A.a?
7. 设函数fx=x+log2x?m,则“函数fx在(12,4)上存在零点”是“m∈1,6”的(? ? ? ? )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
?
8. 已知函数fx=12x?a+12为奇函数,则a=(? ? ? ? ? ?)
A.?2 B.?1 C.0 D.1
?
9. 已知3sinα+cosα2sinα?3cosα=7,则函数fx=sin2x+2tanα|cosx|?6的最小值为(? ? ? ? )
A.?5 B.?3 C.?2 D.?1
?
10. 已知实数a,b,c满足lga=10b=1c,则下列关系式中不可能成立的是(? ? ? ? )
A.a>b>c? B.a>c>b? C.c>a>b? D.c>b>a
?
11. 设函数fx=ln4+x2+x2+1,则使得fx
A.?3,+∞ B.?∞,?3
C.?3,?1 D.?∞,?3∪?1,+∞
?
12. 已知函数y=fx在R上可导且f0=2,其导函数f′x满足,f′x?fxx?2>0,对于函数gx=fxex,下列结论错误的是(????????)
A.函数gx在2,+∞上为单调递增函数
B.x=2是函数gx的极小值点
C.x≤0时,不等式fx≤2e恒成立
D.函数gx至多有两个零点
二、填空题
?
13. 曲线y=2+lnxx在点x=1处的切线方程是________.
?
14. 设f(x)是周期为4的奇函数,当0≤x≤1时,f(x)=x?(1+x),则f(?92)=________.
?
15. 已知x>0,y>0,2x?8y=2,则1x+13y的最小值是________ .
?
16. 在三棱锥B?ACD中,BA,BC,BD两两垂直,BC=2,BD=4,三棱锥的侧面积为13,则该三棱锥外接球的表面积为________.
三、解答题
?
17. 设数列{an}的前n项和为Sn,且a1=1,an+1=2Sn+1,数列{bn}满足a1=b1,点P(bn,bn+1)在直线x?y+2=0上,n∈N*.
(1)求数列{an},{bn}的通项公式;
(2)设cn=bnan,求数列{cn}的前n项和Tn.
?
18. 已知函数fx=23sinxcosx+2cos2x?1,x∈0,π,△ABC中,角A,B,C所对的边分别为a,b,c, △ABC的面积为235a2.
(1)求函数fx的单调递减区间;
(2)若fC=1,求bc的值.
?
19. 如图,在以P为顶点的圆锥中,母线长为2,底面圆的直径AB长为2,O为圆心.C是圆O所在平面上一点,且AC与圆O相切,连接BC交圆于点D.连接PD,PC,E是PC的中点,连接OE,ED.
(1)求证:平面PBC⊥平面PAC;
(2)若二面角B?PO?D的大小为2π3,求平面PAC与平面DOE所成锐二面角的余弦值.
?
20. 已知椭圆C:x2a2+y2b2=1a>b>0的离心率为22,长轴长为42.
(1)求椭圆C的标准方程;
(2)若直线l:y=kx+mk≠0与椭圆C交于不同的两点M,N,且线段MN的垂直平分线过定点1,0,求实数k的取值范围.
?
21. 已知函数fx=exax+1.
(1)讨论函数fx的单调性;
(2)当a=1时,若P为直线y=x+3与函数fx图像的一个公共点,其横坐标为t,且t∈m,m+1,求整数m的所有可能的值.
?
22. 在平面直角坐标系xOy中,曲线C1的参数方程是x=1+3cosα,y=3sinα?(α为参数),以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρ=1.
(1)分别写出C1的极坐标方程和C2的直角坐标方程;
(2)若射线l的极坐标方程θ=π3(ρ≥0),且l分别交曲线C1,C2于A,B两点,求|AB|.
参考答案与试题解析
2020-2021学年江西赣州高三上数学月考试卷
一、选择题
1.
【答案】
C
【考点】
对数函数的定义域
交集及其运算
【解析】
化简集合B,根据交集的定义即可得解.
【解答】
解:∵ A=x|?2≤x≤2,
B=x|y=lg(x?1)=x|x>1,
∴ A∩B=x|1故选C.
2.
【答案】
A
【考点】
分段函数的应用
函数单调性的性质
【解析】
根据题意,由函数单调性的定义可得a>14?a>0a≥4?a+2?,解可得a的取值范围,即可得答案.
【解答】
解:根据题意,函数f(x)=logax+a,x>1,(4?a)x+2,x≤1?是R上的单调递增函数,
必有a>1,4?a>0,a≥4?a+2,?解得3≤a<4,
即a的取值范围为[3,?4).
故选A.
3.
【答案】
C
【考点】
不等式的基本性质
【解析】
由a、b、c满足a0,b可以为任意实数,即可得出.
【解答】
解:∵ a,b,c满足a∴ a<0,c>0.
A,当a=?2,b=0,c=2时,a2B,当b=0时,ab2C,∵ c>0,aD,∵ a<0,bac,故D错误.
故选C.
4.
【答案】
B
【考点】
函数奇偶性的判断
函数的图象
【解析】
判断函数的奇偶性和零点个数,以及利用极限思想进行求解即可.
【解答】
解:f(?x)=(2?x+2x)ln|?x|
=(2x+2?x)ln|x|=f(x),则f(x)是偶函数,排除D;
由f(x)=0,得ln|x|=0,得|x|=1,
即x=1或x=?1,即f(x)有两个零点,排除C;
当x→+∞,f(x)→+∞,排除A.
故选B.
5.
【答案】
B
【考点】
抛物线的性质
【解析】
根据抛物线上任意点到焦点的距离等于到准线的距离,所以AF等于A到准线x=?1的距离,设A点的横坐标为a,则AF=a+1,再由A到准线x=?3的距离是线段AF长度的2倍,解得a=1,可得选项.
【解答】
解:抛物线y2=4x的准线方程为x=?1,
因为抛物线上任意点到焦点的距离等于到准线的距离,
所以AF等于点A到准线x=?1的距离.
设A点的横坐标为a,则AF=a+1,
因为点A到准线x=?3的距离是线段AF长度的2倍,
所以2a+1=a+3,
解得:a=1,
所以AF=a+1=2.
故选B.
6.
【答案】
D
【考点】
对数函数的单调性与特殊点
幂函数的单调性、奇偶性及其应用
【解析】
先将b,c化成同底的幂,然后利用幂函数、对数函数的单调性能求出a,b,c的大小关系.
【解答】
解:∵ b=1212=123×16=1816,
c=1313=132×16=1916,
且函数y=x16在(0,+∞)上递增,19<18,
∴ 1916<1816<116=1.
∵ a=log23>log22=1,
∴ a,b,c的大小关系为c故选D.
7.
【答案】
B
【考点】
由函数零点求参数取值范围问题
必要条件、充分条件与充要条件的判断
【解析】
此题暂无解析
【解答】
解:易得函数fx=x+log2x?m的定义域是0,+∞.
∵ 函数y=x在0,+∞上为增函数,
函数y=log2x在0,+∞上为增函数,
∴ fx在0,+∞上为增函数.
又∵ fx的图象是连续不断的,
∴ fx在0,+∞上最多有一个零点,
∴ “函数fx在(12,4)上存在零点”?f(12)f4<0,
即(12+log212?m)4+log24?m<0,
∴ (m?6)(m+12)<0,
解得?12即“函数fx在(12,4)上存在零点”?m∈(?12,6).
∵ 1,6?(?12,6),
∴ m∈(?12,6)是m∈(1,6)的必要不充分条件,
即“函数fx在(12,4)上存在零点”是“m∈1,6”的必要不充分条件.
故选B.
8.
【答案】
D
【考点】
函数奇偶性的性质
【解析】
根据奇函数f?x+fx=0求解即可得答案.
【解答】
解:因为函数fx=12x?a+12为奇函数,
所以f?x=12?x?a+12=2x1?a?2x+12,
所以fx+f?x=2x1?a?2x+12+12x?a+12=0,
整理得:?2x2?2a?2x+1?a2x2+a2+12x?a=0,
解得a=1.
故选D.
9.
【答案】
A
【考点】
三角函数的化简求值
三角函数的最值
【解析】
此题暂无解析
【解答】
解:由3sinα+cosα2sinα?3cosα=7,得3tanα+12tanα?3=7,
解得tanα=2,
所以fx=sin2x+2tanα|cosx|?6
=sin2x+4|cosx|?6
=1?|cosx|2+4|cosx|?6
=?(|cosx|?2)2?1.
因为0≤|cosx|≤1,
所以当|cosx|=0时,f(x)min=?5.
故选A.
10.
【答案】
D
【考点】
对数函数的图象与性质
指数函数的图象
函数的图象
幂函数的图像
【解析】
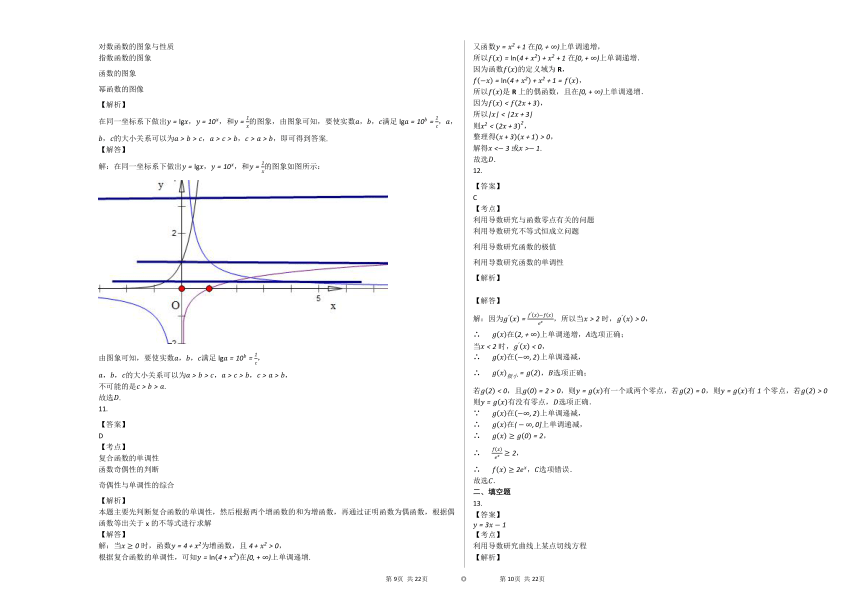
在同一坐标系下做出y=lgx,y=10x,和y=1x的图象,由图象可知,要使实数a,b,c满足lga=10b=1c,a,b,c的大小关系可以为a>b>c,a>c>b,c>a>b,即可得到答案.
【解答】
解:在同一坐标系下做出y=lgx,y=10x,和y=1x的图象如图所示:
由图象可知,要使实数a,b,c满足lga=10b=1c,
a,b,c的大小关系可以为a>b>c,a>c>b,c>a>b,
不可能的是c>b>a.
故选D.
11.
【答案】
D
【考点】
复合函数的单调性
函数奇偶性的判断
奇偶性与单调性的综合
【解析】
本题主要先判断复合函数的单调性,然后根据两个增函数的和为增函数,再通过证明函数为偶函数,根据偶函数等出关于x的不等式进行求解
【解答】
解:当x≥0时,函数y=4+x2为增函数,且4+x2>0,
根据复合函数的单调性,可知y=ln4+x2在[0,+∞)上单调递增.
又函数y=x2+1在[0,+∞)上单调递增,
所以fx=ln4+x2+x2+1在[0,+∞)上单调递增.
因为函数fx的定义域为R,
f?x=ln4+x2+x2+1=fx,
所以fx是R上的偶函数,且在[0,+∞)上单调递增.
因为fx所以|x|<|2x+3|
则x2<2x+32,
整理得x+3x+1>0,
解得x?1.
故选D.
12.
【答案】
C
【考点】
利用导数研究与函数零点有关的问题
利用导数研究不等式恒成立问题
利用导数研究函数的极值
利用导数研究函数的单调性
【解析】
?
【解答】
解:因为g′x=f′x?fxex,所以当x>2时,g′x>0,
∴ gx在2,+∞上单调递增,A选项正确;
当x<2时,g′x<0,
∴ gx在?∞,2上单调递减,
∴ gx极小=g2,B选项正确;
若g2<0,且g0=2>0,则y=gx有一个或两个零点,若g2=0,则y=gx有1个零点,若g2>0则y=gx有没有零点,D选项正确.
∵ gx在?∞,2上单调递减,
∴ gx在(?∞,0]上单调递减,
∴ gx≥g0=2,
∴ fxex≥2,
∴ fx≥2ex,C选项错误.
故选C.
二、填空题
13.
【答案】
y=3x?1
【考点】
利用导数研究曲线上某点切线方程
【解析】
?
【解答】
解:∵ 曲线f(x)=2+lnxx,
∴ f′(x)=?1?lnxx2,
当x=1时,f(1)=2,k=f′(1)=?1,
∴ 切线方程为:y?2=?1(x?1),
即x+y?3=0.
故答案为:x+y?3=0.
14.
【答案】
?34
【考点】
函数的周期性
函数奇偶性的性质
函数的求值
【解析】
由奇函数的性质可得,f(?92)=?f(92),由周期性可得f(92)=f(92?4)=f(12),进而得解.
【解答】
解:由题意可得,
f(?92)=?f(92)=?f(92?4)=?f(12)
=?12×(1+12)=?12×32=?34.
故答案为:?34.
15.
【答案】
4
【考点】
基本不等式在最值问题中的应用
基本不等式
【解析】
利用指数运算求得x+3y=1,然后将代数式1x+13y与x+3y相乘,展开后利用基本不等式可求得1x+13y的最小值.
【解答】
解:∵ 2x?8y=2x+3y=2,
∴ x+3y=1.
∵ x>0,y>0,
∴ 原式=1x+13y(x+3y)
=2+3yx+x3y
≥2+23yx?x3y=4,
当且仅当3yx=x3y,即x=12,y=16时,等号成立.
故答案为:4.
16.
【答案】
29π
【考点】
球内接多面体
球的表面积和体积
【解析】
由三棱锥的侧面积及所给的棱长可得AB的值,再由题意将该三棱锥放在长方体中,由长方体的对角线的长度等于其外接球的直径(2R)可得4R2的值,进而求出外接球的表面积.
【解答】
解:三棱锥B?ACD的侧面积:
S=S△ABD+S△ABC+SBCD
=12(AB?BD+AB?BC+BC?CD)
=12(4AB+2AB+2×4)=13,
解得:AB=3.
将此三棱锥放在长方体中可得,三棱锥的外接球与长方体的外接球为同一个,且长方体的外接球的直径2R等于长方体的对角线的长度,
所以(2R)2=AB2+BC2+BD2=32+22+42=29,
即4R2=29,
所以外接球的表面积S表=4πR2=29π.
故答案为:29π.
三、解答题
17.
【答案】
解:(1)由an+1=2Sn+1①,
可得an=2Sn?1+1(n≥2)②,
①?②得,an+1?an=2an,
即an+1=3an(n≥2).
又a1=1,
所以a2=2S1+1=2a1+1=3,
满足an+1=3an,
故数列{an}是首项为1,公比为3的等比数列,
所以an=3n?1.
因为点P(bn,bn+1)在直线x?y+2=0上,
所以bn+1?bn=2,
则数列{bn}是首项为1,公差为2的等差数列,
则bn=1+(n?1)?2=2n?1.
(2)由(1)得an=3n?1,bn=2n?1,
则cn=bnan=2n?13n?1,
所以Tn=130+331+532+?+2n?13n?1①,
则13Tn=131+332+533+?+2n?33n?1+2n?13n②,
①?②得,23Tn=1+23+232+?+23n?1?2n?13n
=1+2×13[1?(13)n?1]1?13?2n?13n
=2?13n?1?2n?13n,
所以Tn=3?12?3n?2?2n?12?3n?1=3?n+13n?1.
【考点】
数列的求和
等比数列的通项公式
等差数列的通项公式
【解析】
(1)求数列{an},{bn}的通项公式,先要根据已知条件判断数列是否为等差(比)数列,由a1=1,an+1=2Sn+1,得到数列{an}为等比数列,而由数列{bn}满足a1=b1,点P(bn,?bn+1)在直线x?y+2=0上,得数列{bn}是一个等差数列.求出对应的基本量,代入即可求出数列{an},{bn}的通项公式.
(2)由(1)中结论,可得cn=bnan,即数列{cn}的通项公式可以分解为一个等差数列和一个等比数列相乘的形式,则可以用错位相消法,求数列{cn}的前n项和Tn.
【解答】
解:(1)由an+1=2Sn+1①,
可得an=2Sn?1+1(n≥2)②,
①?②得,an+1?an=2an,
即an+1=3an(n≥2).
又a1=1,
所以a2=2S1+1=2a1+1=3,
满足an+1=3an,
故数列{an}是首项为1,公比为3的等比数列,
所以an=3n?1.
因为点P(bn,bn+1)在直线x?y+2=0上,
所以bn+1?bn=2,
则数列{bn}是首项为1,公差为2的等差数列,
则bn=1+(n?1)?2=2n?1.
(2)由(1)得an=3n?1,bn=2n?1,
则cn=bnan=2n?13n?1,
所以Tn=130+331+532+?+2n?13n?1①,
则13Tn=131+332+533+?+2n?33n?1+2n?13n②,
①?②得,23Tn=1+23+232+?+23n?1?2n?13n
=1+2×13[1?(13)n?1]1?13?2n?13n
=2?13n?1?2n?13n,
所以Tn=3?12?3n?2?2n?12?3n?1=3?n+13n?1.
18.
【答案】
解:(1)依题fx=3sin2x+cos2x=2sin2x+π6,
令π2+2kπ<2x+π6<3π2+2kπ(k∈Z),
解得π6+kπ又x∈0,π,
故函数fx的单调递减区间为:?π6,2π3.
(2)由fC=1?2sin2C+π6=1?sin2C+π6=12,
又C∈0,π,故C=π3.
依题S△ABC=12?ab?sinC=34a?b=235a2?b=85a.
在△ABC中,由余弦定理得:?c2=85a2+a2?85a2=4925a2?c=75a,
故bc=87.
【考点】
两角和与差的正弦公式
三角函数的化简求值
余弦定理
正弦定理
正弦函数的单调性
【解析】
?
?
【解答】
解:(1)依题fx=3sin2x+cos2x=2sin2x+π6,
令π2+2kπ<2x+π6<3π2+2kπ(k∈Z),
解得π6+kπ又x∈0,π,
故函数fx的单调递减区间为:?π6,2π3.
(2)由fC=1?2sin2C+π6=1?sin2C+π6=12,
又C∈0,π,故C=π3.
依题S△ABC=12?ab?sinC=34a?b=235a2?b=85a.
在△ABC中,由余弦定理得:?c2=85a2+a2?85a2=4925a2?c=75a,
故bc=87.
19.
【答案】
(1)证明:AB是底面圆的直径,AC与圆切于点A,所以AC⊥AB,
又因为PO⊥底面ABC,
所以PO⊥AC.
因为PO∩AB=O,
所以AC⊥面PAB,
所以AC⊥PB.
又因为在三角形PAB中,PA=PB=22AB,
所以PA⊥PB.
因为PA∩AC=A,
所以PB⊥面PAC.
因为PB?面PBC,
所以平面PBC⊥平面PAC?.?
(2)解:因为OB⊥PO,OD⊥PO,
所以∠BOD为二面角B?PO?D的平面角,
所以∠BOD=2π3,
如图建立空间直角坐标系,易知OB=1,
则A0,?1,0,B0,1,0,?D(32,?12,0),C233,?1,0,P(0,0,1),?E33,?12,12,
由(1)可知BP→=(0,?1,1)为平面PAC法向量.
设平面ODE的法向量为n→=x,y,z,
OE→=33,?12,12,OE→?n→=0?33x?12y+12z=0,
OD→=32,?12,0,OD→?n→=0?32x?12y=0,
解得:n→=3,3,1,
cosθ=|n→?BP→||n→||BP→|=22×13=2613?,
即平面PAC与平面DOE所成锐二面角的余弦值为2613?.
【考点】
二面角的平面角及求法
用空间向量求平面间的夹角
平面与平面垂直的判定
【解析】
此题暂无解析
【解答】
(1)证明:AB是底面圆的直径,AC与圆切于点A,所以AC⊥AB,
又因为PO⊥底面ABC,
所以PO⊥AC.
因为PO∩AB=O,
所以AC⊥面PAB,
所以AC⊥PB.
又因为在三角形PAB中,PA=PB=22AB,
所以PA⊥PB.
因为PA∩AC=A,
所以PB⊥面PAC.
因为PB?面PBC,
所以平面PBC⊥平面PAC?.?
(2)解:因为OB⊥PO,OD⊥PO,
所以∠BOD为二面角B?PO?D的平面角,
所以∠BOD=2π3,
如图建立空间直角坐标系,易知OB=1,
则A0,?1,0,B0,1,0,?D(32,?12,0),C233,?1,0,P(0,0,1),?E33,?12,12,
由(1)可知BP→=(0,?1,1)为平面PAC法向量.
设平面ODE的法向量为n→=x,y,z,
OE→=33,?12,12,OE→?n→=0?33x?12y+12z=0,
OD→=32,?12,0,OD→?n→=0?32x?12y=0,
解得:n→=3,3,1,
cosθ=|n→?BP→||n→||BP→|=22×13=2613?,
即平面PAC与平面DOE所成锐二面角的余弦值为2613?.
20.
【答案】
解:(1)由题意得,2a=42,得a=22,
e=ca=22,可得c=2,
所以b2=a2?c2=4,
所以椭圆C的标准方程为x28+y24=1.
(2)设Mx1,y1,Nx2,y2,将y=kx+m代入椭圆方程,
消去y得,1+2k2x2+4kmx+2m2?8=0,
所以由Δ>0,得m2<8k2+4①,
由根与系数关系得x1+x2=?4km1+2k2,则y1+y2=2m1+2k2,
所以线段 MN的中点P的坐标为?2km1+2k2,m1+2k2.
又线段 MN的垂直平分线l′的方程为y=?1kx?1,
由点P在直线l′,得m1+2k2=?1k?2km1+2k2?1,
所以m=?1+2k2k②,由①②得,k2>12,
即k>22或k所以实数k的取值范围是(?∞,?22)∪(22,+∞).
【考点】
圆锥曲线中的范围与最值问题
圆锥曲线的综合问题
椭圆的离心率
直线与椭圆结合的最值问题
椭圆的标准方程
【解析】
【解答】
解:(1)由题意得,2a=42,得a=22,
e=ca=22,可得c=2,
所以b2=a2?c2=4,
所以椭圆C的标准方程为x28+y24=1.
(2)设Mx1,y1,Nx2,y2,将y=kx+m代入椭圆方程,
消去y得,1+2k2x2+4kmx+2m2?8=0,
所以由Δ>0,得m2<8k2+4①,
由根与系数关系得x1+x2=?4km1+2k2,则y1+y2=2m1+2k2,
所以线段?MN的中点P的坐标为?2km1+2k2,m1+2k2.
又线段?MN的垂直平分线l′的方程为y=?1kx?1,
由点P在直线l′,得m1+2k2=?1k?2km1+2k2?1,
所以m=?1+2k2k②,由①②得,k2>12,
即k>22或k所以实数k的取值范围是(?∞,?22)∪(22,+∞).
21.
【答案】
解:(1)由fx=exax+1得f′x=exax+a+1,
①当a=0时,?f′x>0,fx在?∞,+∞上单调递增;
②当a>0时,由f′x>0?x>?a+1a
故fx在?a+1a,+∞上单调递增,在(?∞,?a+1a)上单调递减;
③当a<0时,由f′x>0?x故fx在?∞,?a+1a上单调递增,在?a+1a,+∞上单调递减.
(2)当a=1时,?fx=exx+1,
由exx+1=x+3?ex=x+3x+1x≠?1,
由图像观察可知它们有两个交点,记gx=ex?x+3x+1x≠?1,
注意至g′x=ex+2x+12>0
故gx在?∞,?1为增,在?1,+∞也为增,
而g?4=e?4?13<0,?g?3=e?3>0,
故?4又g0=1?3<0,g1=e?2>0,又得0整数m的所有可能的值为?4,0.
【考点】
利用导数研究函数的单调性
由函数零点求参数取值范围问题
【解析】
?
?
【解答】
解:(1)由fx=exax+1得f′x=exax+a+1,
①当a=0时,?f′x>0,fx在?∞,+∞上单调递增;
②当a>0时,由f′x>0?x>?a+1a
故fx在?a+1a,+∞上单调递增,在(?∞,?a+1a)上单调递减;
③当a<0时,由f′x>0?x故fx在?∞,?a+1a上单调递增,在?a+1a,+∞上单调递减.
(2)当a=1时,?fx=exx+1,
由exx+1=x+3?ex=x+3x+1x≠?1,
由图像观察可知它们有两个交点,记gx=ex?x+3x+1x≠?1,
注意至g′x=ex+2x+12>0
故gx在?∞,?1为增,在?1,+∞也为增,
而g?4=e?4?13<0,?g?3=e?3>0,
故?4又g0=1?3<0,g1=e?2>0,又得0整数m的所有可能的值为?4,0.
22.
【答案】
解:(1)?将C1的参数方程化为普通方程为(x?1)2+y2=3,
即x2+y2?2x?2=0,
∴ C1的极坐标方程为ρ2?2ρcosθ?2=0.
将C2的极坐标方程ρ=1化为直角坐标方程为x2+y2=1.
(2)将θ=π3(ρ≥0),代入C1:ρ2?2ρcosθ?2=0,
整理得ρ2?ρ?2=0,
解得:ρ1=2,即|OA|=2.
∵ 曲线C2是圆心在原点,半径为1的圆,
∴ 射线θ=π3(ρ≥0)与C2相交,则ρ2=1,即|OB|=1,
故|BA|=|ρ1?ρ2|=2?1=1.
【考点】
直线的极坐标方程
圆的参数方程
圆的极坐标方程
【解析】
(Ⅰ)?将C1的参数方程化为普通方程为(x?1)2+y2=3,即x2+y2?2x?2=0,利用互化公式可得:C1的极坐标方程.同理利用互化公式将C2的极坐标方程ρ=1化为直角坐标方程.
(Ⅱ)将θ=π3(ρ≥0),代入C1:ρ2?2ρcosθ?2=0.整理得ρ2?ρ?2=0,解得:ρ1,可得|OA|=ρ1.把射线θ=π3(ρ≥0)代入C2的方程,解得ρ2=1,即|OB|=ρ2.可得|BA|=|ρ1?ρ2|.
【解答】
解:(1)?将C1的参数方程化为普通方程为(x?1)2+y2=3,
即x2+y2?2x?2=0,
∴ C1的极坐标方程为ρ2?2ρcosθ?2=0.
将C2的极坐标方程ρ=1化为直角坐标方程为x2+y2=1.
(2)将θ=π3(ρ≥0),代入C1:ρ2?2ρcosθ?2=0,
整理得ρ2?ρ?2=0,
解得:ρ1=2,即|OA|=2.
∵ 曲线C2是圆心在原点,半径为1的圆,
∴ 射线θ=π3(ρ≥0)与C2相交,则ρ2=1,即|OB|=1,
故|BA|=|ρ1?ρ2|=2?1=1.
一、选择题
?
1. 已知集合A={x|?2≤x≤2},B={x|y=lg(x?1)},则A∩B=(? ? ? ? )
A.x|x≥?2 B.x|1
2. 已知函数f(x)=logax+a,x>1,(4?a)x+2,x≤1?是R上的单调递增函数,则a的取值范围是(? ? ? ? )
A.[3,?4) B.[2,?4) C.(1,?4) D.(1,?3]
?
3. 已知实数a,b,c满足a
A.a2
4. 已知函数f(x)=(2x+2?x)ln|x|的图象大致为(? ? ? ? )
A. B.
C. D.
?
5. 抛物线C:y2=4x的焦点为F,点A在抛物线上,且点A到直线x=?3的距离是线段AF长度的2倍,则线段AF的长度为(? ? ? ? )
A.1 B.2 C.3 D.4
?
6. 已知a=log23, b=1212 ,c=1313,则a,b,c的大小关系是(????????)
A.a
7. 设函数fx=x+log2x?m,则“函数fx在(12,4)上存在零点”是“m∈1,6”的(? ? ? ? )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
?
8. 已知函数fx=12x?a+12为奇函数,则a=(? ? ? ? ? ?)
A.?2 B.?1 C.0 D.1
?
9. 已知3sinα+cosα2sinα?3cosα=7,则函数fx=sin2x+2tanα|cosx|?6的最小值为(? ? ? ? )
A.?5 B.?3 C.?2 D.?1
?
10. 已知实数a,b,c满足lga=10b=1c,则下列关系式中不可能成立的是(? ? ? ? )
A.a>b>c? B.a>c>b? C.c>a>b? D.c>b>a
?
11. 设函数fx=ln4+x2+x2+1,则使得fx
A.?3,+∞ B.?∞,?3
C.?3,?1 D.?∞,?3∪?1,+∞
?
12. 已知函数y=fx在R上可导且f0=2,其导函数f′x满足,f′x?fxx?2>0,对于函数gx=fxex,下列结论错误的是(????????)
A.函数gx在2,+∞上为单调递增函数
B.x=2是函数gx的极小值点
C.x≤0时,不等式fx≤2e恒成立
D.函数gx至多有两个零点
二、填空题
?
13. 曲线y=2+lnxx在点x=1处的切线方程是________.
?
14. 设f(x)是周期为4的奇函数,当0≤x≤1时,f(x)=x?(1+x),则f(?92)=________.
?
15. 已知x>0,y>0,2x?8y=2,则1x+13y的最小值是________ .
?
16. 在三棱锥B?ACD中,BA,BC,BD两两垂直,BC=2,BD=4,三棱锥的侧面积为13,则该三棱锥外接球的表面积为________.
三、解答题
?
17. 设数列{an}的前n项和为Sn,且a1=1,an+1=2Sn+1,数列{bn}满足a1=b1,点P(bn,bn+1)在直线x?y+2=0上,n∈N*.
(1)求数列{an},{bn}的通项公式;
(2)设cn=bnan,求数列{cn}的前n项和Tn.
?
18. 已知函数fx=23sinxcosx+2cos2x?1,x∈0,π,△ABC中,角A,B,C所对的边分别为a,b,c, △ABC的面积为235a2.
(1)求函数fx的单调递减区间;
(2)若fC=1,求bc的值.
?
19. 如图,在以P为顶点的圆锥中,母线长为2,底面圆的直径AB长为2,O为圆心.C是圆O所在平面上一点,且AC与圆O相切,连接BC交圆于点D.连接PD,PC,E是PC的中点,连接OE,ED.
(1)求证:平面PBC⊥平面PAC;
(2)若二面角B?PO?D的大小为2π3,求平面PAC与平面DOE所成锐二面角的余弦值.
?
20. 已知椭圆C:x2a2+y2b2=1a>b>0的离心率为22,长轴长为42.
(1)求椭圆C的标准方程;
(2)若直线l:y=kx+mk≠0与椭圆C交于不同的两点M,N,且线段MN的垂直平分线过定点1,0,求实数k的取值范围.
?
21. 已知函数fx=exax+1.
(1)讨论函数fx的单调性;
(2)当a=1时,若P为直线y=x+3与函数fx图像的一个公共点,其横坐标为t,且t∈m,m+1,求整数m的所有可能的值.
?
22. 在平面直角坐标系xOy中,曲线C1的参数方程是x=1+3cosα,y=3sinα?(α为参数),以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρ=1.
(1)分别写出C1的极坐标方程和C2的直角坐标方程;
(2)若射线l的极坐标方程θ=π3(ρ≥0),且l分别交曲线C1,C2于A,B两点,求|AB|.
参考答案与试题解析
2020-2021学年江西赣州高三上数学月考试卷
一、选择题
1.
【答案】
C
【考点】
对数函数的定义域
交集及其运算
【解析】
化简集合B,根据交集的定义即可得解.
【解答】
解:∵ A=x|?2≤x≤2,
B=x|y=lg(x?1)=x|x>1,
∴ A∩B=x|1
2.
【答案】
A
【考点】
分段函数的应用
函数单调性的性质
【解析】
根据题意,由函数单调性的定义可得a>14?a>0a≥4?a+2?,解可得a的取值范围,即可得答案.
【解答】
解:根据题意,函数f(x)=logax+a,x>1,(4?a)x+2,x≤1?是R上的单调递增函数,
必有a>1,4?a>0,a≥4?a+2,?解得3≤a<4,
即a的取值范围为[3,?4).
故选A.
3.
【答案】
C
【考点】
不等式的基本性质
【解析】
由a、b、c满足a
【解答】
解:∵ a,b,c满足a
A,当a=?2,b=0,c=2时,a2
故选C.
4.
【答案】
B
【考点】
函数奇偶性的判断
函数的图象
【解析】
判断函数的奇偶性和零点个数,以及利用极限思想进行求解即可.
【解答】
解:f(?x)=(2?x+2x)ln|?x|
=(2x+2?x)ln|x|=f(x),则f(x)是偶函数,排除D;
由f(x)=0,得ln|x|=0,得|x|=1,
即x=1或x=?1,即f(x)有两个零点,排除C;
当x→+∞,f(x)→+∞,排除A.
故选B.
5.
【答案】
B
【考点】
抛物线的性质
【解析】
根据抛物线上任意点到焦点的距离等于到准线的距离,所以AF等于A到准线x=?1的距离,设A点的横坐标为a,则AF=a+1,再由A到准线x=?3的距离是线段AF长度的2倍,解得a=1,可得选项.
【解答】
解:抛物线y2=4x的准线方程为x=?1,
因为抛物线上任意点到焦点的距离等于到准线的距离,
所以AF等于点A到准线x=?1的距离.
设A点的横坐标为a,则AF=a+1,
因为点A到准线x=?3的距离是线段AF长度的2倍,
所以2a+1=a+3,
解得:a=1,
所以AF=a+1=2.
故选B.
6.
【答案】
D
【考点】
对数函数的单调性与特殊点
幂函数的单调性、奇偶性及其应用
【解析】
先将b,c化成同底的幂,然后利用幂函数、对数函数的单调性能求出a,b,c的大小关系.
【解答】
解:∵ b=1212=123×16=1816,
c=1313=132×16=1916,
且函数y=x16在(0,+∞)上递增,19<18,
∴ 1916<1816<116=1.
∵ a=log23>log22=1,
∴ a,b,c的大小关系为c
7.
【答案】
B
【考点】
由函数零点求参数取值范围问题
必要条件、充分条件与充要条件的判断
【解析】
此题暂无解析
【解答】
解:易得函数fx=x+log2x?m的定义域是0,+∞.
∵ 函数y=x在0,+∞上为增函数,
函数y=log2x在0,+∞上为增函数,
∴ fx在0,+∞上为增函数.
又∵ fx的图象是连续不断的,
∴ fx在0,+∞上最多有一个零点,
∴ “函数fx在(12,4)上存在零点”?f(12)f4<0,
即(12+log212?m)4+log24?m<0,
∴ (m?6)(m+12)<0,
解得?12
∵ 1,6?(?12,6),
∴ m∈(?12,6)是m∈(1,6)的必要不充分条件,
即“函数fx在(12,4)上存在零点”是“m∈1,6”的必要不充分条件.
故选B.
8.
【答案】
D
【考点】
函数奇偶性的性质
【解析】
根据奇函数f?x+fx=0求解即可得答案.
【解答】
解:因为函数fx=12x?a+12为奇函数,
所以f?x=12?x?a+12=2x1?a?2x+12,
所以fx+f?x=2x1?a?2x+12+12x?a+12=0,
整理得:?2x2?2a?2x+1?a2x2+a2+12x?a=0,
解得a=1.
故选D.
9.
【答案】
A
【考点】
三角函数的化简求值
三角函数的最值
【解析】
此题暂无解析
【解答】
解:由3sinα+cosα2sinα?3cosα=7,得3tanα+12tanα?3=7,
解得tanα=2,
所以fx=sin2x+2tanα|cosx|?6
=sin2x+4|cosx|?6
=1?|cosx|2+4|cosx|?6
=?(|cosx|?2)2?1.
因为0≤|cosx|≤1,
所以当|cosx|=0时,f(x)min=?5.
故选A.
10.
【答案】
D
【考点】
对数函数的图象与性质
指数函数的图象
函数的图象
幂函数的图像
【解析】
在同一坐标系下做出y=lgx,y=10x,和y=1x的图象,由图象可知,要使实数a,b,c满足lga=10b=1c,a,b,c的大小关系可以为a>b>c,a>c>b,c>a>b,即可得到答案.
【解答】
解:在同一坐标系下做出y=lgx,y=10x,和y=1x的图象如图所示:
由图象可知,要使实数a,b,c满足lga=10b=1c,
a,b,c的大小关系可以为a>b>c,a>c>b,c>a>b,
不可能的是c>b>a.
故选D.
11.
【答案】
D
【考点】
复合函数的单调性
函数奇偶性的判断
奇偶性与单调性的综合
【解析】
本题主要先判断复合函数的单调性,然后根据两个增函数的和为增函数,再通过证明函数为偶函数,根据偶函数等出关于x的不等式进行求解
【解答】
解:当x≥0时,函数y=4+x2为增函数,且4+x2>0,
根据复合函数的单调性,可知y=ln4+x2在[0,+∞)上单调递增.
又函数y=x2+1在[0,+∞)上单调递增,
所以fx=ln4+x2+x2+1在[0,+∞)上单调递增.
因为函数fx的定义域为R,
f?x=ln4+x2+x2+1=fx,
所以fx是R上的偶函数,且在[0,+∞)上单调递增.
因为fx
则x2<2x+32,
整理得x+3x+1>0,
解得x?1.
故选D.
12.
【答案】
C
【考点】
利用导数研究与函数零点有关的问题
利用导数研究不等式恒成立问题
利用导数研究函数的极值
利用导数研究函数的单调性
【解析】
?
【解答】
解:因为g′x=f′x?fxex,所以当x>2时,g′x>0,
∴ gx在2,+∞上单调递增,A选项正确;
当x<2时,g′x<0,
∴ gx在?∞,2上单调递减,
∴ gx极小=g2,B选项正确;
若g2<0,且g0=2>0,则y=gx有一个或两个零点,若g2=0,则y=gx有1个零点,若g2>0则y=gx有没有零点,D选项正确.
∵ gx在?∞,2上单调递减,
∴ gx在(?∞,0]上单调递减,
∴ gx≥g0=2,
∴ fxex≥2,
∴ fx≥2ex,C选项错误.
故选C.
二、填空题
13.
【答案】
y=3x?1
【考点】
利用导数研究曲线上某点切线方程
【解析】
?
【解答】
解:∵ 曲线f(x)=2+lnxx,
∴ f′(x)=?1?lnxx2,
当x=1时,f(1)=2,k=f′(1)=?1,
∴ 切线方程为:y?2=?1(x?1),
即x+y?3=0.
故答案为:x+y?3=0.
14.
【答案】
?34
【考点】
函数的周期性
函数奇偶性的性质
函数的求值
【解析】
由奇函数的性质可得,f(?92)=?f(92),由周期性可得f(92)=f(92?4)=f(12),进而得解.
【解答】
解:由题意可得,
f(?92)=?f(92)=?f(92?4)=?f(12)
=?12×(1+12)=?12×32=?34.
故答案为:?34.
15.
【答案】
4
【考点】
基本不等式在最值问题中的应用
基本不等式
【解析】
利用指数运算求得x+3y=1,然后将代数式1x+13y与x+3y相乘,展开后利用基本不等式可求得1x+13y的最小值.
【解答】
解:∵ 2x?8y=2x+3y=2,
∴ x+3y=1.
∵ x>0,y>0,
∴ 原式=1x+13y(x+3y)
=2+3yx+x3y
≥2+23yx?x3y=4,
当且仅当3yx=x3y,即x=12,y=16时,等号成立.
故答案为:4.
16.
【答案】
29π
【考点】
球内接多面体
球的表面积和体积
【解析】
由三棱锥的侧面积及所给的棱长可得AB的值,再由题意将该三棱锥放在长方体中,由长方体的对角线的长度等于其外接球的直径(2R)可得4R2的值,进而求出外接球的表面积.
【解答】
解:三棱锥B?ACD的侧面积:
S=S△ABD+S△ABC+SBCD
=12(AB?BD+AB?BC+BC?CD)
=12(4AB+2AB+2×4)=13,
解得:AB=3.
将此三棱锥放在长方体中可得,三棱锥的外接球与长方体的外接球为同一个,且长方体的外接球的直径2R等于长方体的对角线的长度,
所以(2R)2=AB2+BC2+BD2=32+22+42=29,
即4R2=29,
所以外接球的表面积S表=4πR2=29π.
故答案为:29π.
三、解答题
17.
【答案】
解:(1)由an+1=2Sn+1①,
可得an=2Sn?1+1(n≥2)②,
①?②得,an+1?an=2an,
即an+1=3an(n≥2).
又a1=1,
所以a2=2S1+1=2a1+1=3,
满足an+1=3an,
故数列{an}是首项为1,公比为3的等比数列,
所以an=3n?1.
因为点P(bn,bn+1)在直线x?y+2=0上,
所以bn+1?bn=2,
则数列{bn}是首项为1,公差为2的等差数列,
则bn=1+(n?1)?2=2n?1.
(2)由(1)得an=3n?1,bn=2n?1,
则cn=bnan=2n?13n?1,
所以Tn=130+331+532+?+2n?13n?1①,
则13Tn=131+332+533+?+2n?33n?1+2n?13n②,
①?②得,23Tn=1+23+232+?+23n?1?2n?13n
=1+2×13[1?(13)n?1]1?13?2n?13n
=2?13n?1?2n?13n,
所以Tn=3?12?3n?2?2n?12?3n?1=3?n+13n?1.
【考点】
数列的求和
等比数列的通项公式
等差数列的通项公式
【解析】
(1)求数列{an},{bn}的通项公式,先要根据已知条件判断数列是否为等差(比)数列,由a1=1,an+1=2Sn+1,得到数列{an}为等比数列,而由数列{bn}满足a1=b1,点P(bn,?bn+1)在直线x?y+2=0上,得数列{bn}是一个等差数列.求出对应的基本量,代入即可求出数列{an},{bn}的通项公式.
(2)由(1)中结论,可得cn=bnan,即数列{cn}的通项公式可以分解为一个等差数列和一个等比数列相乘的形式,则可以用错位相消法,求数列{cn}的前n项和Tn.
【解答】
解:(1)由an+1=2Sn+1①,
可得an=2Sn?1+1(n≥2)②,
①?②得,an+1?an=2an,
即an+1=3an(n≥2).
又a1=1,
所以a2=2S1+1=2a1+1=3,
满足an+1=3an,
故数列{an}是首项为1,公比为3的等比数列,
所以an=3n?1.
因为点P(bn,bn+1)在直线x?y+2=0上,
所以bn+1?bn=2,
则数列{bn}是首项为1,公差为2的等差数列,
则bn=1+(n?1)?2=2n?1.
(2)由(1)得an=3n?1,bn=2n?1,
则cn=bnan=2n?13n?1,
所以Tn=130+331+532+?+2n?13n?1①,
则13Tn=131+332+533+?+2n?33n?1+2n?13n②,
①?②得,23Tn=1+23+232+?+23n?1?2n?13n
=1+2×13[1?(13)n?1]1?13?2n?13n
=2?13n?1?2n?13n,
所以Tn=3?12?3n?2?2n?12?3n?1=3?n+13n?1.
18.
【答案】
解:(1)依题fx=3sin2x+cos2x=2sin2x+π6,
令π2+2kπ<2x+π6<3π2+2kπ(k∈Z),
解得π6+kπ
故函数fx的单调递减区间为:?π6,2π3.
(2)由fC=1?2sin2C+π6=1?sin2C+π6=12,
又C∈0,π,故C=π3.
依题S△ABC=12?ab?sinC=34a?b=235a2?b=85a.
在△ABC中,由余弦定理得:?c2=85a2+a2?85a2=4925a2?c=75a,
故bc=87.
【考点】
两角和与差的正弦公式
三角函数的化简求值
余弦定理
正弦定理
正弦函数的单调性
【解析】
?
?
【解答】
解:(1)依题fx=3sin2x+cos2x=2sin2x+π6,
令π2+2kπ<2x+π6<3π2+2kπ(k∈Z),
解得π6+kπ
故函数fx的单调递减区间为:?π6,2π3.
(2)由fC=1?2sin2C+π6=1?sin2C+π6=12,
又C∈0,π,故C=π3.
依题S△ABC=12?ab?sinC=34a?b=235a2?b=85a.
在△ABC中,由余弦定理得:?c2=85a2+a2?85a2=4925a2?c=75a,
故bc=87.
19.
【答案】
(1)证明:AB是底面圆的直径,AC与圆切于点A,所以AC⊥AB,
又因为PO⊥底面ABC,
所以PO⊥AC.
因为PO∩AB=O,
所以AC⊥面PAB,
所以AC⊥PB.
又因为在三角形PAB中,PA=PB=22AB,
所以PA⊥PB.
因为PA∩AC=A,
所以PB⊥面PAC.
因为PB?面PBC,
所以平面PBC⊥平面PAC?.?
(2)解:因为OB⊥PO,OD⊥PO,
所以∠BOD为二面角B?PO?D的平面角,
所以∠BOD=2π3,
如图建立空间直角坐标系,易知OB=1,
则A0,?1,0,B0,1,0,?D(32,?12,0),C233,?1,0,P(0,0,1),?E33,?12,12,
由(1)可知BP→=(0,?1,1)为平面PAC法向量.
设平面ODE的法向量为n→=x,y,z,
OE→=33,?12,12,OE→?n→=0?33x?12y+12z=0,
OD→=32,?12,0,OD→?n→=0?32x?12y=0,
解得:n→=3,3,1,
cosθ=|n→?BP→||n→||BP→|=22×13=2613?,
即平面PAC与平面DOE所成锐二面角的余弦值为2613?.
【考点】
二面角的平面角及求法
用空间向量求平面间的夹角
平面与平面垂直的判定
【解析】
此题暂无解析
【解答】
(1)证明:AB是底面圆的直径,AC与圆切于点A,所以AC⊥AB,
又因为PO⊥底面ABC,
所以PO⊥AC.
因为PO∩AB=O,
所以AC⊥面PAB,
所以AC⊥PB.
又因为在三角形PAB中,PA=PB=22AB,
所以PA⊥PB.
因为PA∩AC=A,
所以PB⊥面PAC.
因为PB?面PBC,
所以平面PBC⊥平面PAC?.?
(2)解:因为OB⊥PO,OD⊥PO,
所以∠BOD为二面角B?PO?D的平面角,
所以∠BOD=2π3,
如图建立空间直角坐标系,易知OB=1,
则A0,?1,0,B0,1,0,?D(32,?12,0),C233,?1,0,P(0,0,1),?E33,?12,12,
由(1)可知BP→=(0,?1,1)为平面PAC法向量.
设平面ODE的法向量为n→=x,y,z,
OE→=33,?12,12,OE→?n→=0?33x?12y+12z=0,
OD→=32,?12,0,OD→?n→=0?32x?12y=0,
解得:n→=3,3,1,
cosθ=|n→?BP→||n→||BP→|=22×13=2613?,
即平面PAC与平面DOE所成锐二面角的余弦值为2613?.
20.
【答案】
解:(1)由题意得,2a=42,得a=22,
e=ca=22,可得c=2,
所以b2=a2?c2=4,
所以椭圆C的标准方程为x28+y24=1.
(2)设Mx1,y1,Nx2,y2,将y=kx+m代入椭圆方程,
消去y得,1+2k2x2+4kmx+2m2?8=0,
所以由Δ>0,得m2<8k2+4①,
由根与系数关系得x1+x2=?4km1+2k2,则y1+y2=2m1+2k2,
所以线段 MN的中点P的坐标为?2km1+2k2,m1+2k2.
又线段 MN的垂直平分线l′的方程为y=?1kx?1,
由点P在直线l′,得m1+2k2=?1k?2km1+2k2?1,
所以m=?1+2k2k②,由①②得,k2>12,
即k>22或k所以实数k的取值范围是(?∞,?22)∪(22,+∞).
【考点】
圆锥曲线中的范围与最值问题
圆锥曲线的综合问题
椭圆的离心率
直线与椭圆结合的最值问题
椭圆的标准方程
【解析】
【解答】
解:(1)由题意得,2a=42,得a=22,
e=ca=22,可得c=2,
所以b2=a2?c2=4,
所以椭圆C的标准方程为x28+y24=1.
(2)设Mx1,y1,Nx2,y2,将y=kx+m代入椭圆方程,
消去y得,1+2k2x2+4kmx+2m2?8=0,
所以由Δ>0,得m2<8k2+4①,
由根与系数关系得x1+x2=?4km1+2k2,则y1+y2=2m1+2k2,
所以线段?MN的中点P的坐标为?2km1+2k2,m1+2k2.
又线段?MN的垂直平分线l′的方程为y=?1kx?1,
由点P在直线l′,得m1+2k2=?1k?2km1+2k2?1,
所以m=?1+2k2k②,由①②得,k2>12,
即k>22或k所以实数k的取值范围是(?∞,?22)∪(22,+∞).
21.
【答案】
解:(1)由fx=exax+1得f′x=exax+a+1,
①当a=0时,?f′x>0,fx在?∞,+∞上单调递增;
②当a>0时,由f′x>0?x>?a+1a
故fx在?a+1a,+∞上单调递增,在(?∞,?a+1a)上单调递减;
③当a<0时,由f′x>0?x故fx在?∞,?a+1a上单调递增,在?a+1a,+∞上单调递减.
(2)当a=1时,?fx=exx+1,
由exx+1=x+3?ex=x+3x+1x≠?1,
由图像观察可知它们有两个交点,记gx=ex?x+3x+1x≠?1,
注意至g′x=ex+2x+12>0
故gx在?∞,?1为增,在?1,+∞也为增,
而g?4=e?4?13<0,?g?3=e?3>0,
故?4
【考点】
利用导数研究函数的单调性
由函数零点求参数取值范围问题
【解析】
?
?
【解答】
解:(1)由fx=exax+1得f′x=exax+a+1,
①当a=0时,?f′x>0,fx在?∞,+∞上单调递增;
②当a>0时,由f′x>0?x>?a+1a
故fx在?a+1a,+∞上单调递增,在(?∞,?a+1a)上单调递减;
③当a<0时,由f′x>0?x故fx在?∞,?a+1a上单调递增,在?a+1a,+∞上单调递减.
(2)当a=1时,?fx=exx+1,
由exx+1=x+3?ex=x+3x+1x≠?1,
由图像观察可知它们有两个交点,记gx=ex?x+3x+1x≠?1,
注意至g′x=ex+2x+12>0
故gx在?∞,?1为增,在?1,+∞也为增,
而g?4=e?4?13<0,?g?3=e?3>0,
故?4
22.
【答案】
解:(1)?将C1的参数方程化为普通方程为(x?1)2+y2=3,
即x2+y2?2x?2=0,
∴ C1的极坐标方程为ρ2?2ρcosθ?2=0.
将C2的极坐标方程ρ=1化为直角坐标方程为x2+y2=1.
(2)将θ=π3(ρ≥0),代入C1:ρ2?2ρcosθ?2=0,
整理得ρ2?ρ?2=0,
解得:ρ1=2,即|OA|=2.
∵ 曲线C2是圆心在原点,半径为1的圆,
∴ 射线θ=π3(ρ≥0)与C2相交,则ρ2=1,即|OB|=1,
故|BA|=|ρ1?ρ2|=2?1=1.
【考点】
直线的极坐标方程
圆的参数方程
圆的极坐标方程
【解析】
(Ⅰ)?将C1的参数方程化为普通方程为(x?1)2+y2=3,即x2+y2?2x?2=0,利用互化公式可得:C1的极坐标方程.同理利用互化公式将C2的极坐标方程ρ=1化为直角坐标方程.
(Ⅱ)将θ=π3(ρ≥0),代入C1:ρ2?2ρcosθ?2=0.整理得ρ2?ρ?2=0,解得:ρ1,可得|OA|=ρ1.把射线θ=π3(ρ≥0)代入C2的方程,解得ρ2=1,即|OB|=ρ2.可得|BA|=|ρ1?ρ2|.
【解答】
解:(1)?将C1的参数方程化为普通方程为(x?1)2+y2=3,
即x2+y2?2x?2=0,
∴ C1的极坐标方程为ρ2?2ρcosθ?2=0.
将C2的极坐标方程ρ=1化为直角坐标方程为x2+y2=1.
(2)将θ=π3(ρ≥0),代入C1:ρ2?2ρcosθ?2=0,
整理得ρ2?ρ?2=0,
解得:ρ1=2,即|OA|=2.
∵ 曲线C2是圆心在原点,半径为1的圆,
∴ 射线θ=π3(ρ≥0)与C2相交,则ρ2=1,即|OB|=1,
故|BA|=|ρ1?ρ2|=2?1=1.
同课章节目录
