2.2 整式的加减(第三课时 整式的加减法则) 课件(共24张PPT)
文档属性
| 名称 | 2.2 整式的加减(第三课时 整式的加减法则) 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-01 10:43:43 | ||
图片预览








文档简介
2.2 整式的加减
第二章 整式的加减
第三课时 整式的加减运算法则
人教版 七上
去括号法则:
1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
去括号法则顺口溜:
1)括号外是“+”号,括号内符号不变。
2)括号外是“-” 号,括号内符号全变。
复习巩固
1、熟练进行整式的加减运算。
2、利用去括号法则会进行整式的化简。
重点
熟练进行整式的加减运算。
难点
利用去括号法则会进行整式的化简。
学习目标
(1)(2x-3y)+(5x+4y);
解:(2x-3y)+(5x+4y)
=2x-3y+5x+4y
=7x+y
合并同类项
去括号
计算两个多项式的和
例6 计算:(1)(2x-3y)+(5x+4y); (2)(8a-7b)-(4a-5b)
典例分析
(2)(8a-7b)-(4a-5b)
解:(8a-7b)-(4a-5b)
=8a-7b-4a+5b)
=4a-2b
合并同类项
去括号
计算两个多项式的差
例6 计算:(1)(2x-3y)+(5x+4y); (2)(8a-7b)-(4a-5b)
解:
有括号要先去括号
有同类项再合并同类项
结果中不能再有同类项
求多项式 与 的和。
针对练习
求多项式 与 的差。
解:
有括号要先去括号,注意变号
有同类项再合并同类项
结果中不能再有同类项
(4-5????2+3x)-(-2x +7????2-3)
?
=4-5????2+3x + 2x -7????2+3
?
=(-5????2-7????2?)+(3x-2x)+(4+3)
?
=-12????2+5????+7
?
针对练习
3)运算结果,常将多项式的某个字母(如x)的降幂(升幂)排列.
1)几个整式相加减,通常用括号把每一个整式括起来,再用加、减连接,然后进行运算.
2)整式加减实际上就是:去括号、合并同类项.
归纳小结
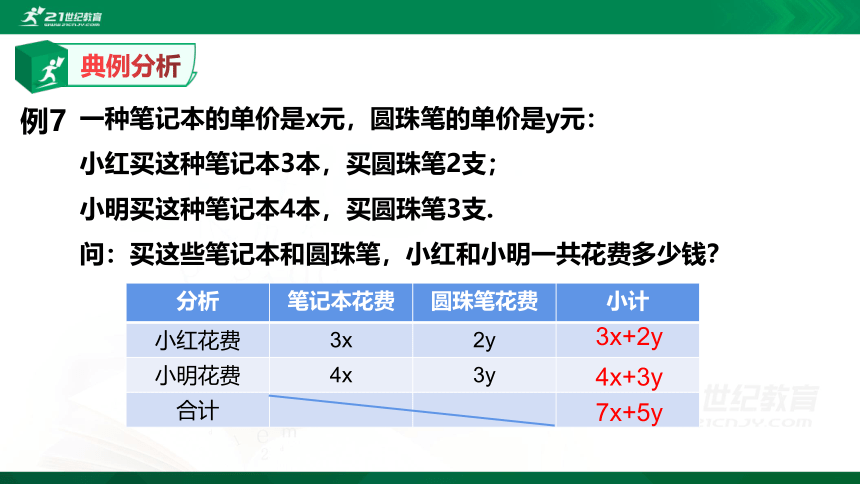
一种笔记本的单价是x元,圆珠笔的单价是y元:
小红买这种笔记本3本,买圆珠笔2支;
小明买这种笔记本4本,买圆珠笔3支.
问:买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}分析
笔记本花费
圆珠笔花费
小计
小红花费
3x
2y
小明花费
4x
3y
合计
3x+2y
4x+3y
7x+5y
例7
典例分析
一种笔记本的单价是x元,圆珠笔的单价是y元:
小红买这种笔记本3本,买圆珠笔2支;
小明买这种笔记本4本,买圆珠笔3支.
问:买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}分析
笔记本花费
圆珠笔花费
合计
小红花费
3x
2y
小明花费
4x
3y
小计
3x+4x
2y+3y
7x+5y
大客车上原有(3a-b)人,中途下车一半人,又上车若干人,此时车上共有乘客(8a-5b)人,则上车乘客有多少人?当a=10,b=8时,上车乘客有多少人?
解:由题意得,8a-5b-?????????????????=????????????????-????????????,所以上车乘客为(????????????????-????????????)
当a=10,b=8时,上车乘客为29人.
?
针对练习
例8 做大小两个长方体纸盒,尺寸如下(单位:cm):
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
长
宽
高
小纸盒
a
b
c
大纸盒
1.5a
2b
2c
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比小纸盒多用料多少平方厘米?
典例分析
解:小纸盒的表面积是(2ab+2bc+2ca)cm2
大纸盒的表面积是( 6ab+8bc+6ca)cm2
(1)做这两个纸盒共用料
(2ab+2bc+2ca)+(6ab+8bc+6ca)
=2ab+2bc+2ca+6ab+8bc+6ca
=8ab+10bc+8ca
例8 做大小两个长方体纸盒,尺寸如下(单位:cm):
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
长
宽
高
小纸盒
a
b
c
大纸盒
1.5a
2b
2c
(2)做大纸盒比小纸盒多用料多少平方厘米?
解:小纸盒的表面积是(2ab+2bc+2ca)cm2
大纸盒的表面积是( 6ab+8bc+6ca)cm2
(2)做大纸盒比做小纸盒多用料
(6ab+8bc+6ca)-(2ab+2bc+2ca)
=6ab+8bc+6ca-2ab-2bc-2ca
=4ab+6bc+4ca
1.如果用a,b分别表示一个两位数的十位数字和个位数字,
那么这个两位数可以表示为____________________。
交换这个两位数的十位数字和个位数字,得到的新数是 。
1)将这两个数相加得: ____________________。
2)将这两个数相减得: ____________________。
10b+a
10a+b
11a+11b
9a-9b
针对练习
2.(1)化简求值: 2(x2y+xy)-3(x2y-xy)-4x2y,其中x=-1,y=????????.
(2)解答:老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下: +(-3x2+5x-7)=-2x2+3x-6.求所捂的多项式.
?
(1)原式=2????2????+2?????????3????2????+3?????????4????2???? =-5x2y+5xy;
当x=-1,y= 12 时,原式=?5×?12×12+5×?1×12=-5.
(2)原式=(-2x2+3x-6)-(-3x2+5x-7)
=-2x2+3x-6+3x2-5x+7
=x2-2x+1,
即所捂的多项式是x2-2x+1.
?
3.如图,把四张大小相同的长方形卡片(如图①)按图2、图③两种方式放在一个底面为长方形(长比宽多5cm)的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为C1,图3中阴影部分的周长为C2,那么C1比C2大_____cm.
解:设小长方形的长为acm,宽为bcm,大长方形的宽为xcm,长为(x+5)cm,
∴②阴影周长为:2(x+5+x)=4x+10,
∴③下面的周长为:2(x﹣2b+x+5﹣2b),
上面的总周长为:2(x+5﹣a+x﹣a),
∴总周长为:2(x﹣2b+x+5﹣2b)+2(x+5﹣a+x﹣a)=4(x+5)+4x﹣4(a+2b),
又∵a+2b=x+5,∴4(x+5)+4x﹣4(a+2b)=4x,
∴C1﹣C2=4x+10﹣4x=10(cm),
1. 化简x+y-(x-y)的最后结果是( )
A. 2x+2y B. 2y C. 2x D. 0
B
2.多项式3a2-6a+4与4a2+5a-3的差是( )
A.-a2-11a+7
B.-a2-a+1
C.a2+11a-7
D.a2-a+1
A
课堂练习
3. 一个多项式加上3y2-2y-5得到多项式5y3-4y-6,则原来的多项式为( )
A. 5y3+3y2+2y-1 B. 5y3-3y2-2y-6
C. 5y3 +3y2-2y-1 D. 5y3-3y2-2y-1
D
4.先化简,再求值:
其中
解:
当 时,
原式=
5.计算:
(1)2(x+3x2+1)-3(2x2-x+2);
(2)(4a2-3b2)-[2(a2-1)+2b2-3].
解:原式=2a2-5b2+5
解:原式=5x-4
6. 已知A=2x2+3ax-2x-1,B=-x2+ax-1,且3A+6B的值不含x项,求a的值.
解:3A+6B=3(2x2+3ax-2x-1)+6(-x2+ax-1)
=6x2+9ax-6x-3-6x2+6ax-6
=15ax-6x-9=(15a-6)x-9,
因为3A+6B中不含x项,即x项的系数为零,
所以15a-6=0,a=????????.
?
整式的加减
整式的加减运算
整式加减的应用
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
课堂小结
第二章 整式的加减
第三课时 整式的加减运算法则
人教版 七上
去括号法则:
1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
去括号法则顺口溜:
1)括号外是“+”号,括号内符号不变。
2)括号外是“-” 号,括号内符号全变。
复习巩固
1、熟练进行整式的加减运算。
2、利用去括号法则会进行整式的化简。
重点
熟练进行整式的加减运算。
难点
利用去括号法则会进行整式的化简。
学习目标
(1)(2x-3y)+(5x+4y);
解:(2x-3y)+(5x+4y)
=2x-3y+5x+4y
=7x+y
合并同类项
去括号
计算两个多项式的和
例6 计算:(1)(2x-3y)+(5x+4y); (2)(8a-7b)-(4a-5b)
典例分析
(2)(8a-7b)-(4a-5b)
解:(8a-7b)-(4a-5b)
=8a-7b-4a+5b)
=4a-2b
合并同类项
去括号
计算两个多项式的差
例6 计算:(1)(2x-3y)+(5x+4y); (2)(8a-7b)-(4a-5b)
解:
有括号要先去括号
有同类项再合并同类项
结果中不能再有同类项
求多项式 与 的和。
针对练习
求多项式 与 的差。
解:
有括号要先去括号,注意变号
有同类项再合并同类项
结果中不能再有同类项
(4-5????2+3x)-(-2x +7????2-3)
?
=4-5????2+3x + 2x -7????2+3
?
=(-5????2-7????2?)+(3x-2x)+(4+3)
?
=-12????2+5????+7
?
针对练习
3)运算结果,常将多项式的某个字母(如x)的降幂(升幂)排列.
1)几个整式相加减,通常用括号把每一个整式括起来,再用加、减连接,然后进行运算.
2)整式加减实际上就是:去括号、合并同类项.
归纳小结
一种笔记本的单价是x元,圆珠笔的单价是y元:
小红买这种笔记本3本,买圆珠笔2支;
小明买这种笔记本4本,买圆珠笔3支.
问:买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}分析
笔记本花费
圆珠笔花费
小计
小红花费
3x
2y
小明花费
4x
3y
合计
3x+2y
4x+3y
7x+5y
例7
典例分析
一种笔记本的单价是x元,圆珠笔的单价是y元:
小红买这种笔记本3本,买圆珠笔2支;
小明买这种笔记本4本,买圆珠笔3支.
问:买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}分析
笔记本花费
圆珠笔花费
合计
小红花费
3x
2y
小明花费
4x
3y
小计
3x+4x
2y+3y
7x+5y
大客车上原有(3a-b)人,中途下车一半人,又上车若干人,此时车上共有乘客(8a-5b)人,则上车乘客有多少人?当a=10,b=8时,上车乘客有多少人?
解:由题意得,8a-5b-?????????????????=????????????????-????????????,所以上车乘客为(????????????????-????????????)
当a=10,b=8时,上车乘客为29人.
?
针对练习
例8 做大小两个长方体纸盒,尺寸如下(单位:cm):
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
长
宽
高
小纸盒
a
b
c
大纸盒
1.5a
2b
2c
(1)做这两个纸盒共用料多少平方厘米?
(2)做大纸盒比小纸盒多用料多少平方厘米?
典例分析
解:小纸盒的表面积是(2ab+2bc+2ca)cm2
大纸盒的表面积是( 6ab+8bc+6ca)cm2
(1)做这两个纸盒共用料
(2ab+2bc+2ca)+(6ab+8bc+6ca)
=2ab+2bc+2ca+6ab+8bc+6ca
=8ab+10bc+8ca
例8 做大小两个长方体纸盒,尺寸如下(单位:cm):
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
长
宽
高
小纸盒
a
b
c
大纸盒
1.5a
2b
2c
(2)做大纸盒比小纸盒多用料多少平方厘米?
解:小纸盒的表面积是(2ab+2bc+2ca)cm2
大纸盒的表面积是( 6ab+8bc+6ca)cm2
(2)做大纸盒比做小纸盒多用料
(6ab+8bc+6ca)-(2ab+2bc+2ca)
=6ab+8bc+6ca-2ab-2bc-2ca
=4ab+6bc+4ca
1.如果用a,b分别表示一个两位数的十位数字和个位数字,
那么这个两位数可以表示为____________________。
交换这个两位数的十位数字和个位数字,得到的新数是 。
1)将这两个数相加得: ____________________。
2)将这两个数相减得: ____________________。
10b+a
10a+b
11a+11b
9a-9b
针对练习
2.(1)化简求值: 2(x2y+xy)-3(x2y-xy)-4x2y,其中x=-1,y=????????.
(2)解答:老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下: +(-3x2+5x-7)=-2x2+3x-6.求所捂的多项式.
?
(1)原式=2????2????+2?????????3????2????+3?????????4????2???? =-5x2y+5xy;
当x=-1,y= 12 时,原式=?5×?12×12+5×?1×12=-5.
(2)原式=(-2x2+3x-6)-(-3x2+5x-7)
=-2x2+3x-6+3x2-5x+7
=x2-2x+1,
即所捂的多项式是x2-2x+1.
?
3.如图,把四张大小相同的长方形卡片(如图①)按图2、图③两种方式放在一个底面为长方形(长比宽多5cm)的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长为C1,图3中阴影部分的周长为C2,那么C1比C2大_____cm.
解:设小长方形的长为acm,宽为bcm,大长方形的宽为xcm,长为(x+5)cm,
∴②阴影周长为:2(x+5+x)=4x+10,
∴③下面的周长为:2(x﹣2b+x+5﹣2b),
上面的总周长为:2(x+5﹣a+x﹣a),
∴总周长为:2(x﹣2b+x+5﹣2b)+2(x+5﹣a+x﹣a)=4(x+5)+4x﹣4(a+2b),
又∵a+2b=x+5,∴4(x+5)+4x﹣4(a+2b)=4x,
∴C1﹣C2=4x+10﹣4x=10(cm),
1. 化简x+y-(x-y)的最后结果是( )
A. 2x+2y B. 2y C. 2x D. 0
B
2.多项式3a2-6a+4与4a2+5a-3的差是( )
A.-a2-11a+7
B.-a2-a+1
C.a2+11a-7
D.a2-a+1
A
课堂练习
3. 一个多项式加上3y2-2y-5得到多项式5y3-4y-6,则原来的多项式为( )
A. 5y3+3y2+2y-1 B. 5y3-3y2-2y-6
C. 5y3 +3y2-2y-1 D. 5y3-3y2-2y-1
D
4.先化简,再求值:
其中
解:
当 时,
原式=
5.计算:
(1)2(x+3x2+1)-3(2x2-x+2);
(2)(4a2-3b2)-[2(a2-1)+2b2-3].
解:原式=2a2-5b2+5
解:原式=5x-4
6. 已知A=2x2+3ax-2x-1,B=-x2+ax-1,且3A+6B的值不含x项,求a的值.
解:3A+6B=3(2x2+3ax-2x-1)+6(-x2+ax-1)
=6x2+9ax-6x-3-6x2+6ax-6
=15ax-6x-9=(15a-6)x-9,
因为3A+6B中不含x项,即x项的系数为零,
所以15a-6=0,a=????????.
?
整式的加减
整式的加减运算
整式加减的应用
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
课堂小结
