人教版八年级数学上册13.3等腰三角形应用(讲义+答案)
文档属性
| 名称 | 人教版八年级数学上册13.3等腰三角形应用(讲义+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 45.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 08:24:00 | ||
图片预览




文档简介
等腰三角形应用(讲义)
课前预习
直角三角形全等的判定定理:_________________________.
线段垂直平分线上的点到_____________________________.
角平分线上的点到___________________________________.
已知:如图,线段AB的端点A在直线l上(AB与l不垂直),请在直线l上另找一点C,使△ABC是等腰三角形.这样的点能找几个?请你找出所有符合条件的点.
知识点睛
垂直平分线相关定理:
①________________________________________________;
②到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
已知:如图,PA=PB.
求证:点P在线段AB的垂直平分线上.
证明:
角平分线相关定理:
①________________________________________________;
②在一个角的内部,到角的两边距离相等的点在这个角的平分线上.
已知:如图,点P在∠AOB内部,PC⊥OA于点C,PD⊥OB于点D,且PC=PD.
求证:点P在∠AOB的平分线上.
证明:
在等腰三角形中,_________________,________________,______________重合(也称“__________”),这是等腰三角形的重要性质.若在一个三角形中,当中线,高线,角平分线“三线”中有“两线”重合时,则尝试构造___________.
精讲精练
已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC.
求证:直线AO垂直平分线段BC.
如图,已知PA⊥OM于A,PB⊥ON于B,且PA=PB.
∠MON=50°,∠OPC=30°,求∠PCA的大小.
如图,已知BE平分∠ABC,CE平分∠ACD,且交BE于E.
求证:AE平分∠FAC.
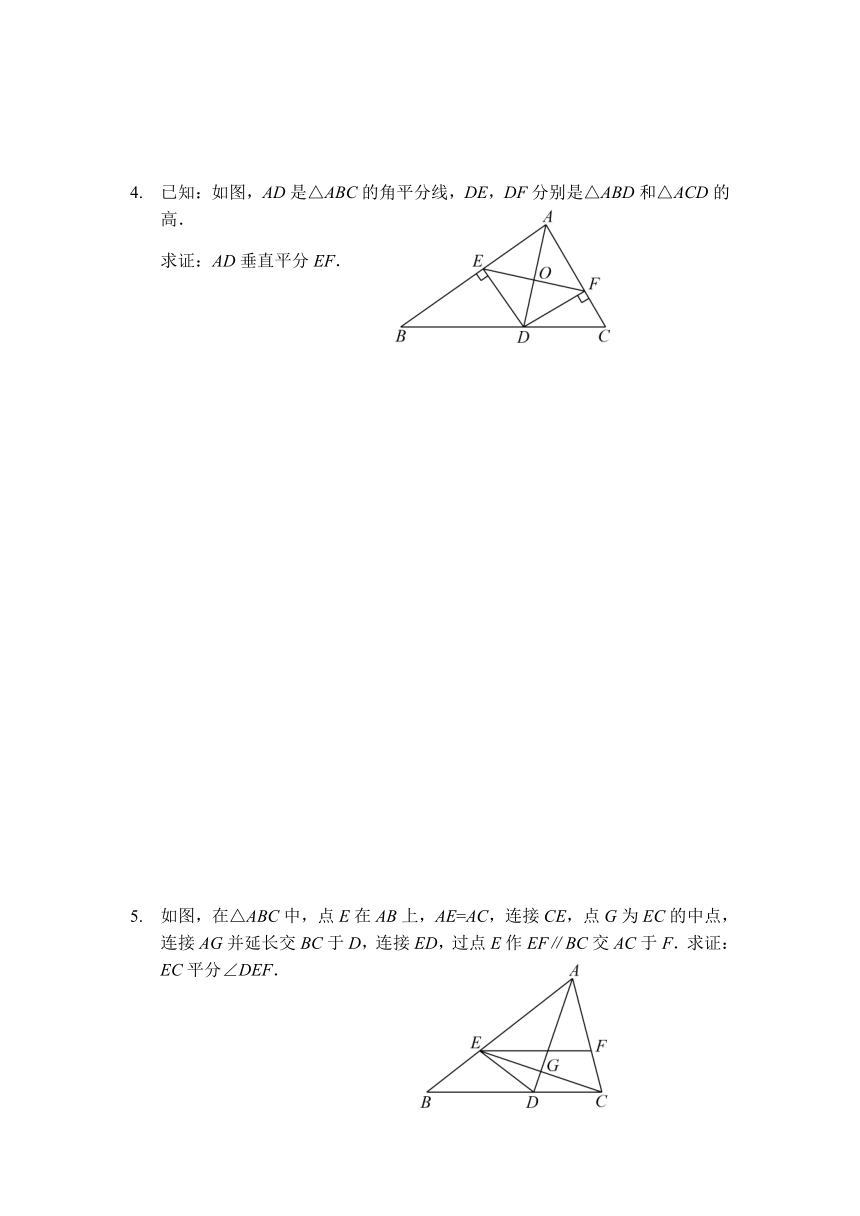
已知:如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.
求证:AD垂直平分EF.
如图,在△ABC中,点E在AB上,AE=AC,连接CE,点G为EC的中点,连接AG并延长交BC于D,连接ED,过点E作EF∥BC交AC于F.求证:EC平分∠DEF.
已知:如图,D,E分别是AB,AC的中点,CD⊥AB于D,BE⊥AC于E,CD,BE交于点O.
求证:AB=AC.
已知:如图,在△ABC中,∠A=90°,AB=AC,BD平分∠ABC,CE⊥BD交BD的延长线于E,若CE=5
cm,求BD的长.
如图,在△ABC中,延长BC到D,使CD=AC,连接AD,CE平分∠ACB,交AB于E,且AE=BE.
求证:BC=CD.
在Rt△ABC中,∠C=90°,∠A=30°,若要在直线BC或AC上取一点P,使△ABP是等腰三角形,符合条件的点P有________个.
如图所示的正方形网格中,网格线的交点称为格点.已知A,B是两个格点,若点C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C有________个.
【参考答案】
课前预习
1.SAS,SSS,ASA,AAS,HL
2.这条线段的两个端点的距离相等
3.这个角的两边的距离相等
4.这样的点有4个
知识点睛
1.线段垂直平分线上的点到这条线段的两个端点的距离相等
2.角平分线上的点到这个角的两边距离相等
3.顶角的平分线
底边上的中线
底边上的高
三线合一
等腰三角形
精讲精练
证明略(提示:利用等腰三角形“三线合一”)
55°,证明略
证明略(提示:过点E作EM⊥BF于M,EN⊥BD于N,EP⊥AC于P,证EP=EM)
证明略(提示:利用等腰△DEF“三线合一”,证明AD垂直平分EF)
证明略
证明略(提示:连接BC,证△ABC是等边三角形)
BD=10
cm(提示:延长BA交CE的延长线于F,先证△BCF是等腰三角形,再证△ADB≌△AFC)
证明略(提示:过点E作EF⊥AC于F,EG⊥BC于G,证明
△ABC是等腰三角形)
6个,作图略(两圆一线)
8个,作图略(两圆一线)
课前预习
直角三角形全等的判定定理:_________________________.
线段垂直平分线上的点到_____________________________.
角平分线上的点到___________________________________.
已知:如图,线段AB的端点A在直线l上(AB与l不垂直),请在直线l上另找一点C,使△ABC是等腰三角形.这样的点能找几个?请你找出所有符合条件的点.
知识点睛
垂直平分线相关定理:
①________________________________________________;
②到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
已知:如图,PA=PB.
求证:点P在线段AB的垂直平分线上.
证明:
角平分线相关定理:
①________________________________________________;
②在一个角的内部,到角的两边距离相等的点在这个角的平分线上.
已知:如图,点P在∠AOB内部,PC⊥OA于点C,PD⊥OB于点D,且PC=PD.
求证:点P在∠AOB的平分线上.
证明:
在等腰三角形中,_________________,________________,______________重合(也称“__________”),这是等腰三角形的重要性质.若在一个三角形中,当中线,高线,角平分线“三线”中有“两线”重合时,则尝试构造___________.
精讲精练
已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC.
求证:直线AO垂直平分线段BC.
如图,已知PA⊥OM于A,PB⊥ON于B,且PA=PB.
∠MON=50°,∠OPC=30°,求∠PCA的大小.
如图,已知BE平分∠ABC,CE平分∠ACD,且交BE于E.
求证:AE平分∠FAC.
已知:如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高.
求证:AD垂直平分EF.
如图,在△ABC中,点E在AB上,AE=AC,连接CE,点G为EC的中点,连接AG并延长交BC于D,连接ED,过点E作EF∥BC交AC于F.求证:EC平分∠DEF.
已知:如图,D,E分别是AB,AC的中点,CD⊥AB于D,BE⊥AC于E,CD,BE交于点O.
求证:AB=AC.
已知:如图,在△ABC中,∠A=90°,AB=AC,BD平分∠ABC,CE⊥BD交BD的延长线于E,若CE=5
cm,求BD的长.
如图,在△ABC中,延长BC到D,使CD=AC,连接AD,CE平分∠ACB,交AB于E,且AE=BE.
求证:BC=CD.
在Rt△ABC中,∠C=90°,∠A=30°,若要在直线BC或AC上取一点P,使△ABP是等腰三角形,符合条件的点P有________个.
如图所示的正方形网格中,网格线的交点称为格点.已知A,B是两个格点,若点C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C有________个.
【参考答案】
课前预习
1.SAS,SSS,ASA,AAS,HL
2.这条线段的两个端点的距离相等
3.这个角的两边的距离相等
4.这样的点有4个
知识点睛
1.线段垂直平分线上的点到这条线段的两个端点的距离相等
2.角平分线上的点到这个角的两边距离相等
3.顶角的平分线
底边上的中线
底边上的高
三线合一
等腰三角形
精讲精练
证明略(提示:利用等腰三角形“三线合一”)
55°,证明略
证明略(提示:过点E作EM⊥BF于M,EN⊥BD于N,EP⊥AC于P,证EP=EM)
证明略(提示:利用等腰△DEF“三线合一”,证明AD垂直平分EF)
证明略
证明略(提示:连接BC,证△ABC是等边三角形)
BD=10
cm(提示:延长BA交CE的延长线于F,先证△BCF是等腰三角形,再证△ADB≌△AFC)
证明略(提示:过点E作EF⊥AC于F,EG⊥BC于G,证明
△ABC是等腰三角形)
6个,作图略(两圆一线)
8个,作图略(两圆一线)
