人教版数学九年级上册:24.2.1 点和圆的位置关系 课件(共47张PPT)
文档属性
| 名称 | 人教版数学九年级上册:24.2.1 点和圆的位置关系 课件(共47张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 00:00:00 | ||
图片预览







文档简介
(共47张PPT)
课例分析
24.2.1
点和圆的位置关系
教学目标
了解点和圆的位置关系关注数形之间的转化;
过一点、过两点可以作无数个圆,并熟知圆心分布;
不在同一条直线上的三个点确定一个圆;
三角形的外接圆;圆的内接三角形;外心;
结合“过同一条直线上的三点不能作圆”介绍反证法.
教学重点难点
教学重点:
点和圆的位置关系;
定理不在同一条直线上的三个点确定一个圆.
教学难点:
过一点、过两点可以作无数个圆的圆心分布;
反证法.
五个环节
实际引入
1
探究新知
2
巩固提升
3
深入探究
4
小结反思
5
下图是一位射击运动员,六发子弹在射击靶上留下的痕迹.
一、实际引入
射击靶由许多同心圆构成的,这些圆的圆心相同,半径不同.你知道击中靶的不同位置的成绩是如何计算的吗?
一、实际引入
一、实际引入
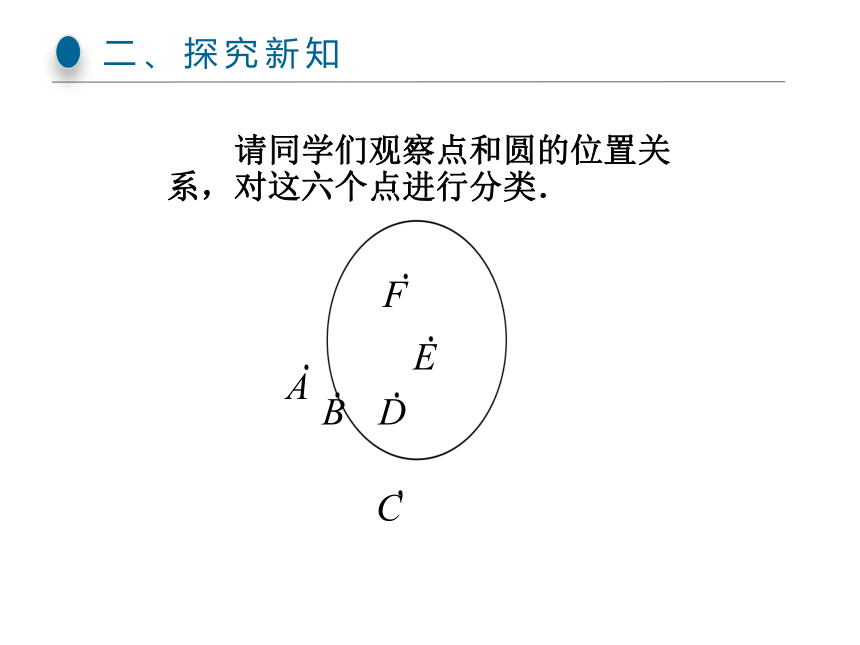
请同学们观察点和圆的位置关系,对这六个点进行分类.
C
A
B
D
E
F
二、探究新知
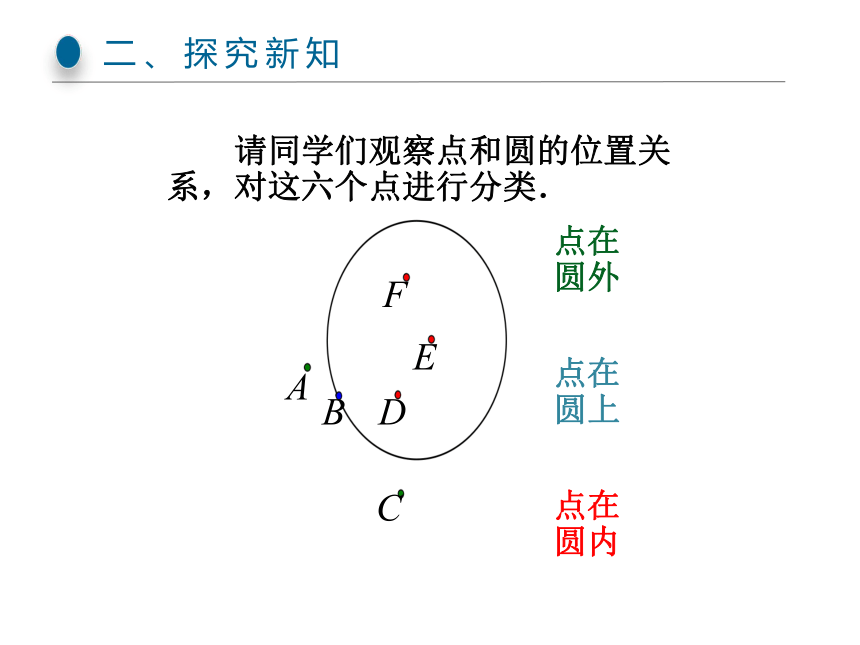
请同学们观察点和圆的位置关系,对这六个点进行分类.
点在圆外
点在圆上
点在圆内
C
A
B
D
E
F
二、探究新知
点和圆的位置关系的几何特征、代数特征.
点在圆外
点在圆上
点在圆内
点到圆心的距离等于半径
点到圆心的距离大于半径
点到圆心的距离小于半径
C
A
B
D
E
F
r
O
二、探究新知
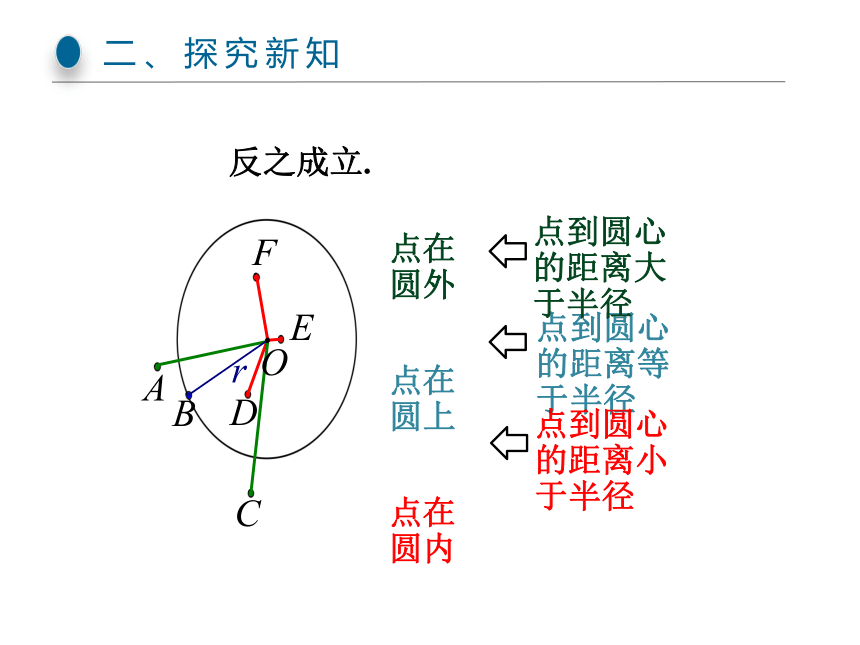
反之成立.
点在圆外
点在圆上
点在圆内
点到圆心的距离等于半径
点到圆心的距离大于半径
点到圆心的距离小于半径
C
A
B
D
E
F
r
O
二、探究新知
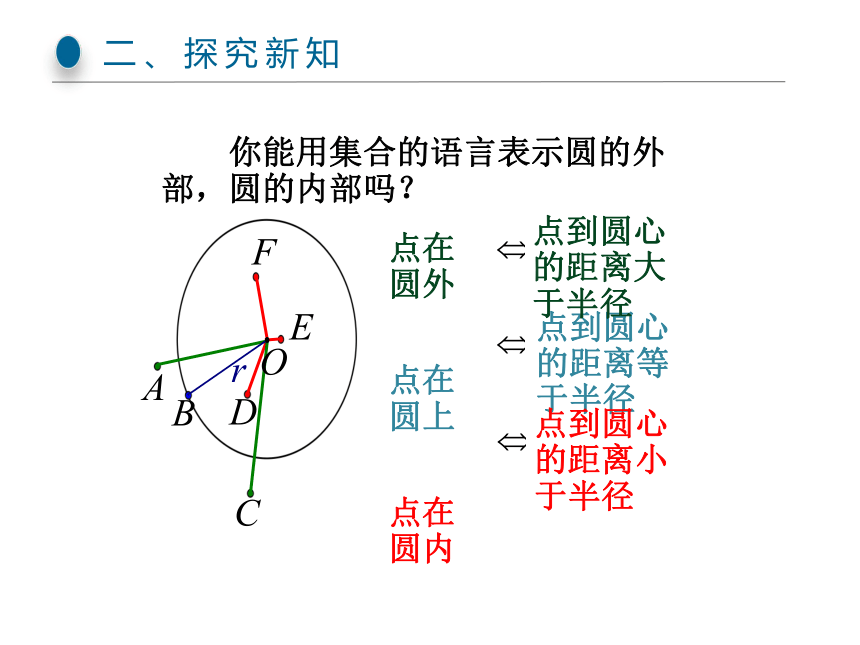
你能用集合的语言表示圆的外部,圆的内部吗?
点在圆外
点在圆上
点在圆内
点到圆心的距离等于半径
点到圆心的距离大于半径
点到圆心的距离小于半径
C
A
B
D
E
F
r
O
二、探究新知
点和圆的位置关系
设⊙O
的半径为
r,点
P
到圆心的距离为
d,则有:
点
P
在圆外 d>r
;
点
P
在圆上 d=r
;
点
P
在圆内 d<r
.
基本概念
二、探究新知
巩固练习
1.
画出由所有到已知点O的距离大于或等于2
cm,
并且小于或等于3
cm的点组成的图形.
3
cm
2
cm
o
三、巩固提升
弹着点与靶心的距离决定了它在哪个圆内,弹着点离靶心越近,它所在的区域就越靠内,对应的环数也就越高,射击成绩越好.
三、巩固提升
巩固练习
2.
体育课上,小明和小丽的铅球成绩分别是6.4
m和
5.1
m
,他们投出的铅球分别落在图中哪个区域内?
小丽
小明
三、巩固提升
3.
已知⊙O的面积为25π:
(1)若PO=5.5,则点P在
;
(2)若PO=4,则点P在
;
(3)若PO=
,则点P在圆上;
(4)若点P不在圆外,则PO__________.
圆外
圆内
5
≤5
巩固练习
三、巩固提升
4.
如图,已知矩形ABCD的边AB=3
cm,AD=4
cm.
A
D
C
B
(1)以点A为圆心,3
cm为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆上,D在圆外,C在圆外)
巩固练习
三、巩固提升
(2)以点A为圆心,4
cm为半径作圆A,则点B、C、D与圆A的位置关系如何?
4.
如图,已知矩形ABCD的边AB=3
cm,AD=4
cm.
(B在圆内,D在圆上,C在圆外)
A
D
C
B
巩固练习
三、巩固提升
(3)以点A为圆心,5
cm为半径作圆A,则点B、C、D与圆A的位置关系如何?
4.
如图,已知矩形ABCD的边AB=3
cm,AD=4
cm.
(B在圆内,D在圆内,C在圆上)
A
D
C
B
巩固练习
三、巩固提升
类比探究
几点确定一个圆?
两点确定一条直线.
四、深入探究
探究“过已知点作圆”
我们知道,已知圆心和半径,可以作一个圆.经过一个已知点A能不能作圆,这样的圆你能作出多少个?经过两个已知点A,B能不能作圆?如果能,圆心分布有什么特点?
四、深入探究
圆心为这个点以外任意一点.
经过一个已知点
A
作圆.
A
探究“过已知点作圆”
结论:
过一点可以画无数个圆.
四、深入探究
经过两个已知点
A,B作圆.
A
B
圆心在两点所连线段的垂直平分线上.
结论:
过两点可以画无数个圆.
探究“过已知点作圆”
四、深入探究
经过三个已知点
A,B,C作圆.
探究“过已知点作圆”
四、深入探究
活动
请同学们画三个点
A,B,C.
A
B
C
A
B
C
四、深入探究
思考
经过不在同一条直线上的三个点
A,B,C能不能作圆?如果能,如何确定所作圆的圆心?
A
B
C
四、深入探究
思考
O
A
B
C
D
E
F
G
经过不在同一条直线上的三个点
A,B,C能不能作圆?如果能,如何确定所作圆的圆心?
四、深入探究
不在同一条直线上的三个点确定一个圆.
O
A
B
C
D
E
F
G
四、深入探究
概念
三角形的外接圆;圆的内接三角形;外心.
A
B
C
O
外心是三角形三边的垂直平分线的交点;
外心到三角形顶点的距离相等.
四、深入探究
●O
A
B
C
C
A
B
┐
●O
●O
三角形内
试一试
A
B
C
请作出锐角三角形、直角三角形、钝角三角形的外接圆.这些外接圆的圆心在什么位置?
斜边中点
三角形外
四、深入探究
巩固练习
5.
如图,CD所在的直线垂直平分线段AB,怎么用这样的工具找到圆形工件的圆心?
O
四、深入探究
6.
小腾家的圆形镜子损坏了,他要定制一个大小相同的新镜子,如何测量镜子的半径?
A
B
C
O
巩固练习
四、深入探究
7.
已知,Rt△ABC中,若∠C=90°,AC=5
cm,BC=12
cm,求△ABC的外接圆半径.
解:
根据勾股定理得,
直角三角形的外心在斜边的中点,
斜边就是直径,
巩固练习
所以△ABC的外接圆半径为
6.5
cm.
四、深入探究
思考
经过同一条直线上的三个点
A,B,C能作出一个圆吗?如何证明你的结论?
A
B
C
l1
l2
四、深入探究
证明
经过同一条直线上的三点不能作圆.
A
B
C
l1
l2
P
l
四、深入探究
假设命题的结论不成立,经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立,这种方法叫做反证法.
四、深入探究
巩固练习
8.
判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆(
).
(2)任意一个圆有且只有一个内接三角形(
)
(3)经过三点一定可以确定一个圆(
)
(4)三角形的外心到三角形各顶点的距离相等(
)
√
×
×
√
四、深入探究
9.
若一个三角形的外心在一边上,则此三角形的形状为(
)
A、锐角三角形
B、直角三角形
C、钝角三角形
D、等边三角形
B
巩固练习
四、深入探究
课堂小结
点和圆的位置关系
设⊙O
的半径为
r,点
P1
,
P2
,
P3到圆心的距离为
d1,d2,d3,则有:
点
P1
在圆外
d1>r
;
点
P2在圆上
d2=r
;
点
P3
在圆内
d3<r
.
d1
·
P1
·
P2
·
P3
d2
d3
五、小结反思
过已知点作圆
A
过一点,过两点可以画无数个圆.
A
B
五、小结反思
课堂小结
不在同一条直线上的三个点确定一个圆.
三角形的外接圆;圆的内接三角形;外心.
假设命题的结论不成立,经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立,这种方法叫做反证法.
五、小结反思
课堂小结
课后作业
1.
⊙O
的半径为10
cm,根据下列点
P
到圆心
O
的距离,判断点
P
和⊙O
的位置关系:
(1)8
cm;
(2)10
cm;
(3)12
cm.
2.
⊙O
的半径
6,当OP=6时,点P在
;当OP
时点P在圆内;当OP
时,点
P
不在圆外.
五、小结反思
课后作业
3.
已知
AB
=6
cm,画半径为4
cm的圆,使它经过A,B
两点.
这样的圆能画出多少个?如果半径为3
cm,2
cm呢?
4.
如图,分别作出锐角三角形、直角三角形和钝角三角形的外接圆,它们外心的位置有什么特点?
五、小结反思
5.
如图是一名考古学家发现的一块古代车轮的碎片,你能帮他找出这个轮子的半径吗?说出你的理由.
A
B
C
O
五、小结反思
课后作业
试一试
请用反证法证明“两直线平行,同位角相等”.
已知:AB∥CD,
求证:∠1=∠2.
A
B
C
D
E
F
A’
B’
1
2
O
五、小结反思
思考
经过任意四个点是不是可以作一个圆?
五、小结反思
课例分析
24.2.1
点和圆的位置关系
教学目标
了解点和圆的位置关系关注数形之间的转化;
过一点、过两点可以作无数个圆,并熟知圆心分布;
不在同一条直线上的三个点确定一个圆;
三角形的外接圆;圆的内接三角形;外心;
结合“过同一条直线上的三点不能作圆”介绍反证法.
教学重点难点
教学重点:
点和圆的位置关系;
定理不在同一条直线上的三个点确定一个圆.
教学难点:
过一点、过两点可以作无数个圆的圆心分布;
反证法.
五个环节
实际引入
1
探究新知
2
巩固提升
3
深入探究
4
小结反思
5
下图是一位射击运动员,六发子弹在射击靶上留下的痕迹.
一、实际引入
射击靶由许多同心圆构成的,这些圆的圆心相同,半径不同.你知道击中靶的不同位置的成绩是如何计算的吗?
一、实际引入
一、实际引入
请同学们观察点和圆的位置关系,对这六个点进行分类.
C
A
B
D
E
F
二、探究新知
请同学们观察点和圆的位置关系,对这六个点进行分类.
点在圆外
点在圆上
点在圆内
C
A
B
D
E
F
二、探究新知
点和圆的位置关系的几何特征、代数特征.
点在圆外
点在圆上
点在圆内
点到圆心的距离等于半径
点到圆心的距离大于半径
点到圆心的距离小于半径
C
A
B
D
E
F
r
O
二、探究新知
反之成立.
点在圆外
点在圆上
点在圆内
点到圆心的距离等于半径
点到圆心的距离大于半径
点到圆心的距离小于半径
C
A
B
D
E
F
r
O
二、探究新知
你能用集合的语言表示圆的外部,圆的内部吗?
点在圆外
点在圆上
点在圆内
点到圆心的距离等于半径
点到圆心的距离大于半径
点到圆心的距离小于半径
C
A
B
D
E
F
r
O
二、探究新知
点和圆的位置关系
设⊙O
的半径为
r,点
P
到圆心的距离为
d,则有:
点
P
在圆外 d>r
;
点
P
在圆上 d=r
;
点
P
在圆内 d<r
.
基本概念
二、探究新知
巩固练习
1.
画出由所有到已知点O的距离大于或等于2
cm,
并且小于或等于3
cm的点组成的图形.
3
cm
2
cm
o
三、巩固提升
弹着点与靶心的距离决定了它在哪个圆内,弹着点离靶心越近,它所在的区域就越靠内,对应的环数也就越高,射击成绩越好.
三、巩固提升
巩固练习
2.
体育课上,小明和小丽的铅球成绩分别是6.4
m和
5.1
m
,他们投出的铅球分别落在图中哪个区域内?
小丽
小明
三、巩固提升
3.
已知⊙O的面积为25π:
(1)若PO=5.5,则点P在
;
(2)若PO=4,则点P在
;
(3)若PO=
,则点P在圆上;
(4)若点P不在圆外,则PO__________.
圆外
圆内
5
≤5
巩固练习
三、巩固提升
4.
如图,已知矩形ABCD的边AB=3
cm,AD=4
cm.
A
D
C
B
(1)以点A为圆心,3
cm为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆上,D在圆外,C在圆外)
巩固练习
三、巩固提升
(2)以点A为圆心,4
cm为半径作圆A,则点B、C、D与圆A的位置关系如何?
4.
如图,已知矩形ABCD的边AB=3
cm,AD=4
cm.
(B在圆内,D在圆上,C在圆外)
A
D
C
B
巩固练习
三、巩固提升
(3)以点A为圆心,5
cm为半径作圆A,则点B、C、D与圆A的位置关系如何?
4.
如图,已知矩形ABCD的边AB=3
cm,AD=4
cm.
(B在圆内,D在圆内,C在圆上)
A
D
C
B
巩固练习
三、巩固提升
类比探究
几点确定一个圆?
两点确定一条直线.
四、深入探究
探究“过已知点作圆”
我们知道,已知圆心和半径,可以作一个圆.经过一个已知点A能不能作圆,这样的圆你能作出多少个?经过两个已知点A,B能不能作圆?如果能,圆心分布有什么特点?
四、深入探究
圆心为这个点以外任意一点.
经过一个已知点
A
作圆.
A
探究“过已知点作圆”
结论:
过一点可以画无数个圆.
四、深入探究
经过两个已知点
A,B作圆.
A
B
圆心在两点所连线段的垂直平分线上.
结论:
过两点可以画无数个圆.
探究“过已知点作圆”
四、深入探究
经过三个已知点
A,B,C作圆.
探究“过已知点作圆”
四、深入探究
活动
请同学们画三个点
A,B,C.
A
B
C
A
B
C
四、深入探究
思考
经过不在同一条直线上的三个点
A,B,C能不能作圆?如果能,如何确定所作圆的圆心?
A
B
C
四、深入探究
思考
O
A
B
C
D
E
F
G
经过不在同一条直线上的三个点
A,B,C能不能作圆?如果能,如何确定所作圆的圆心?
四、深入探究
不在同一条直线上的三个点确定一个圆.
O
A
B
C
D
E
F
G
四、深入探究
概念
三角形的外接圆;圆的内接三角形;外心.
A
B
C
O
外心是三角形三边的垂直平分线的交点;
外心到三角形顶点的距离相等.
四、深入探究
●O
A
B
C
C
A
B
┐
●O
●O
三角形内
试一试
A
B
C
请作出锐角三角形、直角三角形、钝角三角形的外接圆.这些外接圆的圆心在什么位置?
斜边中点
三角形外
四、深入探究
巩固练习
5.
如图,CD所在的直线垂直平分线段AB,怎么用这样的工具找到圆形工件的圆心?
O
四、深入探究
6.
小腾家的圆形镜子损坏了,他要定制一个大小相同的新镜子,如何测量镜子的半径?
A
B
C
O
巩固练习
四、深入探究
7.
已知,Rt△ABC中,若∠C=90°,AC=5
cm,BC=12
cm,求△ABC的外接圆半径.
解:
根据勾股定理得,
直角三角形的外心在斜边的中点,
斜边就是直径,
巩固练习
所以△ABC的外接圆半径为
6.5
cm.
四、深入探究
思考
经过同一条直线上的三个点
A,B,C能作出一个圆吗?如何证明你的结论?
A
B
C
l1
l2
四、深入探究
证明
经过同一条直线上的三点不能作圆.
A
B
C
l1
l2
P
l
四、深入探究
假设命题的结论不成立,经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立,这种方法叫做反证法.
四、深入探究
巩固练习
8.
判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆(
).
(2)任意一个圆有且只有一个内接三角形(
)
(3)经过三点一定可以确定一个圆(
)
(4)三角形的外心到三角形各顶点的距离相等(
)
√
×
×
√
四、深入探究
9.
若一个三角形的外心在一边上,则此三角形的形状为(
)
A、锐角三角形
B、直角三角形
C、钝角三角形
D、等边三角形
B
巩固练习
四、深入探究
课堂小结
点和圆的位置关系
设⊙O
的半径为
r,点
P1
,
P2
,
P3到圆心的距离为
d1,d2,d3,则有:
点
P1
在圆外
d1>r
;
点
P2在圆上
d2=r
;
点
P3
在圆内
d3<r
.
d1
·
P1
·
P2
·
P3
d2
d3
五、小结反思
过已知点作圆
A
过一点,过两点可以画无数个圆.
A
B
五、小结反思
课堂小结
不在同一条直线上的三个点确定一个圆.
三角形的外接圆;圆的内接三角形;外心.
假设命题的结论不成立,经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到原命题成立,这种方法叫做反证法.
五、小结反思
课堂小结
课后作业
1.
⊙O
的半径为10
cm,根据下列点
P
到圆心
O
的距离,判断点
P
和⊙O
的位置关系:
(1)8
cm;
(2)10
cm;
(3)12
cm.
2.
⊙O
的半径
6,当OP=6时,点P在
;当OP
时点P在圆内;当OP
时,点
P
不在圆外.
五、小结反思
课后作业
3.
已知
AB
=6
cm,画半径为4
cm的圆,使它经过A,B
两点.
这样的圆能画出多少个?如果半径为3
cm,2
cm呢?
4.
如图,分别作出锐角三角形、直角三角形和钝角三角形的外接圆,它们外心的位置有什么特点?
五、小结反思
5.
如图是一名考古学家发现的一块古代车轮的碎片,你能帮他找出这个轮子的半径吗?说出你的理由.
A
B
C
O
五、小结反思
课后作业
试一试
请用反证法证明“两直线平行,同位角相等”.
已知:AB∥CD,
求证:∠1=∠2.
A
B
C
D
E
F
A’
B’
1
2
O
五、小结反思
思考
经过任意四个点是不是可以作一个圆?
五、小结反思
同课章节目录
