苏科版九年级数学下册第7章锐角三角函数中考演练(word解析版)
文档属性
| 名称 | 苏科版九年级数学下册第7章锐角三角函数中考演练(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 817.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 12:58:44 | ||
图片预览



文档简介
第7章 锐角三角函数
中考演练
一、选择题
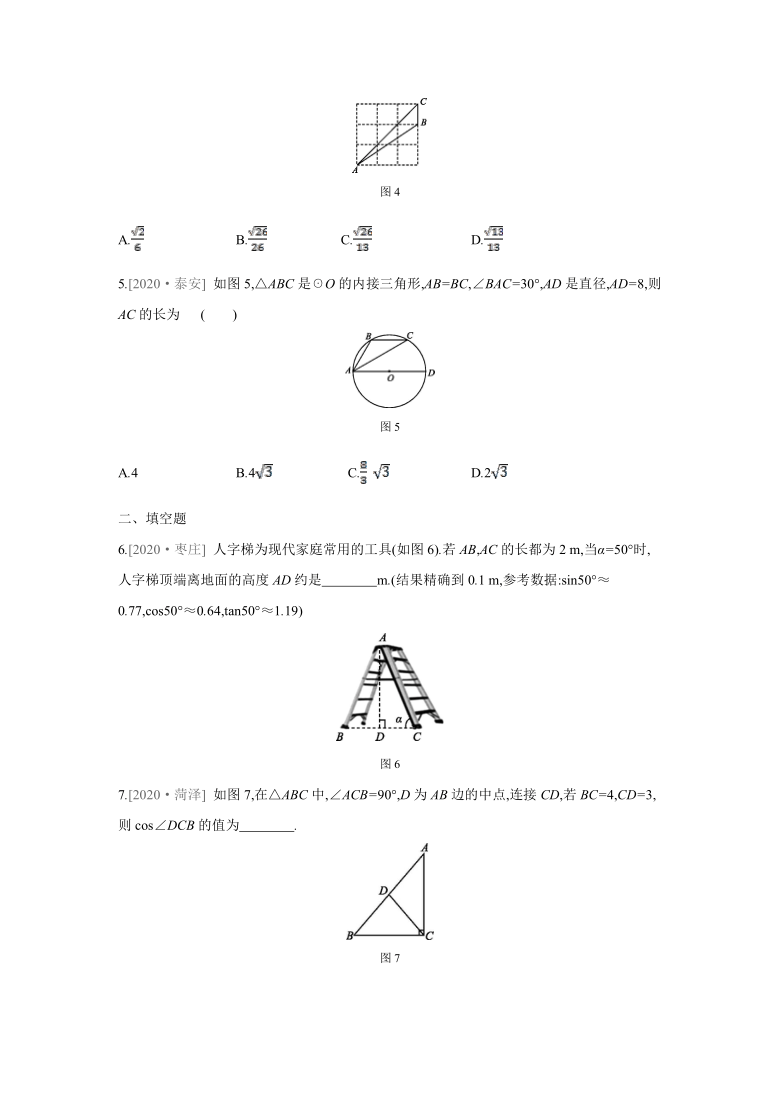
1.[2020·杭州]
如图1,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )
图1
A.c=bsinB
B.b=csinB
C.a=btanB
D.b=ctanB
2.[2020·深圳]
如图2,为了测量一条河流的宽度,一测量员在河岸边相距200米的P,Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为
( )
图2
A.200tan70°米
B.米
C.200sin70°米
D.米
3.[2020·安徽]
如图3,在Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A,若AC=4,cosA=,则BD的长度为
( )
图3
A.
B.
C.
D.4
4.[2020·南充]
如图4,点A,B,C在正方形网格的格点上,则sin∠BAC等于
( )
图4
A.
B.
C.
D.
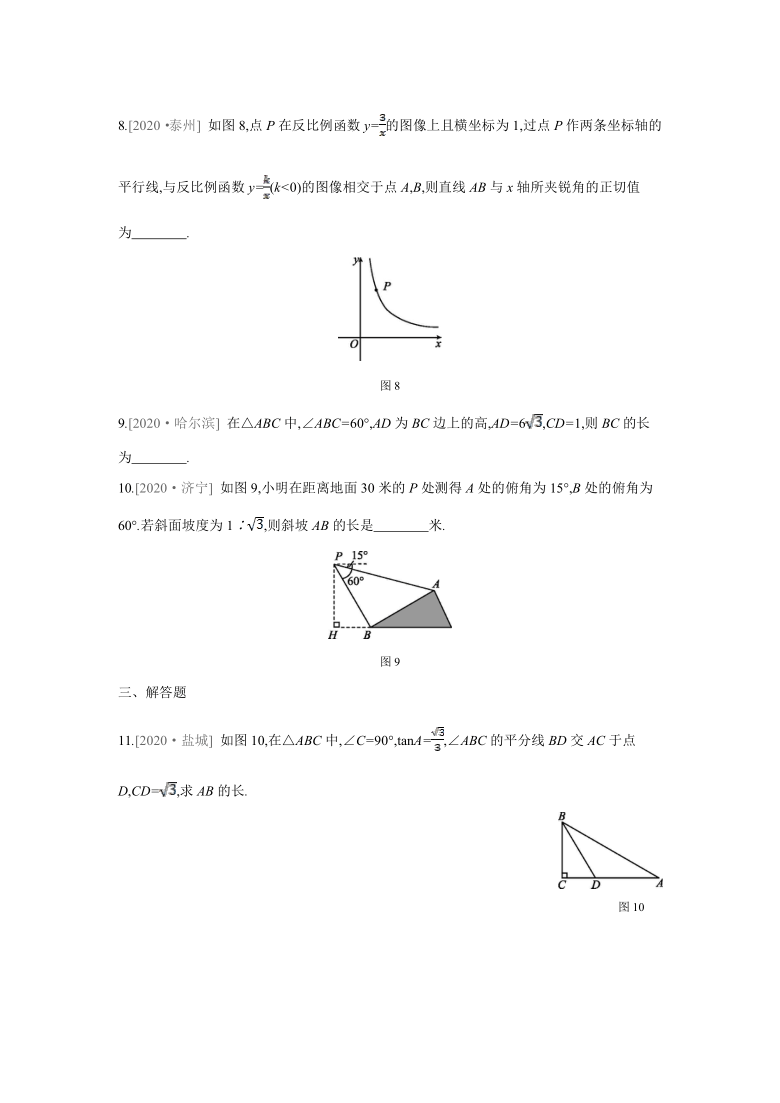
5.[2020·泰安]
如图5,△ABC是☉O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为
( )
图5
A.4
B.4
C.
D.2
二、填空题
6.[2020·枣庄]
人字梯为现代家庭常用的工具(如图6).若AB,AC的长都为2
m,当α=50°时,人字梯顶端离地面的高度AD约是 m.(结果精确到0.1
m,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)?
图6
7.[2020·菏泽]
如图7,在△ABC中,∠ACB=90°,D为AB边的中点,连接CD,若BC=4,CD=3,则cos∠DCB的值为 .?
图7
8.[2020·泰州]
如图8,点P在反比例函数y=的图像上且横坐标为1,过点P作两条坐标轴的平行线,与反比例函数y=(k<0)的图像相交于点A,B,则直线AB与x轴所夹锐角的正切值为 .?
图8
9.[2020·哈尔滨]
在△ABC中,∠ABC=60°,AD为BC边上的高,AD=6,CD=1,则BC的长为 .?
10.[2020·济宁]
如图9,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡度为1∶,则斜坡AB的长是 米.?
图9
三、解答题
11.[2020·盐城]
如图10,在△ABC中,∠C=90°,tanA=,∠ABC的平分线BD交AC于点D,CD=,求AB的长.
图10
12.[2020·内江]
为了维护我国海洋权力,海监部门对我国领海实行了常态化巡航管理.如图11,正在执行巡航任务的海监船以每小时60海里的速度向正东方向航行,在A处测得灯塔P在北偏东60°方向上,海监船继续向东航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.
(1)求B处到灯塔P的距离;
(2)已知灯塔P周围50海里范围内有暗礁,则海监船继续向正东方向航行是否安全?
图11
13.[2020·湘潭]
为了学生的安全,某校决定把一段如图12所示的步梯路段进行改造.已知四边形ABCD为矩形,DE=10
m,其坡度为i1=1∶,将步梯DE改造为斜坡AF,其坡度为i2=1∶4,求斜坡AF的长度.(结果精确到0.01
m,参考数据:≈1.732,≈4.123)
图12
14.[2019·天水]
某地的一座人行天桥如图13所示,天桥高为6米,坡面BC的坡度为1∶1,文化墙PM在天桥底部正前方8米处(PB的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1∶.
(1)求新坡面坡角α的度数;
(2)有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙PM是否需要拆除?请说明理由.
图13
答案
1.[解析]
B ∵在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,∴sinB=,即b=csinB,故A选项不成立,B选项成立;tanB=,即b=atanB,故C选项不成立,D选项不成立.故选B.
2.[解析]
B 在Rt△PQT中,∵∠QPT=90°,∠PQT=90°-70°=20°,∴∠PTQ=70°,
∴tan70°=,∴PT==,即河宽为米.故选B.
3.[解析]
C 在Rt△ABC中,cosA==,则AB=AC=5,∴BC==3.
∵∠DBC=∠A,∴cos∠DBC=cosA.
在Rt△BCD中,cos∠DBC==,
∴BD=BC=×3=.故选C.
4.[解析]
B 如图,过点B作BD⊥AC于点D.
设小正方形的边长均为1.
由勾股定理,得AB==,AC==3.∵S△ABC=AC·BD=×3·BD=×1×3,∴BD=,
∴sin∠BAC===.故选B.
5.[解析]
B 如图,连接CD.因为在△ABC中,AB=BC,∠BAC=30°,所以∠B=120°.因为四边形ABCD内接于☉O,所以∠D=60°.因为AD是☉O的直径,所以∠ACD=90°.因为sinD=,所以AC=AD·sinD=8×=4.故选B.
6.[答案]
1.5
[解析]
∵AD⊥BC,
∴∠ADC=90°,∴AD=AC·sinα=AC·sin50°≈2×0.77≈1.5(m).故答案为1.5.
7.[答案]
[解析]
如图,过点D作DE⊥BC,垂足为E.
∵∠ACB=90°,DE⊥BC,
∴DE∥AC.
又∵D为AB边的中点,
∴BE=EC=BC=2.
在Rt△DCE中,cos∠DCB==.故答案为.
8.[答案]
3
[解析]
由于点P在反比例函数y=的图像上且横坐标为1,所以P(1,3).不妨设点A在第二象限,点B在第四象限,则A,3,B(1,k),所以tan∠PAB===3.所以本题答案为3.
9.[答案]
5或7
[解析]
此题有两种情况:①点D在BC的延长线上,如图?,在△ABD中,tan∠ABD=,
∴=,解得BD=6,
∴BC=BD-CD=6-1=5;②点D在BC上,如图?,在△ABD中,tan∠ABD=,
∴=,解得BD=6,
∴BC=BD+CD=6+1=7.
综上,BC的长为5或7.
10.[答案]
20
[解析]
如图所示,过点A作AF⊥BC于点F.
∵斜面坡度为1∶,
∴tan∠ABF===,∴∠ABF=30°.
∵在P处进行观测,测得山坡上A处的俯角为15°,B处的俯角为60°,∴∠HPB=30°,∠APB=45°,∴∠HBP=60°,
∴∠PBA=90°,∠BAP=45°,∴PB=AB.
∵PH=30米,sin60°===,
解得PB=20(米),
故AB=PB=20米.
11.解:∵在Rt△ABC中,∠C=90°,tanA=,
∴∠A=30°,∠ABC=60°.
∵BD是∠ABC的平分线,∴∠CBD=∠ABD=30°.
∵CD=,∴BC==3.在Rt△ABC中,∠C=90°,∠A=30°,∴AB==6.
答:AB的长为6.
12.解:(1)∵∠PAB=30°,∠ABP=120°,
∴∠APB=180°-∠PAB-∠ABP=30°,
∴PB=AB=60海里.
(2)如图,过点P作PH⊥AB于点H.
由题意得∠PBH=60°.在Rt△PBH中,PH=PB·sin60°=60×=30(海里).
∵30>50,∴海监船继续向正东方向航行是安全的.
13.解:∵DE=10
m,其坡度为i1=1∶,
∴在Rt△DCE中,DE==2DC=10
m,∴DC=5
m.
∵四边形ABCD为矩形,∴AB=DC=5
m.
∵斜坡AF的坡度为i2=1∶4,∴=,
∴BF=4AB=20
m,∴在Rt△ABF中,AF==5≈20.62(m).
答:斜坡AF的长度约为20.62
m.
14.解:(1)∵新坡面的坡角为α,新坡面的坡度为1∶,
∴tanα==,∴α=30°.
(2)该文化墙PM不需要拆除.
理由:如图,过点C作CD⊥AB于点D,则CD=6米.
∵新坡面的坡度为1∶,
∴tan∠CAD===,
解得AD=6(米).
∵坡面BC的坡度为1∶1,CD=6米,
∴BD=6米,∴AB=AD-BD=(6-6)米.
又∵PB=8米,
∴PA=PB-AB=8-(6-6)=14-6≈14-6×1.732≈3.6(米)>3米,
∴该文化墙PM不需要拆除.
中考演练
一、选择题
1.[2020·杭州]
如图1,在△ABC中,∠C=90°,设∠A,∠B,∠C所对的边分别为a,b,c,则( )
图1
A.c=bsinB
B.b=csinB
C.a=btanB
D.b=ctanB
2.[2020·深圳]
如图2,为了测量一条河流的宽度,一测量员在河岸边相距200米的P,Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为
( )
图2
A.200tan70°米
B.米
C.200sin70°米
D.米
3.[2020·安徽]
如图3,在Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A,若AC=4,cosA=,则BD的长度为
( )
图3
A.
B.
C.
D.4
4.[2020·南充]
如图4,点A,B,C在正方形网格的格点上,则sin∠BAC等于
( )
图4
A.
B.
C.
D.
5.[2020·泰安]
如图5,△ABC是☉O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为
( )
图5
A.4
B.4
C.
D.2
二、填空题
6.[2020·枣庄]
人字梯为现代家庭常用的工具(如图6).若AB,AC的长都为2
m,当α=50°时,人字梯顶端离地面的高度AD约是 m.(结果精确到0.1
m,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)?
图6
7.[2020·菏泽]
如图7,在△ABC中,∠ACB=90°,D为AB边的中点,连接CD,若BC=4,CD=3,则cos∠DCB的值为 .?
图7
8.[2020·泰州]
如图8,点P在反比例函数y=的图像上且横坐标为1,过点P作两条坐标轴的平行线,与反比例函数y=(k<0)的图像相交于点A,B,则直线AB与x轴所夹锐角的正切值为 .?
图8
9.[2020·哈尔滨]
在△ABC中,∠ABC=60°,AD为BC边上的高,AD=6,CD=1,则BC的长为 .?
10.[2020·济宁]
如图9,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡度为1∶,则斜坡AB的长是 米.?
图9
三、解答题
11.[2020·盐城]
如图10,在△ABC中,∠C=90°,tanA=,∠ABC的平分线BD交AC于点D,CD=,求AB的长.
图10
12.[2020·内江]
为了维护我国海洋权力,海监部门对我国领海实行了常态化巡航管理.如图11,正在执行巡航任务的海监船以每小时60海里的速度向正东方向航行,在A处测得灯塔P在北偏东60°方向上,海监船继续向东航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.
(1)求B处到灯塔P的距离;
(2)已知灯塔P周围50海里范围内有暗礁,则海监船继续向正东方向航行是否安全?
图11
13.[2020·湘潭]
为了学生的安全,某校决定把一段如图12所示的步梯路段进行改造.已知四边形ABCD为矩形,DE=10
m,其坡度为i1=1∶,将步梯DE改造为斜坡AF,其坡度为i2=1∶4,求斜坡AF的长度.(结果精确到0.01
m,参考数据:≈1.732,≈4.123)
图12
14.[2019·天水]
某地的一座人行天桥如图13所示,天桥高为6米,坡面BC的坡度为1∶1,文化墙PM在天桥底部正前方8米处(PB的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1∶.
(1)求新坡面坡角α的度数;
(2)有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙PM是否需要拆除?请说明理由.
图13
答案
1.[解析]
B ∵在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,∴sinB=,即b=csinB,故A选项不成立,B选项成立;tanB=,即b=atanB,故C选项不成立,D选项不成立.故选B.
2.[解析]
B 在Rt△PQT中,∵∠QPT=90°,∠PQT=90°-70°=20°,∴∠PTQ=70°,
∴tan70°=,∴PT==,即河宽为米.故选B.
3.[解析]
C 在Rt△ABC中,cosA==,则AB=AC=5,∴BC==3.
∵∠DBC=∠A,∴cos∠DBC=cosA.
在Rt△BCD中,cos∠DBC==,
∴BD=BC=×3=.故选C.
4.[解析]
B 如图,过点B作BD⊥AC于点D.
设小正方形的边长均为1.
由勾股定理,得AB==,AC==3.∵S△ABC=AC·BD=×3·BD=×1×3,∴BD=,
∴sin∠BAC===.故选B.
5.[解析]
B 如图,连接CD.因为在△ABC中,AB=BC,∠BAC=30°,所以∠B=120°.因为四边形ABCD内接于☉O,所以∠D=60°.因为AD是☉O的直径,所以∠ACD=90°.因为sinD=,所以AC=AD·sinD=8×=4.故选B.
6.[答案]
1.5
[解析]
∵AD⊥BC,
∴∠ADC=90°,∴AD=AC·sinα=AC·sin50°≈2×0.77≈1.5(m).故答案为1.5.
7.[答案]
[解析]
如图,过点D作DE⊥BC,垂足为E.
∵∠ACB=90°,DE⊥BC,
∴DE∥AC.
又∵D为AB边的中点,
∴BE=EC=BC=2.
在Rt△DCE中,cos∠DCB==.故答案为.
8.[答案]
3
[解析]
由于点P在反比例函数y=的图像上且横坐标为1,所以P(1,3).不妨设点A在第二象限,点B在第四象限,则A,3,B(1,k),所以tan∠PAB===3.所以本题答案为3.
9.[答案]
5或7
[解析]
此题有两种情况:①点D在BC的延长线上,如图?,在△ABD中,tan∠ABD=,
∴=,解得BD=6,
∴BC=BD-CD=6-1=5;②点D在BC上,如图?,在△ABD中,tan∠ABD=,
∴=,解得BD=6,
∴BC=BD+CD=6+1=7.
综上,BC的长为5或7.
10.[答案]
20
[解析]
如图所示,过点A作AF⊥BC于点F.
∵斜面坡度为1∶,
∴tan∠ABF===,∴∠ABF=30°.
∵在P处进行观测,测得山坡上A处的俯角为15°,B处的俯角为60°,∴∠HPB=30°,∠APB=45°,∴∠HBP=60°,
∴∠PBA=90°,∠BAP=45°,∴PB=AB.
∵PH=30米,sin60°===,
解得PB=20(米),
故AB=PB=20米.
11.解:∵在Rt△ABC中,∠C=90°,tanA=,
∴∠A=30°,∠ABC=60°.
∵BD是∠ABC的平分线,∴∠CBD=∠ABD=30°.
∵CD=,∴BC==3.在Rt△ABC中,∠C=90°,∠A=30°,∴AB==6.
答:AB的长为6.
12.解:(1)∵∠PAB=30°,∠ABP=120°,
∴∠APB=180°-∠PAB-∠ABP=30°,
∴PB=AB=60海里.
(2)如图,过点P作PH⊥AB于点H.
由题意得∠PBH=60°.在Rt△PBH中,PH=PB·sin60°=60×=30(海里).
∵30>50,∴海监船继续向正东方向航行是安全的.
13.解:∵DE=10
m,其坡度为i1=1∶,
∴在Rt△DCE中,DE==2DC=10
m,∴DC=5
m.
∵四边形ABCD为矩形,∴AB=DC=5
m.
∵斜坡AF的坡度为i2=1∶4,∴=,
∴BF=4AB=20
m,∴在Rt△ABF中,AF==5≈20.62(m).
答:斜坡AF的长度约为20.62
m.
14.解:(1)∵新坡面的坡角为α,新坡面的坡度为1∶,
∴tanα==,∴α=30°.
(2)该文化墙PM不需要拆除.
理由:如图,过点C作CD⊥AB于点D,则CD=6米.
∵新坡面的坡度为1∶,
∴tan∠CAD===,
解得AD=6(米).
∵坡面BC的坡度为1∶1,CD=6米,
∴BD=6米,∴AB=AD-BD=(6-6)米.
又∵PB=8米,
∴PA=PB-AB=8-(6-6)=14-6≈14-6×1.732≈3.6(米)>3米,
∴该文化墙PM不需要拆除.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
