2020-2021学年湘教版数学八上期末模拟试题5(含答案)
文档属性
| 名称 | 2020-2021学年湘教版数学八上期末模拟试题5(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2020-2021学年湘教版数学八上期末模拟试题5
姓名:__________班级:__________考号:__________总分_________
、选择题(本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
()-1×3=( )
A. B. -6 C. - D. 6
下列式子为最简二次根式的是( )
A. B. C. D.
计算:(﹣a2)3 ( )
A.a6 B.﹣a6 C.a5 D.﹣a5
下列等式中:①=②=±4 ③=0.001 ④=﹣⑤=﹣⑥﹣(﹣)2=25中正确的有个.( )
A.2 B.3 C.4 D.5
尺规作图要求:Ⅰ、过直线外一点作这条直线的垂线;Ⅱ、作线段的垂直平分线;
Ⅲ、过直线上一点作这条直线的垂线;Ⅳ、作角的平分线.
如图是按上述要求排乱顺序的尺规作图:
则正确的配对是( )
A.①﹣Ⅳ,②﹣Ⅱ,③﹣Ⅰ,④﹣Ⅲ B.①﹣Ⅳ,②﹣Ⅲ,③﹣Ⅱ,④﹣Ⅰ
C.①﹣Ⅱ,②﹣Ⅳ,③﹣Ⅲ,④﹣Ⅰ D.①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣Ⅲ
如图,AB∥CD,AD=CD,∠1=65°,则∠2的度数是( )
A.50° B.60° C.65° D.70°
如果a<b,那么下列不等式成立的是( )
A. a﹣b>0 B. a﹣3>b﹣3 C. a>b D. ﹣3a>﹣3b
如图,在△ABC中,∠BAC=90°,AD是△ABC的高,若∠B=20°,则∠DAC=( )
A.90° B.20° C.45° D.70°
如图所示,Rt△ABC中,∠ ACB =90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E、F分别是AD、AC上的动点,使CE+EF的和最小,则这个最小值为( )
A. B. C. 3 D. 6
乐乐发现等腰三角形一腰上的高与另一腰的夹角为40°,则这个等腰三角形底角的度数为( )
A.50° B.65° C.65°或25° D.50°或40°
、填空题(本大题共8小题,每小题3分,共24分)
计算:的结果是____________.
设a﹣b=2+,b﹣c=2﹣,则a2+b2+c2﹣ab﹣ac﹣bc= .
不等式组的解集为 .
如图,△EFG≌△NMH,△EFG的周长为15cm,HN=6cm,EF=4cm,FH=1cm,则HG= ______ .
世纪公园的门票是每人5元,一次购门票满40张,每张门票可少1元.若少于40人时,一个团队至少要有________人进公园,买40张门反而合算.
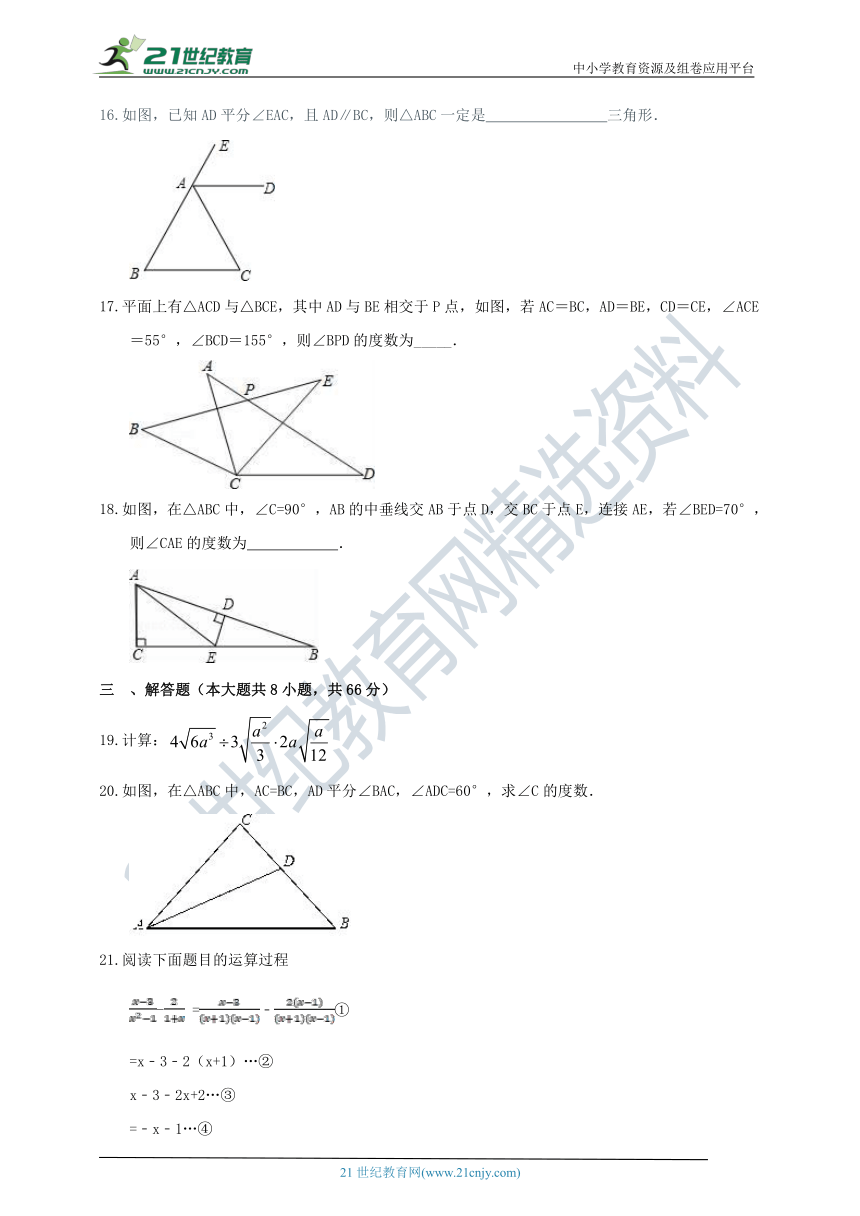
如图,已知AD平分∠EAC,且AD∥BC,则△ABC一定是???? 三角形.
平面上有△ACD与△BCE,其中AD与BE相交于P点,如图,若AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为_____.
如图,在△ABC中,∠C=90°,AB的中垂线交AB于点D,交BC于点E,连接AE,若∠BED=70°,则∠CAE的度数为 .
、解答题(本大题共8小题,共66分)
计算:
如图,在△ABC中,AC=BC,AD平分∠BAC,∠ADC=60°,求∠C的度数.
阅读下面题目的运算过程
- =﹣①
=x﹣3﹣2(x+1)…②
x﹣3﹣2x+2…③
=﹣x﹣1…④
上述计算过程,从哪一步出现错误,写出该步代号 .
(1)错误的原因 .
(2)请你写出本题正确的计算过程:
已知x=3是关于x的不等式的解,求a的取值范围.
某幼儿园计划购进一批甲、乙两种玩具,已知一件甲种玩具的价格与一件乙种玩具的价格的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的价格分别是多少元?
(2)该幼儿园计划用3500元购买甲、乙两种玩具,由于采购人员把甲、乙两种玩具的件数互换了,结果需4500元,求该幼儿园原计划购进甲、乙两种玩具各多少件?
如图,△ABC中,∠ACB=90°,CD⊥AB于点D,AO平分∠BAC,交CD于点O,E为AB上一点,且AE=AC。
(1)求证:△AOC≌△AOE;
(2)求证:OE∥BC。
江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
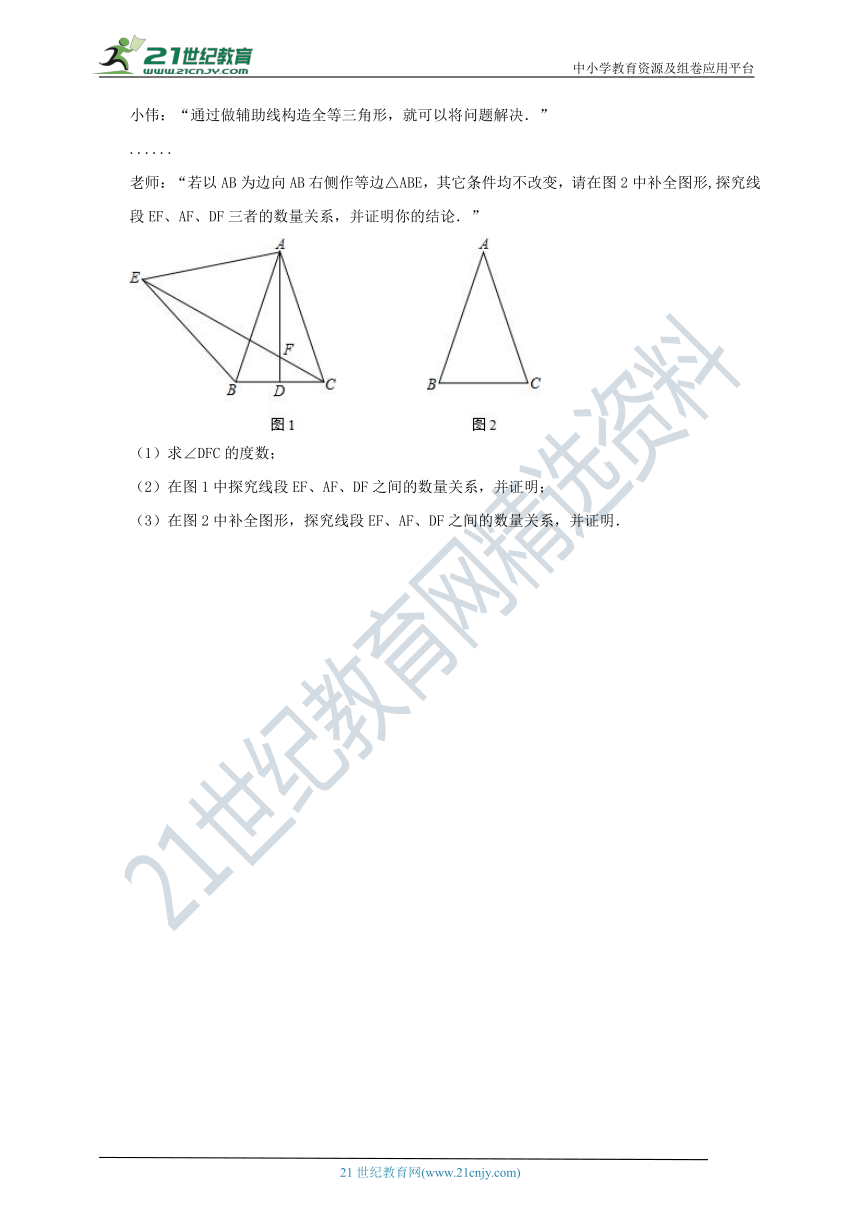
阅读下面材料,完成(1)-(3)题.
数学课上,老师出示了这样一道题:
如图1,已知等腰△ABC中,AB=AC,AD为BC边上的中线,以AB为边向AB左侧作等边△ABE,直线CE与直线AD交于点F.请探究线段EF、AF、DF之间的数量关系,并证明.
同学们经过思考后,交流了自已的想法:
小明:“通过观察和度量,发现∠DFC的度数可以求出来.”
小强:“通过观察和度量,发现线段DF和CF之间存在某种数量关系.”
小伟:“通过做辅助线构造全等三角形,就可以将问题解决.”
......
老师:“若以AB为边向AB右侧作等边△ABE,其它条件均不改变,请在图2中补全图形,探究线段EF、AF、DF三者的数量关系,并证明你的结论.”
(1)求∠DFC的度数;
(2)在图1中探究线段EF、AF、DF之间的数量关系,并证明;
(3)在图2中补全图形,探究线段EF、AF、DF之间的数量关系,并证明.
答案解析
、选择题
【考点】负整数指数幂
【分析】根据负正指数幂的定义解答
解:原式=2×3=6,
故选D.
【点评】本题考查了负整数指数幂的定义,记住a-1=.
【考点】最简二次根式
【分析】检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
解:A、被开方数不含分母;被开方数不含能开得尽方的因数或因式,故A符合题意;
B、被开方数含能开得尽方的因数或因式,故B不符合题意;
C、被开方数含能开得尽方的因数或因式,故C不符合题意;
D、被开方数含分母,故D不符合题意;
故选:A.
【点评】 此题考查了最简二次根式,熟练掌握最简二次根式的定义是解本题的关键.
【考点】幂的乘方与积的乘方.
【分析】根据积的乘方计算即可.
解:(﹣a2)3=﹣a6,
故选B.
【点评】此题考查积的乘方,关键是根据法则进行计算.
【考点】实数的运算,
【分析】原式各项计算得到结果,即可作出判断.
解:①原式=,错误;②原式=|﹣4|=4,错误;③原式=10﹣3=0.001,正确;④原式=﹣,正确;⑤原式=﹣2,正确;⑥原式=﹣5,错误,
则正确的有3个,
故选B
【点评】此题考查了实数的运算,熟练掌握运算法则是解本题的关键
【考点】基本作图-直线的垂线作法
【分析】分别利用过直线外一点作这条直线的垂线作法以及线段垂直平分线的作法和过直线上一点作这条直线的垂线、角平分线的作法分别得出符合题意的答案.
解:Ⅰ、过直线外一点作这条直线的垂线;Ⅱ、作线段的垂直平分线;
Ⅲ、过直线上一点作这条直线的垂线;Ⅳ、作角的平分线.
如图是按上述要求排乱顺序的尺规作图:
则正确的配对是:①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣Ⅲ.
故选:D.
【点评】此题主要考查了基本作图,正确掌握基本作图方法是解题关键.
【考点】平行线的性质;等腰三角形的性质
【分析】直接利用平行线的性质结合等腰三角形的性质得出∠2的度数.
解:∵AB∥CD,
∴∠1=∠ACD=65°,
∵AD=CD,
∴∠DCA=∠CAD=65°,
∴∠2的度数是:180°﹣65°﹣65°=50°.
故选:A.
【点评】此题主要考查了平行线的性质和等腰三角形的性质,正确得出∠CAD的度数是解题关键.
【考点】 不等式的性质.
【分析】 根据不等式的基本性质对每个选项进行判断.
解:a<b
A、a﹣b<0,故A选项错误;
B、a﹣3<b﹣3,故B选项错误;
C、a<b,故C选项错误;
D、﹣3a>﹣3b,故D选项正确.
故选:D.
【点评】 此题考查的知识点是不等式的性质,关键不等式的性质运用时注意:必须是加上,减去或乘以或除以同一个数或式子;另外要注意不等号的方向是否变化.
【考点】三角形的内角和定理,直角三角形的性质
【分析】先根据高线和三角形的内角和定理得:,再由余角的性质可得结论.
解:
∵AD是△ABC的高
故选:B.
【点睛】本题考查了直角三角形两锐角互余、三角形的内角和定理等知识点,熟记三角形的相关概念是解题关键.
【考点】轴对称-最短路线问题
【分析】过点C作CM⊥AB,从而得出CM的长度就是CE+EF的最小值,根据直角三角形斜边上的高线得出答案.
解:过点C作CM⊥AB,则CE+EF的最小值就是线段CM的长度,
∵AC=6,BC=8,
∴AB=10,则CM=,
故选B.
【点睛】本题主要考查的就是三角形中求最值的问题,属于中等难度题型.解决这种问题的关键就是做对称,从而得出答案.
【考点】等腰三角形的性质,三角形内角和定理
【分析】在等腰△ABC中,AB= AC,BD为腰AC上的高,∠ABD=40°,讨论:当BD在ABC内部时,如图1,先计算出∠BAD=50°,再根据等腰三角形的性质和三角形内角和可计算出∠ACB;当BD在△ABC外部时,如图2,先计算出∠BAD=50°,再根据等腰三角形的性质和三角形外角性质可计算出∠ACB.
解:在等腰△ABC中,AB= AC,BD为腰AC上的高,∠ABD=40°,
当BD在△ABC内部时,如图1,
∵BD是高,
∴∠ADB=90°,
∴∠BAD=90°-40°=50°,
∵AB=AC,
∴∠ABC=∠ACB=(180°-50°)=65°;
当BD在△ABC外部时,如图2,
∵BD是高,
∴∠ADB=90°,
∴∠BAD=90°-40°=50°,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠BAD=∠ABC+∠ACB,
∴∠ACB=∠BAD=25°,
综上,这个等腰三角形底角的度数为65°或25°.
故选:C.
【点睛】此题考查等腰三角形的性质,三角形内角和定理,解题中注意讨论思想的运用,这是解此题的关键.
、填空题
【考点】分式的混合运算
【分析】先计算括号内分式的减法、将被除式分母因式分解,再将除法转化为乘法,最后约分即可得.
解:
,
故答案为:.
【点睛】本题主要考查分式的混合运算,解题的关键是掌握分式的混合运算顺序和运算法则.
【考点】二次根式的化简求值
【分析】将a﹣b=2+和b﹣c=2﹣相加,得到a﹣c=4,再将a2+b2+c2﹣ab﹣ac﹣bc转化成关于a﹣b,b﹣c,a﹣c的完全平方的形式,再将a﹣b=2+,b﹣c=2﹣和a﹣c=4整体代入即可.
解:∵a﹣b=2+,b﹣c=2﹣,两式相加得,a﹣c=4,
原式=a2+b2+c2﹣ab﹣bc﹣ac
=
=
=
=
=
=15.
【点评】本题考查了二次根式的化简求值,解题的关键将a2+b2+c2﹣ab﹣ac﹣bc转化成关于a﹣b,b﹣c,a﹣c的完全平方的形式。
【考点】解一元一次不等式组.
【分析】分别求出求出各不等式的解集,再求出其公共解集即可.
解:,
解不等式①,得x>2.
解不等式②,得x≤3,
故不等式组的解集为2<x≤3.
故答案为2<x≤3.
【点评】本题属于基础应用题,只需学生熟练掌握求不等式组的解集的口诀,即可完成.
【考点】全等三角形的性质
【分析】首先根据全等三角形对应边相等可得MN=EF=4cm,FG=MH,△HMN的周长=△EFG的周长=15cm,再根据等式的性质可得FG-HG=MH-HG,即GM=FH,进而可得答案.
解:∵△EFG≌△NMH,
∴MN=EF=4cm,FG=MH,△HMN的周长=△EFG的周长=15cm,
∴FG-HG=MH-HG,即FH=GM=1cm,
∵△EFG的周长为15cm,
∴HM=15-6-4=5cm,
∴HG=5-1=4cm .
故答案为:4cm.
【点睛】本题考查全等三角形的性质,解题关键是掌握全等三角形对应边相等.
【考点】一元一次不等式的应用
【分析】先求出购买40张票,优惠后需要多少钱,然后再利用5x>160时,求出买到的张数的取值范围再加上1即可.
解:设x人进公园,
若购满40张票则需要:40×(5-1)=40×4=160(元),
故5x>160时,
解得:x>32,
∴当有32人时,购买32张票和40张票的价格相同,
则再多1人时买40张票较合算;
∴32+1=33(人);
则至少要有33人去世纪公园,买40张票反而合算.
故答案为:33.
【点评】此题主要考查了一元一次不等式的应用,找到按5元的单价付款和4元单价付款的等量关系是解决本题的关键.
【考点】平行线的性质,等腰三角形的判定,角平分线的性质
【分析】先根据平行线性质得到∠EAD=∠B,∠DAC=∠C,再根据角平分线的性质得到∠EAD=∠DAC,从而推出∠B=∠C,等角对等边所以AB=AC.从而判定△ABC的形状.
解:∵AD∥BC,
∴∠EAD=∠B,∠DAC=∠C.
∵AD平分∠EAC,
∴∠EAD=∠DAC.
∴∠B=∠C.
∴AB=AC.
∴△ABC是等腰三角形.
故答案为:等腰.
【点评】此题主要考查了等腰三角形的判定及平行线的性质,重点考查学生对等腰三角形的判定的理解及运用,属于基础证明,难度不算很大.
【考点】三角形的内角和定理,全等三角形的判定与性质
【分析】易证△ACD≌△BCE,由全等三角形的性质可知:∠A=∠B,再根据已知条件和四边形的内角和为360°,即可求出∠BPD的度数.
解:在△ACD和△BCE中,
,
∴△ACD≌△BCE(SSS),
∴∠A=∠B,∠BCE=∠ACD,
∴∠BCA=∠ECD,
∵∠ACE=55°,∠BCD=155°,
∴∠BCA+∠ECD=100°,
∴∠BCA=∠ECD=50°,
∵∠ACE=55°,
∴∠ACD=105°
∴∠A+∠D=75°,
∴∠B+∠D=75°,
∵∠BCD=155°,
∴∠BPD=360°﹣75°﹣155°=130°,
故答案为:130°.
【点睛】本题考查了全等三角形的判定和性质、三角形的内角和定理以及四边形的内角和定理,解题的关键是利用整体的数学思想求出∠B+∠D=75°.
【考点】线段垂直平分线的性质.
【分析】根据直角三角形的性质求出∠B和∠BAC的度数,根据线段的垂直平分线的性质求出∠EAD的度数,计算得到答案.
解:在直角△BDE中,∠BED=70°,则∠B=20°,
∴∠BAC=70°,
∵ED是AB的中垂线,
∴EA=EB,
∴∠EAD=∠B=20°,
∴∠CAE=∠BAC﹣∠EAD=50°,
故答案为:50°.
【点评】本题主要考查线段的垂直平分线的性质等几何知识,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
、解答题
【考点】二次根式的混合运算
【分析】先化简,再根据二次根式乘除法法则计算即可得答案.
解:
=4a÷a·
=4·
=
【点睛】本题考查二次根式的乘除法,熟练掌握运算法则是解题关键.
【考点】等腰三角形的性质,角平分线定义,三角形内角和定理,三角形外角的性质
【分析】设∠BAD=x.由AD平分∠BAC,得出∠CAD=∠BAD=x,∠BAC=2∠BAD=2x.由AC=BC,得出∠B=∠BAC=2x.根据三角形外角的性质得出∠ADC=∠B+∠BAD=60°,即2x+x=60°,求得x=20°,那么∠B=∠BAC=40°.然后在△ABC中,根据三角形内角和定理得出∠C=180°﹣∠B﹣∠BAC=100°.
解:设∠BAD=x.
∵AD平分∠BAC,
∴∠CAD=∠BAD=x,∠BAC=2∠BAD=2x.
∵AC=BC,
∴∠B=∠BAC=2x.
∵∠ADC=∠B+∠BAD=60°,
∴2x+x=60°,
∴x=20°,
∴∠B=∠BAC=40°.
在△ABC中,∵∠BAC+∠B+∠C=180°,
∴∠C=180°﹣∠B﹣∠BAC=100°.
【点评】本题考查了等腰三角形的性质,角平分线定义,三角形内角和定理,三角形外角的性质,难度适中.设∠BAD=x,利用∠ADC=60°列出关于x的方程是解题的关键.
【考点】分式的加减
【分析】观察解题过程,可发现②中小括号中不应该变号,错误.
解:错误步代号②.
(1)错误的原因__同分母分式加减法法则是分母不变,不是去分母;
(2)正确的计算过程:﹣=﹣=
=
=﹣.
故答案为:②;(1)同分母分式加减法法则是分母不变,不是去分母.
【点睛】本题考查了分式的化简,掌握符号的变化和正确通分是解决本题的关键.
【考点】不等式的解集.
【分析】先根据不等式,解此不等式,再对a分类讨论,即可求出a的取值范围.
解:
解得(14﹣3a)x>6
当a<,x>,又x=3是关于x的不等式的解,则<3,解得a<4;
当a>,x<,又x=3是关于x的不等式的解,则>3,解得a<4(与所设条件不符,舍去);
综上得a<4.
故a的取值范围是a<4.
【点评】本题考查了不等式的解的定义及一元一次不等式的解法,比较简单,注意分类讨论是解题的关键.
【考点】二元一次方程组的应用,分式方程的应用
【分析】(1)设甲种玩具进价x元/件,则乙种玩具进价为(40-x)元/件,根据已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同可列方程求解.
(2)设购进甲种玩具a件,则购进乙种玩具b件,根据把甲、乙两种玩具的件数互换了,结果需4500元,可列出方程组求解.
解:设甲种玩具进价x元/件,则乙种玩具进价为(40﹣x)元/件,
,
解得:x=15,
经检验x=15是原方程的解.
∴40﹣x=25.
甲,乙两种玩具分别是15元/件,25元/件;
(2)设购进甲种玩具a件,则购进乙种玩具b件,,
解得:,
答:原计划购进甲、乙两种玩具各150件,50件.
【点睛】本题考查分式方程的应用,二元一次方程组的应用,第一问以件数做为等量关系列方程求解,不要忘记检验;第2问以玩具件数和钱数做为等量关系列方程组求解.
【考点】全等三角形的判定与性质
【分析】(1)由AO平分∠BAC,可得∠CAO=∠EAO结合AO=AO,AE=AC即可由“SAS”证得:△AOC≌△AOE;
(2)由△AOC≌△AOE可得∠ACO=∠AEO,由∠ACB=90°,CD⊥AB于点D,易得∠ACO+∠DCB=90°,∠AEO+∠EOD=90°,从而可得∠DCB=∠DOE,即可得到:OE∥BC.
解:(1)∵AO平分∠BAC,
∴∠CAO=∠EAO.
在△ACO和△AEO中:
,
∴△AOC≌△AOE.
(2)∵△AOC≌△AOE,
∴∠ACO=∠AEO,
∵ CD⊥AB于点D,
∴∠ODE=∠ACB=90°,
∴∠ACO+∠DCB=90°,∠AEO+∠EOD=90°,
∴∠DCB=∠DOE,
∴OE∥BC.
【点睛】此题考查三角形全等的判定和平行线的判定,解题关键在于熟练掌握三角形全等的判定法则
【考点】一元一次不等式组的应用; 二元一次方程组的应用.
【分析】(1)设每台大型收割机1小时收割小麦x公顷,每台小型收割机1小时收割小麦y公顷,根据“1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设大型收割机有m台,总费用为w元,则小型收割机有(10﹣m)台,根据总费用=大型收割机的费用+小型收割机的费用,即可得出w与m之间的函数关系式,由“要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元”,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,依此可找出各方案,再结合一次函数的性质即可解决最值问题.
解:(1)设每台大型收割机1小时收割小麦x公顷,每台小型收割机1小时收割小麦y公顷,
根据题意得:,
解得:.
答:每台大型收割机1小时收割小麦0.5公顷,每台小型收割机1小时收割小麦0.3公顷.
(2)设大型收割机有m台,总费用为w元,则小型收割机有(10﹣m)台,
根据题意得:w=300×2m+200×2(10﹣m)=200m+4000.
∵2小时完成8公顷小麦的收割任务,且总费用不超过5400元,
∴,
解得:5≤m≤7,
∴有三种不同方案.
∵w=200m+4000中,200>0,
∴w值随m值的增大而增大,
∴当m=5时,总费用取最小值,最小值为5000元.
答:有三种方案,当大型收割机和小型收割机各5台时,总费用最低,最低费用为5000元.
【考点】全等三角形的判定和性质,等边三角形的性质,等腰三角形的性质
【分析】(1)可设∠BAD=∠CAD=α,∠AEC=∠ACE=β,在△ACE中,根据三角形内角和可得2α+60+2β=180°,从而有α+β=60°,即可得出∠DFC的度数;
(2)在EC上截取EG=CF,连接AG,证明△AEG≌△ACF,然后再证明△AFG为等边三角形,从而可得出EF=EG+GF=AF+FC;
(3)在AF上截取AG=EF,连接BG,BF,证明方法类似(2),先证明△ABG≌△EBF,再证明△BFG为等边三角形,最后可得出结论.
解:(1)∵AB=AC,AD为BC边上的中线,∴可设∠BAD=∠CAD=α,
又△ABE为等边三角形,
∴AE=AB=AC,∠EAB=60°,∴可设∠AEC=∠ACE=β,
在△ACE中,2α+60°+2β=180°,
∴α+β=60°,
∴∠DFC=α+β=60°;
(2)EF=AF+FC,证明如下:
∵AB=AC,AD为BC边上的中线,∴AD⊥BC,∴∠FDC=90°,
∵∠CFD=60°,则∠DCF=30°,
∴CF=2DF,
在EC上截取EG=CF,连接AG,
又AE=AC,
∴∠AEG=∠ACF,
∴△AEG≌△ACF(SAS),
∴∠EAG=∠CAF,AG=AF,
又∠CAF=∠BAD,
∴∠EAG=∠BAD,
∴∠GAF=∠BAD+∠BAG=∠EAG+∠BAG=∠60°,
∴△AFG为等边三角形,
∴EF=EG+GF=AF+FC,
即EF=AF+FC;
(3)补全图形如图所示,
结论:AF=EF+2DF.证明如下:
同(1)可设∠BAD=∠CAD=α,∠ACE=∠AEC=β,
∴∠CAE=180°-2β,
∴∠BAE=2α+180°-2β=60°,∴β-α=60°,
∴∠AFC=β-α=60°,
又△ABE为等边三角形,∴∠ABE=∠AFC=60°,
∴由8字图可得:∠BAD=∠BEF,
在AF上截取AG=EF,连接BG,BF,
又AB=BE,
∴△ABG≌△EBF(SAS),
∴BG=BF,
又AF垂直平分BC,
∴BF=CF,
∴∠BFA=∠AFC=60°,
∴△BFG为等边三角形,
∴BG=BF,又BC⊥FG,∴FG=BF=2DF,
∴AF=AG+GF=BF+EF=2DF+EF.
【点睛】本题考查了全等三角形的判定和性质、等边三角形的性质、等腰三角形的性质等知识,解决问题的关键是常用辅助线构造全等三角形,属于中考常考题型.
_21?????????è?????(www.21cnjy.com)_
2020-2021学年湘教版数学八上期末模拟试题5
姓名:__________班级:__________考号:__________总分_________
、选择题(本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一个选项是符合题目要求的)
()-1×3=( )
A. B. -6 C. - D. 6
下列式子为最简二次根式的是( )
A. B. C. D.
计算:(﹣a2)3 ( )
A.a6 B.﹣a6 C.a5 D.﹣a5
下列等式中:①=②=±4 ③=0.001 ④=﹣⑤=﹣⑥﹣(﹣)2=25中正确的有个.( )
A.2 B.3 C.4 D.5
尺规作图要求:Ⅰ、过直线外一点作这条直线的垂线;Ⅱ、作线段的垂直平分线;
Ⅲ、过直线上一点作这条直线的垂线;Ⅳ、作角的平分线.
如图是按上述要求排乱顺序的尺规作图:
则正确的配对是( )
A.①﹣Ⅳ,②﹣Ⅱ,③﹣Ⅰ,④﹣Ⅲ B.①﹣Ⅳ,②﹣Ⅲ,③﹣Ⅱ,④﹣Ⅰ
C.①﹣Ⅱ,②﹣Ⅳ,③﹣Ⅲ,④﹣Ⅰ D.①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣Ⅲ
如图,AB∥CD,AD=CD,∠1=65°,则∠2的度数是( )
A.50° B.60° C.65° D.70°
如果a<b,那么下列不等式成立的是( )
A. a﹣b>0 B. a﹣3>b﹣3 C. a>b D. ﹣3a>﹣3b
如图,在△ABC中,∠BAC=90°,AD是△ABC的高,若∠B=20°,则∠DAC=( )
A.90° B.20° C.45° D.70°
如图所示,Rt△ABC中,∠ ACB =90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E、F分别是AD、AC上的动点,使CE+EF的和最小,则这个最小值为( )
A. B. C. 3 D. 6
乐乐发现等腰三角形一腰上的高与另一腰的夹角为40°,则这个等腰三角形底角的度数为( )
A.50° B.65° C.65°或25° D.50°或40°
、填空题(本大题共8小题,每小题3分,共24分)
计算:的结果是____________.
设a﹣b=2+,b﹣c=2﹣,则a2+b2+c2﹣ab﹣ac﹣bc= .
不等式组的解集为 .
如图,△EFG≌△NMH,△EFG的周长为15cm,HN=6cm,EF=4cm,FH=1cm,则HG= ______ .
世纪公园的门票是每人5元,一次购门票满40张,每张门票可少1元.若少于40人时,一个团队至少要有________人进公园,买40张门反而合算.
如图,已知AD平分∠EAC,且AD∥BC,则△ABC一定是???? 三角形.
平面上有△ACD与△BCE,其中AD与BE相交于P点,如图,若AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为_____.
如图,在△ABC中,∠C=90°,AB的中垂线交AB于点D,交BC于点E,连接AE,若∠BED=70°,则∠CAE的度数为 .
、解答题(本大题共8小题,共66分)
计算:
如图,在△ABC中,AC=BC,AD平分∠BAC,∠ADC=60°,求∠C的度数.
阅读下面题目的运算过程
- =﹣①
=x﹣3﹣2(x+1)…②
x﹣3﹣2x+2…③
=﹣x﹣1…④
上述计算过程,从哪一步出现错误,写出该步代号 .
(1)错误的原因 .
(2)请你写出本题正确的计算过程:
已知x=3是关于x的不等式的解,求a的取值范围.
某幼儿园计划购进一批甲、乙两种玩具,已知一件甲种玩具的价格与一件乙种玩具的价格的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的价格分别是多少元?
(2)该幼儿园计划用3500元购买甲、乙两种玩具,由于采购人员把甲、乙两种玩具的件数互换了,结果需4500元,求该幼儿园原计划购进甲、乙两种玩具各多少件?
如图,△ABC中,∠ACB=90°,CD⊥AB于点D,AO平分∠BAC,交CD于点O,E为AB上一点,且AE=AC。
(1)求证:△AOC≌△AOE;
(2)求证:OE∥BC。
江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
阅读下面材料,完成(1)-(3)题.
数学课上,老师出示了这样一道题:
如图1,已知等腰△ABC中,AB=AC,AD为BC边上的中线,以AB为边向AB左侧作等边△ABE,直线CE与直线AD交于点F.请探究线段EF、AF、DF之间的数量关系,并证明.
同学们经过思考后,交流了自已的想法:
小明:“通过观察和度量,发现∠DFC的度数可以求出来.”
小强:“通过观察和度量,发现线段DF和CF之间存在某种数量关系.”
小伟:“通过做辅助线构造全等三角形,就可以将问题解决.”
......
老师:“若以AB为边向AB右侧作等边△ABE,其它条件均不改变,请在图2中补全图形,探究线段EF、AF、DF三者的数量关系,并证明你的结论.”
(1)求∠DFC的度数;
(2)在图1中探究线段EF、AF、DF之间的数量关系,并证明;
(3)在图2中补全图形,探究线段EF、AF、DF之间的数量关系,并证明.
答案解析
、选择题
【考点】负整数指数幂
【分析】根据负正指数幂的定义解答
解:原式=2×3=6,
故选D.
【点评】本题考查了负整数指数幂的定义,记住a-1=.
【考点】最简二次根式
【分析】检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
解:A、被开方数不含分母;被开方数不含能开得尽方的因数或因式,故A符合题意;
B、被开方数含能开得尽方的因数或因式,故B不符合题意;
C、被开方数含能开得尽方的因数或因式,故C不符合题意;
D、被开方数含分母,故D不符合题意;
故选:A.
【点评】 此题考查了最简二次根式,熟练掌握最简二次根式的定义是解本题的关键.
【考点】幂的乘方与积的乘方.
【分析】根据积的乘方计算即可.
解:(﹣a2)3=﹣a6,
故选B.
【点评】此题考查积的乘方,关键是根据法则进行计算.
【考点】实数的运算,
【分析】原式各项计算得到结果,即可作出判断.
解:①原式=,错误;②原式=|﹣4|=4,错误;③原式=10﹣3=0.001,正确;④原式=﹣,正确;⑤原式=﹣2,正确;⑥原式=﹣5,错误,
则正确的有3个,
故选B
【点评】此题考查了实数的运算,熟练掌握运算法则是解本题的关键
【考点】基本作图-直线的垂线作法
【分析】分别利用过直线外一点作这条直线的垂线作法以及线段垂直平分线的作法和过直线上一点作这条直线的垂线、角平分线的作法分别得出符合题意的答案.
解:Ⅰ、过直线外一点作这条直线的垂线;Ⅱ、作线段的垂直平分线;
Ⅲ、过直线上一点作这条直线的垂线;Ⅳ、作角的平分线.
如图是按上述要求排乱顺序的尺规作图:
则正确的配对是:①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣Ⅲ.
故选:D.
【点评】此题主要考查了基本作图,正确掌握基本作图方法是解题关键.
【考点】平行线的性质;等腰三角形的性质
【分析】直接利用平行线的性质结合等腰三角形的性质得出∠2的度数.
解:∵AB∥CD,
∴∠1=∠ACD=65°,
∵AD=CD,
∴∠DCA=∠CAD=65°,
∴∠2的度数是:180°﹣65°﹣65°=50°.
故选:A.
【点评】此题主要考查了平行线的性质和等腰三角形的性质,正确得出∠CAD的度数是解题关键.
【考点】 不等式的性质.
【分析】 根据不等式的基本性质对每个选项进行判断.
解:a<b
A、a﹣b<0,故A选项错误;
B、a﹣3<b﹣3,故B选项错误;
C、a<b,故C选项错误;
D、﹣3a>﹣3b,故D选项正确.
故选:D.
【点评】 此题考查的知识点是不等式的性质,关键不等式的性质运用时注意:必须是加上,减去或乘以或除以同一个数或式子;另外要注意不等号的方向是否变化.
【考点】三角形的内角和定理,直角三角形的性质
【分析】先根据高线和三角形的内角和定理得:,再由余角的性质可得结论.
解:
∵AD是△ABC的高
故选:B.
【点睛】本题考查了直角三角形两锐角互余、三角形的内角和定理等知识点,熟记三角形的相关概念是解题关键.
【考点】轴对称-最短路线问题
【分析】过点C作CM⊥AB,从而得出CM的长度就是CE+EF的最小值,根据直角三角形斜边上的高线得出答案.
解:过点C作CM⊥AB,则CE+EF的最小值就是线段CM的长度,
∵AC=6,BC=8,
∴AB=10,则CM=,
故选B.
【点睛】本题主要考查的就是三角形中求最值的问题,属于中等难度题型.解决这种问题的关键就是做对称,从而得出答案.
【考点】等腰三角形的性质,三角形内角和定理
【分析】在等腰△ABC中,AB= AC,BD为腰AC上的高,∠ABD=40°,讨论:当BD在ABC内部时,如图1,先计算出∠BAD=50°,再根据等腰三角形的性质和三角形内角和可计算出∠ACB;当BD在△ABC外部时,如图2,先计算出∠BAD=50°,再根据等腰三角形的性质和三角形外角性质可计算出∠ACB.
解:在等腰△ABC中,AB= AC,BD为腰AC上的高,∠ABD=40°,
当BD在△ABC内部时,如图1,
∵BD是高,
∴∠ADB=90°,
∴∠BAD=90°-40°=50°,
∵AB=AC,
∴∠ABC=∠ACB=(180°-50°)=65°;
当BD在△ABC外部时,如图2,
∵BD是高,
∴∠ADB=90°,
∴∠BAD=90°-40°=50°,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠BAD=∠ABC+∠ACB,
∴∠ACB=∠BAD=25°,
综上,这个等腰三角形底角的度数为65°或25°.
故选:C.
【点睛】此题考查等腰三角形的性质,三角形内角和定理,解题中注意讨论思想的运用,这是解此题的关键.
、填空题
【考点】分式的混合运算
【分析】先计算括号内分式的减法、将被除式分母因式分解,再将除法转化为乘法,最后约分即可得.
解:
,
故答案为:.
【点睛】本题主要考查分式的混合运算,解题的关键是掌握分式的混合运算顺序和运算法则.
【考点】二次根式的化简求值
【分析】将a﹣b=2+和b﹣c=2﹣相加,得到a﹣c=4,再将a2+b2+c2﹣ab﹣ac﹣bc转化成关于a﹣b,b﹣c,a﹣c的完全平方的形式,再将a﹣b=2+,b﹣c=2﹣和a﹣c=4整体代入即可.
解:∵a﹣b=2+,b﹣c=2﹣,两式相加得,a﹣c=4,
原式=a2+b2+c2﹣ab﹣bc﹣ac
=
=
=
=
=
=15.
【点评】本题考查了二次根式的化简求值,解题的关键将a2+b2+c2﹣ab﹣ac﹣bc转化成关于a﹣b,b﹣c,a﹣c的完全平方的形式。
【考点】解一元一次不等式组.
【分析】分别求出求出各不等式的解集,再求出其公共解集即可.
解:,
解不等式①,得x>2.
解不等式②,得x≤3,
故不等式组的解集为2<x≤3.
故答案为2<x≤3.
【点评】本题属于基础应用题,只需学生熟练掌握求不等式组的解集的口诀,即可完成.
【考点】全等三角形的性质
【分析】首先根据全等三角形对应边相等可得MN=EF=4cm,FG=MH,△HMN的周长=△EFG的周长=15cm,再根据等式的性质可得FG-HG=MH-HG,即GM=FH,进而可得答案.
解:∵△EFG≌△NMH,
∴MN=EF=4cm,FG=MH,△HMN的周长=△EFG的周长=15cm,
∴FG-HG=MH-HG,即FH=GM=1cm,
∵△EFG的周长为15cm,
∴HM=15-6-4=5cm,
∴HG=5-1=4cm .
故答案为:4cm.
【点睛】本题考查全等三角形的性质,解题关键是掌握全等三角形对应边相等.
【考点】一元一次不等式的应用
【分析】先求出购买40张票,优惠后需要多少钱,然后再利用5x>160时,求出买到的张数的取值范围再加上1即可.
解:设x人进公园,
若购满40张票则需要:40×(5-1)=40×4=160(元),
故5x>160时,
解得:x>32,
∴当有32人时,购买32张票和40张票的价格相同,
则再多1人时买40张票较合算;
∴32+1=33(人);
则至少要有33人去世纪公园,买40张票反而合算.
故答案为:33.
【点评】此题主要考查了一元一次不等式的应用,找到按5元的单价付款和4元单价付款的等量关系是解决本题的关键.
【考点】平行线的性质,等腰三角形的判定,角平分线的性质
【分析】先根据平行线性质得到∠EAD=∠B,∠DAC=∠C,再根据角平分线的性质得到∠EAD=∠DAC,从而推出∠B=∠C,等角对等边所以AB=AC.从而判定△ABC的形状.
解:∵AD∥BC,
∴∠EAD=∠B,∠DAC=∠C.
∵AD平分∠EAC,
∴∠EAD=∠DAC.
∴∠B=∠C.
∴AB=AC.
∴△ABC是等腰三角形.
故答案为:等腰.
【点评】此题主要考查了等腰三角形的判定及平行线的性质,重点考查学生对等腰三角形的判定的理解及运用,属于基础证明,难度不算很大.
【考点】三角形的内角和定理,全等三角形的判定与性质
【分析】易证△ACD≌△BCE,由全等三角形的性质可知:∠A=∠B,再根据已知条件和四边形的内角和为360°,即可求出∠BPD的度数.
解:在△ACD和△BCE中,
,
∴△ACD≌△BCE(SSS),
∴∠A=∠B,∠BCE=∠ACD,
∴∠BCA=∠ECD,
∵∠ACE=55°,∠BCD=155°,
∴∠BCA+∠ECD=100°,
∴∠BCA=∠ECD=50°,
∵∠ACE=55°,
∴∠ACD=105°
∴∠A+∠D=75°,
∴∠B+∠D=75°,
∵∠BCD=155°,
∴∠BPD=360°﹣75°﹣155°=130°,
故答案为:130°.
【点睛】本题考查了全等三角形的判定和性质、三角形的内角和定理以及四边形的内角和定理,解题的关键是利用整体的数学思想求出∠B+∠D=75°.
【考点】线段垂直平分线的性质.
【分析】根据直角三角形的性质求出∠B和∠BAC的度数,根据线段的垂直平分线的性质求出∠EAD的度数,计算得到答案.
解:在直角△BDE中,∠BED=70°,则∠B=20°,
∴∠BAC=70°,
∵ED是AB的中垂线,
∴EA=EB,
∴∠EAD=∠B=20°,
∴∠CAE=∠BAC﹣∠EAD=50°,
故答案为:50°.
【点评】本题主要考查线段的垂直平分线的性质等几何知识,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
、解答题
【考点】二次根式的混合运算
【分析】先化简,再根据二次根式乘除法法则计算即可得答案.
解:
=4a÷a·
=4·
=
【点睛】本题考查二次根式的乘除法,熟练掌握运算法则是解题关键.
【考点】等腰三角形的性质,角平分线定义,三角形内角和定理,三角形外角的性质
【分析】设∠BAD=x.由AD平分∠BAC,得出∠CAD=∠BAD=x,∠BAC=2∠BAD=2x.由AC=BC,得出∠B=∠BAC=2x.根据三角形外角的性质得出∠ADC=∠B+∠BAD=60°,即2x+x=60°,求得x=20°,那么∠B=∠BAC=40°.然后在△ABC中,根据三角形内角和定理得出∠C=180°﹣∠B﹣∠BAC=100°.
解:设∠BAD=x.
∵AD平分∠BAC,
∴∠CAD=∠BAD=x,∠BAC=2∠BAD=2x.
∵AC=BC,
∴∠B=∠BAC=2x.
∵∠ADC=∠B+∠BAD=60°,
∴2x+x=60°,
∴x=20°,
∴∠B=∠BAC=40°.
在△ABC中,∵∠BAC+∠B+∠C=180°,
∴∠C=180°﹣∠B﹣∠BAC=100°.
【点评】本题考查了等腰三角形的性质,角平分线定义,三角形内角和定理,三角形外角的性质,难度适中.设∠BAD=x,利用∠ADC=60°列出关于x的方程是解题的关键.
【考点】分式的加减
【分析】观察解题过程,可发现②中小括号中不应该变号,错误.
解:错误步代号②.
(1)错误的原因__同分母分式加减法法则是分母不变,不是去分母;
(2)正确的计算过程:﹣=﹣=
=
=﹣.
故答案为:②;(1)同分母分式加减法法则是分母不变,不是去分母.
【点睛】本题考查了分式的化简,掌握符号的变化和正确通分是解决本题的关键.
【考点】不等式的解集.
【分析】先根据不等式,解此不等式,再对a分类讨论,即可求出a的取值范围.
解:
解得(14﹣3a)x>6
当a<,x>,又x=3是关于x的不等式的解,则<3,解得a<4;
当a>,x<,又x=3是关于x的不等式的解,则>3,解得a<4(与所设条件不符,舍去);
综上得a<4.
故a的取值范围是a<4.
【点评】本题考查了不等式的解的定义及一元一次不等式的解法,比较简单,注意分类讨论是解题的关键.
【考点】二元一次方程组的应用,分式方程的应用
【分析】(1)设甲种玩具进价x元/件,则乙种玩具进价为(40-x)元/件,根据已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同可列方程求解.
(2)设购进甲种玩具a件,则购进乙种玩具b件,根据把甲、乙两种玩具的件数互换了,结果需4500元,可列出方程组求解.
解:设甲种玩具进价x元/件,则乙种玩具进价为(40﹣x)元/件,
,
解得:x=15,
经检验x=15是原方程的解.
∴40﹣x=25.
甲,乙两种玩具分别是15元/件,25元/件;
(2)设购进甲种玩具a件,则购进乙种玩具b件,,
解得:,
答:原计划购进甲、乙两种玩具各150件,50件.
【点睛】本题考查分式方程的应用,二元一次方程组的应用,第一问以件数做为等量关系列方程求解,不要忘记检验;第2问以玩具件数和钱数做为等量关系列方程组求解.
【考点】全等三角形的判定与性质
【分析】(1)由AO平分∠BAC,可得∠CAO=∠EAO结合AO=AO,AE=AC即可由“SAS”证得:△AOC≌△AOE;
(2)由△AOC≌△AOE可得∠ACO=∠AEO,由∠ACB=90°,CD⊥AB于点D,易得∠ACO+∠DCB=90°,∠AEO+∠EOD=90°,从而可得∠DCB=∠DOE,即可得到:OE∥BC.
解:(1)∵AO平分∠BAC,
∴∠CAO=∠EAO.
在△ACO和△AEO中:
,
∴△AOC≌△AOE.
(2)∵△AOC≌△AOE,
∴∠ACO=∠AEO,
∵ CD⊥AB于点D,
∴∠ODE=∠ACB=90°,
∴∠ACO+∠DCB=90°,∠AEO+∠EOD=90°,
∴∠DCB=∠DOE,
∴OE∥BC.
【点睛】此题考查三角形全等的判定和平行线的判定,解题关键在于熟练掌握三角形全等的判定法则
【考点】一元一次不等式组的应用; 二元一次方程组的应用.
【分析】(1)设每台大型收割机1小时收割小麦x公顷,每台小型收割机1小时收割小麦y公顷,根据“1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设大型收割机有m台,总费用为w元,则小型收割机有(10﹣m)台,根据总费用=大型收割机的费用+小型收割机的费用,即可得出w与m之间的函数关系式,由“要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元”,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,依此可找出各方案,再结合一次函数的性质即可解决最值问题.
解:(1)设每台大型收割机1小时收割小麦x公顷,每台小型收割机1小时收割小麦y公顷,
根据题意得:,
解得:.
答:每台大型收割机1小时收割小麦0.5公顷,每台小型收割机1小时收割小麦0.3公顷.
(2)设大型收割机有m台,总费用为w元,则小型收割机有(10﹣m)台,
根据题意得:w=300×2m+200×2(10﹣m)=200m+4000.
∵2小时完成8公顷小麦的收割任务,且总费用不超过5400元,
∴,
解得:5≤m≤7,
∴有三种不同方案.
∵w=200m+4000中,200>0,
∴w值随m值的增大而增大,
∴当m=5时,总费用取最小值,最小值为5000元.
答:有三种方案,当大型收割机和小型收割机各5台时,总费用最低,最低费用为5000元.
【考点】全等三角形的判定和性质,等边三角形的性质,等腰三角形的性质
【分析】(1)可设∠BAD=∠CAD=α,∠AEC=∠ACE=β,在△ACE中,根据三角形内角和可得2α+60+2β=180°,从而有α+β=60°,即可得出∠DFC的度数;
(2)在EC上截取EG=CF,连接AG,证明△AEG≌△ACF,然后再证明△AFG为等边三角形,从而可得出EF=EG+GF=AF+FC;
(3)在AF上截取AG=EF,连接BG,BF,证明方法类似(2),先证明△ABG≌△EBF,再证明△BFG为等边三角形,最后可得出结论.
解:(1)∵AB=AC,AD为BC边上的中线,∴可设∠BAD=∠CAD=α,
又△ABE为等边三角形,
∴AE=AB=AC,∠EAB=60°,∴可设∠AEC=∠ACE=β,
在△ACE中,2α+60°+2β=180°,
∴α+β=60°,
∴∠DFC=α+β=60°;
(2)EF=AF+FC,证明如下:
∵AB=AC,AD为BC边上的中线,∴AD⊥BC,∴∠FDC=90°,
∵∠CFD=60°,则∠DCF=30°,
∴CF=2DF,
在EC上截取EG=CF,连接AG,
又AE=AC,
∴∠AEG=∠ACF,
∴△AEG≌△ACF(SAS),
∴∠EAG=∠CAF,AG=AF,
又∠CAF=∠BAD,
∴∠EAG=∠BAD,
∴∠GAF=∠BAD+∠BAG=∠EAG+∠BAG=∠60°,
∴△AFG为等边三角形,
∴EF=EG+GF=AF+FC,
即EF=AF+FC;
(3)补全图形如图所示,
结论:AF=EF+2DF.证明如下:
同(1)可设∠BAD=∠CAD=α,∠ACE=∠AEC=β,
∴∠CAE=180°-2β,
∴∠BAE=2α+180°-2β=60°,∴β-α=60°,
∴∠AFC=β-α=60°,
又△ABE为等边三角形,∴∠ABE=∠AFC=60°,
∴由8字图可得:∠BAD=∠BEF,
在AF上截取AG=EF,连接BG,BF,
又AB=BE,
∴△ABG≌△EBF(SAS),
∴BG=BF,
又AF垂直平分BC,
∴BF=CF,
∴∠BFA=∠AFC=60°,
∴△BFG为等边三角形,
∴BG=BF,又BC⊥FG,∴FG=BF=2DF,
∴AF=AG+GF=BF+EF=2DF+EF.
【点睛】本题考查了全等三角形的判定和性质、等边三角形的性质、等腰三角形的性质等知识,解决问题的关键是常用辅助线构造全等三角形,属于中考常考题型.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
