华东师大版九年级上册23.3.2相似三角形的判定课件(共16张PPT)
文档属性
| 名称 | 华东师大版九年级上册23.3.2相似三角形的判定课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
华东师大版九年级上学期
第23章
《图形的相似》
学而不疑则怠,疑而不探则空
3.2
相似三角形的判定1
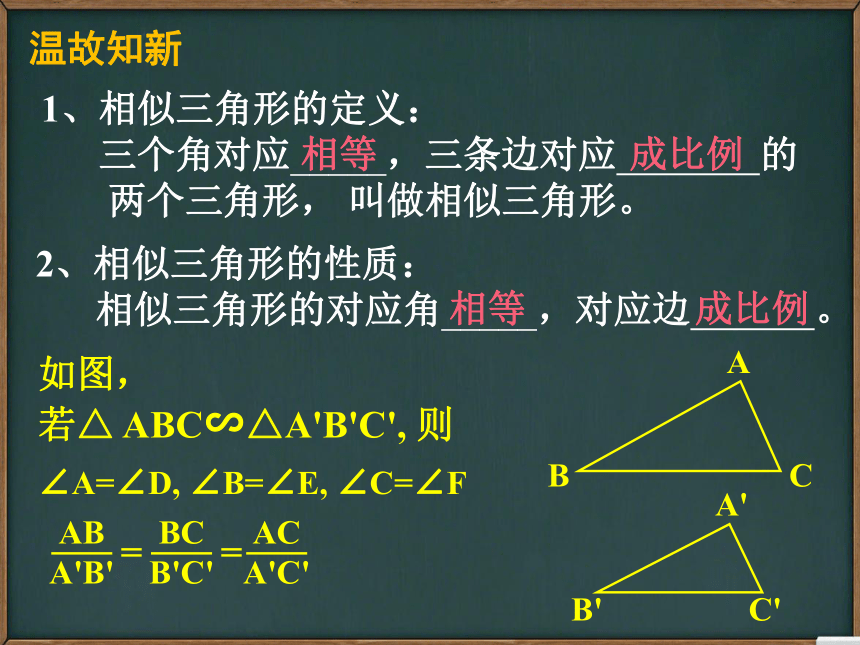
1、相似三角形的定义:
三个角对应_____,三条边对应
的
两个三角形,
叫做相似三角形。
相等
成比例
如图,
若△
ABC∽△A'B'C',
则
∠A=∠D,
∠B=∠E,
∠C=∠F
温故知新
2、相似三角形的性质:
相似三角形的对应角_____,对应边
。
相等
成比例
A
B
C
A'
B'
C'
AB
A'B'
=
BC
B'C'
=
AC
A'C'
思考:
1、判定两个三角形相似时,是不是对所有的
对应角和对应边都要一一验证呢?
不需要。类比全等三角形的判定可得。
知识探索
2、如果一个三角形的三个角分别与另一个
三角形的三个角对应相等,那么它们相似吗?
通过观察直角三角板,猜想:
三个角对应相等的两个三角形相似。
操作:
1、作两个三角形,使得三对角分别对应相等;
知识探索
85°
25°
70°
25°
70°
85°
2、测量对应边,并进行计算,看是否成比例.
归纳:
如果两个三角形三组对应角分别相等,
那么这两个三角形的对应边一定成比例。
知识探索
如果两个三角形两组对应角分别相等,
那么这两个三角形相似吗?
进而得:
如果两个三角形三组对应角分别相等,
那么这两个三角形一定相似。
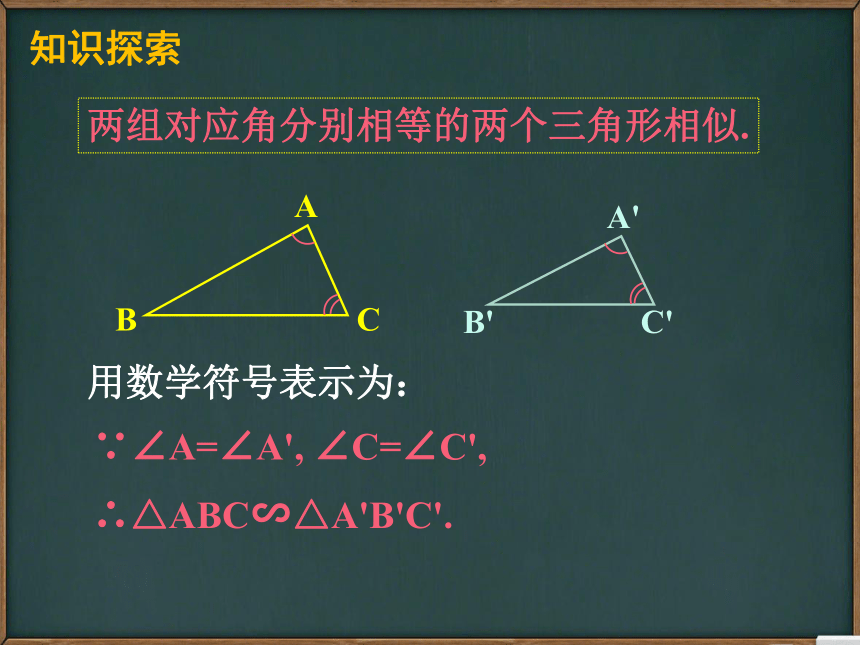
用数学符号表示为:
知识探索
两组对应角分别相等的两个三角形相似.
A
B
C
A'
B'
C'
∵∠A=∠A',
∠C=∠C',
∴△ABC∽△A'B'C'.
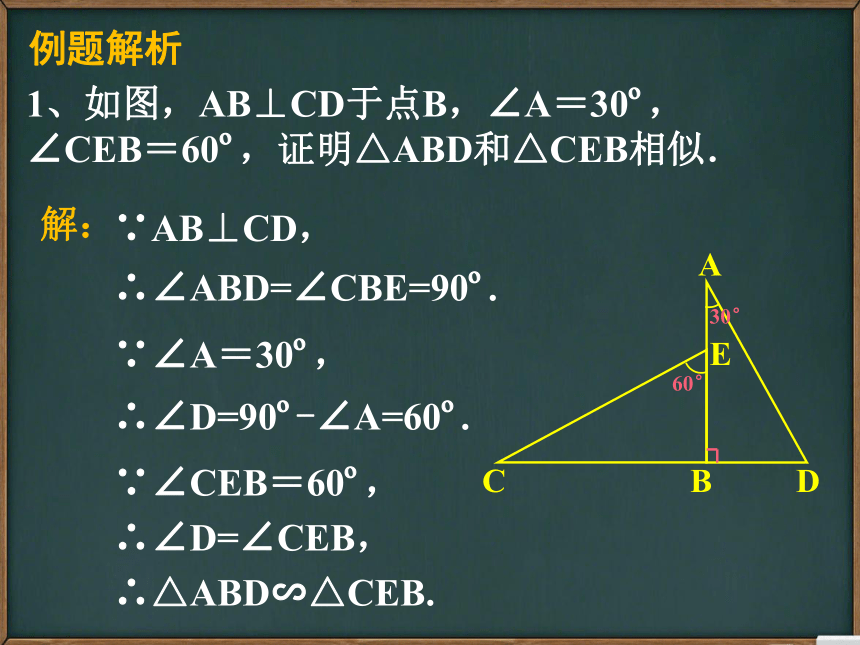
1、如图,AB⊥CD于点B,∠A=30?,
∠CEB=60?,证明△ABD和△CEB相似.
解:
∵AB⊥CD,
例题解析
A
60°
30°
E
C
B
D
∴∠ABD=∠CBE=90?.
∵∠A=30?,
∴∠D=90?-∠A=60?.
∵∠CEB=60?,
∴∠D=∠CEB,
∴△ABD∽△CEB.
2、如图,△ABC中,∠ABC=90?,BD⊥AC于点D,试找出图中一对相似的三角形并证明.
解:
∵BD⊥AC,
例题解析
B
A
D
C
∴∠BDC=90?.
∵∠ABC=90?,
∴∠ABC=∠BDC.
∵∠ACB=∠BCD,
∴△ABC∽△BDC.
△ABC∽△BDC.理由如下:
同理可得:
△ABC∽△ADB.
△BDC∽△ADB.
1、根据所给的条件,判断下列图形中的两个三角形是否相似:
练习反馈
A
73°
49°
C
B
M
73°
58°
N
P
C
57°
33°
D
E
O
P
Q
A
F
D
E
C
α
α
A
α
α
C
D
B
O
2、证明命题“平行三角形一边的直线截其余两边所在直线得到的三角形与原三角形相似”.
练习反馈
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
能否再简便一些?
有一对角对应相等的两个三角形相似吗?
交流探讨:
A
73°
C
B
M
73°
N
P
C
D
E
O
P
Q
不能!只有一对角对应相等,不能证明两个三角形相似。
3、如图,△ABC中,DE∥BC,EF∥AB,
证明:△ADE与△EFC相似.
证明:
∵DE∥BC,
例题解析
∴∠AED=∠C.
∵EF∥AB,
∴∠A=∠CEF.
∴△ADE∽△EFC.
证法二:由DE∥BC得△ADE∽△ABC,
由EF∥AB得△EFC∽△ABC,
由相似的传递性得△ADE∽△EFC.
A
B
C
D
E
F
1、判断下列命题是真命题还是假命题:
(1)
有一对角相等的两个三角形相似.
(2)
有一对锐角相等的两个直角三角形相似.
(3)
有一个角等于120?的两个等腰三角形相似.
(4)
有一个角等于50?的两个等腰三角形相似.
(5)
有一对角相等的两个等腰三角形相似.
(6)
等边三角形都相似.
练习反馈:
2、在下图1中,要得到△ACD∽△ABC,
写出需要添加的一个条件
。
A
B
C
D
3、在上图2中,要得到△AED与△ABC相似,
写出需要添加的一个条件
。
4、在上图3中,要得到△AOB∽△DOE,
写出需要添加的一个条件
。
A
B
D
C
E
A
B
D
O
E
通过本节课的学习,你掌握了什么知识?
课堂小结
用数学符号表示为:
两组对应角分别相等的两个三角形相似.
A
B
C
A'
B'
C'
∵∠A=∠A',
∠C=∠C',
∴△ABC∽△A'B'C'.
(AA)
课后思考
如图,△ABC中,DE∥BC,若点D
是AB的中点,
(1)证明:点E是AC的中点;
(2)DE和BC是什么关系?
(3)若点F是BC的中点,连接EF、DF,
△DEF和△ABC是什么关系?
A
B
C
D
E
华东师大版九年级上学期
第23章
《图形的相似》
学而不疑则怠,疑而不探则空
3.2
相似三角形的判定1
1、相似三角形的定义:
三个角对应_____,三条边对应
的
两个三角形,
叫做相似三角形。
相等
成比例
如图,
若△
ABC∽△A'B'C',
则
∠A=∠D,
∠B=∠E,
∠C=∠F
温故知新
2、相似三角形的性质:
相似三角形的对应角_____,对应边
。
相等
成比例
A
B
C
A'
B'
C'
AB
A'B'
=
BC
B'C'
=
AC
A'C'
思考:
1、判定两个三角形相似时,是不是对所有的
对应角和对应边都要一一验证呢?
不需要。类比全等三角形的判定可得。
知识探索
2、如果一个三角形的三个角分别与另一个
三角形的三个角对应相等,那么它们相似吗?
通过观察直角三角板,猜想:
三个角对应相等的两个三角形相似。
操作:
1、作两个三角形,使得三对角分别对应相等;
知识探索
85°
25°
70°
25°
70°
85°
2、测量对应边,并进行计算,看是否成比例.
归纳:
如果两个三角形三组对应角分别相等,
那么这两个三角形的对应边一定成比例。
知识探索
如果两个三角形两组对应角分别相等,
那么这两个三角形相似吗?
进而得:
如果两个三角形三组对应角分别相等,
那么这两个三角形一定相似。
用数学符号表示为:
知识探索
两组对应角分别相等的两个三角形相似.
A
B
C
A'
B'
C'
∵∠A=∠A',
∠C=∠C',
∴△ABC∽△A'B'C'.
1、如图,AB⊥CD于点B,∠A=30?,
∠CEB=60?,证明△ABD和△CEB相似.
解:
∵AB⊥CD,
例题解析
A
60°
30°
E
C
B
D
∴∠ABD=∠CBE=90?.
∵∠A=30?,
∴∠D=90?-∠A=60?.
∵∠CEB=60?,
∴∠D=∠CEB,
∴△ABD∽△CEB.
2、如图,△ABC中,∠ABC=90?,BD⊥AC于点D,试找出图中一对相似的三角形并证明.
解:
∵BD⊥AC,
例题解析
B
A
D
C
∴∠BDC=90?.
∵∠ABC=90?,
∴∠ABC=∠BDC.
∵∠ACB=∠BCD,
∴△ABC∽△BDC.
△ABC∽△BDC.理由如下:
同理可得:
△ABC∽△ADB.
△BDC∽△ADB.
1、根据所给的条件,判断下列图形中的两个三角形是否相似:
练习反馈
A
73°
49°
C
B
M
73°
58°
N
P
C
57°
33°
D
E
O
P
Q
A
F
D
E
C
α
α
A
α
α
C
D
B
O
2、证明命题“平行三角形一边的直线截其余两边所在直线得到的三角形与原三角形相似”.
练习反馈
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
能否再简便一些?
有一对角对应相等的两个三角形相似吗?
交流探讨:
A
73°
C
B
M
73°
N
P
C
D
E
O
P
Q
不能!只有一对角对应相等,不能证明两个三角形相似。
3、如图,△ABC中,DE∥BC,EF∥AB,
证明:△ADE与△EFC相似.
证明:
∵DE∥BC,
例题解析
∴∠AED=∠C.
∵EF∥AB,
∴∠A=∠CEF.
∴△ADE∽△EFC.
证法二:由DE∥BC得△ADE∽△ABC,
由EF∥AB得△EFC∽△ABC,
由相似的传递性得△ADE∽△EFC.
A
B
C
D
E
F
1、判断下列命题是真命题还是假命题:
(1)
有一对角相等的两个三角形相似.
(2)
有一对锐角相等的两个直角三角形相似.
(3)
有一个角等于120?的两个等腰三角形相似.
(4)
有一个角等于50?的两个等腰三角形相似.
(5)
有一对角相等的两个等腰三角形相似.
(6)
等边三角形都相似.
练习反馈:
2、在下图1中,要得到△ACD∽△ABC,
写出需要添加的一个条件
。
A
B
C
D
3、在上图2中,要得到△AED与△ABC相似,
写出需要添加的一个条件
。
4、在上图3中,要得到△AOB∽△DOE,
写出需要添加的一个条件
。
A
B
D
C
E
A
B
D
O
E
通过本节课的学习,你掌握了什么知识?
课堂小结
用数学符号表示为:
两组对应角分别相等的两个三角形相似.
A
B
C
A'
B'
C'
∵∠A=∠A',
∠C=∠C',
∴△ABC∽△A'B'C'.
(AA)
课后思考
如图,△ABC中,DE∥BC,若点D
是AB的中点,
(1)证明:点E是AC的中点;
(2)DE和BC是什么关系?
(3)若点F是BC的中点,连接EF、DF,
△DEF和△ABC是什么关系?
A
B
C
D
E
