人教版七年级上册数学 4.3角 同步练习(word版含解析)
文档属性
| 名称 | 人教版七年级上册数学 4.3角 同步练习(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 87.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 00:00:00 | ||
图片预览



文档简介
4.3角 同步练习
一.选择题
1.如图OA为北偏东30°方向,∠AOB=90°,则OB的方向为( )
A.南偏东60° B.南偏东30° C.南偏西60° D.东偏北60°
2.若∠A=38°15′,∠B=38.15°,则( )
A.∠A>∠B B.∠A<∠B C.∠A=∠B D.无法确定
3.11点40分,时钟的时针与分针的夹角为( )
A.140° B.130° C.120° D.110°
4.如图所示的是正方形网格,则∠AOB___∠COD( )
A.> B.< C.= D.≥
5.一个角的余角是44°,这个角的补角是( )
A.134° B.136° C.156° D.146°
6.下列叙述正确的是( )
A.一个钝角和一个锐角一定互为补角
B.每一个锐角都有余角
C.两个锐角一定互为余角
D.一个钝角的余角是锐角
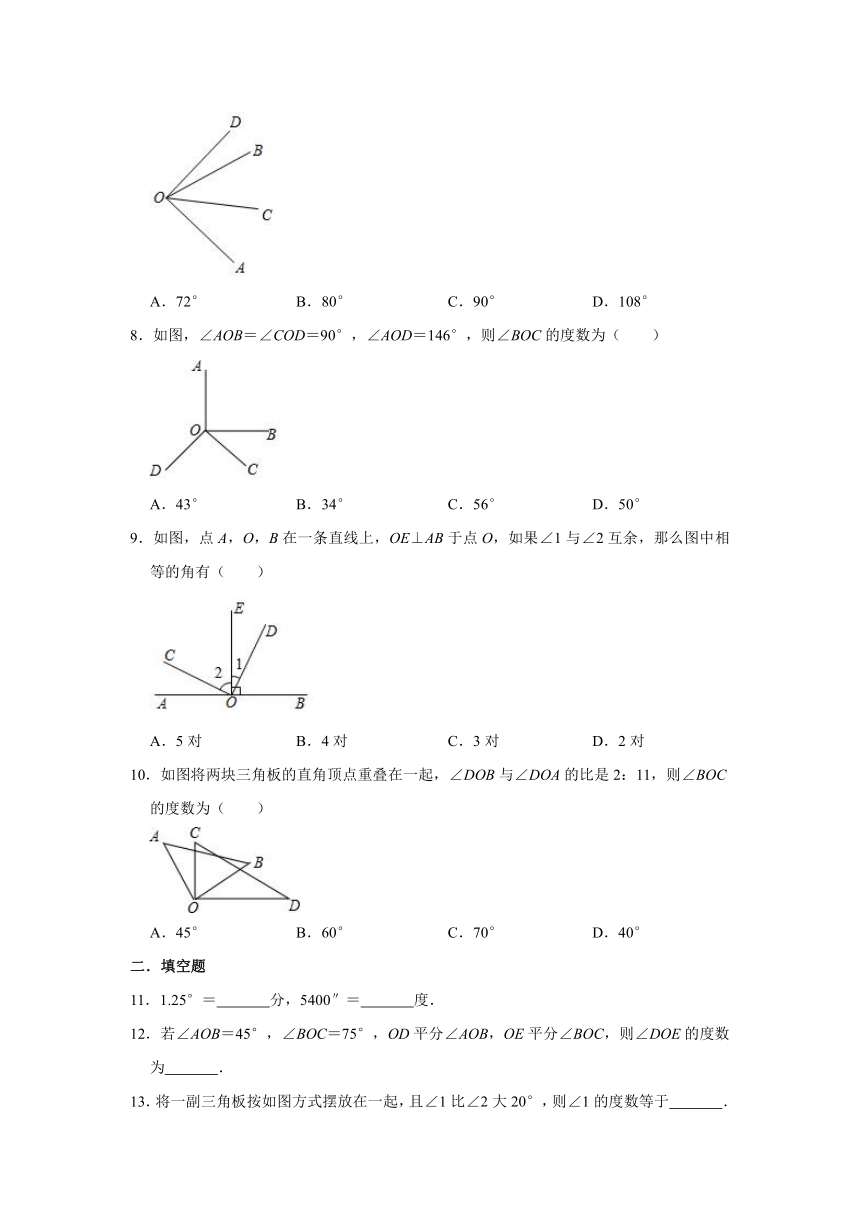
7.如图,OC是∠AOB的平分线,∠BOD=∠DOC,∠BOD=18°,则∠AOD的度数为( )
A.72° B.80° C.90° D.108°
8.如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC的度数为( )
A.43° B.34° C.56° D.50°
9.如图,点A,O,B在一条直线上,OE⊥AB于点O,如果∠1与∠2互余,那么图中相等的角有( )
A.5对 B.4对 C.3对 D.2对
10.如图将两块三角板的直角顶点重叠在一起,∠DOB与∠DOA的比是2:11,则∠BOC的度数为( )
A.45° B.60° C.70° D.40°
二.填空题
11.1.25°= 分,5400″= 度.
12.若∠AOB=45°,∠BOC=75°,OD平分∠AOB,OE平分∠BOC,则∠DOE的度数为 .
13.将一副三角板按如图方式摆放在一起,且∠1比∠2大20°,则∠1的度数等于 .
14.若∠A与∠B互为余角,∠A=30°,则∠B的补角是 度.
15.已知∠AOB=80°,在∠AOB内部作射线OC,若射线OM平分∠AOC,射线ON平分∠BOC,则∠MON的度数为 .
三.解答题
16.如图,已知∠AOB=128°,OC平分∠AOB,请你在∠COB内部画射线OD,使∠COD和∠AOC互余,并求∠COD的度数.
17.如图所示,O为直线上的一点,且∠COD为直角,OE平分∠BOD,OF平分∠AOE,∠BOC+∠FOD=117°,求∠BOE的度数.
18.如图所示,已知BC是从直线AB上出发的一条射线,BE平分∠ABC,∠EBF=90°.求证:BF平分∠CBD.
参考答案
1.解:如图所示:
∵OA是北偏东30°方向的一条射线,∠AOB=90°,
∴∠1=30°,
∴∠2=60°,
∴OB的方向角是南偏东60°.
故选:A.
2.解:∵∠A=38°15′,∠B=38.15°=38°9′,
∴∠A>∠B.
故选:A.
3.解:11点40分时针与分针相距3+=(份),
30°×=110°,
故选:D.
4.解:∵∠AOC=∠BOD=90°,
∴∠AOB+∠BOC=90°,∠COD+∠BOC=90°,
∴∠AOB=∠COD.
故选:C.
5.解:∵一个角的余角是44°,
∴这个角的度数是:90°﹣44°=46°,
∴这个角的补角是:180°﹣46°=134°.
故选:A.
6.解:A.一个锐角与一个钝角不一定互为补角,故本选项错误;
B.每一个锐角都有余角,故本选项正确;
C.只有两个锐角的和为90°时,这两个角才互余,故原说法错误;
D.钝角的没有余角,故此选项错误;
故选:B.
7.解:设∠DOB=k,
∵∠BOD=∠DOC,
∴∠BOC=2k,
∵OC是∠AOB的平分线,
∴∠COA=∠BOC=2k,
∴∠AOD=∠DOB+∠BOC+∠COA=5k,
∵∠BOD=18°,
∴∠AOD=5×18°=90°,
故选:C.
8.解:∠AOB=∠COD=90°,∠AOD=146°
则∠BOC=360°﹣2×90°﹣146°=34°
则∠BOC=34°.
故选:B.
9.解:∵OE⊥AB,
∴∠AOE=∠BOE=90°,
∵∠1与∠2互余,
∴∠1+∠2=90°,
∴∠1=∠AOC,
∠2=∠BOD,
∠AOE=∠COD,
∠BOE=∠COD,
∴图中相等的角有5对.
故选:A.
10.解:设∠DOB为2x,∠DOA为11x;
∴∠AOB=∠DOA﹣∠DOB=9x,
∵∠AOB=90°,
∴9x=90°,
∴x=10°,
∴∠DOB=20°,
∴∠BOC=∠COD﹣∠DOB=90°﹣20°=70°;
故选:C.
11.解:1.25°=1×60′+0.25×60′=60′+15′=75′,
5400″=(5400÷60)′=90′=(90÷60)°=1.5°,
故答案为:75;1.5.
12.解:如图1,
∵∠AOB=45°,
∴∠BOD=22.5°,
∵∠BOC=75°,
∴∠BOE=37.5°,
∴∠DOE=22.5°+37.5°=60°;
如图2,∵∠AOB=45°,
∴∠BOD=22.5°,
∵∠BOC=75°,
∴∠BOE=37.5°,
∴∠DOE=37.5°﹣22.5°=15°,
故答案为:60°或15°.
13.解:设∠2为x,则∠1=x+20°;根据题意得:
x+x+20°=90°,
解得:x=35°,
则∠1=35°+20°=55°;
故答案为:55°.
14.解:∠A与∠B互为余角,∠A=30°,
则∠B=60°;
则∠B的补角=120°.
故答案为:120.
15.解:如图,
∵射线OM平分∠AOC,射线ON平分∠BOC,
∴∠MOC=∠AOC,∠NOC=∠BOC,
∵∠AOC+∠BOC=∠AOB=80°,
∴∠MOC+∠NOC=(∠AOC+∠BOC)=∠AOB=40°,
∵∠MON=∠MOC+∠NOC,
∴∠MON=40°.
故答案为40°.
16.解:作OD⊥OA,则∠COD和∠AOC互余,如图所示.
∵∠AOB=128°,OC平分∠AOB,
∴∠AOC=∠AOB=64°,
∵∠COD和∠AOC互余,
∴∠COD=90°﹣∠AOC=26°.
17.解:设∠BOE=α°,
∵OE平分∠BOD,
∴∠BOD=2α°,∠EOD=α°.
∵∠COD=∠BOD+∠BOC=90°,
∴∠BOC=90°﹣2α°.
∵OF平分∠AOE,∠AOE+∠BOE=180°,
∴∠FOE=∠AOE=(180°﹣α°)=90°﹣α°,
∴∠FOD=∠FOE﹣∠EOD=90°﹣α°﹣α°=90°﹣α°,
∵∠BOC+∠FOD=117°,
∴90°﹣2α°+90°﹣α°=117°,
∴α=18,
∴∠BOE=18°.
18.证明:∵BE平分∠ABC,
∴∠CBE=∠ABE,
∵∠EBF=90°,
∴∠CBF=90°﹣∠CBE,
∴∠DBF=180°﹣90°﹣∠ABE=90°﹣∠CBE=∠CBF.
即BF平分∠CBD.
一.选择题
1.如图OA为北偏东30°方向,∠AOB=90°,则OB的方向为( )
A.南偏东60° B.南偏东30° C.南偏西60° D.东偏北60°
2.若∠A=38°15′,∠B=38.15°,则( )
A.∠A>∠B B.∠A<∠B C.∠A=∠B D.无法确定
3.11点40分,时钟的时针与分针的夹角为( )
A.140° B.130° C.120° D.110°
4.如图所示的是正方形网格,则∠AOB___∠COD( )
A.> B.< C.= D.≥
5.一个角的余角是44°,这个角的补角是( )
A.134° B.136° C.156° D.146°
6.下列叙述正确的是( )
A.一个钝角和一个锐角一定互为补角
B.每一个锐角都有余角
C.两个锐角一定互为余角
D.一个钝角的余角是锐角
7.如图,OC是∠AOB的平分线,∠BOD=∠DOC,∠BOD=18°,则∠AOD的度数为( )
A.72° B.80° C.90° D.108°
8.如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC的度数为( )
A.43° B.34° C.56° D.50°
9.如图,点A,O,B在一条直线上,OE⊥AB于点O,如果∠1与∠2互余,那么图中相等的角有( )
A.5对 B.4对 C.3对 D.2对
10.如图将两块三角板的直角顶点重叠在一起,∠DOB与∠DOA的比是2:11,则∠BOC的度数为( )
A.45° B.60° C.70° D.40°
二.填空题
11.1.25°= 分,5400″= 度.
12.若∠AOB=45°,∠BOC=75°,OD平分∠AOB,OE平分∠BOC,则∠DOE的度数为 .
13.将一副三角板按如图方式摆放在一起,且∠1比∠2大20°,则∠1的度数等于 .
14.若∠A与∠B互为余角,∠A=30°,则∠B的补角是 度.
15.已知∠AOB=80°,在∠AOB内部作射线OC,若射线OM平分∠AOC,射线ON平分∠BOC,则∠MON的度数为 .
三.解答题
16.如图,已知∠AOB=128°,OC平分∠AOB,请你在∠COB内部画射线OD,使∠COD和∠AOC互余,并求∠COD的度数.
17.如图所示,O为直线上的一点,且∠COD为直角,OE平分∠BOD,OF平分∠AOE,∠BOC+∠FOD=117°,求∠BOE的度数.
18.如图所示,已知BC是从直线AB上出发的一条射线,BE平分∠ABC,∠EBF=90°.求证:BF平分∠CBD.
参考答案
1.解:如图所示:
∵OA是北偏东30°方向的一条射线,∠AOB=90°,
∴∠1=30°,
∴∠2=60°,
∴OB的方向角是南偏东60°.
故选:A.
2.解:∵∠A=38°15′,∠B=38.15°=38°9′,
∴∠A>∠B.
故选:A.
3.解:11点40分时针与分针相距3+=(份),
30°×=110°,
故选:D.
4.解:∵∠AOC=∠BOD=90°,
∴∠AOB+∠BOC=90°,∠COD+∠BOC=90°,
∴∠AOB=∠COD.
故选:C.
5.解:∵一个角的余角是44°,
∴这个角的度数是:90°﹣44°=46°,
∴这个角的补角是:180°﹣46°=134°.
故选:A.
6.解:A.一个锐角与一个钝角不一定互为补角,故本选项错误;
B.每一个锐角都有余角,故本选项正确;
C.只有两个锐角的和为90°时,这两个角才互余,故原说法错误;
D.钝角的没有余角,故此选项错误;
故选:B.
7.解:设∠DOB=k,
∵∠BOD=∠DOC,
∴∠BOC=2k,
∵OC是∠AOB的平分线,
∴∠COA=∠BOC=2k,
∴∠AOD=∠DOB+∠BOC+∠COA=5k,
∵∠BOD=18°,
∴∠AOD=5×18°=90°,
故选:C.
8.解:∠AOB=∠COD=90°,∠AOD=146°
则∠BOC=360°﹣2×90°﹣146°=34°
则∠BOC=34°.
故选:B.
9.解:∵OE⊥AB,
∴∠AOE=∠BOE=90°,
∵∠1与∠2互余,
∴∠1+∠2=90°,
∴∠1=∠AOC,
∠2=∠BOD,
∠AOE=∠COD,
∠BOE=∠COD,
∴图中相等的角有5对.
故选:A.
10.解:设∠DOB为2x,∠DOA为11x;
∴∠AOB=∠DOA﹣∠DOB=9x,
∵∠AOB=90°,
∴9x=90°,
∴x=10°,
∴∠DOB=20°,
∴∠BOC=∠COD﹣∠DOB=90°﹣20°=70°;
故选:C.
11.解:1.25°=1×60′+0.25×60′=60′+15′=75′,
5400″=(5400÷60)′=90′=(90÷60)°=1.5°,
故答案为:75;1.5.
12.解:如图1,
∵∠AOB=45°,
∴∠BOD=22.5°,
∵∠BOC=75°,
∴∠BOE=37.5°,
∴∠DOE=22.5°+37.5°=60°;
如图2,∵∠AOB=45°,
∴∠BOD=22.5°,
∵∠BOC=75°,
∴∠BOE=37.5°,
∴∠DOE=37.5°﹣22.5°=15°,
故答案为:60°或15°.
13.解:设∠2为x,则∠1=x+20°;根据题意得:
x+x+20°=90°,
解得:x=35°,
则∠1=35°+20°=55°;
故答案为:55°.
14.解:∠A与∠B互为余角,∠A=30°,
则∠B=60°;
则∠B的补角=120°.
故答案为:120.
15.解:如图,
∵射线OM平分∠AOC,射线ON平分∠BOC,
∴∠MOC=∠AOC,∠NOC=∠BOC,
∵∠AOC+∠BOC=∠AOB=80°,
∴∠MOC+∠NOC=(∠AOC+∠BOC)=∠AOB=40°,
∵∠MON=∠MOC+∠NOC,
∴∠MON=40°.
故答案为40°.
16.解:作OD⊥OA,则∠COD和∠AOC互余,如图所示.
∵∠AOB=128°,OC平分∠AOB,
∴∠AOC=∠AOB=64°,
∵∠COD和∠AOC互余,
∴∠COD=90°﹣∠AOC=26°.
17.解:设∠BOE=α°,
∵OE平分∠BOD,
∴∠BOD=2α°,∠EOD=α°.
∵∠COD=∠BOD+∠BOC=90°,
∴∠BOC=90°﹣2α°.
∵OF平分∠AOE,∠AOE+∠BOE=180°,
∴∠FOE=∠AOE=(180°﹣α°)=90°﹣α°,
∴∠FOD=∠FOE﹣∠EOD=90°﹣α°﹣α°=90°﹣α°,
∵∠BOC+∠FOD=117°,
∴90°﹣2α°+90°﹣α°=117°,
∴α=18,
∴∠BOE=18°.
18.证明:∵BE平分∠ABC,
∴∠CBE=∠ABE,
∵∠EBF=90°,
∴∠CBF=90°﹣∠CBE,
∴∠DBF=180°﹣90°﹣∠ABE=90°﹣∠CBE=∠CBF.
即BF平分∠CBD.
