北师大版八年级数学上册第三章位置与坐标同步能力测试题(Word版,答案不全)
文档属性
| 名称 | 北师大版八年级数学上册第三章位置与坐标同步能力测试题(Word版,答案不全) |

|
|
| 格式 | docx | ||
| 文件大小 | 357.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 00:00:00 | ||
图片预览




文档简介
北师版八年级数学上册
第三章能力测试题含答案3.1确定位置
一、选择题(共10小题,3
10=30)
1.海事救灾船前去救援某海域失火轮船需要确定(
)
A.方位
B.距离
C.方位和距离
D.失火轮船的国籍
2.北京时间某年5月24日4时49分云南省德宏傣族景颇族自治州盈江县(北纬25.0°,东经97.8°)发生5.6级地震,能够准确表述这个地点位置的是(
)
A.北纬25.0°
B.东经97.8°
C.云南西部
D.北纬25.0°,东经97.8°
3.到电影院看电影需要对号入座,那么“对号入座”的意思是(
)
A.在电影院里随便找个座位坐下即可
B.在电影院里只要找到座位号即可
C.在电影院里只要找到排号即可
D.在电影院里既要找到排号,又要找到座位号
4.小强向同学们介绍图书馆的位置时,其中表达准确的是(
)
A.在学校的右边
B.距学校1
000米
C.在学校的西边
D.在学校的西边距学校1
000米处
5.老师对班上的同学的座位进行调整,下面说法能找到座位的是(
)
A.3排4列
B.从前数第3排4列
C.3排从左数第4列
D.从前数第3排,从左数第4列
6.
若我军战舰攻打敌军战舰,需要知道(
)
A.我军战舰的位置
B.敌军战舰相对于我军战舰的方向
C.敌军战舰相对于我军战舰的距离
D.敌军战舰相对于我军战舰的方向和距离
7.钓鱼岛历来就是中国不可分割的领土,中国对钓鱼岛及其附近海域拥有无可争辩的主权,能够准确表示钓鱼岛位置的是( )
A.北纬25°40′~26°
B.东经123°~124°34′
C.福建的正东方向
D.东经123°~124°34′,北纬25°40′~26°
8.七年级(2)班有45人参加学校运动会的入场仪式,队伍共有9排5列.如果用(2,4)表示第2排从左至右第4列的同学,那么第4排从左至右第6列的同学表示为( )
A.(4,10)
B.(4,6)
C.(10,6)
D.(6,4)
9.如图,有两种关于A,B两地位置关系的描述:
①B在A北偏东70°方向,与A相距100
m;
②A在B南偏西70°方向,与B相距100
m.
下列判断正确的是( )
A.①对②错
B.①对②对
C.①错②对
D.①错②错
10.如图是沈阳地区简图的一部分,图中“故宫”“鼓楼”所在的区域分别是( )
A.D7,E6
B.D6,E7
C.E7,D6
D.E6,D7
二.填空题(共8小题,3
8=24)
11.有人在市中心打听第一中学的位置,问了三个人,得到三种不同的回答:①在市中心的西北方向;②距市中心1
km;③在市中心的西北方向,距市中心1
km处.在上述回答中能确定第一中学位置的是__________.(填序号)
12.
课间操时,小华、小军、小刚的位置如图,小华的位置用(0,0)表示,小军的位置用(2,1)表示,那么小刚的位置可以表示成________.
13.如图是在方格纸上画出的小旗图案,若用(0,0)表示点A,(0,4)表示点B,那么点C的位置可表示为________.
14.如图所示,某班教室有9排5列座位.1号同学说:“小明在我的右后方.”2号同学说:“小明在我的左后方.”3号同学说:“小明在我的左前方.”4号同学说:“小明离1号同学和3号同学的距离一样远.”根据上面4位同学的描述,可知“5号”小明的位置在________.
15.如果电影票上的“5排2号”记作(5,2),那么(4,3)表示____________.
16..如图是小明所在学校的示意图,学校大门位于从左数第5条纵向网格线与从下数第1条横向网格线的交点上,它的位置表示为(5,1),则实验楼的位置表示为
___________,____的位置表示为(7,5).
17.如图,已知A(-2,1),B(-6,0),若白棋A飞挂后,黑棋C尖顶,黑棋C可以表示为(______,______).
18.如图,雷达探测器测得六个目标点A,B,C,D,E,F出现,按照规定的目标表示方法,目标点C,F的位置表示为C(6,120°),F(5,210°),按照此方法在表示目标点A,B,D的位置是_______________________________________.
三.解答题(共7小题,
46分)
19.(6分)
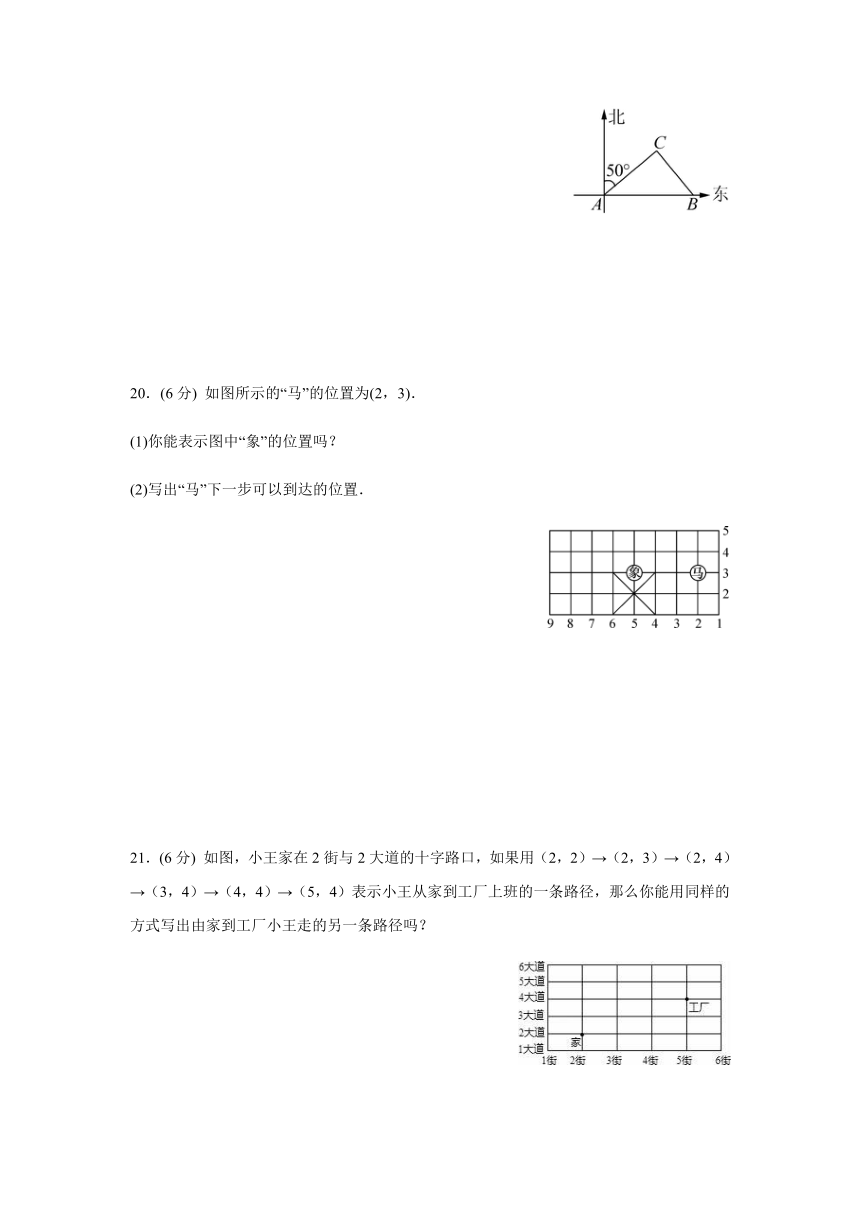
如图,某港口有一灯塔A,灯塔A的正东方向有一个小岛B,从灯塔A处看到在它的北偏东50°方向上有一艘轮船C.
(1)要确定轮船C的位置还需要哪些数据?
(2)从轮船C看灯塔A用怎样的方位角来表示?
20.(6分)
如图所示的“马”的位置为(2,3).
(1)你能表示图中“象”的位置吗?
(2)写出“马”下一步可以到达的位置.
21.(6分)
如图,小王家在2街与2大道的十字路口,如果用(2,2)→(2,3)→(2,4)→(3,4)→(4,4)→(5,4)表示小王从家到工厂上班的一条路径,那么你能用同样的方式写出由家到工厂小王走的另一条路径吗?
22.(6分)
如图,点A表示2街与4大道的十字路口,记为(2,4);点B表示4街与2大道的十字路口,记为(4,2).例如,可以用(2,4)→(2,3)→(3,3)→(4,3)→(4,2)表示从点A到点B的路径.
(1)请你用同样的方法写出其他两种表示从点A到点B的路径:
①__________________________________________________;
②__________________________________________________.
(2)请探究:从点A到点B的最短路径共有__________条.
23.(6分)
如图,请设计一条由学校到博物馆的路线,并分别用“××区(例如A3区)”表示这条路线所经过的区域.
24.(8分)
一次,小红在寄给小伙伴的信中附加了一张自己学校周边环境的示意图来介绍自己学校的位置及情况(如图),对于学校来说,
(1)正东方向上有哪些设施?要明确这些设施相对于学校的位置,还需要知道哪些数据?
(2)离学校最近的设施是什么?在学校的哪个方向上?这一方向上还有其他设施吗?怎样区分?
(3)要确定电视塔相对于学校的位置,需要知道哪些数据?
25.(8分)
如图,一只甲虫在10×10的方格(每个小方格的边长为1)纸上沿着网格线运动,它从C处出发想去看望A,B,D,E处的其他甲虫,规定:向下向左走为正,向上向右走为负.则从C到B记为C→B(+5,+2)(第一个数表示左、右方向,第二个数表示上、下方向).
(1)填空:C→D(____,____);C→A(____,____);D→____(+5,-6);E→____(____,-4).
(2)若这只甲虫的行走路线是C→A→B→D→E,请计算该甲虫走过的路程.
(3)这只甲虫从C处出发去另一只甲虫家P处的行走路线依次为(-2,+2),(+3,-4),(-4,+2),(+7,+3),请在图上描出这只甲虫的行走路线并标出P点的位置,想一想,有没有简便的方法?
参考答案
1-5CDDDD
6-10DDBBC
11.
③
12.
(4,3)
13.
(3,2)
14.
5排4列
15.
3排4号
16.
(3,7),操场
-1,1
18.
(5,30°)
,(2,90°),(4,240°)
19.
解:(1)点C到点A的距离
(2)灯塔A在轮船C的南偏西50°方向上
20.
解:(1)“象”的位置为(5,3)
(2)“马”的下一步可以到达的位置为(1,1),(3,1),(4,2),(1,5),(3,5),(4,4)
21.
解:小王从家到工厂上班的另一条路径可为:(2,2)→(3,2)→(4,2)→(5,2)→(5,3)→(5,4).
22.
解:(1)
(答案不唯一)(2,4)→(2,3)→(2,2)→(3,2)→(4,2)
(2,4)→(3,4)→(4,4)→(4,3)→(4,2)
(2)6
23.
解:路线:A4区→A3区→A2区→B2区→C2区→C1区→D1区→D2区.(答案不唯一)
24.
解:(1)正东方向上有超市和艺术中心,要明确这些设施相对于学校的位置,还需要知道它们与学校的距离.
(2)离学校最近的设施是儿童公园,它在学校南偏西30°的方向上;这一方向上还有农贸市场;它们与学校的距离不同.
(3)要确定电视塔相对于学校的位置,需要知道它的方位角和距离.
25.
解:(1)+2,+4,+7,-2,A,D,+5
(2)7+2+2+4+3+2+5+4=29.
(3)如图,简便方法:所行走路线的第一个数与第二个数分别相加,所得结果即为C到P的行走路线,即C→P(+4,+3).
3.2
平面直角坐标系
一、选择题(共8小题,每小题3分,满分24分)
1.已知点P位于x轴上方,距离x轴4个单位长度,位于y轴右侧,距y轴3个单位长度,则点P坐标是( )
A.(﹣3,4)
B.(﹣4,3)
C.(3,4)
D.(4,3)
2.已知在直角坐标系中有点P(x、y),且x、y满足条件|x|=5,|x﹣y|=8,则这样的点P有( )
A.1个
B.2个
C.4个
D.8个
3.第二象限内一点P到x轴的距离等于2,到y轴的距离等于3,则点P的坐标为( )
A.(﹣2,3)
B.(2,﹣3)
C.(﹣3,2)
D.(3,﹣2)
4.已知点P到x轴的距离为1,到y轴的距离为2,则点P的坐标不可能为( )
A.(1,2)
B.(﹣2,﹣1)
C.(2,﹣1)
D.(2,1)
5.在平面直角坐标系中,点(﹣5,2)所在的象限为( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.如果点P(m+3,m+1)在x轴上,则点P的坐标为( )
A.(0,2)
B.(2,0)
C.(4,0)
D.(0,﹣4)
7.正方形的两条边在坐标轴上,其中一个顶点的坐标是(0,0),其他部分在第三象限,面积为4,那么这个正方形不在坐标轴上的顶点的坐标是( )
A.(2,2)
B.(﹣2,﹣2)
C.(﹣2,2)
D.(2,﹣2)
8.在第二象限内,到x轴距离为3,到y轴距离为2的点P坐标为( )
A.(3,2)
B.(2,3)
C.(﹣3,2)
D.(﹣2,3)
二、填空题(共5小题,每小题3分,满分15分)
9.在y轴上,若点M与点N(0,3)的距离是6,则点M的坐标是
.
10.在x轴上,若点P与点Q(﹣2,0)的距离是5,则点P的坐标是
.
11.平面上有一点P(a,b),点P到x轴、y轴的距离分别为3、4,且ab<0,则点P的坐标是
.
12.点P(m+3,m+1)在直角坐标系的x轴上,则P点坐标为
.
13.若点M(a﹣3,a+4)在y轴上,则M点的坐标为
.
三、解答题(共1小题,满分0分)
14.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点P到x轴、y轴的距离相等;
(4)点Q的坐标为(1,5),直线PQ∥y轴.
参考答案与试题解析
一、选择题(共8小题,每小题3分,满分24分)
1.已知点P位于x轴上方,距离x轴4个单位长度,位于y轴右侧,距y轴3个单位长度,则点P坐标是( )
A.(﹣3,4)
B.(﹣4,3)
C.(3,4)
D.(4,3)
【分析】根据题意,P点应在第一象限,横、纵坐标为正,再根据P点到坐标轴的距离确定点的坐标.
【解答】解:∵P点位于y轴右侧,x轴上方,
∴P点在第一象限,
又∵P点距y轴3个单位长度,距x轴4个单位长度,
∴P点横坐标为3,纵坐标为4,即点P的坐标为(3,4).
故选:C.
2.已知在直角坐标系中有点P(x、y),且x、y满足条件|x|=5,|x﹣y|=8,则这样的点P有( )
A.1个
B.2个
C.4个
D.8个
【分析】根据题意,由|x|=5可得,x=±5,又由|x﹣y|=8,即x﹣y=±8,代入x的值,解可得y的值,进而可得解的组数,即可得答案.
【解答】解:根据题意,
由|x|=5可得,x=±5,
又由|x﹣y|=8,即x﹣y=±8,
当x=5时,可得y=13或﹣3,
当x=﹣5时,可得y=﹣13或3,
即这样的点P有4个,分别为(5,﹣3),(5,13),(﹣5,3),(﹣5,﹣13);
故选:C.
3.第二象限内一点P到x轴的距离等于2,到y轴的距离等于3,则点P的坐标为( )
A.(﹣2,3)
B.(2,﹣3)
C.(﹣3,2)
D.(3,﹣2)
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值解答即可.
【解答】解:∵第二象限内一点P到x轴的距离等于2,到y轴的距离等于3,
∴点P的横坐标为﹣3,纵坐标为2,
∴点P的坐标为(﹣3,2).
故选:C.
4.已知点P到x轴的距离为1,到y轴的距离为2,则点P的坐标不可能为( )
A.(1,2)
B.(﹣2,﹣1)
C.(2,﹣1)
D.(2,1)
【分析】根据点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度求出点P可能的横坐标与纵坐标,即可得解.
【解答】解:∵点P到x轴的距离为1,到y轴的距离为2,
∴点P的横坐标为2或﹣2,纵坐标为1或﹣1,
∴点P的坐标不可能为(1,2).
故选:A.
5.在平面直角坐标系中,点(﹣5,2)所在的象限为( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
【分析】根据各象限内点的坐标特征解答即可.
【解答】解:点(﹣5,2)在第二象限.
故选:B.
6.如果点P(m+3,m+1)在x轴上,则点P的坐标为( )
A.(0,2)
B.(2,0)
C.(4,0)
D.(0,﹣4)
【分析】根据点P在x轴上,即y=0,可得出m的值,从而得出点P的坐标.
【解答】解:∵点P(m+3,m+1)在x轴上,
∴y=0,
∴m+1=0,
解得:m=﹣1,
∴m+3=﹣1+3=2,
∴点P的坐标为(2,0).
故选:B.
7.正方形的两条边在坐标轴上,其中一个顶点的坐标是(0,0),其他部分在第三象限,面积为4,那么这个正方形不在坐标轴上的顶点的坐标是( )
A.(2,2)
B.(﹣2,﹣2)
C.(﹣2,2)
D.(2,﹣2)
【分析】根据正方形的性质即可得这个正方形不在坐标轴上的顶点的坐标.
【解答】解:因为正方形的面积为4,
所以正方形的边长为2,
因为正方形的两条边在坐标轴上,其中一个顶点的坐标是(0,0),其他部分在第三象限,
这个正方形不在坐标轴上的顶点的坐标是(﹣2,﹣2).
故选:B.
8.在第二象限内,到x轴距离为3,到y轴距离为2的点P坐标为( )
A.(3,2)
B.(2,3)
C.(﹣3,2)
D.(﹣2,3)
【分析】根据点到坐标轴的距离,可得x、y的值,再根据第二象限内点的横坐标小于零,纵坐标大于零,可得答案.
【解答】解:∵|x|=2,|y|=3,
∴x=±2,y=±3,
∵点P在第二象限,
∴P(﹣2,3),
故选:D.
二、填空题(共5小题,每小题3分,满分15分)
9.在y轴上,若点M与点N(0,3)的距离是6,则点M的坐标是 (0,﹣3)或(0,9) .
【分析】分点M在点N的上方与下方两种情况讨论求解即可.
【解答】解:①当点M在点N的上方时,3+6=9,
此时点M的坐标为(0,9),
②点M在点N的下方时,3﹣6=﹣3,
此时,点M的坐标为(0,﹣3),
综上所述,点M的坐标为(0,﹣3)或(0,9).
故答案为:(0,﹣3)或(0,9).
10.在x轴上,若点P与点Q(﹣2,0)的距离是5,则点P的坐标是 (﹣7,0)或(3,0) .
【分析】易得点P的纵坐标为0,横坐标为﹣2左边5个单位的数或﹣2右边5个单位的数,即可得解.
【解答】解:∵点P在x轴上,
∴点P的纵坐标为0,
∵点P与点Q(﹣2,0)的距离是5,
∴点P的横坐标为﹣2﹣5=﹣7或﹣2+5=3,
∴点P的坐标是(﹣7,0)或(3,0).
故答案填:(﹣7,0)或(3,0).
11.平面上有一点P(a,b),点P到x轴、y轴的距离分别为3、4,且ab<0,则点P的坐标是 (﹣4,3)或(4,﹣3) .
【分析】根据异号得负判断出x、y异号,再根据点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值求解即可.
【解答】解:∵ab<0,
∴a、b异号,
∵点P到x轴、y轴的距离分别为3、4,
∴x=﹣4,y=3或x=4,y=﹣3,
∴点P的坐标为(﹣4,3)或(4,﹣3).
故答案为:(﹣4,3)或(4,﹣3).
12.点P(m+3,m+1)在直角坐标系的x轴上,则P点坐标为 (2,0) .
【分析】根据x轴上点的坐标特点解答即可.
【解答】解:∵点P(m+3,m+1)在直角坐标系的x轴上,
∴这点的纵坐标是0,
∴m+1=0,解得,m=﹣1,
∴横坐标m+3=2,则点P的坐标是(2,0).
13.若点M(a﹣3,a+4)在y轴上,则M点的坐标为 (0,7) .
【分析】根据y轴上点的横坐标为0列方程求出a的值,然后求解即可.
【解答】解:∵点M(a﹣3,a+4)在y轴上,
∴a﹣3=0,
解得:a=3,
所以,a+4=7,
所以,点M的坐标为(0,7).
故答案为(0,7).
三、解答题(共1小题,满分0分)
14.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点P到x轴、y轴的距离相等;
(4)点Q的坐标为(1,5),直线PQ∥y轴.
【分析】(1)利用x轴上点的坐标性质纵坐标为0,进而得出a的值,即可得出答案;
(2)利用y轴上点的坐标性质横坐标为0,进而得出a的值,即可得出答案;
(3)利用点P到x轴、y轴的距离相等,得出横纵坐标相等或互为相反数进而得出答案;
(4)利用平行于y轴直线的性质,横坐标相等,进而得出a的值,进而得出答案.
【解答】解:(1)∵点P(a﹣2,2a+8)在x轴上,
∴2a+8=0,
解得:a=﹣4,
故a﹣2=﹣4﹣2=﹣6,
则P(﹣6,0);
(2)∵点P(a﹣2,2a+8)在y轴上,
∴a﹣2=0,
解得:a=2,
故2a+8=2×2+8=12,
则P(0,12);
(3)∵点P到x轴、y轴的距离相等,
∴a﹣2=2a+8或a﹣2+2a+8=0,
解得:a1=﹣10,a2=﹣2,
故当a=﹣10则:a﹣2=﹣12,2a+8=﹣12,
则P(﹣12,﹣12);
故当a=﹣2则:a﹣2=﹣4,2a+8=4,
则P(﹣4,4).
综上所述:P(﹣12,﹣12),(﹣4,4);
(4)∵点Q的坐标为(1,5),直线PQ∥y轴,
∴a﹣2=1,
解得:a=3,
故2a+8=14,
则P(1,14).
3.3轴对称与坐标变化
一、单选题
1.点P(1,﹣2)关于x轴对称的点的坐标为(??
)
A.(1,2)
B.(1,﹣2)
C.(﹣1,2)
D.(﹣1,﹣2)
2.在平面直角坐标系中,点P(-20,a)与点Q(b,13)关于x轴对称,则的值为(???)
A.7
B.-7
C.33
D.-33
3.点M(2,-3)关于原点对称的点N的坐标是:
( )
A.(-2,-3)
B.(-2, 3)
C.(2, 3)
D.(-3,
2)
4.已知M(a,3)和N(4,b)关于y轴对称,则的值为(????)
A.1
B.-1
C.
D.
5.已知点P?(3,
?2),点Q(?3,
2),点R(?3,
?2),点H(3,
2),下面选项中关于y轴对称的是(???
).
A.P和Q
B.P和H
C.Q和R
D.P和R
6.点P(-4,3)先向左平移2个单位,再向下平移2个单位,得点P?的坐标是(???)
A.(-2,5)
B.(-6,1)
C.(-6,5)
D.(-2,1)
7.在直角坐标系中,A(1,2)点的横坐标乘-1,纵坐标不变,得到A′点,则A与A′的关系是()
A.关于x轴对称
B.关于y轴对
C.关于原点对称
D.将A点向x轴负方向平移一个单位
8.点关于轴的对称点的坐标是,则点关于轴的对称点的坐标是(?)
A.
B.
C.
D.
9.如图,点A,B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则的值为()
A.2
B.3
C.4
D.5
10.在平面直角坐标系中,有、两点,则A与B关于(???)
A.x轴对称
B.y轴对称
C.原点对称
D.直线对称
二、填空题
11.在平面内,若点与点关于轴对称,则点的坐标为_____.
12.在平面直角坐标系中,点P(2,3)关于y轴对称的点的坐标是_____.
13.已知、关于x轴对称,、关于y轴对称,?(-3,4),则?的坐标为___________.
14.已知点M(2a-b,2b),点N(5,a)关于y轴对称,则a+b=___________
15.若过点的直线与轴平行,则点关于轴的对称点的坐标是_________.
16.若点A(a,b)和点B(3,﹣7)关于x轴对称,则a+b的值是__________.
三、解答题
17.如图,在平面直角坐标系中,?的三个顶点分别为,,?.
(1)请在图中作出?关于?轴的轴对称图形?(??、?、?的对称点分别是?、?、?),并直接写出?、?、?的坐标.
(2)求?的面积.
18.如图,三个顶点的坐标分别为,,.
(1)请画出关于轴成轴对称的图形,并写出、、的坐标;
(2)在轴上找一点,使的值最小,请画出点的位置.
19.如图,在平面直角坐标系中有一个轴对称图形,A(3,-2),B(3,﹣6)两点在此图形上且互为对称点,若此图形上有一个点C(﹣2,+1).
(1)求点C的对称点的坐标.
(2)求△ABC的面积.
20.如图,在正方形网格中。三角形ABC各顶点都在网格上,点A,C的坐标分别是(-5,1),(-1,4),结合给出的平面直角坐标系解答下列问题;
(1)画出关于y轴对称的;
(2)写出的坐标;
(3)求的面积;
第三章能力测试题含答案3.1确定位置
一、选择题(共10小题,3
10=30)
1.海事救灾船前去救援某海域失火轮船需要确定(
)
A.方位
B.距离
C.方位和距离
D.失火轮船的国籍
2.北京时间某年5月24日4时49分云南省德宏傣族景颇族自治州盈江县(北纬25.0°,东经97.8°)发生5.6级地震,能够准确表述这个地点位置的是(
)
A.北纬25.0°
B.东经97.8°
C.云南西部
D.北纬25.0°,东经97.8°
3.到电影院看电影需要对号入座,那么“对号入座”的意思是(
)
A.在电影院里随便找个座位坐下即可
B.在电影院里只要找到座位号即可
C.在电影院里只要找到排号即可
D.在电影院里既要找到排号,又要找到座位号
4.小强向同学们介绍图书馆的位置时,其中表达准确的是(
)
A.在学校的右边
B.距学校1
000米
C.在学校的西边
D.在学校的西边距学校1
000米处
5.老师对班上的同学的座位进行调整,下面说法能找到座位的是(
)
A.3排4列
B.从前数第3排4列
C.3排从左数第4列
D.从前数第3排,从左数第4列
6.
若我军战舰攻打敌军战舰,需要知道(
)
A.我军战舰的位置
B.敌军战舰相对于我军战舰的方向
C.敌军战舰相对于我军战舰的距离
D.敌军战舰相对于我军战舰的方向和距离
7.钓鱼岛历来就是中国不可分割的领土,中国对钓鱼岛及其附近海域拥有无可争辩的主权,能够准确表示钓鱼岛位置的是( )
A.北纬25°40′~26°
B.东经123°~124°34′
C.福建的正东方向
D.东经123°~124°34′,北纬25°40′~26°
8.七年级(2)班有45人参加学校运动会的入场仪式,队伍共有9排5列.如果用(2,4)表示第2排从左至右第4列的同学,那么第4排从左至右第6列的同学表示为( )
A.(4,10)
B.(4,6)
C.(10,6)
D.(6,4)
9.如图,有两种关于A,B两地位置关系的描述:
①B在A北偏东70°方向,与A相距100
m;
②A在B南偏西70°方向,与B相距100
m.
下列判断正确的是( )
A.①对②错
B.①对②对
C.①错②对
D.①错②错
10.如图是沈阳地区简图的一部分,图中“故宫”“鼓楼”所在的区域分别是( )
A.D7,E6
B.D6,E7
C.E7,D6
D.E6,D7
二.填空题(共8小题,3
8=24)
11.有人在市中心打听第一中学的位置,问了三个人,得到三种不同的回答:①在市中心的西北方向;②距市中心1
km;③在市中心的西北方向,距市中心1
km处.在上述回答中能确定第一中学位置的是__________.(填序号)
12.
课间操时,小华、小军、小刚的位置如图,小华的位置用(0,0)表示,小军的位置用(2,1)表示,那么小刚的位置可以表示成________.
13.如图是在方格纸上画出的小旗图案,若用(0,0)表示点A,(0,4)表示点B,那么点C的位置可表示为________.
14.如图所示,某班教室有9排5列座位.1号同学说:“小明在我的右后方.”2号同学说:“小明在我的左后方.”3号同学说:“小明在我的左前方.”4号同学说:“小明离1号同学和3号同学的距离一样远.”根据上面4位同学的描述,可知“5号”小明的位置在________.
15.如果电影票上的“5排2号”记作(5,2),那么(4,3)表示____________.
16..如图是小明所在学校的示意图,学校大门位于从左数第5条纵向网格线与从下数第1条横向网格线的交点上,它的位置表示为(5,1),则实验楼的位置表示为
___________,____的位置表示为(7,5).
17.如图,已知A(-2,1),B(-6,0),若白棋A飞挂后,黑棋C尖顶,黑棋C可以表示为(______,______).
18.如图,雷达探测器测得六个目标点A,B,C,D,E,F出现,按照规定的目标表示方法,目标点C,F的位置表示为C(6,120°),F(5,210°),按照此方法在表示目标点A,B,D的位置是_______________________________________.
三.解答题(共7小题,
46分)
19.(6分)
如图,某港口有一灯塔A,灯塔A的正东方向有一个小岛B,从灯塔A处看到在它的北偏东50°方向上有一艘轮船C.
(1)要确定轮船C的位置还需要哪些数据?
(2)从轮船C看灯塔A用怎样的方位角来表示?
20.(6分)
如图所示的“马”的位置为(2,3).
(1)你能表示图中“象”的位置吗?
(2)写出“马”下一步可以到达的位置.
21.(6分)
如图,小王家在2街与2大道的十字路口,如果用(2,2)→(2,3)→(2,4)→(3,4)→(4,4)→(5,4)表示小王从家到工厂上班的一条路径,那么你能用同样的方式写出由家到工厂小王走的另一条路径吗?
22.(6分)
如图,点A表示2街与4大道的十字路口,记为(2,4);点B表示4街与2大道的十字路口,记为(4,2).例如,可以用(2,4)→(2,3)→(3,3)→(4,3)→(4,2)表示从点A到点B的路径.
(1)请你用同样的方法写出其他两种表示从点A到点B的路径:
①__________________________________________________;
②__________________________________________________.
(2)请探究:从点A到点B的最短路径共有__________条.
23.(6分)
如图,请设计一条由学校到博物馆的路线,并分别用“××区(例如A3区)”表示这条路线所经过的区域.
24.(8分)
一次,小红在寄给小伙伴的信中附加了一张自己学校周边环境的示意图来介绍自己学校的位置及情况(如图),对于学校来说,
(1)正东方向上有哪些设施?要明确这些设施相对于学校的位置,还需要知道哪些数据?
(2)离学校最近的设施是什么?在学校的哪个方向上?这一方向上还有其他设施吗?怎样区分?
(3)要确定电视塔相对于学校的位置,需要知道哪些数据?
25.(8分)
如图,一只甲虫在10×10的方格(每个小方格的边长为1)纸上沿着网格线运动,它从C处出发想去看望A,B,D,E处的其他甲虫,规定:向下向左走为正,向上向右走为负.则从C到B记为C→B(+5,+2)(第一个数表示左、右方向,第二个数表示上、下方向).
(1)填空:C→D(____,____);C→A(____,____);D→____(+5,-6);E→____(____,-4).
(2)若这只甲虫的行走路线是C→A→B→D→E,请计算该甲虫走过的路程.
(3)这只甲虫从C处出发去另一只甲虫家P处的行走路线依次为(-2,+2),(+3,-4),(-4,+2),(+7,+3),请在图上描出这只甲虫的行走路线并标出P点的位置,想一想,有没有简便的方法?
参考答案
1-5CDDDD
6-10DDBBC
11.
③
12.
(4,3)
13.
(3,2)
14.
5排4列
15.
3排4号
16.
(3,7),操场
-1,1
18.
(5,30°)
,(2,90°),(4,240°)
19.
解:(1)点C到点A的距离
(2)灯塔A在轮船C的南偏西50°方向上
20.
解:(1)“象”的位置为(5,3)
(2)“马”的下一步可以到达的位置为(1,1),(3,1),(4,2),(1,5),(3,5),(4,4)
21.
解:小王从家到工厂上班的另一条路径可为:(2,2)→(3,2)→(4,2)→(5,2)→(5,3)→(5,4).
22.
解:(1)
(答案不唯一)(2,4)→(2,3)→(2,2)→(3,2)→(4,2)
(2,4)→(3,4)→(4,4)→(4,3)→(4,2)
(2)6
23.
解:路线:A4区→A3区→A2区→B2区→C2区→C1区→D1区→D2区.(答案不唯一)
24.
解:(1)正东方向上有超市和艺术中心,要明确这些设施相对于学校的位置,还需要知道它们与学校的距离.
(2)离学校最近的设施是儿童公园,它在学校南偏西30°的方向上;这一方向上还有农贸市场;它们与学校的距离不同.
(3)要确定电视塔相对于学校的位置,需要知道它的方位角和距离.
25.
解:(1)+2,+4,+7,-2,A,D,+5
(2)7+2+2+4+3+2+5+4=29.
(3)如图,简便方法:所行走路线的第一个数与第二个数分别相加,所得结果即为C到P的行走路线,即C→P(+4,+3).
3.2
平面直角坐标系
一、选择题(共8小题,每小题3分,满分24分)
1.已知点P位于x轴上方,距离x轴4个单位长度,位于y轴右侧,距y轴3个单位长度,则点P坐标是( )
A.(﹣3,4)
B.(﹣4,3)
C.(3,4)
D.(4,3)
2.已知在直角坐标系中有点P(x、y),且x、y满足条件|x|=5,|x﹣y|=8,则这样的点P有( )
A.1个
B.2个
C.4个
D.8个
3.第二象限内一点P到x轴的距离等于2,到y轴的距离等于3,则点P的坐标为( )
A.(﹣2,3)
B.(2,﹣3)
C.(﹣3,2)
D.(3,﹣2)
4.已知点P到x轴的距离为1,到y轴的距离为2,则点P的坐标不可能为( )
A.(1,2)
B.(﹣2,﹣1)
C.(2,﹣1)
D.(2,1)
5.在平面直角坐标系中,点(﹣5,2)所在的象限为( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.如果点P(m+3,m+1)在x轴上,则点P的坐标为( )
A.(0,2)
B.(2,0)
C.(4,0)
D.(0,﹣4)
7.正方形的两条边在坐标轴上,其中一个顶点的坐标是(0,0),其他部分在第三象限,面积为4,那么这个正方形不在坐标轴上的顶点的坐标是( )
A.(2,2)
B.(﹣2,﹣2)
C.(﹣2,2)
D.(2,﹣2)
8.在第二象限内,到x轴距离为3,到y轴距离为2的点P坐标为( )
A.(3,2)
B.(2,3)
C.(﹣3,2)
D.(﹣2,3)
二、填空题(共5小题,每小题3分,满分15分)
9.在y轴上,若点M与点N(0,3)的距离是6,则点M的坐标是
.
10.在x轴上,若点P与点Q(﹣2,0)的距离是5,则点P的坐标是
.
11.平面上有一点P(a,b),点P到x轴、y轴的距离分别为3、4,且ab<0,则点P的坐标是
.
12.点P(m+3,m+1)在直角坐标系的x轴上,则P点坐标为
.
13.若点M(a﹣3,a+4)在y轴上,则M点的坐标为
.
三、解答题(共1小题,满分0分)
14.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点P到x轴、y轴的距离相等;
(4)点Q的坐标为(1,5),直线PQ∥y轴.
参考答案与试题解析
一、选择题(共8小题,每小题3分,满分24分)
1.已知点P位于x轴上方,距离x轴4个单位长度,位于y轴右侧,距y轴3个单位长度,则点P坐标是( )
A.(﹣3,4)
B.(﹣4,3)
C.(3,4)
D.(4,3)
【分析】根据题意,P点应在第一象限,横、纵坐标为正,再根据P点到坐标轴的距离确定点的坐标.
【解答】解:∵P点位于y轴右侧,x轴上方,
∴P点在第一象限,
又∵P点距y轴3个单位长度,距x轴4个单位长度,
∴P点横坐标为3,纵坐标为4,即点P的坐标为(3,4).
故选:C.
2.已知在直角坐标系中有点P(x、y),且x、y满足条件|x|=5,|x﹣y|=8,则这样的点P有( )
A.1个
B.2个
C.4个
D.8个
【分析】根据题意,由|x|=5可得,x=±5,又由|x﹣y|=8,即x﹣y=±8,代入x的值,解可得y的值,进而可得解的组数,即可得答案.
【解答】解:根据题意,
由|x|=5可得,x=±5,
又由|x﹣y|=8,即x﹣y=±8,
当x=5时,可得y=13或﹣3,
当x=﹣5时,可得y=﹣13或3,
即这样的点P有4个,分别为(5,﹣3),(5,13),(﹣5,3),(﹣5,﹣13);
故选:C.
3.第二象限内一点P到x轴的距离等于2,到y轴的距离等于3,则点P的坐标为( )
A.(﹣2,3)
B.(2,﹣3)
C.(﹣3,2)
D.(3,﹣2)
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值解答即可.
【解答】解:∵第二象限内一点P到x轴的距离等于2,到y轴的距离等于3,
∴点P的横坐标为﹣3,纵坐标为2,
∴点P的坐标为(﹣3,2).
故选:C.
4.已知点P到x轴的距离为1,到y轴的距离为2,则点P的坐标不可能为( )
A.(1,2)
B.(﹣2,﹣1)
C.(2,﹣1)
D.(2,1)
【分析】根据点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度求出点P可能的横坐标与纵坐标,即可得解.
【解答】解:∵点P到x轴的距离为1,到y轴的距离为2,
∴点P的横坐标为2或﹣2,纵坐标为1或﹣1,
∴点P的坐标不可能为(1,2).
故选:A.
5.在平面直角坐标系中,点(﹣5,2)所在的象限为( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
【分析】根据各象限内点的坐标特征解答即可.
【解答】解:点(﹣5,2)在第二象限.
故选:B.
6.如果点P(m+3,m+1)在x轴上,则点P的坐标为( )
A.(0,2)
B.(2,0)
C.(4,0)
D.(0,﹣4)
【分析】根据点P在x轴上,即y=0,可得出m的值,从而得出点P的坐标.
【解答】解:∵点P(m+3,m+1)在x轴上,
∴y=0,
∴m+1=0,
解得:m=﹣1,
∴m+3=﹣1+3=2,
∴点P的坐标为(2,0).
故选:B.
7.正方形的两条边在坐标轴上,其中一个顶点的坐标是(0,0),其他部分在第三象限,面积为4,那么这个正方形不在坐标轴上的顶点的坐标是( )
A.(2,2)
B.(﹣2,﹣2)
C.(﹣2,2)
D.(2,﹣2)
【分析】根据正方形的性质即可得这个正方形不在坐标轴上的顶点的坐标.
【解答】解:因为正方形的面积为4,
所以正方形的边长为2,
因为正方形的两条边在坐标轴上,其中一个顶点的坐标是(0,0),其他部分在第三象限,
这个正方形不在坐标轴上的顶点的坐标是(﹣2,﹣2).
故选:B.
8.在第二象限内,到x轴距离为3,到y轴距离为2的点P坐标为( )
A.(3,2)
B.(2,3)
C.(﹣3,2)
D.(﹣2,3)
【分析】根据点到坐标轴的距离,可得x、y的值,再根据第二象限内点的横坐标小于零,纵坐标大于零,可得答案.
【解答】解:∵|x|=2,|y|=3,
∴x=±2,y=±3,
∵点P在第二象限,
∴P(﹣2,3),
故选:D.
二、填空题(共5小题,每小题3分,满分15分)
9.在y轴上,若点M与点N(0,3)的距离是6,则点M的坐标是 (0,﹣3)或(0,9) .
【分析】分点M在点N的上方与下方两种情况讨论求解即可.
【解答】解:①当点M在点N的上方时,3+6=9,
此时点M的坐标为(0,9),
②点M在点N的下方时,3﹣6=﹣3,
此时,点M的坐标为(0,﹣3),
综上所述,点M的坐标为(0,﹣3)或(0,9).
故答案为:(0,﹣3)或(0,9).
10.在x轴上,若点P与点Q(﹣2,0)的距离是5,则点P的坐标是 (﹣7,0)或(3,0) .
【分析】易得点P的纵坐标为0,横坐标为﹣2左边5个单位的数或﹣2右边5个单位的数,即可得解.
【解答】解:∵点P在x轴上,
∴点P的纵坐标为0,
∵点P与点Q(﹣2,0)的距离是5,
∴点P的横坐标为﹣2﹣5=﹣7或﹣2+5=3,
∴点P的坐标是(﹣7,0)或(3,0).
故答案填:(﹣7,0)或(3,0).
11.平面上有一点P(a,b),点P到x轴、y轴的距离分别为3、4,且ab<0,则点P的坐标是 (﹣4,3)或(4,﹣3) .
【分析】根据异号得负判断出x、y异号,再根据点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值求解即可.
【解答】解:∵ab<0,
∴a、b异号,
∵点P到x轴、y轴的距离分别为3、4,
∴x=﹣4,y=3或x=4,y=﹣3,
∴点P的坐标为(﹣4,3)或(4,﹣3).
故答案为:(﹣4,3)或(4,﹣3).
12.点P(m+3,m+1)在直角坐标系的x轴上,则P点坐标为 (2,0) .
【分析】根据x轴上点的坐标特点解答即可.
【解答】解:∵点P(m+3,m+1)在直角坐标系的x轴上,
∴这点的纵坐标是0,
∴m+1=0,解得,m=﹣1,
∴横坐标m+3=2,则点P的坐标是(2,0).
13.若点M(a﹣3,a+4)在y轴上,则M点的坐标为 (0,7) .
【分析】根据y轴上点的横坐标为0列方程求出a的值,然后求解即可.
【解答】解:∵点M(a﹣3,a+4)在y轴上,
∴a﹣3=0,
解得:a=3,
所以,a+4=7,
所以,点M的坐标为(0,7).
故答案为(0,7).
三、解答题(共1小题,满分0分)
14.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点P到x轴、y轴的距离相等;
(4)点Q的坐标为(1,5),直线PQ∥y轴.
【分析】(1)利用x轴上点的坐标性质纵坐标为0,进而得出a的值,即可得出答案;
(2)利用y轴上点的坐标性质横坐标为0,进而得出a的值,即可得出答案;
(3)利用点P到x轴、y轴的距离相等,得出横纵坐标相等或互为相反数进而得出答案;
(4)利用平行于y轴直线的性质,横坐标相等,进而得出a的值,进而得出答案.
【解答】解:(1)∵点P(a﹣2,2a+8)在x轴上,
∴2a+8=0,
解得:a=﹣4,
故a﹣2=﹣4﹣2=﹣6,
则P(﹣6,0);
(2)∵点P(a﹣2,2a+8)在y轴上,
∴a﹣2=0,
解得:a=2,
故2a+8=2×2+8=12,
则P(0,12);
(3)∵点P到x轴、y轴的距离相等,
∴a﹣2=2a+8或a﹣2+2a+8=0,
解得:a1=﹣10,a2=﹣2,
故当a=﹣10则:a﹣2=﹣12,2a+8=﹣12,
则P(﹣12,﹣12);
故当a=﹣2则:a﹣2=﹣4,2a+8=4,
则P(﹣4,4).
综上所述:P(﹣12,﹣12),(﹣4,4);
(4)∵点Q的坐标为(1,5),直线PQ∥y轴,
∴a﹣2=1,
解得:a=3,
故2a+8=14,
则P(1,14).
3.3轴对称与坐标变化
一、单选题
1.点P(1,﹣2)关于x轴对称的点的坐标为(??
)
A.(1,2)
B.(1,﹣2)
C.(﹣1,2)
D.(﹣1,﹣2)
2.在平面直角坐标系中,点P(-20,a)与点Q(b,13)关于x轴对称,则的值为(???)
A.7
B.-7
C.33
D.-33
3.点M(2,-3)关于原点对称的点N的坐标是:
( )
A.(-2,-3)
B.(-2, 3)
C.(2, 3)
D.(-3,
2)
4.已知M(a,3)和N(4,b)关于y轴对称,则的值为(????)
A.1
B.-1
C.
D.
5.已知点P?(3,
?2),点Q(?3,
2),点R(?3,
?2),点H(3,
2),下面选项中关于y轴对称的是(???
).
A.P和Q
B.P和H
C.Q和R
D.P和R
6.点P(-4,3)先向左平移2个单位,再向下平移2个单位,得点P?的坐标是(???)
A.(-2,5)
B.(-6,1)
C.(-6,5)
D.(-2,1)
7.在直角坐标系中,A(1,2)点的横坐标乘-1,纵坐标不变,得到A′点,则A与A′的关系是()
A.关于x轴对称
B.关于y轴对
C.关于原点对称
D.将A点向x轴负方向平移一个单位
8.点关于轴的对称点的坐标是,则点关于轴的对称点的坐标是(?)
A.
B.
C.
D.
9.如图,点A,B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则的值为()
A.2
B.3
C.4
D.5
10.在平面直角坐标系中,有、两点,则A与B关于(???)
A.x轴对称
B.y轴对称
C.原点对称
D.直线对称
二、填空题
11.在平面内,若点与点关于轴对称,则点的坐标为_____.
12.在平面直角坐标系中,点P(2,3)关于y轴对称的点的坐标是_____.
13.已知、关于x轴对称,、关于y轴对称,?(-3,4),则?的坐标为___________.
14.已知点M(2a-b,2b),点N(5,a)关于y轴对称,则a+b=___________
15.若过点的直线与轴平行,则点关于轴的对称点的坐标是_________.
16.若点A(a,b)和点B(3,﹣7)关于x轴对称,则a+b的值是__________.
三、解答题
17.如图,在平面直角坐标系中,?的三个顶点分别为,,?.
(1)请在图中作出?关于?轴的轴对称图形?(??、?、?的对称点分别是?、?、?),并直接写出?、?、?的坐标.
(2)求?的面积.
18.如图,三个顶点的坐标分别为,,.
(1)请画出关于轴成轴对称的图形,并写出、、的坐标;
(2)在轴上找一点,使的值最小,请画出点的位置.
19.如图,在平面直角坐标系中有一个轴对称图形,A(3,-2),B(3,﹣6)两点在此图形上且互为对称点,若此图形上有一个点C(﹣2,+1).
(1)求点C的对称点的坐标.
(2)求△ABC的面积.
20.如图,在正方形网格中。三角形ABC各顶点都在网格上,点A,C的坐标分别是(-5,1),(-1,4),结合给出的平面直角坐标系解答下列问题;
(1)画出关于y轴对称的;
(2)写出的坐标;
(3)求的面积;
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
