华东师大版九年级上册数学 专题训练(六):24.3 求锐角三角函数方法归类(Word版 含答案)
文档属性
| 名称 | 华东师大版九年级上册数学 专题训练(六):24.3 求锐角三角函数方法归类(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 98.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 00:00:00 | ||
图片预览


文档简介
专题训练(六) 求锐角三角函数方法归类
如图,直线y=x+3与x轴、y轴分别交于A,B两点,则sin∠BAO的值是(
)
A.
B.
C.
D.
在Rt△ABC中,∠C=90°,tanA=,则sinA=(
)
A.
B.
C.
D.
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD∶CD=3∶2,则tanB=(
)
A.
B.
C.
D.
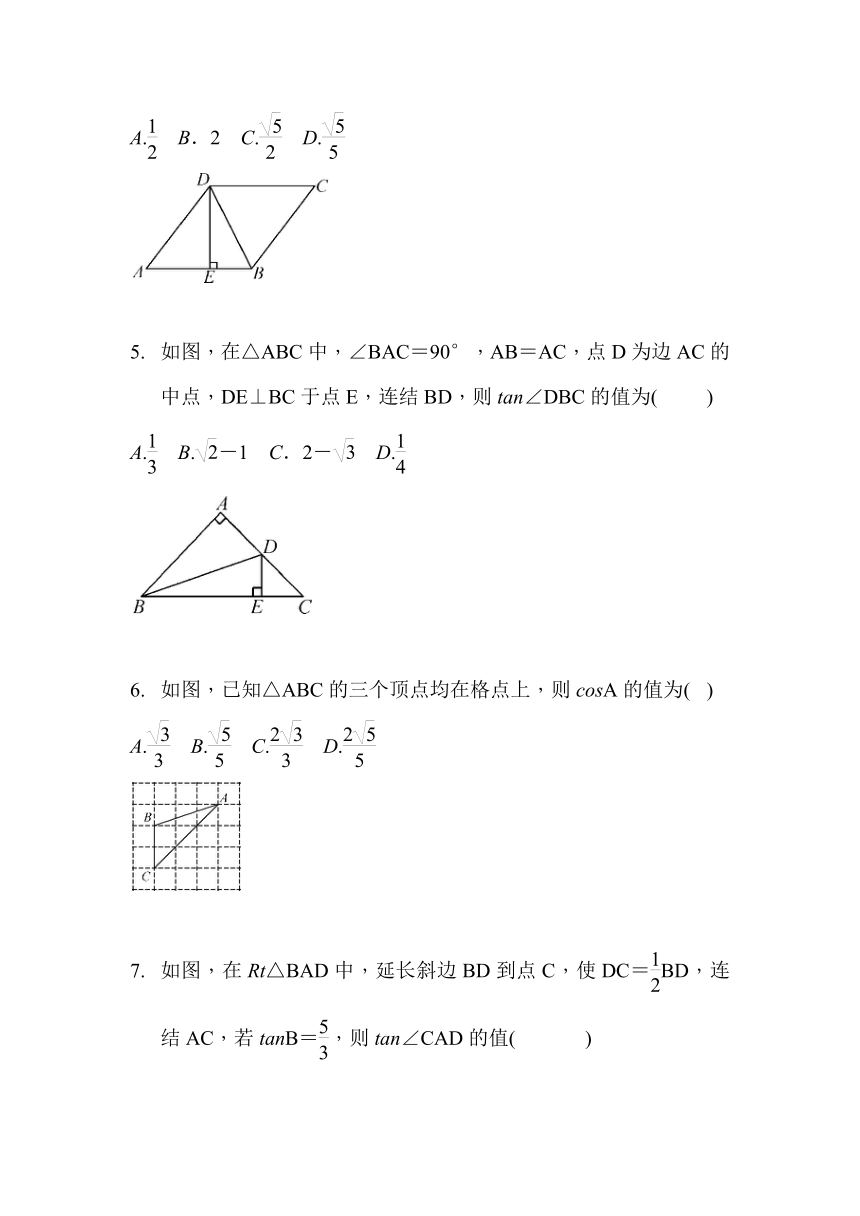
如图,在菱形ABCD中,DE⊥AB,cosA=,BE=2,则tan∠DBE的值为(
)
A.
B.2
C.
D.
如图,在△ABC中,∠BAC=90°,AB=AC,点D为边AC的中点,DE⊥BC于点E,连结BD,则tan∠DBC的值为(
)
A.
B.-1
C.2-
D.
如图,已知△ABC的三个顶点均在格点上,则cosA的值为(
)
A.
B.
C.
D.
如图,在Rt△BAD中,延长斜边BD到点C,使DC=BD,连结AC,若tanB=,则tan∠CAD的值(
)
A.
B.
C.
D.
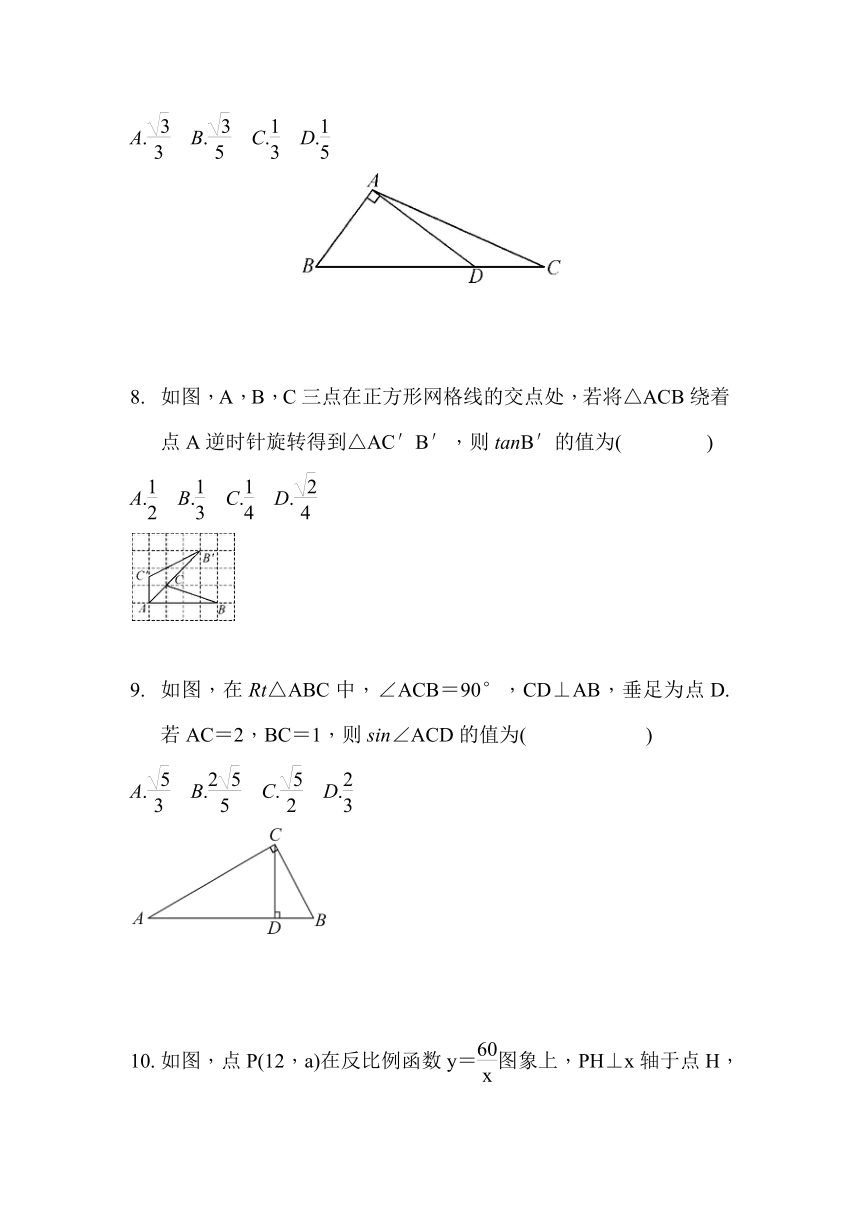
如图,A,B,C三点在正方形网格线的交点处,若将△ACB绕着点A逆时针旋转得到△AC′B′,则tanB′的值为(
)
A.
B.
C.
D.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D.若AC=2,BC=1,则sin∠ACD的值为(
)
A.
B.
C.
D.
如图,点P(12,a)在反比例函数y=图象上,PH⊥x轴于点H,则tan∠POH的值为
.
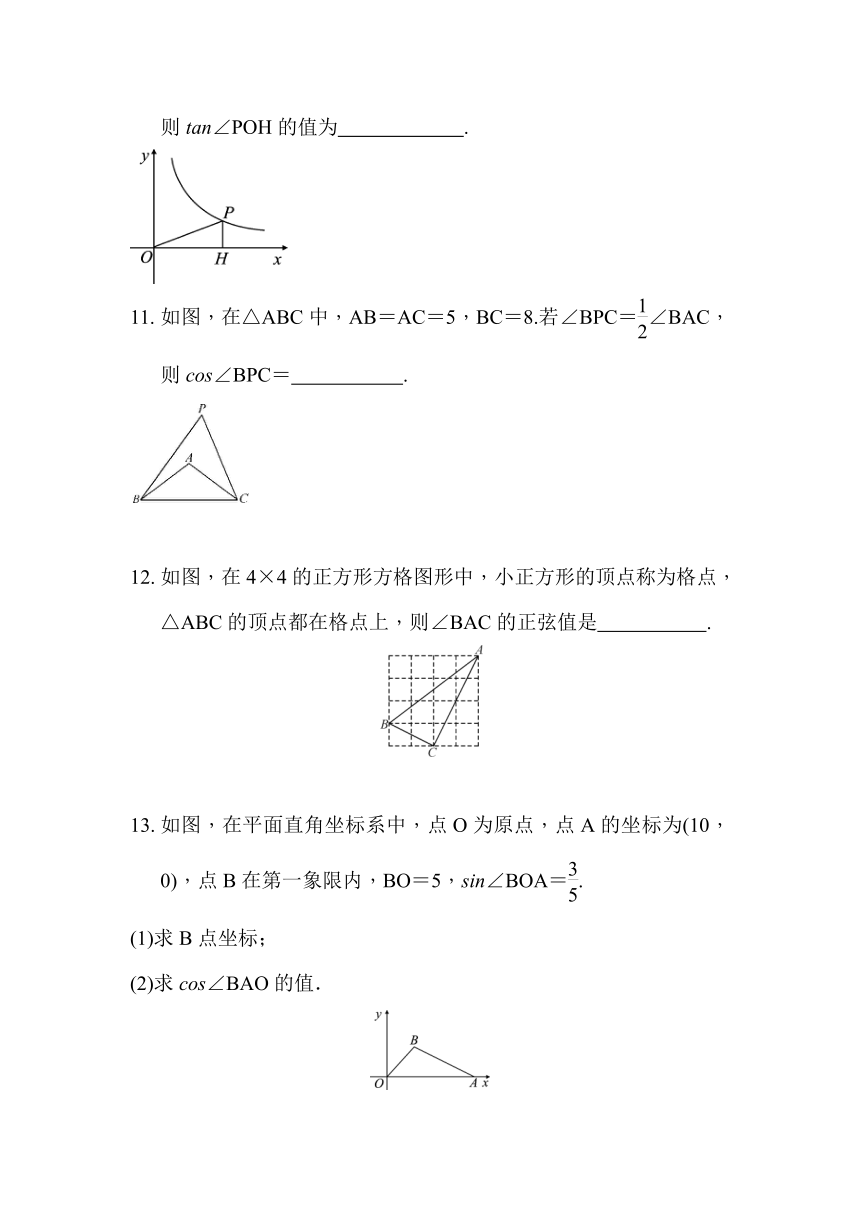
如图,在△ABC中,AB=AC=5,BC=8.若∠BPC=∠BAC,则cos∠BPC=
.
如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则∠BAC的正弦值是
.
如图,在平面直角坐标系中,点O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.
(1)求B点坐标;
(2)求cos∠BAO的值.
如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=,AD=1.求:
(1)BC的长;
(2)tan∠DAE的值.
如图,在正方形ABCD中,点M是AD的中点,BE=3AE,求cos∠ECM的值.
如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).
(1)求证:△ACE≌△AFE;
(2)求tan∠CAE的值.
如图,AD是△ABC的中线,tanB=,cosC=,AC=.求:
(1)BC的长;
(2)sin∠ADC的值.
若想求tan15°的值,如图,可先画Rt△ABC,使∠C=90°,∠BAC=30°,再延长CA到点D,使DA=AB,连结BD,你能求出tan15°的值吗?请你试一试.
答案:
1.
B
2.
A
3.
D
4.
B
5.
A
6.
D
7.
D
8.
B
9.
B
10.
11.
12.
13.
解:(1)B(4,3)
(2)cos∠BAO=
14.
解:(1)AD是BC边上的高,∴∠ADB=∠ADC=90°.∵∠ADC=90°,∠C=45°,AD=1,∴DC=AD=1.在△ADB中,∠ADB=90°,sinB=,AD=1,∴AB==3,∴BD==2,∴BC=BD+DC=2+1
(2)∵AE是BC边上的中线,∴CE=BC=+,∴DE=CE-CD=-,∴tan∠DAE==-
15.
解:设AB=BC=CD=AD=4k,则AE=k,BE=3k,AM=DM=2k,由勾股定理得EM2=AE2+AM2=5k2,CM2=CD2+MD2=20k2,CE2=BC2+BE2=25k2,∴CE2=EM2+CM2,CM=2k,CE=5k,∴∠EMC=90°,∴cos∠ECM===
16.
解:(1)∵AE是∠BAC的平分线,EC⊥AC,FE⊥AF,∴CE=EF.在Rt△ACE与Rt△AFE中,∴Rt△ACE≌Rt△AFE(HL)
(2)由(1)可知△ACE≌△AFE,∴AC=AF,CE=EF.设BF=m,则AC=2m,AF=2m,AB=3m,∴BC===m,∴在Rt△ABC中,tanB===.在Rt△EFB中,EF=BF·tanB=,∴CE=EF=.在Rt△ACE中,tan∠CAE===,∴tan∠CAE=
17.
解:(1)过点A作AE⊥BC于点E,∵cosC=,∴∠C=45°,在Rt△ACE中,CE=AC·cosC=1,∴AE=CE=1,在Rt△ABE中,tanB=,即=,∴BE=3AE=3,∴BC=BE+CE=4
(2)∵AD是△ABC的中线,∴CD=BC=2,∴DE=CD-CE=1,∵AE⊥BC,DE=AE,∴∠ADC=45°,∴sin∠ADC=
18.
解:∵AD=AB,∴∠D=∠ABD,∵∠D+∠ABD=30°,∴∠D=15°.在Rt△ABC中,∠BAC=30°,设BC=k(k>0),则AB=2k,AC=k,∴AD=2k,∴tanD===2-,即tan15°=2-
如图,直线y=x+3与x轴、y轴分别交于A,B两点,则sin∠BAO的值是(
)
A.
B.
C.
D.
在Rt△ABC中,∠C=90°,tanA=,则sinA=(
)
A.
B.
C.
D.
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD∶CD=3∶2,则tanB=(
)
A.
B.
C.
D.
如图,在菱形ABCD中,DE⊥AB,cosA=,BE=2,则tan∠DBE的值为(
)
A.
B.2
C.
D.
如图,在△ABC中,∠BAC=90°,AB=AC,点D为边AC的中点,DE⊥BC于点E,连结BD,则tan∠DBC的值为(
)
A.
B.-1
C.2-
D.
如图,已知△ABC的三个顶点均在格点上,则cosA的值为(
)
A.
B.
C.
D.
如图,在Rt△BAD中,延长斜边BD到点C,使DC=BD,连结AC,若tanB=,则tan∠CAD的值(
)
A.
B.
C.
D.
如图,A,B,C三点在正方形网格线的交点处,若将△ACB绕着点A逆时针旋转得到△AC′B′,则tanB′的值为(
)
A.
B.
C.
D.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为点D.若AC=2,BC=1,则sin∠ACD的值为(
)
A.
B.
C.
D.
如图,点P(12,a)在反比例函数y=图象上,PH⊥x轴于点H,则tan∠POH的值为
.
如图,在△ABC中,AB=AC=5,BC=8.若∠BPC=∠BAC,则cos∠BPC=
.
如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则∠BAC的正弦值是
.
如图,在平面直角坐标系中,点O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=.
(1)求B点坐标;
(2)求cos∠BAO的值.
如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=,AD=1.求:
(1)BC的长;
(2)tan∠DAE的值.
如图,在正方形ABCD中,点M是AD的中点,BE=3AE,求cos∠ECM的值.
如图,在Rt△ABC中,∠C=90°,∠BAC的平分线交BC于点E,EF⊥AB于点F,点F恰好是AB的一个三等分点(AF>BF).
(1)求证:△ACE≌△AFE;
(2)求tan∠CAE的值.
如图,AD是△ABC的中线,tanB=,cosC=,AC=.求:
(1)BC的长;
(2)sin∠ADC的值.
若想求tan15°的值,如图,可先画Rt△ABC,使∠C=90°,∠BAC=30°,再延长CA到点D,使DA=AB,连结BD,你能求出tan15°的值吗?请你试一试.
答案:
1.
B
2.
A
3.
D
4.
B
5.
A
6.
D
7.
D
8.
B
9.
B
10.
11.
12.
13.
解:(1)B(4,3)
(2)cos∠BAO=
14.
解:(1)AD是BC边上的高,∴∠ADB=∠ADC=90°.∵∠ADC=90°,∠C=45°,AD=1,∴DC=AD=1.在△ADB中,∠ADB=90°,sinB=,AD=1,∴AB==3,∴BD==2,∴BC=BD+DC=2+1
(2)∵AE是BC边上的中线,∴CE=BC=+,∴DE=CE-CD=-,∴tan∠DAE==-
15.
解:设AB=BC=CD=AD=4k,则AE=k,BE=3k,AM=DM=2k,由勾股定理得EM2=AE2+AM2=5k2,CM2=CD2+MD2=20k2,CE2=BC2+BE2=25k2,∴CE2=EM2+CM2,CM=2k,CE=5k,∴∠EMC=90°,∴cos∠ECM===
16.
解:(1)∵AE是∠BAC的平分线,EC⊥AC,FE⊥AF,∴CE=EF.在Rt△ACE与Rt△AFE中,∴Rt△ACE≌Rt△AFE(HL)
(2)由(1)可知△ACE≌△AFE,∴AC=AF,CE=EF.设BF=m,则AC=2m,AF=2m,AB=3m,∴BC===m,∴在Rt△ABC中,tanB===.在Rt△EFB中,EF=BF·tanB=,∴CE=EF=.在Rt△ACE中,tan∠CAE===,∴tan∠CAE=
17.
解:(1)过点A作AE⊥BC于点E,∵cosC=,∴∠C=45°,在Rt△ACE中,CE=AC·cosC=1,∴AE=CE=1,在Rt△ABE中,tanB=,即=,∴BE=3AE=3,∴BC=BE+CE=4
(2)∵AD是△ABC的中线,∴CD=BC=2,∴DE=CD-CE=1,∵AE⊥BC,DE=AE,∴∠ADC=45°,∴sin∠ADC=
18.
解:∵AD=AB,∴∠D=∠ABD,∵∠D+∠ABD=30°,∴∠D=15°.在Rt△ABC中,∠BAC=30°,设BC=k(k>0),则AB=2k,AC=k,∴AD=2k,∴tanD===2-,即tan15°=2-
