人教版数学八年级上册14.2.1平方差公式 课件(16张)
文档属性
| 名称 | 人教版数学八年级上册14.2.1平方差公式 课件(16张) |  | |
| 格式 | zip | ||
| 文件大小 | 551.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 19:20:32 | ||
图片预览






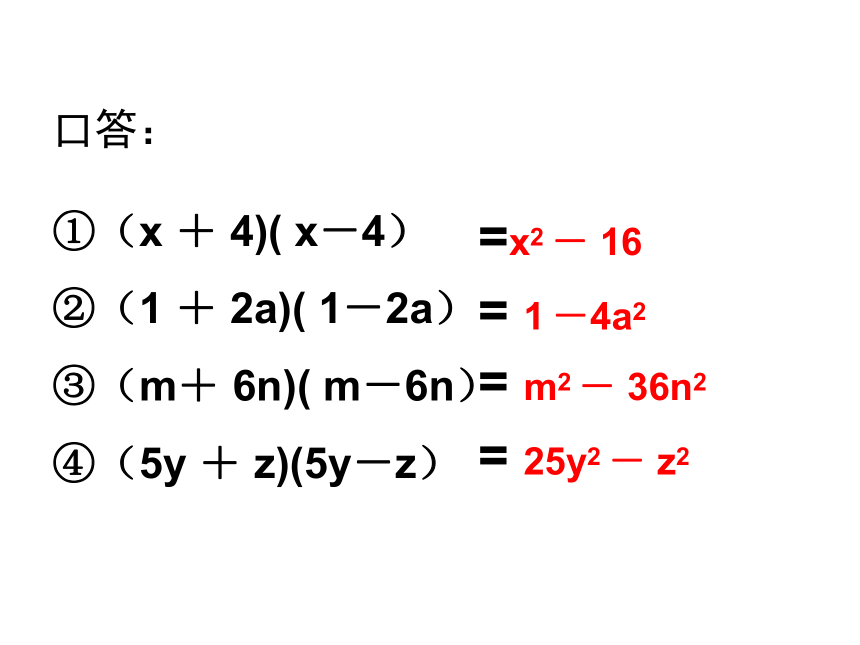
文档简介
(共16张PPT)
14.2.1
平方差公式
计算:
(x+1)(x-1)
=
(m+2)(m-2)
=
(2x+1)(2x-1)
=
x2
-
1
m2
-
4
4x2
-
1
猜想:
(a+b)(a-b)
=
规律探索:
(a+b)(a-b)
=
a2-b2
验证:
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,
等于这两个数的平方差。
平方差公式
文字叙述:
字母表示:
(a+b)(a-b)=a2-b2
公式结构特征:
1、等号左边是两个
相乘,且这两
个
中有一项
,另一
项
。
2、等号右边是
的平方减去
的
平方。
二项式
二项式
完全相同
符号相反
相同项
相反项
下列各式中,能用平方差公式运算的是(
)
A.(-a+b)(-a-b)
B.(a-b)(b-a)
C.(2a-3b)(3a+2b)
D.(-a+c)(a-c)
2.下列各式中,不能用平方差公式计算的是(
)
A.(x-2y)(2y+x)
B.(-x+2y)(-x-2y)
C.(-2y-x)(x+2y)
D.(-2b-5)(2b-5)
A
C
选择:
口答:
①(x
+
4)(
x-4)
②(1
+
2a)(
1-2a)
③(m+
6n)(
m-6n)
④(5y
+
z)(5y-z)
=x2
-
16
=
1
-4a2
=
m2
-
36n2
=
25y2
-
z2
运用平方差公式计算:
1、(m+n)(-n+m)
=
2、(-x-y)
(x-y)
=
3、(2a+b)(2a-b)
=
4、(x2+y2)(x2-y2)=
m2-n2
位置变化
y2-x2
符号变化
4a2-b2
系数变化
x4-y4
指数变化
速算
21
×
19
54
×
46
88
×
92
102×
98
计算:
(2X
-
y)(-y
-
2X
)
(ab-
c)(ab
+
c
)
(-4k+
mn)(-4k
-
mn
)
104×96
(a+b)(a-b)=a2-b2
有两个完全相同的项
和两个符号相反的项
平方差公式
特征:
字母:
小结
简记:
两项之和×两项之差
=
相同项平方-相反项平方
a、b可以是数,也可以是整式
注意:
知识延伸
灵活运用平方差公式计算:
(1)(3x+4)(3x-4)
–
(2x+3)(3x-2);
(2)(x+y)(x-y)(x2+y2);
注意:
运用公式前,首先要判断两个多项式能否变形为公式的标准形式。
5米
5米
a米
(a-5)
(a+5)米
相等吗?
原来
现在
面积变了吗?
a2
(a+5)(a-5)
(3x+2)(3x-2)
(-x+2y)(-x-2y)
例1
知识应用
例2
(y+2)(y-2)-(y+5)(y-1)
102×98
谢
谢
14.2.1
平方差公式
计算:
(x+1)(x-1)
=
(m+2)(m-2)
=
(2x+1)(2x-1)
=
x2
-
1
m2
-
4
4x2
-
1
猜想:
(a+b)(a-b)
=
规律探索:
(a+b)(a-b)
=
a2-b2
验证:
(a+b)(a-b)=a2-b2
两个数的和与这两个数的差的积,
等于这两个数的平方差。
平方差公式
文字叙述:
字母表示:
(a+b)(a-b)=a2-b2
公式结构特征:
1、等号左边是两个
相乘,且这两
个
中有一项
,另一
项
。
2、等号右边是
的平方减去
的
平方。
二项式
二项式
完全相同
符号相反
相同项
相反项
下列各式中,能用平方差公式运算的是(
)
A.(-a+b)(-a-b)
B.(a-b)(b-a)
C.(2a-3b)(3a+2b)
D.(-a+c)(a-c)
2.下列各式中,不能用平方差公式计算的是(
)
A.(x-2y)(2y+x)
B.(-x+2y)(-x-2y)
C.(-2y-x)(x+2y)
D.(-2b-5)(2b-5)
A
C
选择:
口答:
①(x
+
4)(
x-4)
②(1
+
2a)(
1-2a)
③(m+
6n)(
m-6n)
④(5y
+
z)(5y-z)
=x2
-
16
=
1
-4a2
=
m2
-
36n2
=
25y2
-
z2
运用平方差公式计算:
1、(m+n)(-n+m)
=
2、(-x-y)
(x-y)
=
3、(2a+b)(2a-b)
=
4、(x2+y2)(x2-y2)=
m2-n2
位置变化
y2-x2
符号变化
4a2-b2
系数变化
x4-y4
指数变化
速算
21
×
19
54
×
46
88
×
92
102×
98
计算:
(2X
-
y)(-y
-
2X
)
(ab-
c)(ab
+
c
)
(-4k+
mn)(-4k
-
mn
)
104×96
(a+b)(a-b)=a2-b2
有两个完全相同的项
和两个符号相反的项
平方差公式
特征:
字母:
小结
简记:
两项之和×两项之差
=
相同项平方-相反项平方
a、b可以是数,也可以是整式
注意:
知识延伸
灵活运用平方差公式计算:
(1)(3x+4)(3x-4)
–
(2x+3)(3x-2);
(2)(x+y)(x-y)(x2+y2);
注意:
运用公式前,首先要判断两个多项式能否变形为公式的标准形式。
5米
5米
a米
(a-5)
(a+5)米
相等吗?
原来
现在
面积变了吗?
a2
(a+5)(a-5)
(3x+2)(3x-2)
(-x+2y)(-x-2y)
例1
知识应用
例2
(y+2)(y-2)-(y+5)(y-1)
102×98
谢
谢
