人教版数学七年级上册3.1.2用等式的性质解方程课件(26张)
文档属性
| 名称 | 人教版数学七年级上册3.1.2用等式的性质解方程课件(26张) |  | |
| 格式 | zip | ||
| 文件大小 | 484.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 19:21:26 | ||
图片预览


文档简介
(共26张PPT)
3.1.2
等式的性质
像这样用等号“=”表示相等关系的式子叫等式
知识
准备
什么是等式?
a
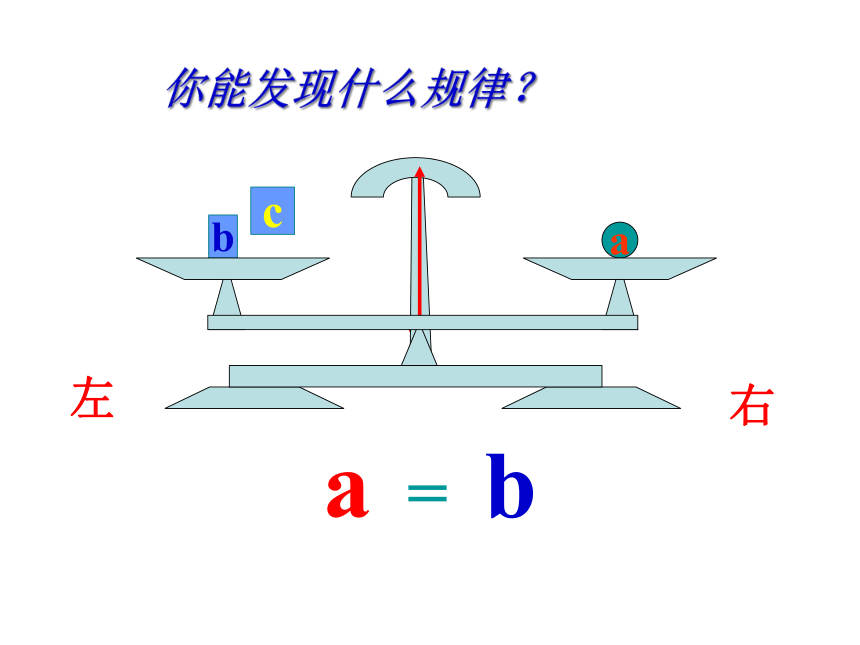
你能发现什么规律?
右
左
a
你能发现什么规律?
右
左
a
b
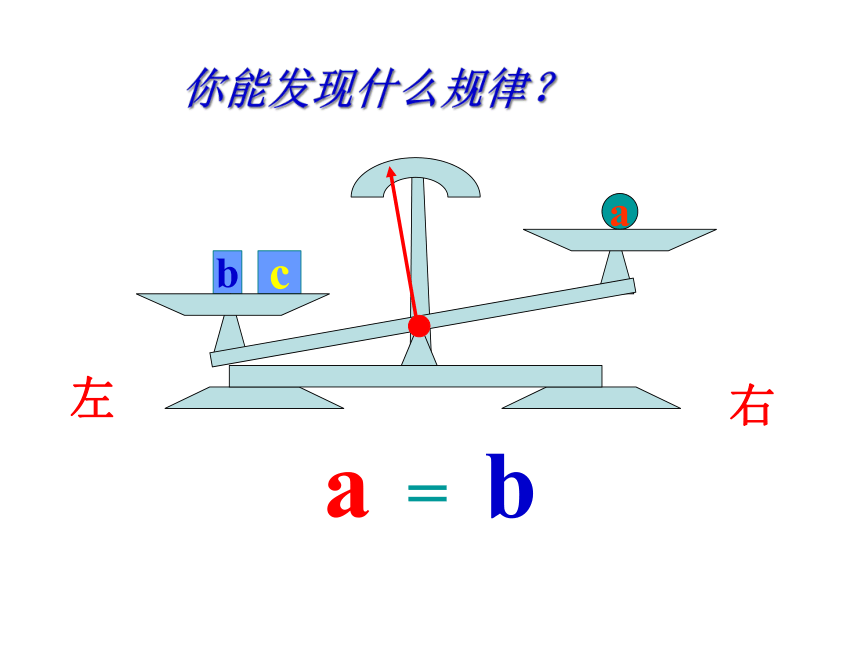
你能发现什么规律?
右
左
b
a
你能发现什么规律?
a
=
b
右
左
b
a
你能发现什么规律?
a
=
b
c
右
左
a
c
b
你能发现什么规律?
a
=
b
右
左
c
b
c
a
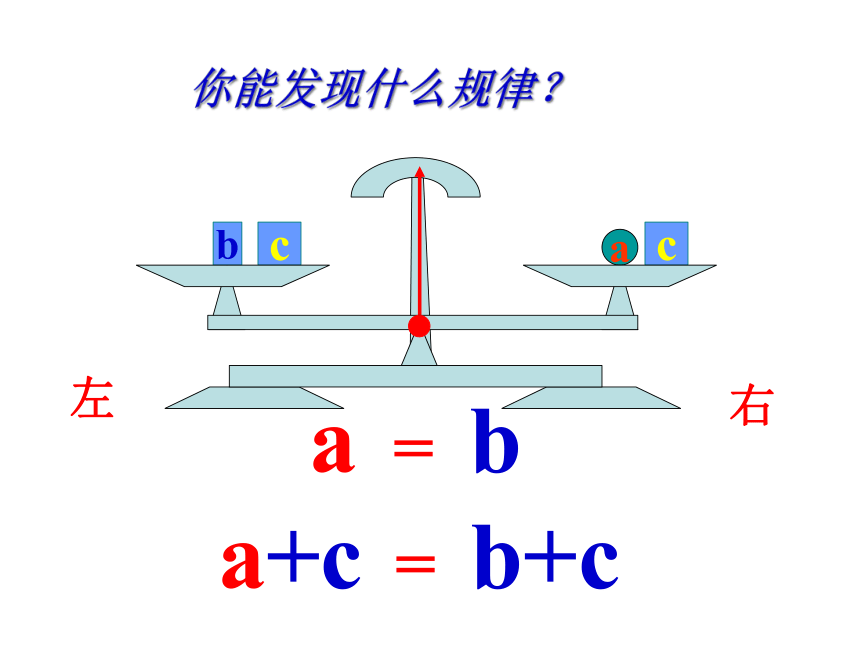
你能发现什么规律?
a
=
b
a+c
b+c
=
右
左
c
c
你能发现什么规律?
a
=
b
a
b
右
左
c
你能发现什么规律?
a
=
b
a
b
右
左
你能发现什么规律?
a
=
b
a-c
b-c
=
b
a
右
左
归纳
等式的性质1:
等式两边同加(或同减)同一个数(或式子),结果仍相等。
如果a=b,那么a+c=b+c
b
a
你能发现什么规律?
a
=
b
右
左
b
a
你能发现什么规律?
a
=
b
右
左
a
b
2a
=
2b
b
a
你能发现什么规律?
a
=
b
右
左
b
b
a
a
3a
=
3b
b
a
你能发现什么规律?
a
=
b
右
左
b
b
b
b
b
b
a
a
a
a
a
a
C个
C个
ac
=
bc
b
a
你能发现什么规律?
a
=
b
右
左
等式的性质2:
等式两边都乘以同一个数,或都除以同一个不为0的数,结果仍相等。
如果a=b,那么ac=bc;
如果a=b(c
≠
0),那么
归纳
在下面的括号内填上适当的数或者代数式:
想一想
2
1)由
可得
2)由
可得
(1)如果3x+4=7
,
那么3x=________,
其依据是
________
,在等式的两边都________.
(2)如果
-
2x=
8
,
那么x=________,其依据是
________
,在等式的两边都________.
(3)如果
–x
=
3,
那么
x
=________
(4)
如果
-
2x
=
4,
那么x
=________。
(5)
如果2x-
,
那么6x-1=________.
3
等式的性质1
-2
-3
-4
等式的性质2
除以-2
减去4
2
填一填:
1、填依据:在下列各题的括号内,填上使等式成立的依据.
(1)
得
(
)
(2)
得
(
)
(3)
得
(
)
(4)
得
(
)
(5)
得
(
)
(6)
得
(
)
(7)
得
(
)
等式的性质2
等式的性质1
等式的性质2
等式的性质1
等式的性质2
等式的性质1
等式的性质2
例2:利用等式的性质解下列方程:
(1)x
+
7
=
26;
(2)-
5
x
=
20;
(3)-
-
x
–
5
=
4.
3
1
解以x为未知数的方程,就是把方程逐步转化为x=a(常数)的形式,等式的性质是转化的重要依据。
怎样检验?
练习:利用等式的性质解下列方程并检验
(P83页)
(1)x
-
5
=
6;
(2)0.3
x
=
45;
(3)5
x
+4=
0;
(3)2
–
-
x
=
3.
4
1
x
=
11
x
=
150
x
=
-
4
本节课你学到了什么?
课堂小结
(1)等式的性质。
(2)等式性质的应用。
等式性质1:等式两边加(或减)同一个数(或式
子),结果仍相等。
等式性质2:等式的两边乘同一个数,或除以同
一个不为0的数,所的结果仍相等。
记住了
?
作业
课本P83、84页
第
3、4、9、10、11题
3.1.2
等式的性质
像这样用等号“=”表示相等关系的式子叫等式
知识
准备
什么是等式?
a
你能发现什么规律?
右
左
a
你能发现什么规律?
右
左
a
b
你能发现什么规律?
右
左
b
a
你能发现什么规律?
a
=
b
右
左
b
a
你能发现什么规律?
a
=
b
c
右
左
a
c
b
你能发现什么规律?
a
=
b
右
左
c
b
c
a
你能发现什么规律?
a
=
b
a+c
b+c
=
右
左
c
c
你能发现什么规律?
a
=
b
a
b
右
左
c
你能发现什么规律?
a
=
b
a
b
右
左
你能发现什么规律?
a
=
b
a-c
b-c
=
b
a
右
左
归纳
等式的性质1:
等式两边同加(或同减)同一个数(或式子),结果仍相等。
如果a=b,那么a+c=b+c
b
a
你能发现什么规律?
a
=
b
右
左
b
a
你能发现什么规律?
a
=
b
右
左
a
b
2a
=
2b
b
a
你能发现什么规律?
a
=
b
右
左
b
b
a
a
3a
=
3b
b
a
你能发现什么规律?
a
=
b
右
左
b
b
b
b
b
b
a
a
a
a
a
a
C个
C个
ac
=
bc
b
a
你能发现什么规律?
a
=
b
右
左
等式的性质2:
等式两边都乘以同一个数,或都除以同一个不为0的数,结果仍相等。
如果a=b,那么ac=bc;
如果a=b(c
≠
0),那么
归纳
在下面的括号内填上适当的数或者代数式:
想一想
2
1)由
可得
2)由
可得
(1)如果3x+4=7
,
那么3x=________,
其依据是
________
,在等式的两边都________.
(2)如果
-
2x=
8
,
那么x=________,其依据是
________
,在等式的两边都________.
(3)如果
–x
=
3,
那么
x
=________
(4)
如果
-
2x
=
4,
那么x
=________。
(5)
如果2x-
,
那么6x-1=________.
3
等式的性质1
-2
-3
-4
等式的性质2
除以-2
减去4
2
填一填:
1、填依据:在下列各题的括号内,填上使等式成立的依据.
(1)
得
(
)
(2)
得
(
)
(3)
得
(
)
(4)
得
(
)
(5)
得
(
)
(6)
得
(
)
(7)
得
(
)
等式的性质2
等式的性质1
等式的性质2
等式的性质1
等式的性质2
等式的性质1
等式的性质2
例2:利用等式的性质解下列方程:
(1)x
+
7
=
26;
(2)-
5
x
=
20;
(3)-
-
x
–
5
=
4.
3
1
解以x为未知数的方程,就是把方程逐步转化为x=a(常数)的形式,等式的性质是转化的重要依据。
怎样检验?
练习:利用等式的性质解下列方程并检验
(P83页)
(1)x
-
5
=
6;
(2)0.3
x
=
45;
(3)5
x
+4=
0;
(3)2
–
-
x
=
3.
4
1
x
=
11
x
=
150
x
=
-
4
本节课你学到了什么?
课堂小结
(1)等式的性质。
(2)等式性质的应用。
等式性质1:等式两边加(或减)同一个数(或式
子),结果仍相等。
等式性质2:等式的两边乘同一个数,或除以同
一个不为0的数,所的结果仍相等。
记住了
?
作业
课本P83、84页
第
3、4、9、10、11题
