人教版九年级数学下册28.1-28.2基础过关测试题(Word版 含答案)
文档属性
| 名称 | 人教版九年级数学下册28.1-28.2基础过关测试题(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 340.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 19:53:40 | ||
图片预览




文档简介
人教版九年级数学下册28.1:--28.2基础过关测试题含答案
28.1锐角三角函数
一、选择题
1.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,如果a2+b2=c2,那么下列结论正确的是(
)
A.csinA=a
B.bcosB=c
C.atanA=b
D.ctanB=b
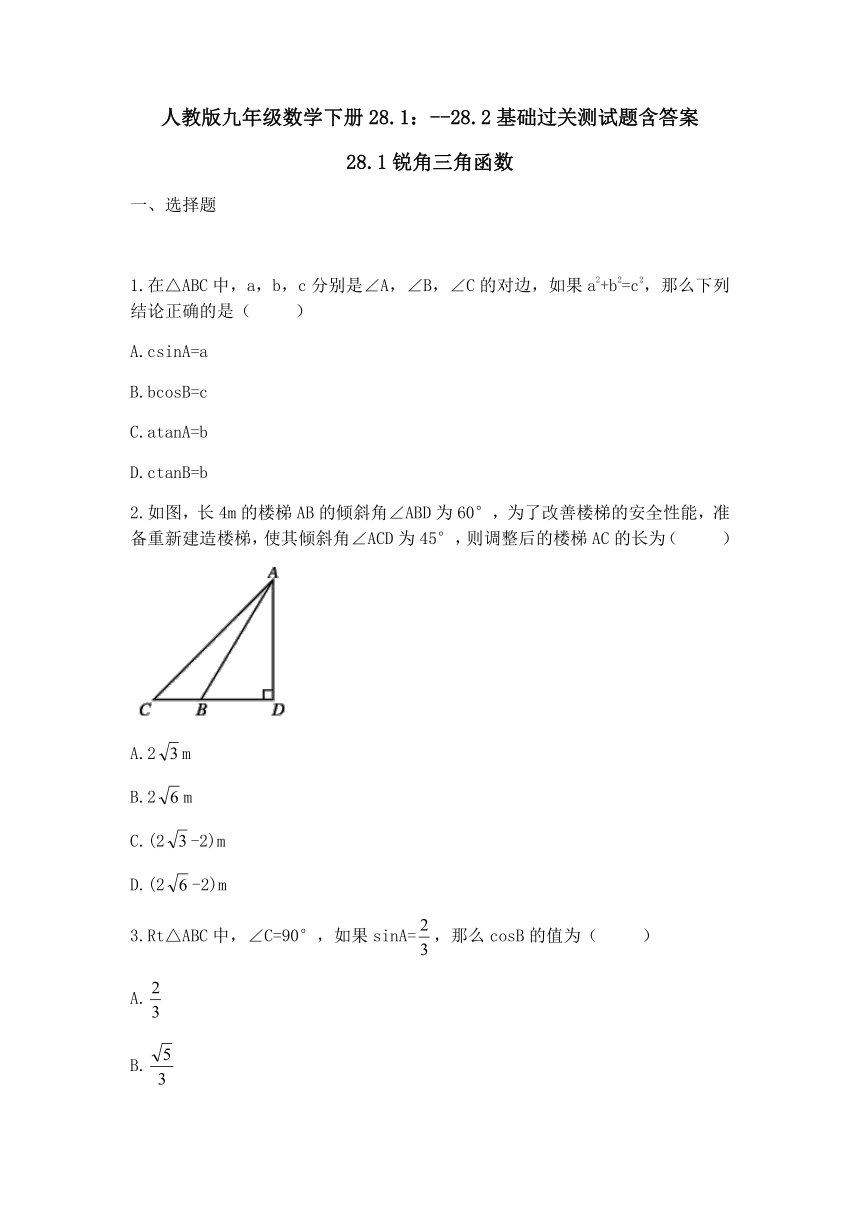
2.如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为(
)
A.2m
B.2m
C.(2-2)m
D.(2-2)m
3.Rt△ABC中,∠C=90°,如果sinA=,那么cosB的值为(
)
A.
B.
C.
D.不能确定
4.式子2cos30°-tan45°-的值是(
)
A.2-2
B.0
C.2
D.2
5.2sin60°的值等于(
)
A.1
B.2
C.3
D.2
6.为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)i=1:2.4的山坡AB上发现有一棵古树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为(
)
(参考数据:sin
48°≈0.73,cos8°≈0.67,tan48°≈1.11)
?
A.17.0米
???
B.21.9米
???
C.23.3米
???
D.33.3米
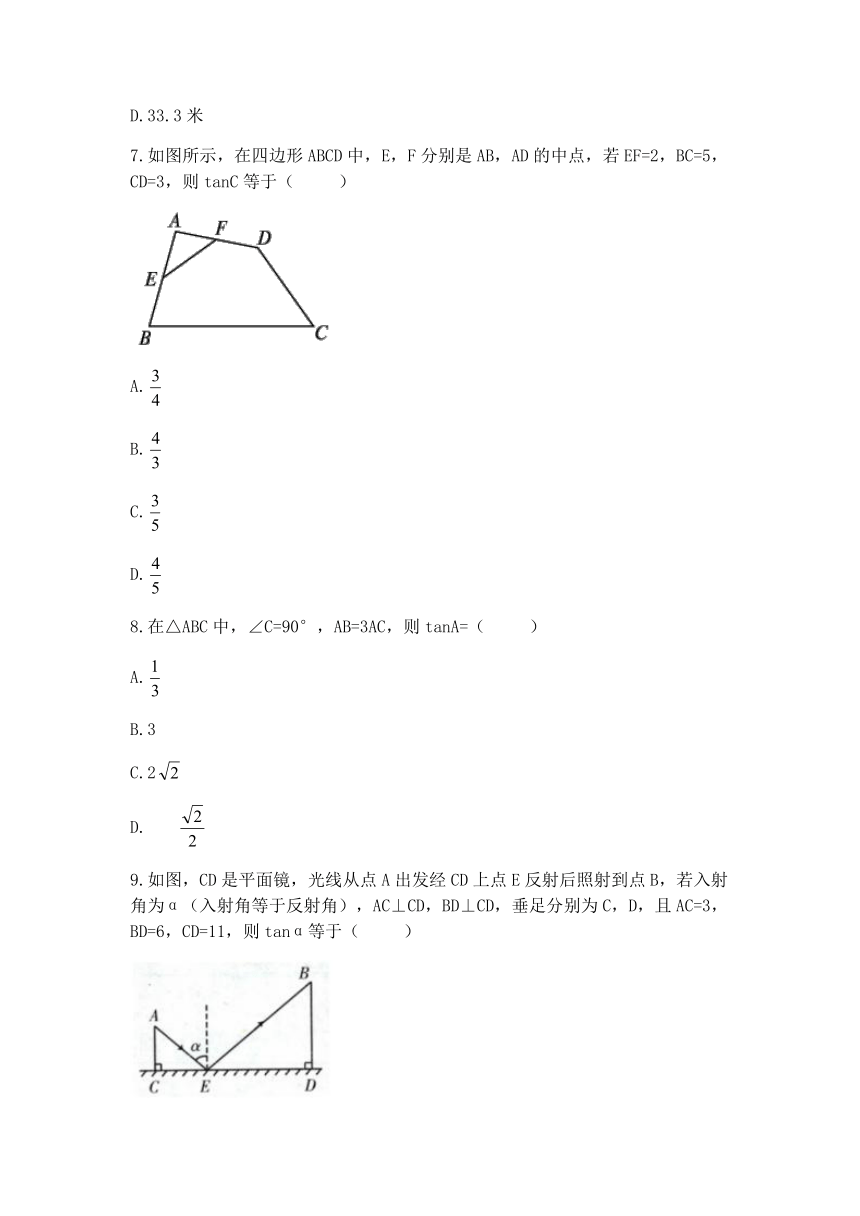
7.如图所示,在四边形ABCD中,E,F分别是AB,AD的中点,若EF=2,BC=5,CD=3,则tanC等于(
)
A.
B.
C.
D.
8.在△ABC中,∠C=90°,AB=3AC,则tanA=(
)
A.
B.3
C.2
D.
9.如图,CD是平面镜,光线从点A出发经CD上点E反射后照射到点B,若入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=6,CD=11,则tanα等于(
)
A.
B.
C.
D.
10.如图,在半径为6cm的⊙O中,点A是劣弧的中点,点D是优弧BC上一点,且∠D=30°.下列四个结论:①OA⊥BC;②BC=6cm;③sin∠AOB=;④四边形ABOC是菱形.其中正确结论的序号是(
)
A.①③
?
?
?
?
?
B.①②③④
?
?
?
?
C.②③④
?
?
?
?
D.①③④
二、填空题
11.计算:(π-3.14)0+2cos60°=???
。
12.cos60°的值
??
.
13.如图,在Rt△ABC中,∠C=90°,我们把锐角A的????与????的比叫做锐角A的正弦,记作???
,即sinA==???
.
14.如图,AB是⊙O的直径,=,AB=5,BD=4,则sin∠ECB=???
.
15.如图,在四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB=,则cos∠ADC=???
.
16.已知锐角三角函数值也可求相应的锐角,按键顺序为:先按???
键,再按键或键或键,然后输入???
,最后按键就可求出相应角度.
17.已知tanα=,则锐角α=???
;若cosα-=0,则锐角α=???
.
18.若∠A是锐角,且tanA=,则cosA=????.
三、解答题
19.如图,在△ABC中,AB=AC=6,BC=4,求sinB的值.
20.如图,在Rt△ABC中,已知AC=5,BC=3,求sinA和sinB的值.
21.已知a,b,c是△ABC的三边长,且a,b,c满足b2=(c+a)(c-a).若5b-4c=0,sinA+sinB的值.
22.研究锐角α的正弦、余弦与正切值之间的关系.
???
比较同一个锐角的sinαcosaα与tanα的值,由比较的结果你能得出什么猜想?
(2)试用计算器计算,并将结果直接填入表格中.(结果精确到0.0001)
?
比较表中的数值,你能验证你的猜想吗?
(3)请利用直角三角形来验证你的猜想.
23.已知α是锐角,cos(α-15°)=,求|cosα-tan|的值.
24.已知下列锐角三角函数值,用计算器求其相应的锐角(精确到1′):
(1)sinA=0.9532;
(2)cosA=0.8607;
(3)tanA=0.1890.
?
初中数学人教版九年级下册28.1锐角三角函数
1~10.ABABC,CBCDB
11.2
12.
13.对边,斜边,sinA,对边,.
14.
15.
16.,三角函数值.
17.60°;60°
18.
19.
20.
21.
22.
23.
24.
解:(1)∵sinA=0.9532,
∴∠A≈72.402°≈72°24′.
(2)∵cosA=0.8607,
∴∠A≈30.605°=30°36′.
(3)∵tanA=0.1890,
∴∠A≈10.703°≈10°42′.
28.2解直角三角形及其应用
一、选择题
直角梯形ABCD如图放置,AB、CD为水平线,,如果,从低处A处看高处C处,那么点C在点A的
A.
俯角方向
B.
俯角方向
C.
仰角方向
D.
仰角方向
如图,一个直角梯形的堤坝坡长AB为6米,斜坡AB的坡角为,为了改善堤坝的稳固性,准备将其坡角改为,则调整后的斜坡AE的长度为
A.
米
B.
米
C.
米
D.
米
如图,由四个全等的直角三角形围成的大正方形的面积是169,小正方形的面积为49,则
A.
B.
C.
D.
跳伞运动员小李在200米的空中测得地面上的着落点A的俯角为,那么此时小李离着落点A的距离是
A.
200米
B.
400米
C.
米
D.
米
如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为,若米,米,CE平行于江面AB,迎水坡BC的坡度:,坡长米,则此时AB的长约为参考数据:,,.
A.
米
B.
米
C.
米
D.
米
如图,中,,,于点E,D是线段BE上的一个动点,则的最小值是
A.
B.
C.
D.
10
有这样一道题:如图,在正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,连接DH,如果,,则的值为
A.
B.
C.
D.
如图是一斜坡的横截面,某人沿斜坡从M出发,走了13米到达N处,此时在铅垂方向上上升了5米,那么该斜坡的坡度是
A.
1:5
B.
12:13
C.
5:13
D.
5:12
如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是和,则该电线杆PQ的高度
A.
B.
C.
D.
如图中是抛物线形拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为,且,,以O为原点,OA所在直线为x轴建立直角坐标系,若水面上升1m,水面宽为??
.
A.
B.
C.
D.
二、填空题(本大题共10小题,共30.0分)
小明沿坡比为1:的山坡向上走了100米.那么他升高了______米.
如图,在中,,,,则AC的长为______.
如图,某校教学楼AC与实验楼BD的水平间距米,在实验楼顶部B点测得教学楼顶部A点的仰角是,底部C点的俯角是,则教学楼AC的高度是______米结果保留根号.
某兴趣小组借助无人飞机航拍,如图,无人飞机从A处飞行至B处需12秒,在地面C处同一方向上分别测得A处的仰角为,B处的仰角为已知无人飞机的飞行速度为3米秒,则这架无人飞机的飞行高度为结果保留根号______米.
已知中,,,,则的面积等于______.
在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于O,则的值等于______.
如图,从甲楼底部A处测得乙楼顶部C处的仰角是,从甲楼顶部B处测得乙楼底部D处的俯角是,已知甲楼的高AB是120m,则乙楼的高CD是______结果保留根号
如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据:米,米,,,则CD的长为______米.结果保留根号
一艘货轮以的速度在海面上沿正东方向航行,当行驶至A处时,发现它的东南方向有一灯塔B,货轮继续向东航行30分钟后到达C处,发现灯塔B在它的南偏东方向,则此时货轮与灯塔B的距离是______km.
如图,在菱形ABCD中,,点E,F分别在边AD、BC上,将四边形AEFB沿EF翻折,使AB的对应线段MN经过顶点C,当时,的值是______.
三、解答题
如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为沿坡面AB向上走到B处测得广告牌顶部C的仰角为,已知山坡AB的坡度:,米,米.:是指坡面的铅直高度BH与水平宽度AH的比
求点B距水平面AE的高度BH;
求广告牌CD的高度.
测角器的高度忽略不计,结果精确到米.参考数据:,
放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?风筝线AD,BD均为线段,?,?,最后结果精确到1米.
1.
D
2.
A
3.
D
4.
D
5.
A
6.
B
7.
D
8.
D
9.
A
10.
A
11.
50??
12.
2??
13.
??
14.
??
15.
或??
16.
??
17.
??
18.
??
19.
18??
20.
??
21.
解:过B作于G,
中,,
,
;
,,,
四边形BHEG是矩形.
由得:,,
,
中,,
.
中,,,
.
.
答:宣传牌CD高约米.??
22.
解:作于H,设米.
,
在直角中,,,,
在直角中,,,,
米,
,
,
小明此时所收回的风筝的长度为:
米.
答:小明此时所收回的风筝线的长度约是8米.??
28.1锐角三角函数
一、选择题
1.在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,如果a2+b2=c2,那么下列结论正确的是(
)
A.csinA=a
B.bcosB=c
C.atanA=b
D.ctanB=b
2.如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为(
)
A.2m
B.2m
C.(2-2)m
D.(2-2)m
3.Rt△ABC中,∠C=90°,如果sinA=,那么cosB的值为(
)
A.
B.
C.
D.不能确定
4.式子2cos30°-tan45°-的值是(
)
A.2-2
B.0
C.2
D.2
5.2sin60°的值等于(
)
A.1
B.2
C.3
D.2
6.为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)i=1:2.4的山坡AB上发现有一棵古树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为(
)
(参考数据:sin
48°≈0.73,cos8°≈0.67,tan48°≈1.11)
?
A.17.0米
???
B.21.9米
???
C.23.3米
???
D.33.3米
7.如图所示,在四边形ABCD中,E,F分别是AB,AD的中点,若EF=2,BC=5,CD=3,则tanC等于(
)
A.
B.
C.
D.
8.在△ABC中,∠C=90°,AB=3AC,则tanA=(
)
A.
B.3
C.2
D.
9.如图,CD是平面镜,光线从点A出发经CD上点E反射后照射到点B,若入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=6,CD=11,则tanα等于(
)
A.
B.
C.
D.
10.如图,在半径为6cm的⊙O中,点A是劣弧的中点,点D是优弧BC上一点,且∠D=30°.下列四个结论:①OA⊥BC;②BC=6cm;③sin∠AOB=;④四边形ABOC是菱形.其中正确结论的序号是(
)
A.①③
?
?
?
?
?
B.①②③④
?
?
?
?
C.②③④
?
?
?
?
D.①③④
二、填空题
11.计算:(π-3.14)0+2cos60°=???
。
12.cos60°的值
??
.
13.如图,在Rt△ABC中,∠C=90°,我们把锐角A的????与????的比叫做锐角A的正弦,记作???
,即sinA==???
.
14.如图,AB是⊙O的直径,=,AB=5,BD=4,则sin∠ECB=???
.
15.如图,在四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB=,则cos∠ADC=???
.
16.已知锐角三角函数值也可求相应的锐角,按键顺序为:先按???
键,再按键或键或键,然后输入???
,最后按键就可求出相应角度.
17.已知tanα=,则锐角α=???
;若cosα-=0,则锐角α=???
.
18.若∠A是锐角,且tanA=,则cosA=????.
三、解答题
19.如图,在△ABC中,AB=AC=6,BC=4,求sinB的值.
20.如图,在Rt△ABC中,已知AC=5,BC=3,求sinA和sinB的值.
21.已知a,b,c是△ABC的三边长,且a,b,c满足b2=(c+a)(c-a).若5b-4c=0,sinA+sinB的值.
22.研究锐角α的正弦、余弦与正切值之间的关系.
???
比较同一个锐角的sinαcosaα与tanα的值,由比较的结果你能得出什么猜想?
(2)试用计算器计算,并将结果直接填入表格中.(结果精确到0.0001)
?
比较表中的数值,你能验证你的猜想吗?
(3)请利用直角三角形来验证你的猜想.
23.已知α是锐角,cos(α-15°)=,求|cosα-tan|的值.
24.已知下列锐角三角函数值,用计算器求其相应的锐角(精确到1′):
(1)sinA=0.9532;
(2)cosA=0.8607;
(3)tanA=0.1890.
?
初中数学人教版九年级下册28.1锐角三角函数
1~10.ABABC,CBCDB
11.2
12.
13.对边,斜边,sinA,对边,.
14.
15.
16.,三角函数值.
17.60°;60°
18.
19.
20.
21.
22.
23.
24.
解:(1)∵sinA=0.9532,
∴∠A≈72.402°≈72°24′.
(2)∵cosA=0.8607,
∴∠A≈30.605°=30°36′.
(3)∵tanA=0.1890,
∴∠A≈10.703°≈10°42′.
28.2解直角三角形及其应用
一、选择题
直角梯形ABCD如图放置,AB、CD为水平线,,如果,从低处A处看高处C处,那么点C在点A的
A.
俯角方向
B.
俯角方向
C.
仰角方向
D.
仰角方向
如图,一个直角梯形的堤坝坡长AB为6米,斜坡AB的坡角为,为了改善堤坝的稳固性,准备将其坡角改为,则调整后的斜坡AE的长度为
A.
米
B.
米
C.
米
D.
米
如图,由四个全等的直角三角形围成的大正方形的面积是169,小正方形的面积为49,则
A.
B.
C.
D.
跳伞运动员小李在200米的空中测得地面上的着落点A的俯角为,那么此时小李离着落点A的距离是
A.
200米
B.
400米
C.
米
D.
米
如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为,若米,米,CE平行于江面AB,迎水坡BC的坡度:,坡长米,则此时AB的长约为参考数据:,,.
A.
米
B.
米
C.
米
D.
米
如图,中,,,于点E,D是线段BE上的一个动点,则的最小值是
A.
B.
C.
D.
10
有这样一道题:如图,在正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,连接DH,如果,,则的值为
A.
B.
C.
D.
如图是一斜坡的横截面,某人沿斜坡从M出发,走了13米到达N处,此时在铅垂方向上上升了5米,那么该斜坡的坡度是
A.
1:5
B.
12:13
C.
5:13
D.
5:12
如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是和,则该电线杆PQ的高度
A.
B.
C.
D.
如图中是抛物线形拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为,且,,以O为原点,OA所在直线为x轴建立直角坐标系,若水面上升1m,水面宽为??
.
A.
B.
C.
D.
二、填空题(本大题共10小题,共30.0分)
小明沿坡比为1:的山坡向上走了100米.那么他升高了______米.
如图,在中,,,,则AC的长为______.
如图,某校教学楼AC与实验楼BD的水平间距米,在实验楼顶部B点测得教学楼顶部A点的仰角是,底部C点的俯角是,则教学楼AC的高度是______米结果保留根号.
某兴趣小组借助无人飞机航拍,如图,无人飞机从A处飞行至B处需12秒,在地面C处同一方向上分别测得A处的仰角为,B处的仰角为已知无人飞机的飞行速度为3米秒,则这架无人飞机的飞行高度为结果保留根号______米.
已知中,,,,则的面积等于______.
在如图的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB与CD相交于O,则的值等于______.
如图,从甲楼底部A处测得乙楼顶部C处的仰角是,从甲楼顶部B处测得乙楼底部D处的俯角是,已知甲楼的高AB是120m,则乙楼的高CD是______结果保留根号
如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据:米,米,,,则CD的长为______米.结果保留根号
一艘货轮以的速度在海面上沿正东方向航行,当行驶至A处时,发现它的东南方向有一灯塔B,货轮继续向东航行30分钟后到达C处,发现灯塔B在它的南偏东方向,则此时货轮与灯塔B的距离是______km.
如图,在菱形ABCD中,,点E,F分别在边AD、BC上,将四边形AEFB沿EF翻折,使AB的对应线段MN经过顶点C,当时,的值是______.
三、解答题
如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为沿坡面AB向上走到B处测得广告牌顶部C的仰角为,已知山坡AB的坡度:,米,米.:是指坡面的铅直高度BH与水平宽度AH的比
求点B距水平面AE的高度BH;
求广告牌CD的高度.
测角器的高度忽略不计,结果精确到米.参考数据:,
放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?风筝线AD,BD均为线段,?,?,最后结果精确到1米.
1.
D
2.
A
3.
D
4.
D
5.
A
6.
B
7.
D
8.
D
9.
A
10.
A
11.
50??
12.
2??
13.
??
14.
??
15.
或??
16.
??
17.
??
18.
??
19.
18??
20.
??
21.
解:过B作于G,
中,,
,
;
,,,
四边形BHEG是矩形.
由得:,,
,
中,,
.
中,,,
.
.
答:宣传牌CD高约米.??
22.
解:作于H,设米.
,
在直角中,,,,
在直角中,,,,
米,
,
,
小明此时所收回的风筝的长度为:
米.
答:小明此时所收回的风筝线的长度约是8米.??
