苏科版七年级数学上册 第五章 走进图形世界 单元检测试题(word版 含解析)
文档属性
| 名称 | 苏科版七年级数学上册 第五章 走进图形世界 单元检测试题(word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 214.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 08:53:00 | ||
图片预览

文档简介
第五章
走进图形世界
单元检测试题
(满分120分;时间:120分钟)
真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
题号
一
二
三
总分
得分
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
六棱柱有(
)
A.个面
B.个面
C.个面
D.个面
?
2.
用一个平面去截一个几何体,不能截得三角形截面的几何体是(
)
A.圆柱
B.圆锥
C.三棱柱
D.正方体
?
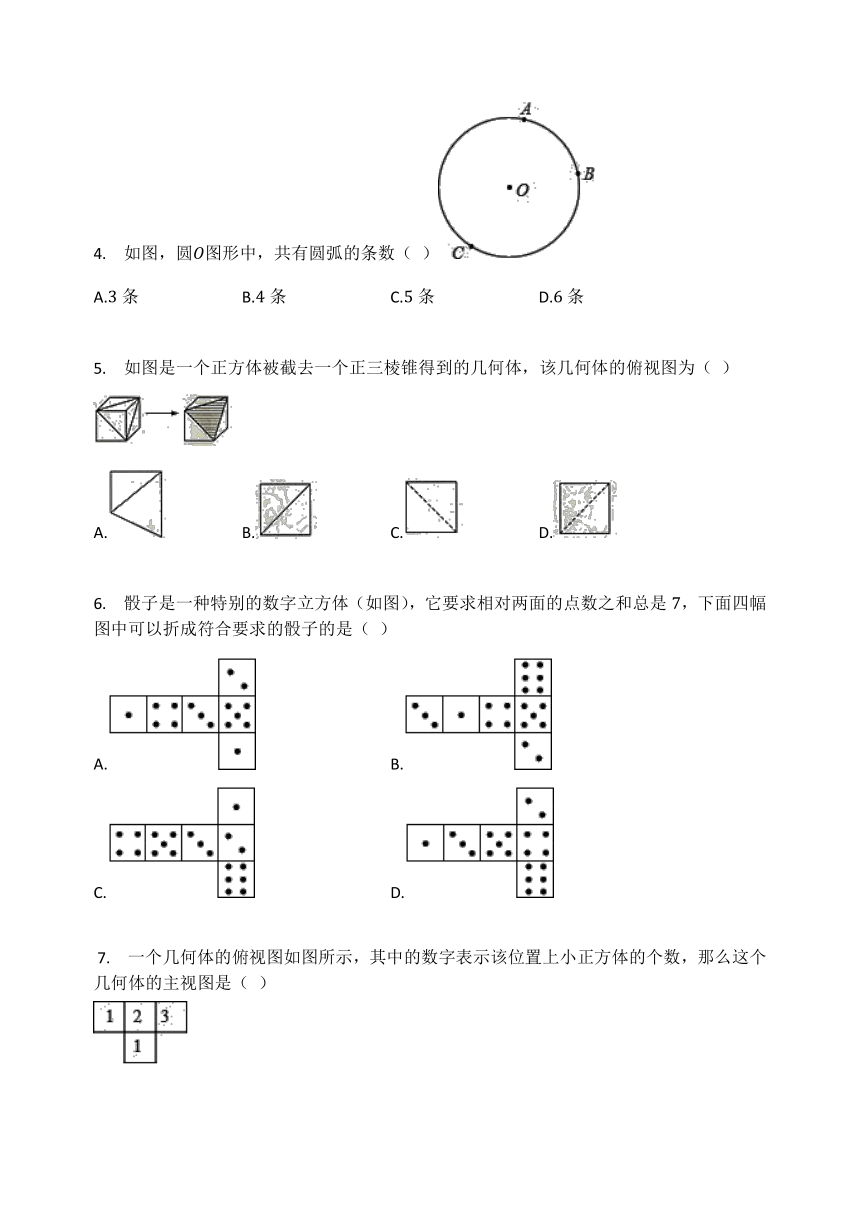
3.
如图所示的立体图形的主视图是?
?
?
?
A.
B.
C.
D.
4.
如图,圆图形中,共有圆弧的条数(
)
A.条
B.条
C.条
D.条
?
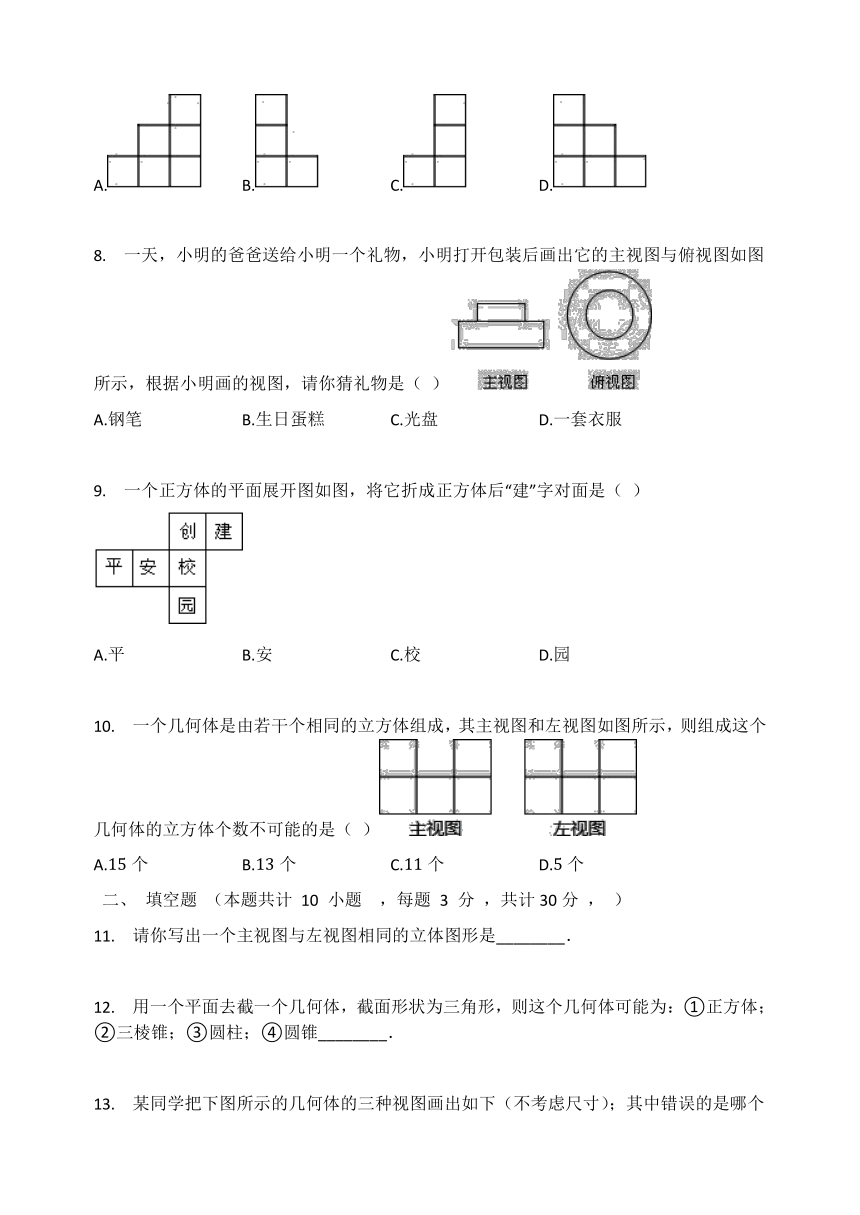
5.
如图是一个正方体被截去一个正三棱锥得到的几何体,该几何体的俯视图为(
)
A.
B.
C.
D.
?
6.
骰子是一种特别的数字立方体(如图),它要求相对两面的点数之和总是,下面四幅图中可以折成符合要求的骰子的是(
)
A.
B.
C.
D.
?7.
一个几何体的俯视图如图所示,其中的数字表示该位置上小正方体的个数,那么这个几何体的主视图是(
)
A.
B.
C.
D.
?
8.
一天,小明的爸爸送给小明一个礼物,小明打开包装后画出它的主视图与俯视图如图所示,根据小明画的视图,请你猜礼物是(
)
A.钢笔
B.生日蛋糕
C.光盘
D.一套衣服
?
9.
一个正方体的平面展开图如图,将它折成正方体后“建”字对面是(
)
A.平
B.安
C.校
D.园
?
10.
一个几何体是由若干个相同的立方体组成,其主视图和左视图如图所示,则组成这个几何体的立方体个数不可能的是(
)
A.个
B.个
C.个
D.个
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
请你写出一个主视图与左视图相同的立体图形是________.
?
12.
用一个平面去截一个几何体,截面形状为三角形,则这个几何体可能为:①正方体;②三棱锥;③圆柱;④圆锥________.
?
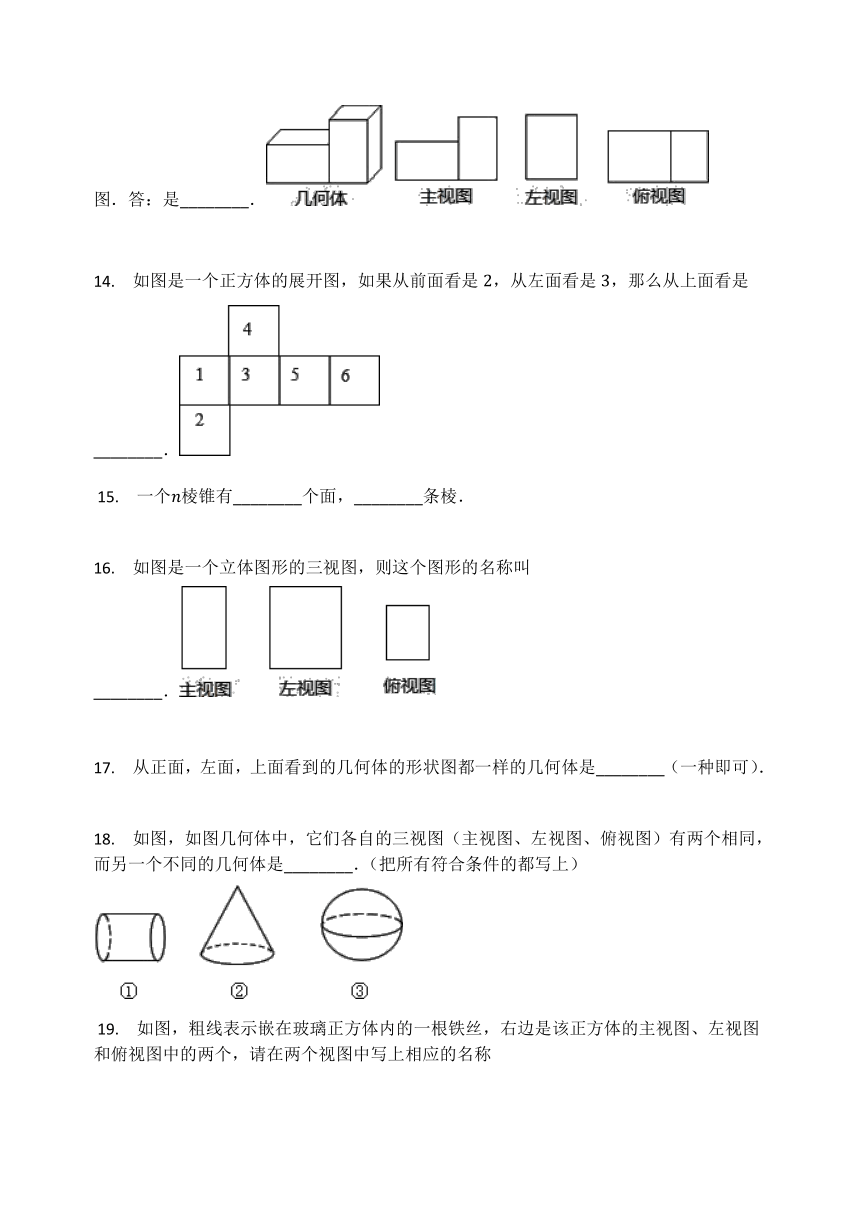
13.
某同学把下图所示的几何体的三种视图画出如下(不考虑尺寸);其中错误的是哪个图.答:是________.
?
14.
如图是一个正方体的展开图,如果从前面看是,从左面看是,那么从上面看是________.
?15.
一个棱锥有________个面,________条棱.
?
16.
如图是一个立体图形的三视图,则这个图形的名称叫________.
?
17.
从正面,左面,上面看到的几何体的形状图都一样的几何体是________(一种即可).
?
18.
如图,如图几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是________.(把所有符合条件的都写上)
?19.
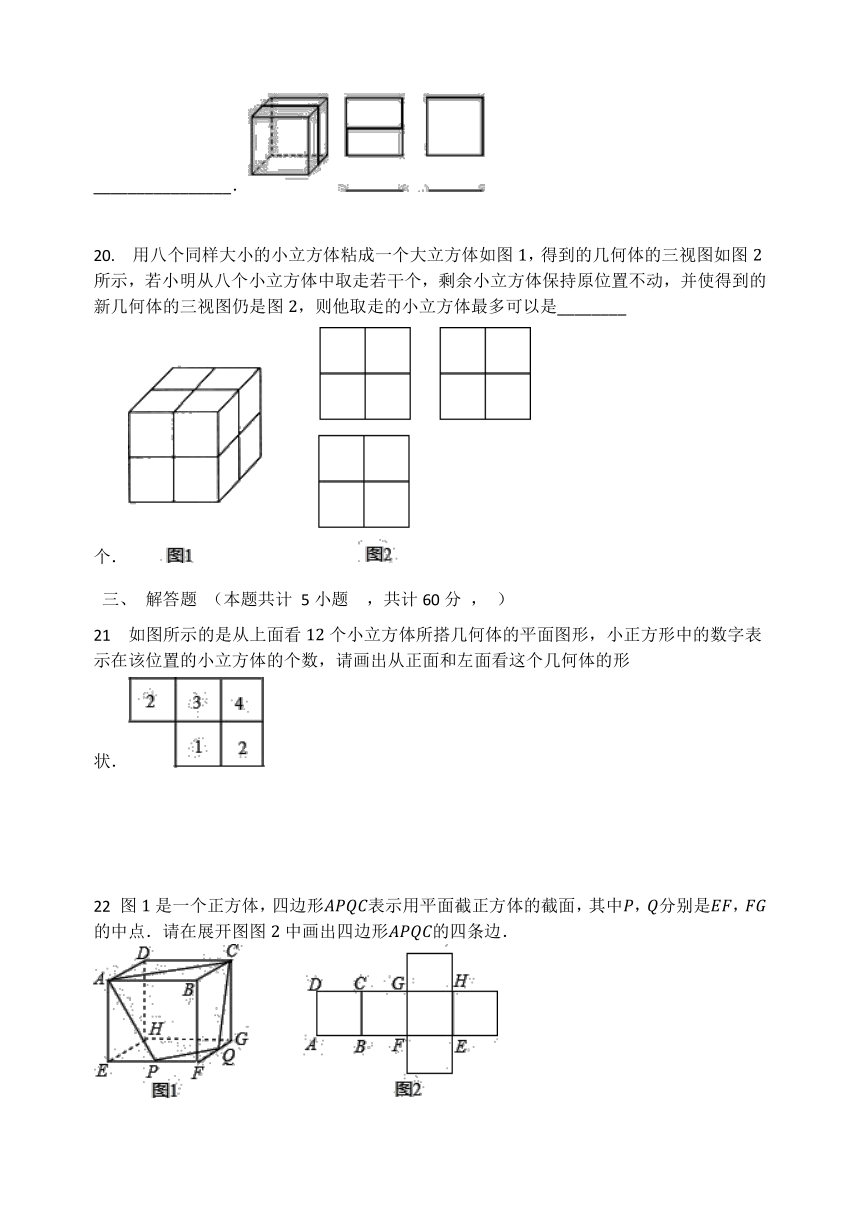
如图,粗线表示嵌在玻璃正方体内的一根铁丝,右边是该正方体的主视图、左视图和俯视图中的两个,请在两个视图中写上相应的名称________________.
?
20.
用八个同样大小的小立方体粘成一个大立方体如图,得到的几何体的三视图如图所示,若小明从八个小立方体中取走若干个,剩余小立方体保持原位置不动,并使得到的新几何体的三视图仍是图,则他取走的小立方体最多可以是________个.
三、
解答题
(本题共计
5小题
,共计60分
,
)
21
如图所示的是从上面看个小立方体所搭几何体的平面图形,小正方形中的数字表示在该位置的小立方体的个数,请画出从正面和左面看这个几何体的形状.
?
22
图是一个正方体,四边形表示用平面截正方体的截面,其中,分别是,的中点.请在展开图图中画出四边形的四条边.
?
23
如图,如果约定用字母表示正方体的侧面,用表示上面,表示底面.请把相应的字母配置在已知加上某些面的记号的正方体的展开图中.
?
24
如图,已知和过点的两条互相垂直的直线、,画出关于直线对称的,再画出关于直线对称的″″″,观察与″″″,这两个三角形具有怎样的对称性?
?
25
小明准备制作一个封闭的正方体盒子,他先用个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请在图中的拼接图形上再接一个正方形,使新拼接的图形经过折叠后能成为一个封闭的正方体盒子.(添加的正方形用阴影表示,只要画出一种即可)
如图所示的几何体是由几个相同的正方体搭成的,请画出它从正面看的形状图.
如图是几个正方体所组成的几何体从上面看的形状图,小正方形中的数字表示该位置小正方体的个数,请画出这个几何体从左面看的形状图.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
C
【解答】
解:六棱柱上下两个底面,侧面是个长方形,所以共有个面.
故选:.
2.
【答案】
A
【解答】
解:、圆柱的截面可能是圆,长方形,符合题意;
、圆锥的截面可能是圆,三角形,不符合题意;
、三棱柱的截面可能是三角形,长方形,不符合题意;
、正方体的截面可能是三角形,或四边形,或五边形,或六边形,不符合题意;
故选.
3.
【答案】
A
【解答】
解:此图的主视图为长方形.
故选.
4.
【答案】
D
【解答】
解:∵
圆弧上任意两点,有两条圆弧,图中有三个点,
∴
,
故选:.
5.
【答案】
B
【解答】
解:从上面看,该几何体的俯视图为是.
故选:.
6.
【答案】
C
【解答】
解:根据正方体的表面展开图,相对的面之间一定相隔一个正方形,
、点与点是相对面,点与点是相对面,点与点是相对面,所以不可以折成符合规则的骰子,故本选项错误;
、点与点是相对面,点与点是相对面,点与点是相对面,所以不可以折成符合规则的骰子,故本选项错误;
、点与点是相对面,点与点是相对面,点与点是相对面,所以可以折成符合规则的骰子,故本选项正确;
、点与点是相对面,点与点是相对面,点与点是相对面,所以不可以折成符合规则的骰子,故本选项错误.
故选.
7.
【答案】
A
【解答】
从正面看去,一共三列,左边有竖列,中间有竖列,右边是竖列.
8.
【答案】
B
【解答】
解:根据主视图为矩形判断出两个几何体是柱体,根据俯视图是圆可判断出这个几何体应该都是圆柱,故选.
9.
【答案】
B
【解答】
解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“平”与“校”是相对面,
“安”与“建”是相对面,
“创”与“园”是相对面.
故选.
10.
【答案】
A
【解答】
解:综合主视图与左视图,第一行第列最多有个,第一行第列最多有个,第一行第列最多有个;
第二行第列最多有个,第二行第列最多有个,第二行第列最多有个;
第三行第列最多有个,第三行第列最多有个,第三行第列最多有个;
所以最多有:(个).不可能为个,
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
圆球(答案不唯一)
【解答】
解:球体的主视图与左视图都为圆.
故答案为:圆球(答案不唯一).
12.
【答案】
①②④
【解答】
①正方体能截出三角形;
②三棱锥能截出三角形;
③圆柱不能截出三角形;
④圆锥沿着母线截几何体可以截出三角形.
故截面可能是三角形的有个.
13.
【答案】
左视图
【解答】
解:根据几何体的摆放位置,主视图和俯视图正确.左视图竖线上下两个矩形,故左视图不正确.
故答案为:左视图.
14.
【答案】
【解答】
解:已知从前面看是,从左面看是,则从后面看是,从右面看是,所以从上面看一定是.
15.
【答案】
,
【解答】
解:棱锥有个面,条棱.
故答案为:,.
16.
【答案】
长方体
【解答】
解:根据三视图可以想象出该物体由四条棱组成,底面是矩形,因此这个立体图形应该是长方体.
17.
【答案】
球(答案不唯一)
【解答】
解:球从正面,左面,上面看到的平面图形为全等的圆,
故答案为:球(答案不唯一).
18.
【答案】
①②
【解答】
解:圆柱主视图和左视图是长方形,俯视图是圆;
圆锥主视图和左视图是三角形、俯视图是带圆心的圆;
故答案为:①②.
19.
【答案】
俯视图,主视图
【解答】
解:细心观察右边的两个图,其中第一个图中间有一条粗线,可判断该图为俯视图;
第二个图的上边和右边是两条粗线,故应该是主视图.
故答案为:俯视图;主视图.
20.
【答案】
【解答】
解:由主视图和左视图可得每一层的每一行每一列都要保留一个立方体,
故取走的小立方体最多可以是个.
具体可参看图形:
故答案为:.
三、
解答题
(本题共计
5
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:作图如下:
【解答】
解:作图如下:
22
【答案】
解:考虑到展开图上有六个顶点没有标出,可想象将展开图折成立体形,并在顶点上标出对应的符号,见图.
根据四边形所在立体图形上的位置,确定其顶点所在的点和棱,以及四条边所在的平面:
顶点:,,在边上,在边上.边在面上,在面上,在面上,在面上.
将上面确定的位置标在展开图上,并在对应平面上连线.需要注意的是,立体图上的,点在展开图上有三个,,点在展开图上有二个,所以在标点连线时必须注意连线所在的平面,连好线的图形如图.
【解答】
解:考虑到展开图上有六个顶点没有标出,可想象将展开图折成立体形,并在顶点上标出对应的符号,见图.
根据四边形所在立体图形上的位置,确定其顶点所在的点和棱,以及四条边所在的平面:
顶点:,,在边上,在边上.边在面上,在面上,在面上,在面上.
将上面确定的位置标在展开图上,并在对应平面上连线.需要注意的是,立体图上的,点在展开图上有三个,,点在展开图上有二个,所以在标点连线时必须注意连线所在的平面,连好线的图形如图.
23
【答案】
解:如图:
【解答】
解:如图:
24
【答案】
解:由关于直线对称的,
得对应点的横坐标相同,纵坐标互为相反数.
由关于直线对称的″″″,
得对应点的纵坐标相同,横坐标互为相反数.
与″″″对应点的横坐标互为相反数,纵坐标互为相反数,
与″″″关于原点对称.
【解答】
解:由关于直线对称的,
得对应点的横坐标相同,纵坐标互为相反数.
由关于直线对称的″″″,
得对应点的纵坐标相同,横坐标互为相反数.
与″″″对应点的横坐标互为相反数,纵坐标互为相反数,
与″″″关于原点对称.
25.
【答案】
解:如图所示;
如图所示;
如图所示:
【解答】
解:如图所示;
如图所示;
如图所示:
走进图形世界
单元检测试题
(满分120分;时间:120分钟)
真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
题号
一
二
三
总分
得分
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
六棱柱有(
)
A.个面
B.个面
C.个面
D.个面
?
2.
用一个平面去截一个几何体,不能截得三角形截面的几何体是(
)
A.圆柱
B.圆锥
C.三棱柱
D.正方体
?
3.
如图所示的立体图形的主视图是?
?
?
?
A.
B.
C.
D.
4.
如图,圆图形中,共有圆弧的条数(
)
A.条
B.条
C.条
D.条
?
5.
如图是一个正方体被截去一个正三棱锥得到的几何体,该几何体的俯视图为(
)
A.
B.
C.
D.
?
6.
骰子是一种特别的数字立方体(如图),它要求相对两面的点数之和总是,下面四幅图中可以折成符合要求的骰子的是(
)
A.
B.
C.
D.
?7.
一个几何体的俯视图如图所示,其中的数字表示该位置上小正方体的个数,那么这个几何体的主视图是(
)
A.
B.
C.
D.
?
8.
一天,小明的爸爸送给小明一个礼物,小明打开包装后画出它的主视图与俯视图如图所示,根据小明画的视图,请你猜礼物是(
)
A.钢笔
B.生日蛋糕
C.光盘
D.一套衣服
?
9.
一个正方体的平面展开图如图,将它折成正方体后“建”字对面是(
)
A.平
B.安
C.校
D.园
?
10.
一个几何体是由若干个相同的立方体组成,其主视图和左视图如图所示,则组成这个几何体的立方体个数不可能的是(
)
A.个
B.个
C.个
D.个
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
请你写出一个主视图与左视图相同的立体图形是________.
?
12.
用一个平面去截一个几何体,截面形状为三角形,则这个几何体可能为:①正方体;②三棱锥;③圆柱;④圆锥________.
?
13.
某同学把下图所示的几何体的三种视图画出如下(不考虑尺寸);其中错误的是哪个图.答:是________.
?
14.
如图是一个正方体的展开图,如果从前面看是,从左面看是,那么从上面看是________.
?15.
一个棱锥有________个面,________条棱.
?
16.
如图是一个立体图形的三视图,则这个图形的名称叫________.
?
17.
从正面,左面,上面看到的几何体的形状图都一样的几何体是________(一种即可).
?
18.
如图,如图几何体中,它们各自的三视图(主视图、左视图、俯视图)有两个相同,而另一个不同的几何体是________.(把所有符合条件的都写上)
?19.
如图,粗线表示嵌在玻璃正方体内的一根铁丝,右边是该正方体的主视图、左视图和俯视图中的两个,请在两个视图中写上相应的名称________________.
?
20.
用八个同样大小的小立方体粘成一个大立方体如图,得到的几何体的三视图如图所示,若小明从八个小立方体中取走若干个,剩余小立方体保持原位置不动,并使得到的新几何体的三视图仍是图,则他取走的小立方体最多可以是________个.
三、
解答题
(本题共计
5小题
,共计60分
,
)
21
如图所示的是从上面看个小立方体所搭几何体的平面图形,小正方形中的数字表示在该位置的小立方体的个数,请画出从正面和左面看这个几何体的形状.
?
22
图是一个正方体,四边形表示用平面截正方体的截面,其中,分别是,的中点.请在展开图图中画出四边形的四条边.
?
23
如图,如果约定用字母表示正方体的侧面,用表示上面,表示底面.请把相应的字母配置在已知加上某些面的记号的正方体的展开图中.
?
24
如图,已知和过点的两条互相垂直的直线、,画出关于直线对称的,再画出关于直线对称的″″″,观察与″″″,这两个三角形具有怎样的对称性?
?
25
小明准备制作一个封闭的正方体盒子,他先用个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请在图中的拼接图形上再接一个正方形,使新拼接的图形经过折叠后能成为一个封闭的正方体盒子.(添加的正方形用阴影表示,只要画出一种即可)
如图所示的几何体是由几个相同的正方体搭成的,请画出它从正面看的形状图.
如图是几个正方体所组成的几何体从上面看的形状图,小正方形中的数字表示该位置小正方体的个数,请画出这个几何体从左面看的形状图.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
C
【解答】
解:六棱柱上下两个底面,侧面是个长方形,所以共有个面.
故选:.
2.
【答案】
A
【解答】
解:、圆柱的截面可能是圆,长方形,符合题意;
、圆锥的截面可能是圆,三角形,不符合题意;
、三棱柱的截面可能是三角形,长方形,不符合题意;
、正方体的截面可能是三角形,或四边形,或五边形,或六边形,不符合题意;
故选.
3.
【答案】
A
【解答】
解:此图的主视图为长方形.
故选.
4.
【答案】
D
【解答】
解:∵
圆弧上任意两点,有两条圆弧,图中有三个点,
∴
,
故选:.
5.
【答案】
B
【解答】
解:从上面看,该几何体的俯视图为是.
故选:.
6.
【答案】
C
【解答】
解:根据正方体的表面展开图,相对的面之间一定相隔一个正方形,
、点与点是相对面,点与点是相对面,点与点是相对面,所以不可以折成符合规则的骰子,故本选项错误;
、点与点是相对面,点与点是相对面,点与点是相对面,所以不可以折成符合规则的骰子,故本选项错误;
、点与点是相对面,点与点是相对面,点与点是相对面,所以可以折成符合规则的骰子,故本选项正确;
、点与点是相对面,点与点是相对面,点与点是相对面,所以不可以折成符合规则的骰子,故本选项错误.
故选.
7.
【答案】
A
【解答】
从正面看去,一共三列,左边有竖列,中间有竖列,右边是竖列.
8.
【答案】
B
【解答】
解:根据主视图为矩形判断出两个几何体是柱体,根据俯视图是圆可判断出这个几何体应该都是圆柱,故选.
9.
【答案】
B
【解答】
解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“平”与“校”是相对面,
“安”与“建”是相对面,
“创”与“园”是相对面.
故选.
10.
【答案】
A
【解答】
解:综合主视图与左视图,第一行第列最多有个,第一行第列最多有个,第一行第列最多有个;
第二行第列最多有个,第二行第列最多有个,第二行第列最多有个;
第三行第列最多有个,第三行第列最多有个,第三行第列最多有个;
所以最多有:(个).不可能为个,
故选.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
圆球(答案不唯一)
【解答】
解:球体的主视图与左视图都为圆.
故答案为:圆球(答案不唯一).
12.
【答案】
①②④
【解答】
①正方体能截出三角形;
②三棱锥能截出三角形;
③圆柱不能截出三角形;
④圆锥沿着母线截几何体可以截出三角形.
故截面可能是三角形的有个.
13.
【答案】
左视图
【解答】
解:根据几何体的摆放位置,主视图和俯视图正确.左视图竖线上下两个矩形,故左视图不正确.
故答案为:左视图.
14.
【答案】
【解答】
解:已知从前面看是,从左面看是,则从后面看是,从右面看是,所以从上面看一定是.
15.
【答案】
,
【解答】
解:棱锥有个面,条棱.
故答案为:,.
16.
【答案】
长方体
【解答】
解:根据三视图可以想象出该物体由四条棱组成,底面是矩形,因此这个立体图形应该是长方体.
17.
【答案】
球(答案不唯一)
【解答】
解:球从正面,左面,上面看到的平面图形为全等的圆,
故答案为:球(答案不唯一).
18.
【答案】
①②
【解答】
解:圆柱主视图和左视图是长方形,俯视图是圆;
圆锥主视图和左视图是三角形、俯视图是带圆心的圆;
故答案为:①②.
19.
【答案】
俯视图,主视图
【解答】
解:细心观察右边的两个图,其中第一个图中间有一条粗线,可判断该图为俯视图;
第二个图的上边和右边是两条粗线,故应该是主视图.
故答案为:俯视图;主视图.
20.
【答案】
【解答】
解:由主视图和左视图可得每一层的每一行每一列都要保留一个立方体,
故取走的小立方体最多可以是个.
具体可参看图形:
故答案为:.
三、
解答题
(本题共计
5
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:作图如下:
【解答】
解:作图如下:
22
【答案】
解:考虑到展开图上有六个顶点没有标出,可想象将展开图折成立体形,并在顶点上标出对应的符号,见图.
根据四边形所在立体图形上的位置,确定其顶点所在的点和棱,以及四条边所在的平面:
顶点:,,在边上,在边上.边在面上,在面上,在面上,在面上.
将上面确定的位置标在展开图上,并在对应平面上连线.需要注意的是,立体图上的,点在展开图上有三个,,点在展开图上有二个,所以在标点连线时必须注意连线所在的平面,连好线的图形如图.
【解答】
解:考虑到展开图上有六个顶点没有标出,可想象将展开图折成立体形,并在顶点上标出对应的符号,见图.
根据四边形所在立体图形上的位置,确定其顶点所在的点和棱,以及四条边所在的平面:
顶点:,,在边上,在边上.边在面上,在面上,在面上,在面上.
将上面确定的位置标在展开图上,并在对应平面上连线.需要注意的是,立体图上的,点在展开图上有三个,,点在展开图上有二个,所以在标点连线时必须注意连线所在的平面,连好线的图形如图.
23
【答案】
解:如图:
【解答】
解:如图:
24
【答案】
解:由关于直线对称的,
得对应点的横坐标相同,纵坐标互为相反数.
由关于直线对称的″″″,
得对应点的纵坐标相同,横坐标互为相反数.
与″″″对应点的横坐标互为相反数,纵坐标互为相反数,
与″″″关于原点对称.
【解答】
解:由关于直线对称的,
得对应点的横坐标相同,纵坐标互为相反数.
由关于直线对称的″″″,
得对应点的纵坐标相同,横坐标互为相反数.
与″″″对应点的横坐标互为相反数,纵坐标互为相反数,
与″″″关于原点对称.
25.
【答案】
解:如图所示;
如图所示;
如图所示:
【解答】
解:如图所示;
如图所示;
如图所示:
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
