苏科版数学八年级上册课件:6.1函数(16张)
文档属性
| 名称 | 苏科版数学八年级上册课件:6.1函数(16张) |
|
|
| 格式 | zip | ||
| 文件大小 | 99.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
6.1
函数
1
2
3
4
1
2
3
-1
-2
-3
-4
-1
-2
-3
O
x
y
学习目标(1分钟)
1.初步掌握函数概念,能判断两个变量间的关系是否可看作函数;
2.根据两个变量间的关系式,给定其中一个量,相应地求出另一个量的值;
自学指导1(4分钟)
认真阅读P75的内容,并思考完成:
1.图4—1反映了变量
与
的关系;
2.图4—1中的两个变量的变化是否有规律呢?你能从图4—1下面的图中说出摩天轮转一圈需要多长时间吗?
3.根据图4—1完成P75的表格(填近似值即可)。
4.对于一个给定的时间t,相应的高度h确定吗?
一个时间对应的高度有几个?
5.P75的问题中的两个变量的关系是通过
形式表示的。(填“图像”、“表格”或“代数表达式”)
时间
高度
图像
自学检测1(3分钟)
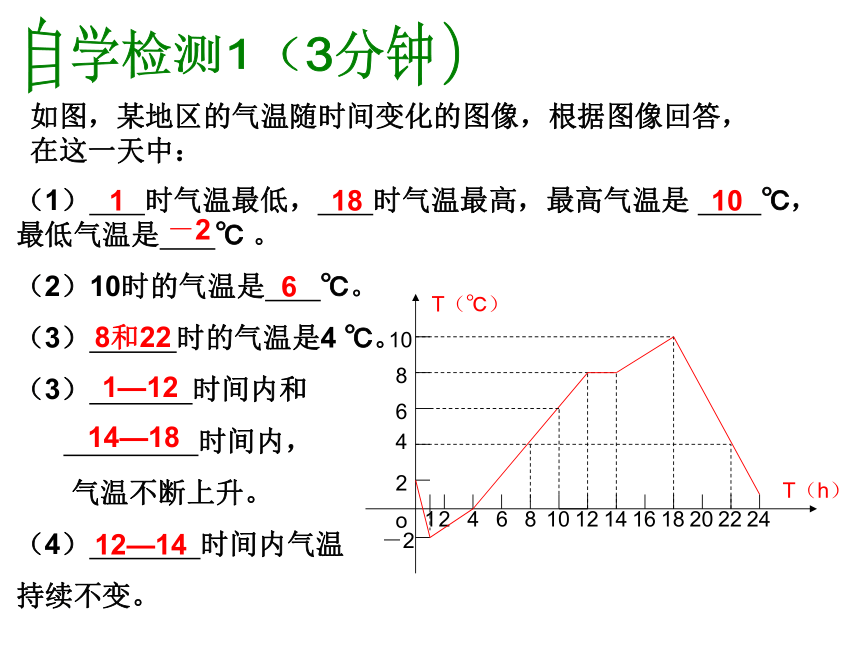
如图,某地区的气温随时间变化的图像,根据图像回答,在这一天中:
(1)
时气温最低,
时气温最高,最高气温是
℃,最低气温是
℃
。
(2)10时的气温是
℃。
(3)
时的气温是4
℃。
(3)
时间内和
时间内,
气温不断上升。
(4)
时间内气温
持续不变。
1
18
-2
10
6
8和22
1—12
14—18
12—14
2
4
6
8
10
12
14
16
18
20
22
24
-2
2
4
6
8
10
o
T(h)
T(℃)
1
自学指导2(6分钟)
认真阅读课本P76“做一做”
,并思考完成:
1.问题(1)反映了变量
与
的关系,两个变量的关系是通过
的形式表示的
(填“图像”、“表格”或“代数表达式”)
。
2.完成P76问题(1)的表格。
3.问题(2)反映了变量
与
的关系,两个变量的关系是通过
的形式表示的(填“图像”、“表格”或“代数表达式”)
。
4.完成P76问题(2)中的两个问题。
层数
总数
表格
热力学温度
摄氏温度
代数表达式
认真阅读课本P76中“函数的概念及做一做”的内容,脱开课本回答:
1.两个问题中,自变量给定一个值,因变量只有
个值与之对应。
2.一般地,在某个变化过程中,有两个变量x和y,如果(在某个范围内)给定一个x值,相应地就确定了一个y值,那么我们称y是x的
,其中x是
,y是
.
3.完成P77—78随堂练习-1T和知识技能-1T。
一
函数
自变量
因变量
自学指导3(6分钟)
函数的概念与表示法
1.概念:一般地,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定了一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量。
1.当自变量x给定一个值,函数y有且只有唯一的值与其对应。如:y2=x,当x=4时,y=2或-2,故y不是x的函数。
注意:
2.函数的解析式是一个等式(或者说是一个含有两个未知数的方程),左边是因变量,右边是含自变量的代数式;
2.函数的表示法:图像法、列表法、解析法。
x
y
O
x
y
O
上面两个图像可以看作函数的图像吗?
(1)
(2)
a
b
-b
返回
自学检测3(10分钟)
1.在圆的周长公式C=2
R中,下列判断正确的是(
)
A.C,
,R是变量,2是常量
B.
R是变量,
C,
是常量
C.C是变量,R,
是常量
D.C,R是变量,
,2是常量
2.长方体盒子高为10cm,底面是正方形,这个长方体的体积V(cm3)与底面边长a(cm)的关系式为
,其中
是常量,
是自变量,
是因变量,
是
的函数。
3.用总长为60m的篱笆围成矩形场地,矩形的面积S(m2)与一边长a
(m)之间的关系式为
,
其中
是常量,
是自变量,
是因变量,
是
的函数。
D
V=10a2
10
a
V
V
a
S=a(30-a)
30
a
S
S
a
6.已知x、y满足关系式2x-y=1,用含x的代数式表示y,
则y=
,当x=1时,y=
,当x=-3时,y=
。
7.某工厂现在年产值为50(万元),计划今年后每年增长10万元,年产值y(万元)与年数x的函数关系式是
当x=5时y=
(万元)
2x-1
1
-7
y=10x+50
100
4.下列关于变量x、y的关系中:①y=2x+1,②y=
︱x︱
,
③
y2=10
-
2x
;其中表示y是x的函数关系是(
)
A.
①
②
③
B
.①
②
C.
①
③
D
.
②
③
5.下列图中,y不是x的函数的是(
)
x
y
o
x
y
o
x
y
o
x
y
o
A
B
C
D
B
D
自学指导4(5分钟)
想一想:
下列函数中,自变量x分别取何值时函数y有意义?
(1)y=x+1
(2)y=
2
x-1
(3)y=
(4)y=
+
2
x-1
(5)y=(n-2)180°
(n为多边形的边数,y为多边形的内角和。)
解:(1)x为任意实数;
(2)因为x-1≠0,所以x≠1;
(3)因为x-2≥0,所以x≥2;
(4)因为2
-
x
≥0且x-1≠0
,所以x≤2且x≠1
;
(5)因为n为多边形的边数,所以n为大于或等于3的整数。
确定自变量的取值范围应注意:
1.自变量的取值必须使函数的表达式有意义:
(1)分母不能等于0;
(2)被开方数必须大于或等于0。
2.函数表达式表示实际问题时,自变量的取值必须使实际问题有意义
自学检测4(4分钟)
1.函数y=
中,自变量x的取值范围是(
)
A.x>
-2
B.x≥-2
C.x≠
-2
D.x≤
-2
2.函数y=
中,自变量x的取值范围是(
)
A.x<
B.x≠
C.x≠
D.x>
3.函数y=
中,自变量x的取值范围是(
)
A.x≥
-3
B.x>-3
C.x≠
0且x≠
-3
D.x≥
-3且x
≠0
B
C
D
4.若等腰三角形的周长为50厘米,底边长为x厘米,一腰长为y厘米,则y与x的函数关系式及自变量x的取值范围是(
)
A.y=50-2x(0<x<50)
B.
y=50-2x(0<x<25)
C.y=
(50
-x)(0<x<50)
D.y=
(50
-x)(0<x<25)
5.一个正方形的边长为5cm,它的边长减少xcm,后得到的新的正方形的周长为ycm,写出y与x的关系式,并指出自变量的取值范围。
D
解:y=4(5-x)(0<x<5)
小结(1分钟)
1.函数概念:一般地,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定了一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量;
2.函数的表示法:图像法、列表法、解析式法;
3.自变量取值范围的确定。
当堂训练
(7分钟)
6.1
函数
1
2
3
4
1
2
3
-1
-2
-3
-4
-1
-2
-3
O
x
y
学习目标(1分钟)
1.初步掌握函数概念,能判断两个变量间的关系是否可看作函数;
2.根据两个变量间的关系式,给定其中一个量,相应地求出另一个量的值;
自学指导1(4分钟)
认真阅读P75的内容,并思考完成:
1.图4—1反映了变量
与
的关系;
2.图4—1中的两个变量的变化是否有规律呢?你能从图4—1下面的图中说出摩天轮转一圈需要多长时间吗?
3.根据图4—1完成P75的表格(填近似值即可)。
4.对于一个给定的时间t,相应的高度h确定吗?
一个时间对应的高度有几个?
5.P75的问题中的两个变量的关系是通过
形式表示的。(填“图像”、“表格”或“代数表达式”)
时间
高度
图像
自学检测1(3分钟)
如图,某地区的气温随时间变化的图像,根据图像回答,在这一天中:
(1)
时气温最低,
时气温最高,最高气温是
℃,最低气温是
℃
。
(2)10时的气温是
℃。
(3)
时的气温是4
℃。
(3)
时间内和
时间内,
气温不断上升。
(4)
时间内气温
持续不变。
1
18
-2
10
6
8和22
1—12
14—18
12—14
2
4
6
8
10
12
14
16
18
20
22
24
-2
2
4
6
8
10
o
T(h)
T(℃)
1
自学指导2(6分钟)
认真阅读课本P76“做一做”
,并思考完成:
1.问题(1)反映了变量
与
的关系,两个变量的关系是通过
的形式表示的
(填“图像”、“表格”或“代数表达式”)
。
2.完成P76问题(1)的表格。
3.问题(2)反映了变量
与
的关系,两个变量的关系是通过
的形式表示的(填“图像”、“表格”或“代数表达式”)
。
4.完成P76问题(2)中的两个问题。
层数
总数
表格
热力学温度
摄氏温度
代数表达式
认真阅读课本P76中“函数的概念及做一做”的内容,脱开课本回答:
1.两个问题中,自变量给定一个值,因变量只有
个值与之对应。
2.一般地,在某个变化过程中,有两个变量x和y,如果(在某个范围内)给定一个x值,相应地就确定了一个y值,那么我们称y是x的
,其中x是
,y是
.
3.完成P77—78随堂练习-1T和知识技能-1T。
一
函数
自变量
因变量
自学指导3(6分钟)
函数的概念与表示法
1.概念:一般地,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定了一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量。
1.当自变量x给定一个值,函数y有且只有唯一的值与其对应。如:y2=x,当x=4时,y=2或-2,故y不是x的函数。
注意:
2.函数的解析式是一个等式(或者说是一个含有两个未知数的方程),左边是因变量,右边是含自变量的代数式;
2.函数的表示法:图像法、列表法、解析法。
x
y
O
x
y
O
上面两个图像可以看作函数的图像吗?
(1)
(2)
a
b
-b
返回
自学检测3(10分钟)
1.在圆的周长公式C=2
R中,下列判断正确的是(
)
A.C,
,R是变量,2是常量
B.
R是变量,
C,
是常量
C.C是变量,R,
是常量
D.C,R是变量,
,2是常量
2.长方体盒子高为10cm,底面是正方形,这个长方体的体积V(cm3)与底面边长a(cm)的关系式为
,其中
是常量,
是自变量,
是因变量,
是
的函数。
3.用总长为60m的篱笆围成矩形场地,矩形的面积S(m2)与一边长a
(m)之间的关系式为
,
其中
是常量,
是自变量,
是因变量,
是
的函数。
D
V=10a2
10
a
V
V
a
S=a(30-a)
30
a
S
S
a
6.已知x、y满足关系式2x-y=1,用含x的代数式表示y,
则y=
,当x=1时,y=
,当x=-3时,y=
。
7.某工厂现在年产值为50(万元),计划今年后每年增长10万元,年产值y(万元)与年数x的函数关系式是
当x=5时y=
(万元)
2x-1
1
-7
y=10x+50
100
4.下列关于变量x、y的关系中:①y=2x+1,②y=
︱x︱
,
③
y2=10
-
2x
;其中表示y是x的函数关系是(
)
A.
①
②
③
B
.①
②
C.
①
③
D
.
②
③
5.下列图中,y不是x的函数的是(
)
x
y
o
x
y
o
x
y
o
x
y
o
A
B
C
D
B
D
自学指导4(5分钟)
想一想:
下列函数中,自变量x分别取何值时函数y有意义?
(1)y=x+1
(2)y=
2
x-1
(3)y=
(4)y=
+
2
x-1
(5)y=(n-2)180°
(n为多边形的边数,y为多边形的内角和。)
解:(1)x为任意实数;
(2)因为x-1≠0,所以x≠1;
(3)因为x-2≥0,所以x≥2;
(4)因为2
-
x
≥0且x-1≠0
,所以x≤2且x≠1
;
(5)因为n为多边形的边数,所以n为大于或等于3的整数。
确定自变量的取值范围应注意:
1.自变量的取值必须使函数的表达式有意义:
(1)分母不能等于0;
(2)被开方数必须大于或等于0。
2.函数表达式表示实际问题时,自变量的取值必须使实际问题有意义
自学检测4(4分钟)
1.函数y=
中,自变量x的取值范围是(
)
A.x>
-2
B.x≥-2
C.x≠
-2
D.x≤
-2
2.函数y=
中,自变量x的取值范围是(
)
A.x<
B.x≠
C.x≠
D.x>
3.函数y=
中,自变量x的取值范围是(
)
A.x≥
-3
B.x>-3
C.x≠
0且x≠
-3
D.x≥
-3且x
≠0
B
C
D
4.若等腰三角形的周长为50厘米,底边长为x厘米,一腰长为y厘米,则y与x的函数关系式及自变量x的取值范围是(
)
A.y=50-2x(0<x<50)
B.
y=50-2x(0<x<25)
C.y=
(50
-x)(0<x<50)
D.y=
(50
-x)(0<x<25)
5.一个正方形的边长为5cm,它的边长减少xcm,后得到的新的正方形的周长为ycm,写出y与x的关系式,并指出自变量的取值范围。
D
解:y=4(5-x)(0<x<5)
小结(1分钟)
1.函数概念:一般地,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定了一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量;
2.函数的表示法:图像法、列表法、解析式法;
3.自变量取值范围的确定。
当堂训练
(7分钟)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
