4.5.1-4.5.2函数的零点和方程的解、二分法求方程近似解-课件(共20张PPT)
文档属性
| 名称 | 4.5.1-4.5.2函数的零点和方程的解、二分法求方程近似解-课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 17:11:49 | ||
图片预览






文档简介
(共20张PPT)
4.5.1~4.5.2
函数的零点与方程的解
用二分法求方程的近似解
新高考新教材
高中数第一册第四章指数函数与对数函数
2020/12/1
我们已经学习了用二次函数的观点认识一元二次方程,知道一元二次方程的实数根就是相应二次函数的零点.
情境引入
2
1
1
-2
2
-1
3
4
-1
-2
-3
-4
0
y
x
函数y=f(x)的零点就是方程f(x)=0的实数解x,也就是函
数y=f(x)的图象与x轴的公共点的横坐标。
像lnx+2x-6=0这样不能用公式求解的方程,是否也能采用类似的方法,用相应的函数研究它的解的情况呢?
一般地,对于不能用公式求解的方程f(x)
=0,我们可以把它与相应的函数y=f(x)联系起来,利用函数的图象和性质找出零点,从而得到方程的解。
2
1
1
-2
2
-1
3
4
-1
-2
-3
-4
0
y
x
在零点附近,函数图象是连续不断的,并且“穿过”x轴。
函数在端点x=2和x
=4的取值异号,即
f(2)
f(4)<0,
函数
f(x)=x2-2x-3在区间(2,
4)内有零点x
=3,
它是方程x2-2x-3=0的一个根。
函数f(x)=x2-2x-3在(-2,
0)内有零点x=-1,它是方程x2-2x-3=0的另一个根。
同样地,f(-2)f(0)<0
如果函数
y=f(x)
在区间[a,b]上的图象是连续不断的一条曲线,且有
f(a)
f(b)<0
,那么函数
y=f(x)在区间
(a,b)
内至少一个零点,即存在
c
∈
(a,b),使得
f(c)
=0,这个c也就是方程
f(x)=0
的解。
函数零点存在定理
0
y
x
0
y
x
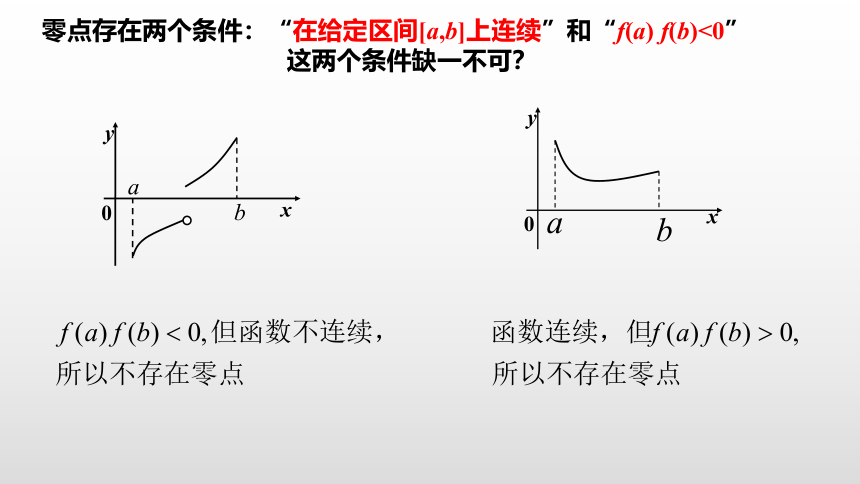
零点存在两个条件:“在给定区间[a,b]上连续”和“f(a)
f(b)<0”
这两个条件缺一不可?
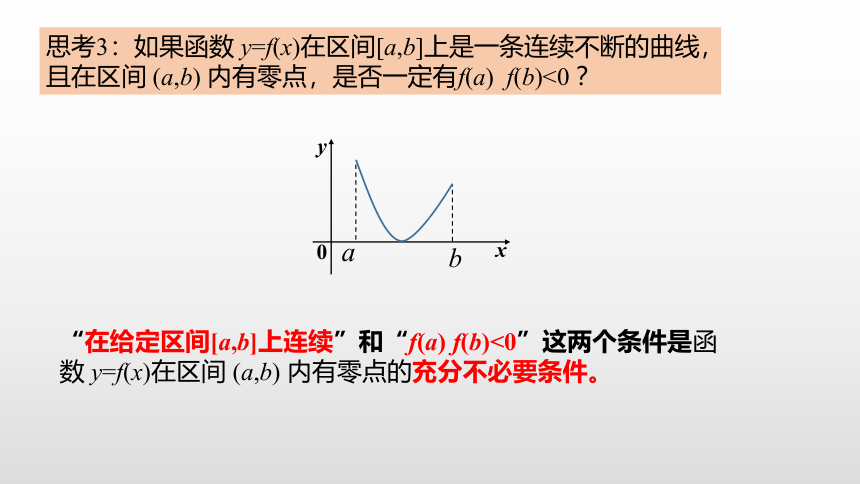
思考3:如果函数
y=f(x)在区间[a,b]上是一条连续不断的曲线,且在区间
(a,b)
内有零点,是否一定有f(a)
f(b)<0
?
x
y
0
“在给定区间[a,b]上连续”和“f(a)
f(b)<0”这两个条件是函数
y=f(x)在区间
(a,b)
内有零点的充分不必要条件。
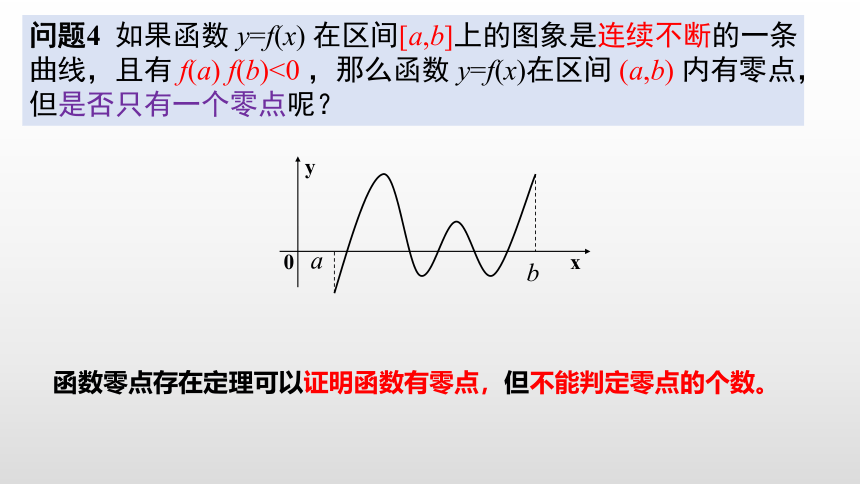
问题4
如果函数
y=f(x)
在区间[a,b]上的图象是连续不断的一条曲线,且有
f(a)
f(b)<0
,那么函数
y=f(x)在区间
(a,b)
内有零点,但是否只有一个零点呢?
0
y
x
函数零点存在定理可以证明函数有零点,但不能判定零点的个数。
2020/12/1
f(2)<0,
f(3)>0,
即f(2)
f(3)<0,
由函数零点存在定理可知,这个函数在区间(2,3)内至少有一个零点。
.
.
.
.
.
.
.
.
.
x
0
-2
-4
-6
10
5
y
2
4
10
8
6
12
14
8
7
6
4
3
2
1
9
假设我们知道函数
在区间(2,3)内存在一个零点,那么我们怎么求出这个零点呢?
?
一个直观的想法是:如果能将零点所在的范围尽量的缩小,那么在一定精确度的要求下,就可以得到符合要求的零点的近似值.为了方便,可以通过取中点的方法,逐步缩小零点的范围.
4.5.2用二分求方程的近似解
函数
在区间(2,3)上有零点,并且
,取(2,3)的中点2.5,利用计算器求出
.因为
,所
以零点在区间(2.5,3)之间;再取区间(2.5,3)的中点2.75,出
,则零点在区间(2.5,2.75)之间…
?
?
?
?
?
当
时,
区间
任意一
个值都可以作为零
点近似值.
?
?
①③
2和1
C
【常见函数的零点】
一个零点
无零点
?
?
?
两个零点
一个零点
无零点
无零点
一个零点1
?
?
一个零点0
无零点
4.5.1~4.5.2
函数的零点与方程的解
用二分法求方程的近似解
新高考新教材
高中数第一册第四章指数函数与对数函数
2020/12/1
我们已经学习了用二次函数的观点认识一元二次方程,知道一元二次方程的实数根就是相应二次函数的零点.
情境引入
2
1
1
-2
2
-1
3
4
-1
-2
-3
-4
0
y
x
函数y=f(x)的零点就是方程f(x)=0的实数解x,也就是函
数y=f(x)的图象与x轴的公共点的横坐标。
像lnx+2x-6=0这样不能用公式求解的方程,是否也能采用类似的方法,用相应的函数研究它的解的情况呢?
一般地,对于不能用公式求解的方程f(x)
=0,我们可以把它与相应的函数y=f(x)联系起来,利用函数的图象和性质找出零点,从而得到方程的解。
2
1
1
-2
2
-1
3
4
-1
-2
-3
-4
0
y
x
在零点附近,函数图象是连续不断的,并且“穿过”x轴。
函数在端点x=2和x
=4的取值异号,即
f(2)
f(4)<0,
函数
f(x)=x2-2x-3在区间(2,
4)内有零点x
=3,
它是方程x2-2x-3=0的一个根。
函数f(x)=x2-2x-3在(-2,
0)内有零点x=-1,它是方程x2-2x-3=0的另一个根。
同样地,f(-2)f(0)<0
如果函数
y=f(x)
在区间[a,b]上的图象是连续不断的一条曲线,且有
f(a)
f(b)<0
,那么函数
y=f(x)在区间
(a,b)
内至少一个零点,即存在
c
∈
(a,b),使得
f(c)
=0,这个c也就是方程
f(x)=0
的解。
函数零点存在定理
0
y
x
0
y
x
零点存在两个条件:“在给定区间[a,b]上连续”和“f(a)
f(b)<0”
这两个条件缺一不可?
思考3:如果函数
y=f(x)在区间[a,b]上是一条连续不断的曲线,且在区间
(a,b)
内有零点,是否一定有f(a)
f(b)<0
?
x
y
0
“在给定区间[a,b]上连续”和“f(a)
f(b)<0”这两个条件是函数
y=f(x)在区间
(a,b)
内有零点的充分不必要条件。
问题4
如果函数
y=f(x)
在区间[a,b]上的图象是连续不断的一条曲线,且有
f(a)
f(b)<0
,那么函数
y=f(x)在区间
(a,b)
内有零点,但是否只有一个零点呢?
0
y
x
函数零点存在定理可以证明函数有零点,但不能判定零点的个数。
2020/12/1
f(2)<0,
f(3)>0,
即f(2)
f(3)<0,
由函数零点存在定理可知,这个函数在区间(2,3)内至少有一个零点。
.
.
.
.
.
.
.
.
.
x
0
-2
-4
-6
10
5
y
2
4
10
8
6
12
14
8
7
6
4
3
2
1
9
假设我们知道函数
在区间(2,3)内存在一个零点,那么我们怎么求出这个零点呢?
?
一个直观的想法是:如果能将零点所在的范围尽量的缩小,那么在一定精确度的要求下,就可以得到符合要求的零点的近似值.为了方便,可以通过取中点的方法,逐步缩小零点的范围.
4.5.2用二分求方程的近似解
函数
在区间(2,3)上有零点,并且
,取(2,3)的中点2.5,利用计算器求出
.因为
,所
以零点在区间(2.5,3)之间;再取区间(2.5,3)的中点2.75,出
,则零点在区间(2.5,2.75)之间…
?
?
?
?
?
当
时,
区间
任意一
个值都可以作为零
点近似值.
?
?
①③
2和1
C
【常见函数的零点】
一个零点
无零点
?
?
?
两个零点
一个零点
无零点
无零点
一个零点1
?
?
一个零点0
无零点
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
