人教版数学八年级上册 13.2作对称图形同步测试题(一)Word版含答案
文档属性
| 名称 | 人教版数学八年级上册 13.2作对称图形同步测试题(一)Word版含答案 |
|
|
| 格式 | doc | ||
| 文件大小 | 164.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 11:48:04 | ||
图片预览


文档简介
作对称图形同步测试题(一)
一.选择题
1.若点A(m,n)和点B(5,﹣7)关于x轴对称,则m,n的值是( )
A.5,7 B.5,﹣7 C.﹣5,7 D.﹣5,﹣7
2.在平面直角坐标系中,已知点A(﹣2a,6)与B(4,b+2)关于x轴对称,则a,b的值为( )
A.a=2,b=﹣8 B.a=2,b=8 C.a=﹣2,b=8 D.a=﹣2,b=﹣8
3.点(3,2)关于x轴的对称点为( )
A. C.
4.在平面直角坐标系中,点P(2,1)向右平移3个单位得到点P1,点P1关于x轴的对称点是点P2,则点P2的坐标是( )
A. C.
5.点A(a﹣3,﹣1)与点B(2,b+2)关于x轴对称,则a,b的值分别是( )
A.a=1,b=﹣3 B.a=1,b=﹣1 C.a=5,b=﹣3 D.a=5,b=﹣1
6.已知点A(m+2,﹣3),B(﹣2,n﹣4)关于y轴对称,则m﹣n的值为( )
A.4 B.1 C.﹣1 D.0
7.如图,△ABC顶点B的坐标是(﹣5,2),先把△ABC向右平移3个单位得到△A1B1C1,再作△A1B1C1关于y轴的对称图形△A2B2C2,则顶点B2的坐标是( )
A. C.
8.已知点A(a,3),B(﹣3,b),若点A、B关于x轴对称,则点P(﹣a,﹣b)在第_____象限,若点A、B关于y轴对称,则点P(﹣a,﹣b)在第_____象限.且平行于y轴的直线上;
②当m≠0时,点P(m2,﹣m)在第四象限;
③与点(﹣3,4)关于y轴对称的点的坐标是(﹣3,﹣4);
④在第一象限的点N到x轴的距离是1,到y轴的距离是2,则点N的坐标为(2,1).
其中正确的是( )
A.①③ B.②④ C.①④ D.②③
10.如图,在3×3的正方形网格中有四个格点A,B,C,D,以其中一个点为原点,网格线所在的直线为坐标轴,建立平面直角坐标系,使其余的三个点中有两个点关于一条坐标轴对称,则原点为( )
A.A点 B.B点 C.C点 D.D点
二.填空题
11.在平面直角坐标系中,点A(2,﹣3)与点B(a,b)关于y轴对称,则a﹣b= .
12.已知在平面直角坐标系中点A的坐标为(﹣1,0),则A点关于y轴对称的点坐标为 .
13.若点A(a,2)与B(3,b)关于x轴对称,则a﹣b= .
14.已知点M(a+3,﹣5)和N(2,b﹣1)关于x轴对称,则ab的值为 .
15.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(a,b),经过第1次变换后所得的A1坐标是(a,﹣b),则经过第2020次变换后所得的点A2020坐标是 .
三.解答题
16.如图,在4×5的网格中,A,B,C均为格点(最小正方形的顶点).在图1、图2中分别画一个与△ABC成轴对称的格点三角形,所画的两个三角形的位置不同.
17.如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上,如果用(1,0)表示C点的位置,用(4,1)表示B点的位置.
(1)画出直角坐标系xOy,写出点A的坐标;
(2)作出△ABC关于x轴对称的△A′B′C′,并直接写出点A′,B′的坐标.
18.△ABC在平面直角坐标系xOy中的位置如图所示.
(1)画出△ABC关于y轴对称的△A1B1C1,并写出各顶点坐标;
(2)在(1)的基础上,将△A1B1C1先向右平移3个单位,再向下平移2个单位得△A2B2C2,作出△A2B2C2,直接写出点(,﹣)与△A2B2C2的位置关系.
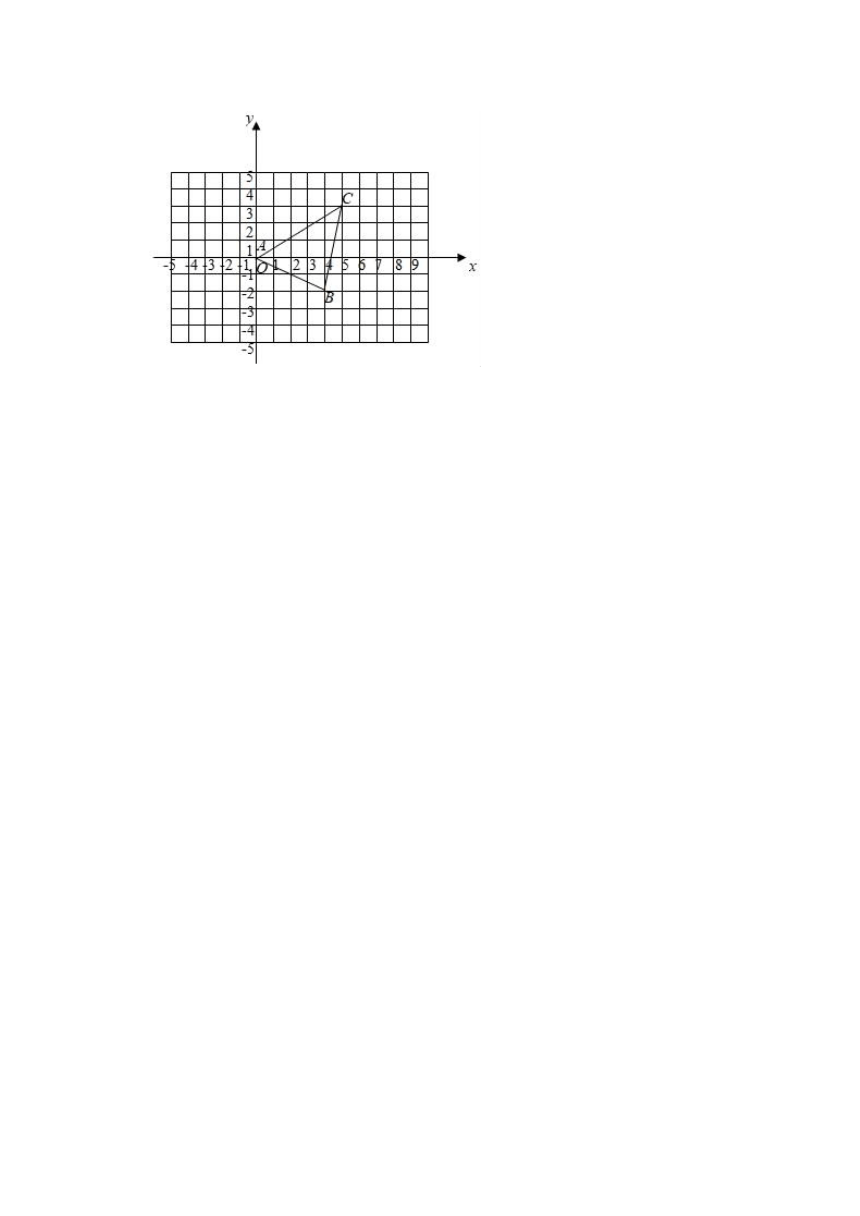
19.如图,△ABC的三个顶点坐标分别为A(0,0),B(4,﹣2),C(5,3),将三角形三个顶点的坐标作如下变化:
(1)画出△ABC关于x轴对称的图形;
(2)求△ABC的面积.
参考答案与试题解析
一.选择题
1.【解答】解:∵点A(m,n)和点B(5,﹣7)关于x轴对称,
∴m=5,n=7,
故选:A.
2.【解答】解:∵点A(﹣2a,6)与B(4,b+2)关于x轴对称,
∴﹣2a=4,b+2=﹣6,
解得:a=﹣2,b=﹣8,
故选:D.
3.【解答】解:点(3,2)关于x轴的对称点为:(3,﹣2).
故选:B.
4.【解答】解:∵将点P(2,1)向右平移3个单位得到点P1,
∴点P1的坐标是(5,1),
∴点P1关于x轴的对称点P2的坐标是(5,﹣1).
故选:B.
5.【解答】解:(2,b+2)与点(a﹣3,﹣1)关于x轴对称,得
a﹣3=2,b+2=1.
解得a=5,b=﹣1,
故选:D.
6.【解答】解:∵点A(m+2,﹣3),B(﹣2,n﹣4)关于y轴对称,
∴m+2=2,n﹣4=﹣3,
解得:m=0,n=1,
则m﹣n=﹣1.
故选:C.
7.【解答】解:∵顶点B的坐标是(﹣5,2),将其向右平移3个单位得到顶点B1,
∴顶点B1的坐标为(﹣2,2).
又∵顶点B2和顶点B1关于y轴对称,
∴顶点B2的坐标为(2,2).
故选:C.
8.【解答】解:∵点A(a,3),B(﹣3,b)关于x轴对称,
∴a=﹣3,b=﹣3,
∴﹣a>0,﹣b>0,
∴点P(﹣a,﹣b)在第一象限,
∵点A(a,3),B(﹣3,b)关于y轴对称,
∴a=3,b=3,
∴﹣a<0,﹣b<0,
∴点P(﹣a,﹣b)在第三象限,
故选:A.
9.【解答】解:①横坐标为﹣3的点在经过点(﹣3,0)且平行于y轴的直线上,故正确;
②当m≠0时,点P(m2,﹣m)在第四象限或第一象限,故错误;
③与点(﹣3,4)关于y轴对称的点的坐标是(3,4),故错误;
④在第一象限的点N到x轴的距离是1,到y轴的距离是2,则点N的坐标为(2,1),故正确.
故选:C.
10.【解答】解:如图所示:
以B点为原点,建立平面直角坐标系,此时存在两个点A,C关于x轴对称,
故选:B.
二.填空题(共5小题)
11.【解答】解:∵点A(2,﹣3)与点B(a,b)关于y轴对称,
∴a=﹣2,b=﹣3,
∴a﹣b=﹣2+3=1.
故答案为:1.
12.【解答】解:∵平面直角坐标系中点A的坐标为(﹣1,0),
∴A点关于y轴对称的点坐标为(1,0),
故答案为:(1,0).
13.【解答】解:∵点A(a,2)与点B(3,b)关于x轴对称,
∴a=3,b=﹣2,
∴a﹣b=3﹣(﹣2)=3+2=5,
故答案为:5.
14.【解答】解:∵点M(a+3,﹣5)和N(2,b﹣1)关于x轴对称,
∴a+3=2,b﹣1=5.
解得a=﹣1,b=6,
∴ab=(﹣1)6=1,
故答案为:1.
15.【解答】解:点A第一次关于x轴对称后在第四象限,
点A第二次关于y轴对称后在第三象限,
点A第三次关于x轴对称后在第二象限,
点A第四次关于y轴对称后在第一象限,
即点A回到原始位置,
所以,每四次对称为一个循环组依次循环,
∵2020÷4=505,
∴经过第2020次变换后所得的A点与第一次变换的位置相同,在第四象限,
坐标为(a,﹣b).
故答案为(a,﹣b).
三.解答题(共4小题)
16.【解答】解:如图所示:△ABD即为所求.
.
17.【解答】解:(1)如图所示:A(0,2);
(2)如图所示:△A′B′C′即为所求,
A′(0,﹣2),B′(4,﹣1).
18.【解答】解:(1)如图所示:△A1B1C1即为所求,
A1(2,3),B1(1,1),C1(0,2);
(2)如图所示:△A2B2C2即为所求,
点(,﹣)是所在小正方形对角线交点,正好在△A2B2C2的边C2B2上.
19.【解答】解:(1)如图所示
一.选择题
1.若点A(m,n)和点B(5,﹣7)关于x轴对称,则m,n的值是( )
A.5,7 B.5,﹣7 C.﹣5,7 D.﹣5,﹣7
2.在平面直角坐标系中,已知点A(﹣2a,6)与B(4,b+2)关于x轴对称,则a,b的值为( )
A.a=2,b=﹣8 B.a=2,b=8 C.a=﹣2,b=8 D.a=﹣2,b=﹣8
3.点(3,2)关于x轴的对称点为( )
A. C.
4.在平面直角坐标系中,点P(2,1)向右平移3个单位得到点P1,点P1关于x轴的对称点是点P2,则点P2的坐标是( )
A. C.
5.点A(a﹣3,﹣1)与点B(2,b+2)关于x轴对称,则a,b的值分别是( )
A.a=1,b=﹣3 B.a=1,b=﹣1 C.a=5,b=﹣3 D.a=5,b=﹣1
6.已知点A(m+2,﹣3),B(﹣2,n﹣4)关于y轴对称,则m﹣n的值为( )
A.4 B.1 C.﹣1 D.0
7.如图,△ABC顶点B的坐标是(﹣5,2),先把△ABC向右平移3个单位得到△A1B1C1,再作△A1B1C1关于y轴的对称图形△A2B2C2,则顶点B2的坐标是( )
A. C.
8.已知点A(a,3),B(﹣3,b),若点A、B关于x轴对称,则点P(﹣a,﹣b)在第_____象限,若点A、B关于y轴对称,则点P(﹣a,﹣b)在第_____象限.且平行于y轴的直线上;
②当m≠0时,点P(m2,﹣m)在第四象限;
③与点(﹣3,4)关于y轴对称的点的坐标是(﹣3,﹣4);
④在第一象限的点N到x轴的距离是1,到y轴的距离是2,则点N的坐标为(2,1).
其中正确的是( )
A.①③ B.②④ C.①④ D.②③
10.如图,在3×3的正方形网格中有四个格点A,B,C,D,以其中一个点为原点,网格线所在的直线为坐标轴,建立平面直角坐标系,使其余的三个点中有两个点关于一条坐标轴对称,则原点为( )
A.A点 B.B点 C.C点 D.D点
二.填空题
11.在平面直角坐标系中,点A(2,﹣3)与点B(a,b)关于y轴对称,则a﹣b= .
12.已知在平面直角坐标系中点A的坐标为(﹣1,0),则A点关于y轴对称的点坐标为 .
13.若点A(a,2)与B(3,b)关于x轴对称,则a﹣b= .
14.已知点M(a+3,﹣5)和N(2,b﹣1)关于x轴对称,则ab的值为 .
15.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(a,b),经过第1次变换后所得的A1坐标是(a,﹣b),则经过第2020次变换后所得的点A2020坐标是 .
三.解答题
16.如图,在4×5的网格中,A,B,C均为格点(最小正方形的顶点).在图1、图2中分别画一个与△ABC成轴对称的格点三角形,所画的两个三角形的位置不同.
17.如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上,如果用(1,0)表示C点的位置,用(4,1)表示B点的位置.
(1)画出直角坐标系xOy,写出点A的坐标;
(2)作出△ABC关于x轴对称的△A′B′C′,并直接写出点A′,B′的坐标.
18.△ABC在平面直角坐标系xOy中的位置如图所示.
(1)画出△ABC关于y轴对称的△A1B1C1,并写出各顶点坐标;
(2)在(1)的基础上,将△A1B1C1先向右平移3个单位,再向下平移2个单位得△A2B2C2,作出△A2B2C2,直接写出点(,﹣)与△A2B2C2的位置关系.
19.如图,△ABC的三个顶点坐标分别为A(0,0),B(4,﹣2),C(5,3),将三角形三个顶点的坐标作如下变化:
(1)画出△ABC关于x轴对称的图形;
(2)求△ABC的面积.
参考答案与试题解析
一.选择题
1.【解答】解:∵点A(m,n)和点B(5,﹣7)关于x轴对称,
∴m=5,n=7,
故选:A.
2.【解答】解:∵点A(﹣2a,6)与B(4,b+2)关于x轴对称,
∴﹣2a=4,b+2=﹣6,
解得:a=﹣2,b=﹣8,
故选:D.
3.【解答】解:点(3,2)关于x轴的对称点为:(3,﹣2).
故选:B.
4.【解答】解:∵将点P(2,1)向右平移3个单位得到点P1,
∴点P1的坐标是(5,1),
∴点P1关于x轴的对称点P2的坐标是(5,﹣1).
故选:B.
5.【解答】解:(2,b+2)与点(a﹣3,﹣1)关于x轴对称,得
a﹣3=2,b+2=1.
解得a=5,b=﹣1,
故选:D.
6.【解答】解:∵点A(m+2,﹣3),B(﹣2,n﹣4)关于y轴对称,
∴m+2=2,n﹣4=﹣3,
解得:m=0,n=1,
则m﹣n=﹣1.
故选:C.
7.【解答】解:∵顶点B的坐标是(﹣5,2),将其向右平移3个单位得到顶点B1,
∴顶点B1的坐标为(﹣2,2).
又∵顶点B2和顶点B1关于y轴对称,
∴顶点B2的坐标为(2,2).
故选:C.
8.【解答】解:∵点A(a,3),B(﹣3,b)关于x轴对称,
∴a=﹣3,b=﹣3,
∴﹣a>0,﹣b>0,
∴点P(﹣a,﹣b)在第一象限,
∵点A(a,3),B(﹣3,b)关于y轴对称,
∴a=3,b=3,
∴﹣a<0,﹣b<0,
∴点P(﹣a,﹣b)在第三象限,
故选:A.
9.【解答】解:①横坐标为﹣3的点在经过点(﹣3,0)且平行于y轴的直线上,故正确;
②当m≠0时,点P(m2,﹣m)在第四象限或第一象限,故错误;
③与点(﹣3,4)关于y轴对称的点的坐标是(3,4),故错误;
④在第一象限的点N到x轴的距离是1,到y轴的距离是2,则点N的坐标为(2,1),故正确.
故选:C.
10.【解答】解:如图所示:
以B点为原点,建立平面直角坐标系,此时存在两个点A,C关于x轴对称,
故选:B.
二.填空题(共5小题)
11.【解答】解:∵点A(2,﹣3)与点B(a,b)关于y轴对称,
∴a=﹣2,b=﹣3,
∴a﹣b=﹣2+3=1.
故答案为:1.
12.【解答】解:∵平面直角坐标系中点A的坐标为(﹣1,0),
∴A点关于y轴对称的点坐标为(1,0),
故答案为:(1,0).
13.【解答】解:∵点A(a,2)与点B(3,b)关于x轴对称,
∴a=3,b=﹣2,
∴a﹣b=3﹣(﹣2)=3+2=5,
故答案为:5.
14.【解答】解:∵点M(a+3,﹣5)和N(2,b﹣1)关于x轴对称,
∴a+3=2,b﹣1=5.
解得a=﹣1,b=6,
∴ab=(﹣1)6=1,
故答案为:1.
15.【解答】解:点A第一次关于x轴对称后在第四象限,
点A第二次关于y轴对称后在第三象限,
点A第三次关于x轴对称后在第二象限,
点A第四次关于y轴对称后在第一象限,
即点A回到原始位置,
所以,每四次对称为一个循环组依次循环,
∵2020÷4=505,
∴经过第2020次变换后所得的A点与第一次变换的位置相同,在第四象限,
坐标为(a,﹣b).
故答案为(a,﹣b).
三.解答题(共4小题)
16.【解答】解:如图所示:△ABD即为所求.
.
17.【解答】解:(1)如图所示:A(0,2);
(2)如图所示:△A′B′C′即为所求,
A′(0,﹣2),B′(4,﹣1).
18.【解答】解:(1)如图所示:△A1B1C1即为所求,
A1(2,3),B1(1,1),C1(0,2);
(2)如图所示:△A2B2C2即为所求,
点(,﹣)是所在小正方形对角线交点,正好在△A2B2C2的边C2B2上.
19.【解答】解:(1)如图所示
