冀教版数学五年级下册5.5 土石方问题 课件(22张ppt)
文档属性
| 名称 | 冀教版数学五年级下册5.5 土石方问题 课件(22张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 09:13:36 | ||
图片预览




文档简介
第5课时 土石方问题
长方体和正方体的体积
1、结合具体事例,经历用已有知识解决土石方计算问题的过程。
2、了解“方”的含义,能够灵活运用体积计算公式解决现实生活中的实际问题。
3、在解决现实问题的过程中,感受数学在生活中的广泛应用。培养解决实际问题的能力。
【重点】灵活运用长方体和正方体的体积公式解决生活中的 实际问题。
【难点】理解计算拦河坝土石方的方法。
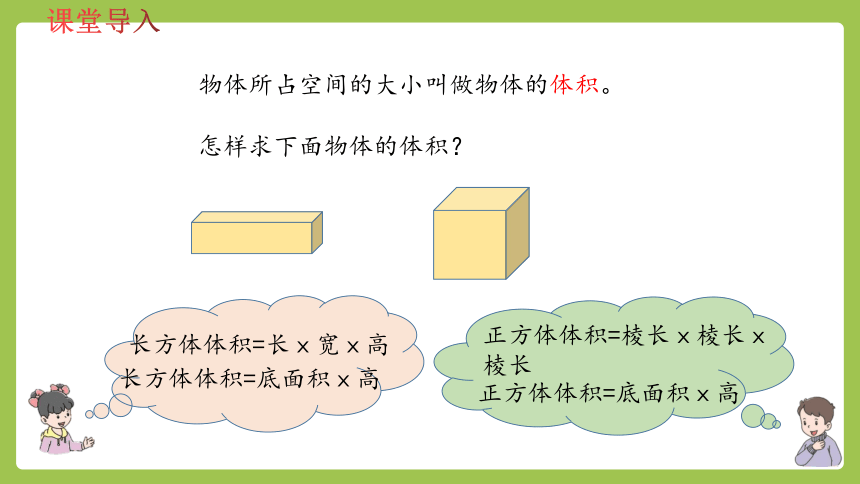
物体所占空间的大小叫做物体的体积。
怎样求下面物体的体积?
长方体体积=长ⅹ宽ⅹ高
正方体体积=棱长ⅹ棱长ⅹ棱长
长方体体积=底面积ⅹ高
正方体体积=底面积ⅹ高
土、沙、石等也用立方米作单位来计量体积。
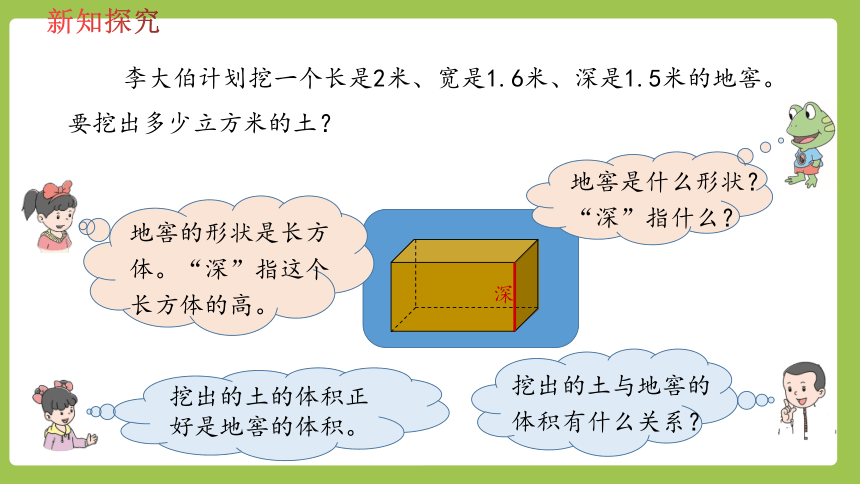
地窖是什么形状?“深”指什么?
地窖的形状是长方体。“深”指这个长方体的高。
挖出的土与地窖的体积有什么关系?
李大伯计划挖一个长是2米、宽是1.6米、深是1.5米的地窖。要挖出多少立方米的土?
挖出的土的体积正好是地窖的体积。
深
2×1.6×1.5=4.8(立方米)
生活中,计量沙、土、石子等的体积时,常常把“立方米”简称为“方”。
长方体体积=长ⅹ宽ⅹ高
答:要挖出4.8立方米的土。
李大伯计划挖一个长是2米、宽是1.6米、深是1.5米的地窖。要挖出多少立方米的土?
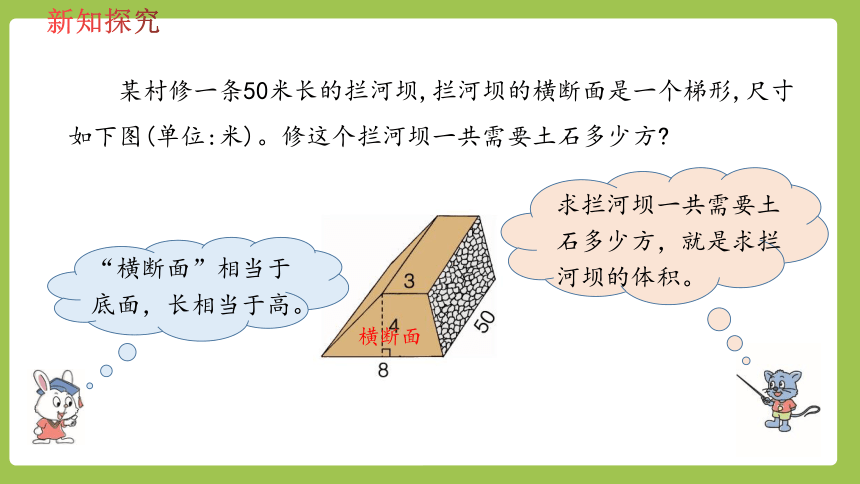
求拦河坝一共需要土石多少方,就是求拦河坝的体积。
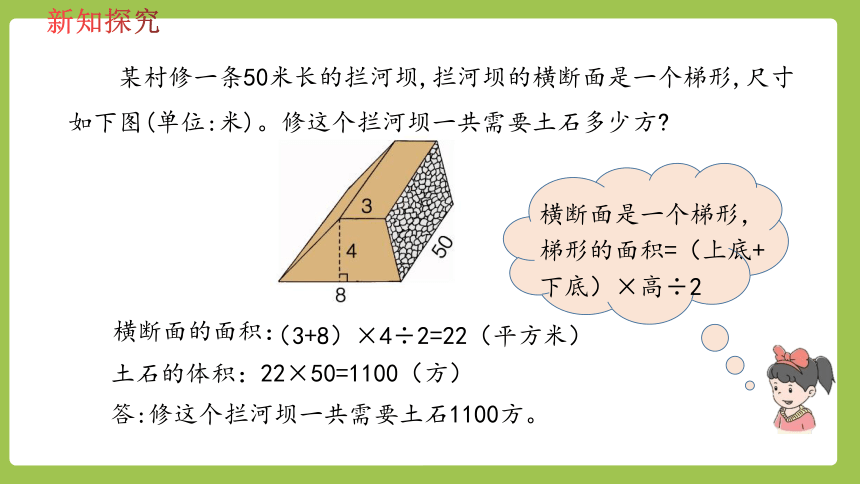
某村修一条50米长的拦河坝,拦河坝的横断面是一个梯形,尺寸如下图(单位:米)。修这个拦河坝一共需要土石多少方?
“横断面”相当于底面,长相当于高。
横断面
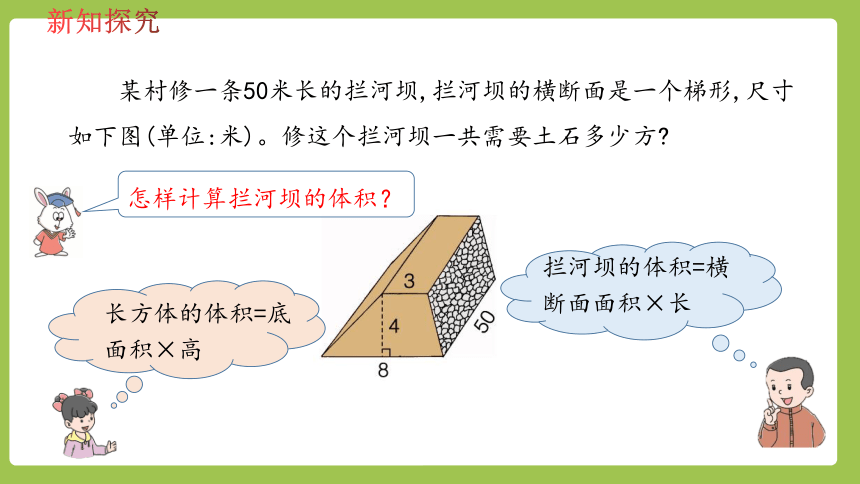
怎样计算拦河坝的体积?
拦河坝的体积=横断面面积×长
长方体的体积=底面积×高
某村修一条50米长的拦河坝,拦河坝的横断面是一个梯形,尺寸如下图(单位:米)。修这个拦河坝一共需要土石多少方?
答:修这个拦河坝一共需要土石1100方。
横断面的面积:
土石的体积:
(3+8)×4÷2=22(平方米)
22×50=1100(方)
横断面是一个梯形,梯形的面积=(上底+下底)×高÷2
某村修一条50米长的拦河坝,拦河坝的横断面是一个梯形,尺寸如下图(单位:米)。修这个拦河坝一共需要土石多少方?
某地有一段古墙,墙由长方体砖砌成,尺寸如下图。
你得到了哪些数学信息?
一块砖的长、宽、高分别是50cm、25cm、20cm。
古墙的长、宽、高分别是6m、0.5m、4m,它是个不完整的长方体;缺口的长、宽、高分别是2m、0.5m、2m。
50×25×20
=1250×20
=25000(cm3)
求一块砖的体积。
长方体体积=长ⅹ宽ⅹ高
先把墙看作完整的长方体求出体积:
2+2=4(m)
6×0.5×4=12(m3)
求这段古墙的体积。
再求出缺口处的体积:
2×0.5×2=2(m3)
最后求这段墙的体积:
12-2=10(m3)
方法一:先把墙看作完整的长方体求出体积,再减去缺口的体积。
先求出小长方体体积:
2×0.5×2=2(m3)
求这段古墙的体积。
方法二:把墙看作两个长方体的组合。
再求出大长方体的体积:
6-2=4(m) 4×0.5×4=8(m3)
最后求出这段墙的体积:
2+8=10(m3)
大长方体
小长方体
10m3 =10000000cm3
答:这段古墙至少有400块这样的方砖。
10000000÷25000=400(块)
这段古墙至少有多少块这样的方砖?
古墙体积÷一块方砖的体积=最少块数
铁路轨枕的体积=横断面面积×长
记得要统一单位哦!
下面是一根混凝土的铁路轨枕,求它的体积。
横断面的面积:
铁路轨枕的体积:
(16+28)×16÷2=352(m2)
352×180=63360(cm3)
1.8m=180cm
下面是一根混凝土的铁路轨枕,求它的体积。
横断面的面积:
铁路轨枕的体积:
(1.6+2.8)×1.6÷2=3.52(dm2)
3.52×18=63.36(dm3)
16cm=1.6dm
28cm=2.8dm
1.8m=18dm
用分米作单位。
下面是一根混凝土的铁路轨枕,求它的体积。
横断面的面积:
铁路轨枕的体积:
(0.16+0.28)×0.16÷2=0.0352(m2)
0.0352×1.8=0.06336(m3)
16cm=0.16m
28cm=0.28m
用米作单位。
用长方体体积减去小正方体的体积。
这个图形可以看作是从一个长方体中挖掉一个正方体。
计算下面物体的体积。(单位:厘米)
20×6×12=1440(立方厘米)
6×6×6=216(立方厘米)
1440-216=1224(立方厘米)
这个物体的体积就是两个长方体体积之和。
右图是由两个长方体木块粘成的物体,求这个物体的体积和表面积。(单位:厘米)
6×4×3=72(立方厘米)
12×6×4=288(立方厘米)
72+288=360(立方厘米)
这个物体的表面积就是两个长方体表面积之和吗?
上面小正方体的底面压住了下面长方体上面的一部分。要用两个长方体表面积之和减去小长方体的两个底面积。
(12×6+12×4+6×4)×2=288(平方厘米)
(3×6+3×4+6×4)×2=108(平方厘米)
288+108-4×6×2=348(平方厘米)
右图是由两个长方体木块粘成的物体,求这个物体的体积和表面积。(单位:厘米)
用公式V=Sh可以求横断面是梯形、三角形等形状的物体的体积。
在解决实际问题时,计量沙、土、石子等的体积时,常把“立方米”简称为“方”。
土石方问题
练一练第2、3题
长方体和正方体的体积
1、结合具体事例,经历用已有知识解决土石方计算问题的过程。
2、了解“方”的含义,能够灵活运用体积计算公式解决现实生活中的实际问题。
3、在解决现实问题的过程中,感受数学在生活中的广泛应用。培养解决实际问题的能力。
【重点】灵活运用长方体和正方体的体积公式解决生活中的 实际问题。
【难点】理解计算拦河坝土石方的方法。
物体所占空间的大小叫做物体的体积。
怎样求下面物体的体积?
长方体体积=长ⅹ宽ⅹ高
正方体体积=棱长ⅹ棱长ⅹ棱长
长方体体积=底面积ⅹ高
正方体体积=底面积ⅹ高
土、沙、石等也用立方米作单位来计量体积。
地窖是什么形状?“深”指什么?
地窖的形状是长方体。“深”指这个长方体的高。
挖出的土与地窖的体积有什么关系?
李大伯计划挖一个长是2米、宽是1.6米、深是1.5米的地窖。要挖出多少立方米的土?
挖出的土的体积正好是地窖的体积。
深
2×1.6×1.5=4.8(立方米)
生活中,计量沙、土、石子等的体积时,常常把“立方米”简称为“方”。
长方体体积=长ⅹ宽ⅹ高
答:要挖出4.8立方米的土。
李大伯计划挖一个长是2米、宽是1.6米、深是1.5米的地窖。要挖出多少立方米的土?
求拦河坝一共需要土石多少方,就是求拦河坝的体积。
某村修一条50米长的拦河坝,拦河坝的横断面是一个梯形,尺寸如下图(单位:米)。修这个拦河坝一共需要土石多少方?
“横断面”相当于底面,长相当于高。
横断面
怎样计算拦河坝的体积?
拦河坝的体积=横断面面积×长
长方体的体积=底面积×高
某村修一条50米长的拦河坝,拦河坝的横断面是一个梯形,尺寸如下图(单位:米)。修这个拦河坝一共需要土石多少方?
答:修这个拦河坝一共需要土石1100方。
横断面的面积:
土石的体积:
(3+8)×4÷2=22(平方米)
22×50=1100(方)
横断面是一个梯形,梯形的面积=(上底+下底)×高÷2
某村修一条50米长的拦河坝,拦河坝的横断面是一个梯形,尺寸如下图(单位:米)。修这个拦河坝一共需要土石多少方?
某地有一段古墙,墙由长方体砖砌成,尺寸如下图。
你得到了哪些数学信息?
一块砖的长、宽、高分别是50cm、25cm、20cm。
古墙的长、宽、高分别是6m、0.5m、4m,它是个不完整的长方体;缺口的长、宽、高分别是2m、0.5m、2m。
50×25×20
=1250×20
=25000(cm3)
求一块砖的体积。
长方体体积=长ⅹ宽ⅹ高
先把墙看作完整的长方体求出体积:
2+2=4(m)
6×0.5×4=12(m3)
求这段古墙的体积。
再求出缺口处的体积:
2×0.5×2=2(m3)
最后求这段墙的体积:
12-2=10(m3)
方法一:先把墙看作完整的长方体求出体积,再减去缺口的体积。
先求出小长方体体积:
2×0.5×2=2(m3)
求这段古墙的体积。
方法二:把墙看作两个长方体的组合。
再求出大长方体的体积:
6-2=4(m) 4×0.5×4=8(m3)
最后求出这段墙的体积:
2+8=10(m3)
大长方体
小长方体
10m3 =10000000cm3
答:这段古墙至少有400块这样的方砖。
10000000÷25000=400(块)
这段古墙至少有多少块这样的方砖?
古墙体积÷一块方砖的体积=最少块数
铁路轨枕的体积=横断面面积×长
记得要统一单位哦!
下面是一根混凝土的铁路轨枕,求它的体积。
横断面的面积:
铁路轨枕的体积:
(16+28)×16÷2=352(m2)
352×180=63360(cm3)
1.8m=180cm
下面是一根混凝土的铁路轨枕,求它的体积。
横断面的面积:
铁路轨枕的体积:
(1.6+2.8)×1.6÷2=3.52(dm2)
3.52×18=63.36(dm3)
16cm=1.6dm
28cm=2.8dm
1.8m=18dm
用分米作单位。
下面是一根混凝土的铁路轨枕,求它的体积。
横断面的面积:
铁路轨枕的体积:
(0.16+0.28)×0.16÷2=0.0352(m2)
0.0352×1.8=0.06336(m3)
16cm=0.16m
28cm=0.28m
用米作单位。
用长方体体积减去小正方体的体积。
这个图形可以看作是从一个长方体中挖掉一个正方体。
计算下面物体的体积。(单位:厘米)
20×6×12=1440(立方厘米)
6×6×6=216(立方厘米)
1440-216=1224(立方厘米)
这个物体的体积就是两个长方体体积之和。
右图是由两个长方体木块粘成的物体,求这个物体的体积和表面积。(单位:厘米)
6×4×3=72(立方厘米)
12×6×4=288(立方厘米)
72+288=360(立方厘米)
这个物体的表面积就是两个长方体表面积之和吗?
上面小正方体的底面压住了下面长方体上面的一部分。要用两个长方体表面积之和减去小长方体的两个底面积。
(12×6+12×4+6×4)×2=288(平方厘米)
(3×6+3×4+6×4)×2=108(平方厘米)
288+108-4×6×2=348(平方厘米)
右图是由两个长方体木块粘成的物体,求这个物体的体积和表面积。(单位:厘米)
用公式V=Sh可以求横断面是梯形、三角形等形状的物体的体积。
在解决实际问题时,计量沙、土、石子等的体积时,常把“立方米”简称为“方”。
土石方问题
练一练第2、3题
