冀教版数学四年级下册整理与评价- 用字母表示数 三位数乘两位数 课件(24张ppt)
文档属性
| 名称 | 冀教版数学四年级下册整理与评价- 用字母表示数 三位数乘两位数 课件(24张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 00:00:00 | ||
图片预览





文档简介
整理与评价
第1课时 用字母表示数 三位数乘两位数
冀教版 数学 四年级 下册
1、会用含有字母的式子表示数量关系、计算公式、运算定律,能够正确理解含有字母的式子表示的含义。
2、掌握三位数乘两位数的计算方法。
3、能够运用运算定律进行简算。
4、掌握单价、数量、总价,速度、时间、路程之间的数量关系,能够解决数学问题。
同学们,本学期已经接近尾声,我们已经学完本册课本的所有知识,从今天开始我们将分类对这些知识进行梳理及巩固练习,请同学们认真回忆学过的用字母表示数和三位数乘两位数的知识,选择自己喜欢的方式进行整理。
请同学们先自己在练习本上采用自己喜欢的方式进行这单元知识的梳理。
我们先来整理用字母表示数这一部分的知识。
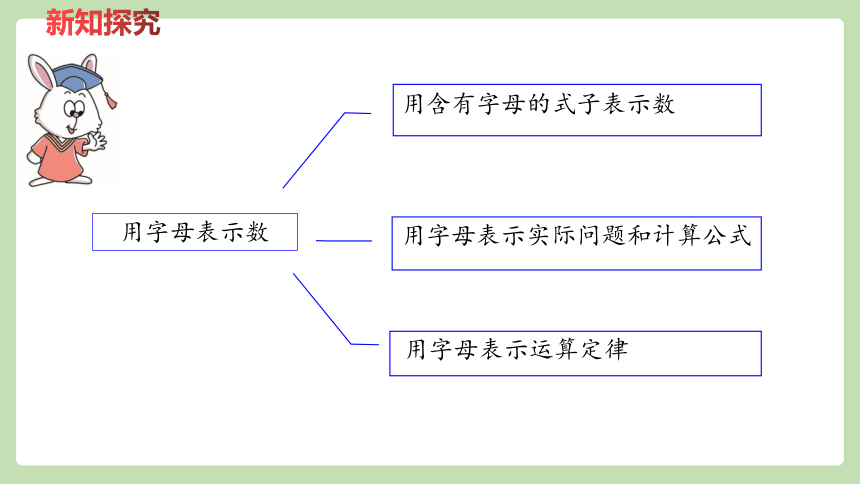
用字母表示数
用含有字母的式子表示数
用字母表示实际问题和计算公式
用字母表示运算定律
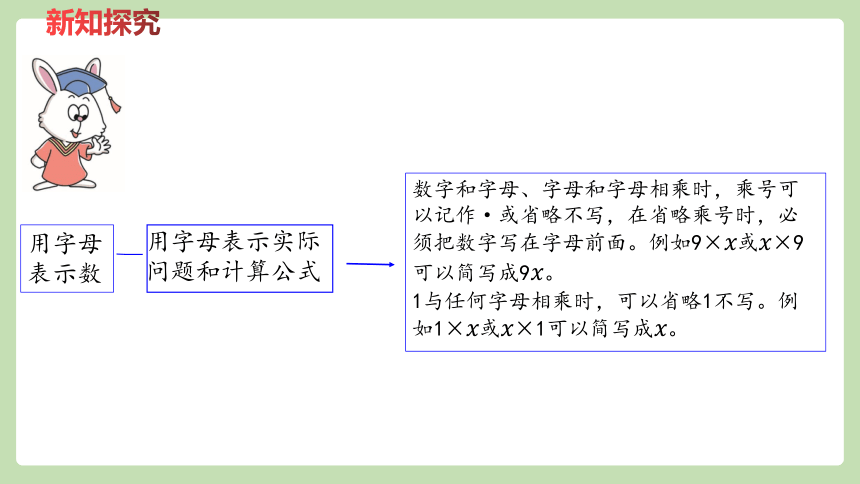
数字和字母、字母和字母相乘时,乘号可以记作·或省略不写,在省略乘号时,必须把数字写在字母前面。例如9×????或????×9可以简写成9????。
1与任何字母相乘时,可以省略1不写。例如1×????或????×1可以简写成????。
?
用字母表示数
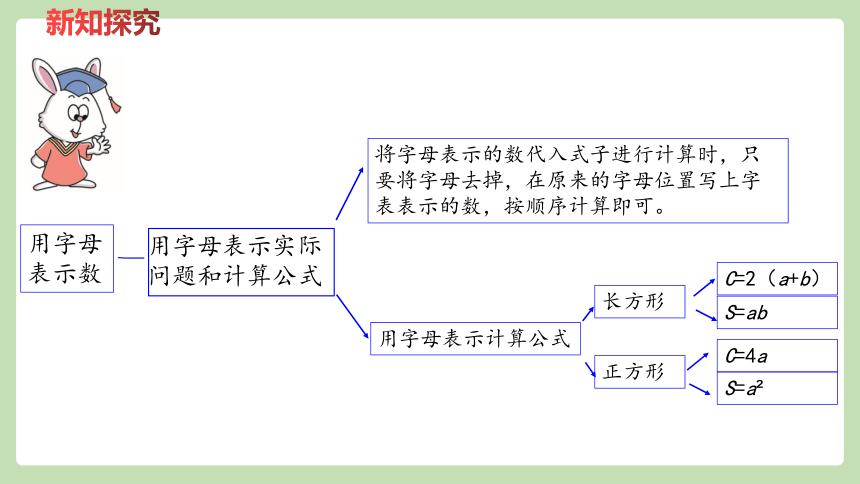
用字母表示实际问题和计算公式
用字母表示数
用字母表示计算公式
用字母表示实际问题和计算公式
长方形
正方形
C=2(a+b)
S=ab
C=4a
S=a?
将字母表示的数代入式子进行计算时,只要将字母去掉,在原来的字母位置写上字表表示的数,按顺序计算即可。
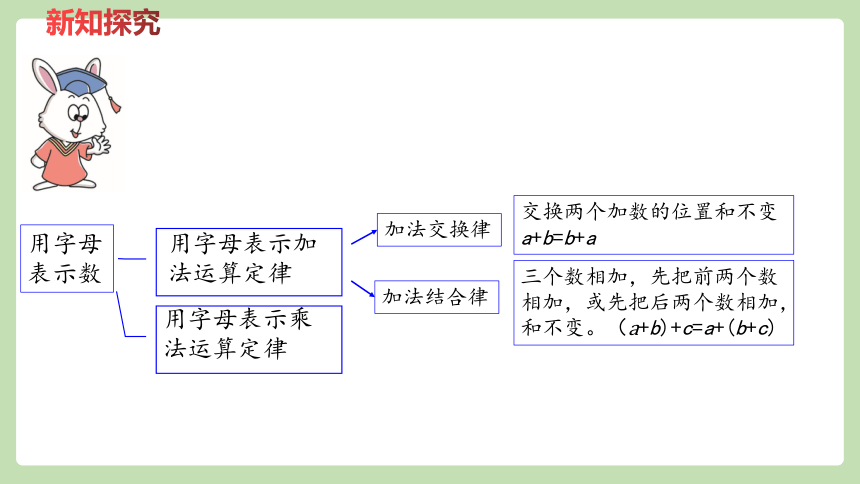
用字母表示数
加法交换律
用字母表示加法运算定律
加法结合律
交换两个加数的位置和不变a+b=b+a
三个数相加,先把前两个数相加,或先把后两个数相加,和不变。(a+b)+c=a+(b+c)
用字母表示乘法运算定律
请同学们先自己在练习本上采用自己喜欢的方式进行本单元知识的梳理。
接下来整理三位数乘两位数这一部分的知识
三位数乘两位数
乘法计算
数量关系
乘法运算定律
三位数乘两位数
乘法计算
笔算三位数乘两位数
积的变化规律
乘法估算
先用两位数的个位上的数去乘三位数,得数的末位和个位对齐,再用两位数的十位上的数去乘三位数,得数的末位和十位对齐,然后把两次乘得的积加起来。
在乘法算式里,一个因数不变,另一个因数乘一个数或除以一个不为0的数,积也乘或除以相同的数。
一般情况,估算时是根据“四舍五入”法把数据估成整十、整百的数,方便计算。
乘法估算,有时候应估大些,有时候应估小些,应根据实际情况而定,不能机械地采用“四舍五入”法取近似数,但是结果一定要接近准确值。
三位数乘两位数
数量关系
单价
数量
总价
速度时间路程
单价×数量=总价
总价÷数量=单价
总价÷单价=数量
速度×时间=路程
路程÷速度=时间
路程÷时间=速度
三位数乘两位数
乘法运算定律
乘法交换律
乘法分配律
两个因数相乘,交换因数的位置,积不变。
用字母表示为a×b=b×a
两个数的和乘一个数,等于两个加数分别乘这个数,再相加。
用字母表示为
(a+b)×c=a×c+b×c
乘法结合律
三个数相乘,先乘前两个数或先乘后两个数,积不变。
用字母表示为
(a×b)×c=a×(b×c)
考考你。
1.说出下面每个式子所表示的意思。
(1)东方小学四年级有女生45名,男生比女生多????名。
45+???? 45+????+45
(2)一本书有a页,王丽每天看10页,看了b天。
10b a-10b a÷10
?
1
2
1
2
3
先思考每个字母表示的意思,再思考每个式子表示的意思。
考考你。
1.说出下面每个式子所表示的意思。
(1)东方小学四年级有女生45名,男生比女生多????名。
45+???? 45+????+45
(2)一本书有a页,王丽每天看10页,看了b天。
10b a-10b a÷10
?
1
2
1
2
3
45+????表示东方小学四年级男生的人数。
45+????+45表示东方小学四年级的总人数。
?
10b表示王丽b天看的页数。
a-10b 表示还剩的页数。
a÷10表示王丽看这本书用的天数。
速度×时间=路程
路程÷速度=时间
考考你。
2.填表。说一说用到什么数量关系。
用到速度、时间、路程三个数量关系。
{BC89EF96-8CEA-46FF-86C4-4CE0E7609802}行车时间(时)
行驶路程(千米)
2
450
9
t
90千米/时
考考你。
2.填表。说一说用到什么数量关系。
{BC89EF96-8CEA-46FF-86C4-4CE0E7609802}行车时间(时)
行驶路程(千米)
2
450
9
t
90×2=180
450÷90=5
180
5
810
90t
90×9=810
90×t =90t
90千米/时
考考你。
3.下面的算式各表示哪个运算定律?举例说明。
(a×b)×c=a×(b×c)
a+b=b+a
(a+b)+c=a+(b+c)
(a+b)×c=a×c+b×c
a×b=b×a
乘法结合律 例:(125×25)×4=125×(25×4)
加法交换律 例:138+62=62+138
加法结合律 例:(175+36)+64=175+(36+64)
乘法分配律 例:(100+2)×98=100×98+2×98
乘法交换律 例:125×8=8×125
考考你。
4.怎样算简便就怎样算。
246+98 198×34 15×4×25×6
95×102 126×8+74×8 265+158+42+35
先分析符合哪种运算定律,再进行简算。
考考你。
4.怎样算简便就怎样算。
246+98 198×34 15×4×25×6
98接近100,将98分解成100-2。
=246+100-2
=346-2
=344
198接近200,将198分解成200-2,再运用乘法分配律。
=(200-2)×34
=200×34-2×34
=6800-68
=6732
运用乘法结合律,将15和6结合,4和25结合。
=15×6×4×25
=(15×6)×(4×25)
=90×100
=9000
考考你。
4.怎样算简便就怎样算。
95×102 126×8+74×8 265+158+42+35
=95×(100+2)
=95×100+95×2
=9500+190
=9690
运用乘法分配律。
=(126+74)×8
=200×8
=1600
运用加法结合律,将265和35结合,158和42结合。
=265+35+158+42
=(265+35)+(158+42)
=300+200
=500
将102分解成100+2,再运用乘法分配律。
考考你。
5.用计算器计算。
125×16=
125×8×2=
比较两个算式的因数和积,你发现了什么?
2000
2000
这两个算式的乘积是相等的,第二个算式中的后两个因数是将第一个算式中的第二个因数16分解成(8×2)得到的。
125×16
=125×8×2
=1000×2
=2000
计算125×16时可以这样算简便。
能够正确理解含有字母的式子表示的意义,会运用数量关系式解决生活中的实际问题,能够运用运算定律进行简便运算。
整理与评价1
完成相关练习
第1课时 用字母表示数 三位数乘两位数
冀教版 数学 四年级 下册
1、会用含有字母的式子表示数量关系、计算公式、运算定律,能够正确理解含有字母的式子表示的含义。
2、掌握三位数乘两位数的计算方法。
3、能够运用运算定律进行简算。
4、掌握单价、数量、总价,速度、时间、路程之间的数量关系,能够解决数学问题。
同学们,本学期已经接近尾声,我们已经学完本册课本的所有知识,从今天开始我们将分类对这些知识进行梳理及巩固练习,请同学们认真回忆学过的用字母表示数和三位数乘两位数的知识,选择自己喜欢的方式进行整理。
请同学们先自己在练习本上采用自己喜欢的方式进行这单元知识的梳理。
我们先来整理用字母表示数这一部分的知识。
用字母表示数
用含有字母的式子表示数
用字母表示实际问题和计算公式
用字母表示运算定律
数字和字母、字母和字母相乘时,乘号可以记作·或省略不写,在省略乘号时,必须把数字写在字母前面。例如9×????或????×9可以简写成9????。
1与任何字母相乘时,可以省略1不写。例如1×????或????×1可以简写成????。
?
用字母表示数
用字母表示实际问题和计算公式
用字母表示数
用字母表示计算公式
用字母表示实际问题和计算公式
长方形
正方形
C=2(a+b)
S=ab
C=4a
S=a?
将字母表示的数代入式子进行计算时,只要将字母去掉,在原来的字母位置写上字表表示的数,按顺序计算即可。
用字母表示数
加法交换律
用字母表示加法运算定律
加法结合律
交换两个加数的位置和不变a+b=b+a
三个数相加,先把前两个数相加,或先把后两个数相加,和不变。(a+b)+c=a+(b+c)
用字母表示乘法运算定律
请同学们先自己在练习本上采用自己喜欢的方式进行本单元知识的梳理。
接下来整理三位数乘两位数这一部分的知识
三位数乘两位数
乘法计算
数量关系
乘法运算定律
三位数乘两位数
乘法计算
笔算三位数乘两位数
积的变化规律
乘法估算
先用两位数的个位上的数去乘三位数,得数的末位和个位对齐,再用两位数的十位上的数去乘三位数,得数的末位和十位对齐,然后把两次乘得的积加起来。
在乘法算式里,一个因数不变,另一个因数乘一个数或除以一个不为0的数,积也乘或除以相同的数。
一般情况,估算时是根据“四舍五入”法把数据估成整十、整百的数,方便计算。
乘法估算,有时候应估大些,有时候应估小些,应根据实际情况而定,不能机械地采用“四舍五入”法取近似数,但是结果一定要接近准确值。
三位数乘两位数
数量关系
单价
数量
总价
速度时间路程
单价×数量=总价
总价÷数量=单价
总价÷单价=数量
速度×时间=路程
路程÷速度=时间
路程÷时间=速度
三位数乘两位数
乘法运算定律
乘法交换律
乘法分配律
两个因数相乘,交换因数的位置,积不变。
用字母表示为a×b=b×a
两个数的和乘一个数,等于两个加数分别乘这个数,再相加。
用字母表示为
(a+b)×c=a×c+b×c
乘法结合律
三个数相乘,先乘前两个数或先乘后两个数,积不变。
用字母表示为
(a×b)×c=a×(b×c)
考考你。
1.说出下面每个式子所表示的意思。
(1)东方小学四年级有女生45名,男生比女生多????名。
45+???? 45+????+45
(2)一本书有a页,王丽每天看10页,看了b天。
10b a-10b a÷10
?
1
2
1
2
3
先思考每个字母表示的意思,再思考每个式子表示的意思。
考考你。
1.说出下面每个式子所表示的意思。
(1)东方小学四年级有女生45名,男生比女生多????名。
45+???? 45+????+45
(2)一本书有a页,王丽每天看10页,看了b天。
10b a-10b a÷10
?
1
2
1
2
3
45+????表示东方小学四年级男生的人数。
45+????+45表示东方小学四年级的总人数。
?
10b表示王丽b天看的页数。
a-10b 表示还剩的页数。
a÷10表示王丽看这本书用的天数。
速度×时间=路程
路程÷速度=时间
考考你。
2.填表。说一说用到什么数量关系。
用到速度、时间、路程三个数量关系。
{BC89EF96-8CEA-46FF-86C4-4CE0E7609802}行车时间(时)
行驶路程(千米)
2
450
9
t
90千米/时
考考你。
2.填表。说一说用到什么数量关系。
{BC89EF96-8CEA-46FF-86C4-4CE0E7609802}行车时间(时)
行驶路程(千米)
2
450
9
t
90×2=180
450÷90=5
180
5
810
90t
90×9=810
90×t =90t
90千米/时
考考你。
3.下面的算式各表示哪个运算定律?举例说明。
(a×b)×c=a×(b×c)
a+b=b+a
(a+b)+c=a+(b+c)
(a+b)×c=a×c+b×c
a×b=b×a
乘法结合律 例:(125×25)×4=125×(25×4)
加法交换律 例:138+62=62+138
加法结合律 例:(175+36)+64=175+(36+64)
乘法分配律 例:(100+2)×98=100×98+2×98
乘法交换律 例:125×8=8×125
考考你。
4.怎样算简便就怎样算。
246+98 198×34 15×4×25×6
95×102 126×8+74×8 265+158+42+35
先分析符合哪种运算定律,再进行简算。
考考你。
4.怎样算简便就怎样算。
246+98 198×34 15×4×25×6
98接近100,将98分解成100-2。
=246+100-2
=346-2
=344
198接近200,将198分解成200-2,再运用乘法分配律。
=(200-2)×34
=200×34-2×34
=6800-68
=6732
运用乘法结合律,将15和6结合,4和25结合。
=15×6×4×25
=(15×6)×(4×25)
=90×100
=9000
考考你。
4.怎样算简便就怎样算。
95×102 126×8+74×8 265+158+42+35
=95×(100+2)
=95×100+95×2
=9500+190
=9690
运用乘法分配律。
=(126+74)×8
=200×8
=1600
运用加法结合律,将265和35结合,158和42结合。
=265+35+158+42
=(265+35)+(158+42)
=300+200
=500
将102分解成100+2,再运用乘法分配律。
考考你。
5.用计算器计算。
125×16=
125×8×2=
比较两个算式的因数和积,你发现了什么?
2000
2000
这两个算式的乘积是相等的,第二个算式中的后两个因数是将第一个算式中的第二个因数16分解成(8×2)得到的。
125×16
=125×8×2
=1000×2
=2000
计算125×16时可以这样算简便。
能够正确理解含有字母的式子表示的意义,会运用数量关系式解决生活中的实际问题,能够运用运算定律进行简便运算。
整理与评价1
完成相关练习
