27.2.1 点和圆的位置关系 课件(共45张PPT)
文档属性
| 名称 | 27.2.1 点和圆的位置关系 课件(共45张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 20:18:48 | ||
图片预览





文档简介
(共45张PPT)
第二十七章
圆
27.2
与圆有关的位置关系
1.点和圆的位置关系
华东师大版
九年级数学下册
教学课件
目录
1
新课目标
新课进行时
3
2
情景导学
知识小结
4
CONTENTS
随堂演练
5
课后作业
6
新课目标
1
新课目标
【知识与技能】
1.掌握点和圆的三种位置关系
2.了解不在同一直线上的三个点确定一个圆,以及过不在同一直线上的三个点作圆的方法
【过程与方法】
经历不在同一直线上的三个点确定一个圆的探索过程,培养学生的探索能力.
【情感态度】
形成解决问题的基本策略,体验解决问题策略的多样性,发展实践能力与创新精神.
【教学重点】
掌握过不在同一条直线上的三个点作圆的方法;了解三角形的外接圆、三角形的外心等概念.
【教学难点】
经历不在同一条直线上的三个点确定一个圆的探索过程,并能过不在同一条直线上的三个点作圆.
情景导学
2
情景导学
你玩过飞镖吗?它的靶子是由一些圆组成的,你知道击中靶子上不同位置的成绩是如何计算的吗?
情境引入
想一想
新课进行时
3
新课进行时
核心知识点一
点和圆的位置关系
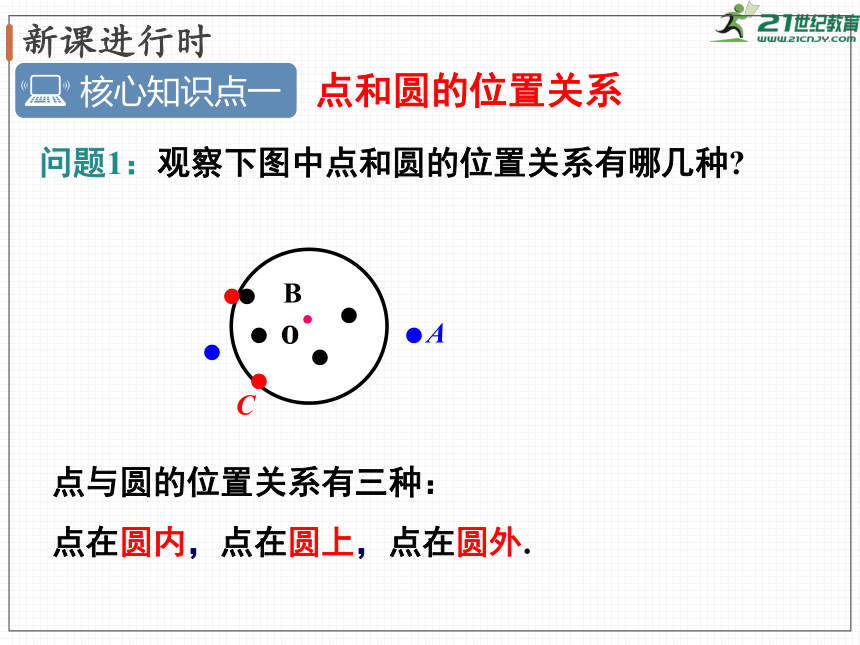
问题1:观察下图中点和圆的位置关系有哪几种?
.
o
.
C
.
.
.
.
B
.
.A
.
点与圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.
新课进行时
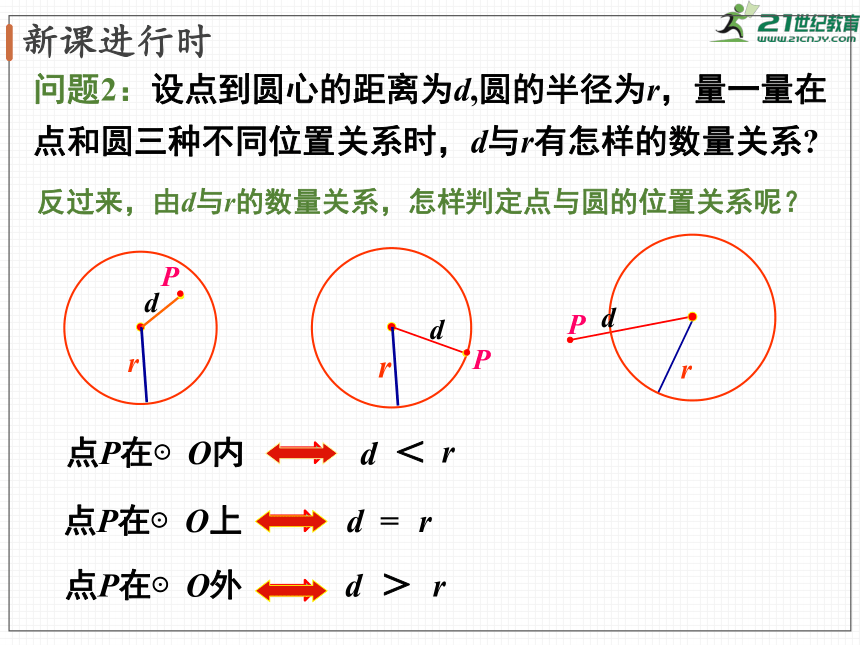
问题2:设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?
点P在⊙O内
点P在⊙O上
点P在⊙O外
d
d
d
r
P
d
P
r
d
P
r
d
<
r
r
=
>
r
反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?
新课进行时
1.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在
;点B在
;点C在
.
练一练:
圆内
圆上
圆外
2.圆心为O的两个同心圆,半径分别为1和2,若OP=
,则点P在(
)
A.大圆内
B.小圆内
C.小圆外
D.大圆内,小圆外
o
D
新课进行时
要点归纳
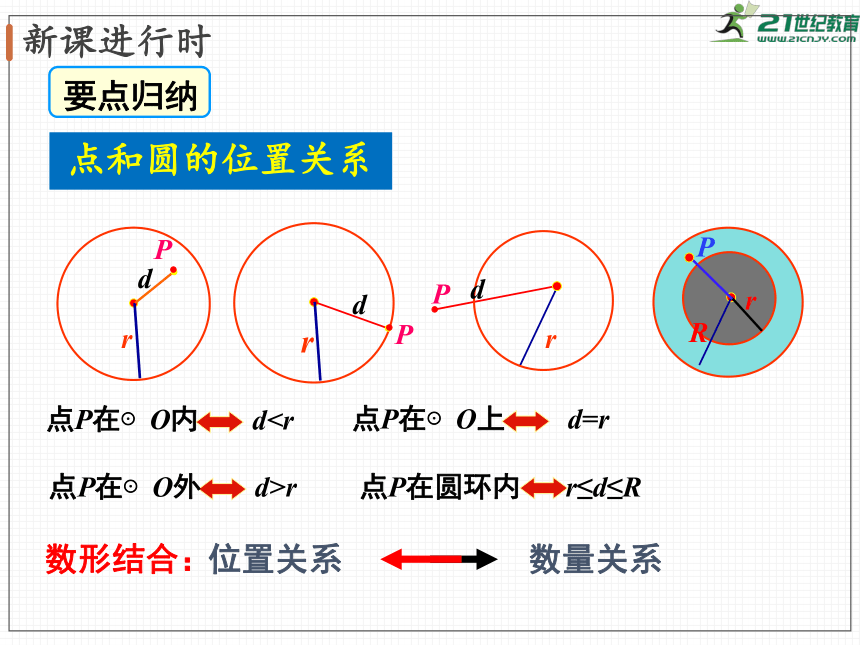
点和圆的位置关系
r
P
d
P
r
d
P
r
d
R
r
P
点P在⊙O内
d点P在⊙O上
d=r
点P在⊙O外
d>r
点P在圆环内
r≤d≤R
数形结合:
位置关系
数量关系
新课进行时
例1:如图,已知矩形ABCD的边AB=3,AD=4.
(1)以A为圆心,4为半径作⊙A,则点B、C、D与⊙A的位置关系如何?
解:AD=4=r,故D点在⊙A上
AB=3AC=5>r,故C点在⊙A外
新课进行时
(2)若以A点为圆心作⊙A,使B、C、D三点中至少有一点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围?(直接写出答案)
3新课进行时
变式:如图,在直角坐标系中,点A的坐标为(2,1),P是x轴上一点,要使△PAO为等腰三角形,满足条件的P有几个?求出点P的坐标.
新课进行时
核心知识点二
过不共线三点作圆
问题1如何过一个点A作一个圆?过点A可以作多少个圆?
合作探究
·
·
·
·
·
以不与A点重合的任意一点为圆心,以这个点到A点的距离为半径画圆即可;
可作无数个圆.
A
新课进行时
问题2如何过两点A、B作一个圆?过两点可以作多少
个圆?
·
·
·
·
A
B
作线段AB的垂直平分线,以其上任意一点为圆心,以这点和点A或B的距离为半径画圆即可;
可作无数个圆.
新课进行时
问题3:过不在同一直线上的三点能不能确定一个圆?
A
B
C
D
E
G
F
●o
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
新课进行时
有且只有
位置关系
定理:
不在同一直线上的三个点确定一个圆.
A
B
C
D
E
G
F
●o
归纳总结
新课进行时
已知:不在同一直线上的三点A、B、C.
求作:
⊙O,使它经过点A、B、C.
作法:1、连结AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆。
所以⊙O就是所求作的圆.
O
N
M
F
E
A
B
C
练一练
新课进行时
问题4:现在你知道怎样将一个如图所示的破损的圆盘复原了吗?
方法:
1、在圆弧上任取三点A、B、C;
2、作线段AB、BC的垂直平分线,其交点O即为圆心;
3、以点O为圆心,OC长为半径作圆.
⊙O即为所求.
A
B
C
O
新课进行时
某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等。请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?
●
●
●
B
A
C
针对训练
新课进行时
核心知识点三
三角形的外接圆及外心
试一试:
已知△ABC,用直尺与圆规作出过A、B、C三点的圆.
A
B
C
O
新课进行时
1.
外接圆
⊙O叫做△ABC的________,
△ABC叫做⊙O的____________.
到三角形三个顶点的距离相等.
2.三角形的外心:
定义:
●O
A
B
C
外接圆
内接三角形
三角形外接圆的圆心叫做三角形的外心.
作图:
三角形三边中垂线的交点.
性质:
要点归纳
新课进行时
判一判:
下列说法是否正确.
(1)任意的一个三角形一定有一个外接圆(
)
(2)任意一个圆有且只有一个内接三角形(
)
(3)经过三点一定可以确定一个圆(
)
(4)三角形的外心到三角形各顶点的距离相等(
)
√
×
×
√
新课进行时
画一画:分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系。
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边的中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
新课进行时
经过三角形的三个顶点的圆叫做三角形的外接圆;外接圆的圆心叫三角形的外心;三角形的外心到三角形的三个顶点的距离相等.
要点归纳
新课进行时
例2:如图,将△AOB置于平面直角坐标系中,O为原点,∠ABO=60°,若△AOB的外接圆与y轴交于点D(0,3).
(1)求∠DAO的度数;
(2)求点A的坐标和△AOB外接圆的面积.
解:(1)∵∠ADO=∠ABO=60°,
∠DOA=90°,
∴∠DAO=30°;
典例精析
新课进行时
(2)求点A的坐标和△AOB外接圆的面积.
(2)∵点D的坐标是(0,3),∴OD=3.
在直角△AOD中,
OA=OD·tan∠ADO=
,
AD=2OD=6,
∴点A的坐标是(
,0).
∵∠AOD=90°,∴AD是圆的直径,
∴△AOB外接圆的面积是9π.
方法总结:图形中求三角形外接圆的面积时,关键是确定外接圆的直径(或半径)长度.
新课进行时
例3
如图,在△ABC中,O是它的外心,BC=24cm,O到BC的距离是5cm,求△ABC的外接圆的半径。
解:连接OB,过点O作OD⊥BC.
D
则OD=5cm,
在Rt△OBD中
即△ABC的外接圆的半径为13cm.
解析:由外心的定义可知外接圆的半径等于OB,过点O作OD⊥BC,易得BD=12cm.由此可求它的外接圆的半径.
知识小结
4
知识小结
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d位置关系数量化
作圆
过一点可以作无数个圆
过两点可以作无数个圆
定理:
过不在同一直线上的三个点确定一个圆
一个三角形的外接圆是唯一的.
注意:同一直线上的三个点不能作圆
点P在圆环内
r≤d≤R
R
r
P
随堂演练
5
随堂演练
1.如图,请找出图中圆的圆心,并写出你找圆心的方法?
A
B
C
O
随堂演练
2.正方形ABCD的边长为2cm,以A为圆心2cm为半径作⊙A,则点B在⊙A
;点C在⊙A
;点D在⊙A
.
上
外
上
3.⊙O的半径r为5㎝,O为原点,点P的坐标为(3,4),则点P与⊙O的位置关系为
(
)
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.在⊙O上或⊙O外
B
随堂演练
4.判断:
(1)经过三点一定可以作圆
(
)
(2)三角形的外心就是这个三角形两边垂直平分线的交点
(
)
(3)三角形的外心到三边的距离相等
(
)
(4)等腰三角形的外心一定在这个三角形内
(
)
√
×
×
×
随堂演练
5.已知:在Rt△ABC中,∠C=90°,AC=6,BC=8,则它的外接圆半径=
.
5
6.如图,△ABC内接于⊙O,若∠OAB=20°,则∠C的度数是________.
70°
随堂演练
7.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是(
)
M
R
Q
A
B
C
P
A.点P
B.点Q
C.点R
D.点M
B
随堂演练
8.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是(
)
A.第①块
B.第④块
C.第③块
D.第②块
D
随堂演练
1
·
2cm
3cm
9.画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.
O
随堂演练
10.如图,已知
Rt△ABC
中
,
若
AC=12cm,BC=5cm,求的外接圆半径。
C
B
A
O
解:设Rt△ABC
的外接圆的外心为O,连接OC,则OA=OB=OC.
∴O是斜边AB
的中点.
∵∠C=900,AC=12cm,BC=5cm.
∴AB=13cm,OA=6.5cm.
故Rt△ABC
的外接圆半径为6.5cm.
随堂演练
能力拓展:一个8×12米的长方形草地,现要安装自动喷水装置,这种装置喷水的半径为5米,你准备安装几个?
怎样安装?
请说明理由.
课后作业
6
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
第二十七章
圆
27.2
与圆有关的位置关系
1.点和圆的位置关系
华东师大版
九年级数学下册
教学课件
目录
1
新课目标
新课进行时
3
2
情景导学
知识小结
4
CONTENTS
随堂演练
5
课后作业
6
新课目标
1
新课目标
【知识与技能】
1.掌握点和圆的三种位置关系
2.了解不在同一直线上的三个点确定一个圆,以及过不在同一直线上的三个点作圆的方法
【过程与方法】
经历不在同一直线上的三个点确定一个圆的探索过程,培养学生的探索能力.
【情感态度】
形成解决问题的基本策略,体验解决问题策略的多样性,发展实践能力与创新精神.
【教学重点】
掌握过不在同一条直线上的三个点作圆的方法;了解三角形的外接圆、三角形的外心等概念.
【教学难点】
经历不在同一条直线上的三个点确定一个圆的探索过程,并能过不在同一条直线上的三个点作圆.
情景导学
2
情景导学
你玩过飞镖吗?它的靶子是由一些圆组成的,你知道击中靶子上不同位置的成绩是如何计算的吗?
情境引入
想一想
新课进行时
3
新课进行时
核心知识点一
点和圆的位置关系
问题1:观察下图中点和圆的位置关系有哪几种?
.
o
.
C
.
.
.
.
B
.
.A
.
点与圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.
新课进行时
问题2:设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?
点P在⊙O内
点P在⊙O上
点P在⊙O外
d
d
d
r
P
d
P
r
d
P
r
d
<
r
r
=
>
r
反过来,由d与r的数量关系,怎样判定点与圆的位置关系呢?
新课进行时
1.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在
;点B在
;点C在
.
练一练:
圆内
圆上
圆外
2.圆心为O的两个同心圆,半径分别为1和2,若OP=
,则点P在(
)
A.大圆内
B.小圆内
C.小圆外
D.大圆内,小圆外
o
D
新课进行时
要点归纳
点和圆的位置关系
r
P
d
P
r
d
P
r
d
R
r
P
点P在⊙O内
d
d=r
点P在⊙O外
d>r
点P在圆环内
r≤d≤R
数形结合:
位置关系
数量关系
新课进行时
例1:如图,已知矩形ABCD的边AB=3,AD=4.
(1)以A为圆心,4为半径作⊙A,则点B、C、D与⊙A的位置关系如何?
解:AD=4=r,故D点在⊙A上
AB=3
新课进行时
(2)若以A点为圆心作⊙A,使B、C、D三点中至少有一点在圆内,且至少有一点在圆外,求⊙A的半径r的取值范围?(直接写出答案)
3
变式:如图,在直角坐标系中,点A的坐标为(2,1),P是x轴上一点,要使△PAO为等腰三角形,满足条件的P有几个?求出点P的坐标.
新课进行时
核心知识点二
过不共线三点作圆
问题1如何过一个点A作一个圆?过点A可以作多少个圆?
合作探究
·
·
·
·
·
以不与A点重合的任意一点为圆心,以这个点到A点的距离为半径画圆即可;
可作无数个圆.
A
新课进行时
问题2如何过两点A、B作一个圆?过两点可以作多少
个圆?
·
·
·
·
A
B
作线段AB的垂直平分线,以其上任意一点为圆心,以这点和点A或B的距离为半径画圆即可;
可作无数个圆.
新课进行时
问题3:过不在同一直线上的三点能不能确定一个圆?
A
B
C
D
E
G
F
●o
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
新课进行时
有且只有
位置关系
定理:
不在同一直线上的三个点确定一个圆.
A
B
C
D
E
G
F
●o
归纳总结
新课进行时
已知:不在同一直线上的三点A、B、C.
求作:
⊙O,使它经过点A、B、C.
作法:1、连结AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆。
所以⊙O就是所求作的圆.
O
N
M
F
E
A
B
C
练一练
新课进行时
问题4:现在你知道怎样将一个如图所示的破损的圆盘复原了吗?
方法:
1、在圆弧上任取三点A、B、C;
2、作线段AB、BC的垂直平分线,其交点O即为圆心;
3、以点O为圆心,OC长为半径作圆.
⊙O即为所求.
A
B
C
O
新课进行时
某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等。请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?
●
●
●
B
A
C
针对训练
新课进行时
核心知识点三
三角形的外接圆及外心
试一试:
已知△ABC,用直尺与圆规作出过A、B、C三点的圆.
A
B
C
O
新课进行时
1.
外接圆
⊙O叫做△ABC的________,
△ABC叫做⊙O的____________.
到三角形三个顶点的距离相等.
2.三角形的外心:
定义:
●O
A
B
C
外接圆
内接三角形
三角形外接圆的圆心叫做三角形的外心.
作图:
三角形三边中垂线的交点.
性质:
要点归纳
新课进行时
判一判:
下列说法是否正确.
(1)任意的一个三角形一定有一个外接圆(
)
(2)任意一个圆有且只有一个内接三角形(
)
(3)经过三点一定可以确定一个圆(
)
(4)三角形的外心到三角形各顶点的距离相等(
)
√
×
×
√
新课进行时
画一画:分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系。
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边的中点,
钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
新课进行时
经过三角形的三个顶点的圆叫做三角形的外接圆;外接圆的圆心叫三角形的外心;三角形的外心到三角形的三个顶点的距离相等.
要点归纳
新课进行时
例2:如图,将△AOB置于平面直角坐标系中,O为原点,∠ABO=60°,若△AOB的外接圆与y轴交于点D(0,3).
(1)求∠DAO的度数;
(2)求点A的坐标和△AOB外接圆的面积.
解:(1)∵∠ADO=∠ABO=60°,
∠DOA=90°,
∴∠DAO=30°;
典例精析
新课进行时
(2)求点A的坐标和△AOB外接圆的面积.
(2)∵点D的坐标是(0,3),∴OD=3.
在直角△AOD中,
OA=OD·tan∠ADO=
,
AD=2OD=6,
∴点A的坐标是(
,0).
∵∠AOD=90°,∴AD是圆的直径,
∴△AOB外接圆的面积是9π.
方法总结:图形中求三角形外接圆的面积时,关键是确定外接圆的直径(或半径)长度.
新课进行时
例3
如图,在△ABC中,O是它的外心,BC=24cm,O到BC的距离是5cm,求△ABC的外接圆的半径。
解:连接OB,过点O作OD⊥BC.
D
则OD=5cm,
在Rt△OBD中
即△ABC的外接圆的半径为13cm.
解析:由外心的定义可知外接圆的半径等于OB,过点O作OD⊥BC,易得BD=12cm.由此可求它的外接圆的半径.
知识小结
4
知识小结
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d
作圆
过一点可以作无数个圆
过两点可以作无数个圆
定理:
过不在同一直线上的三个点确定一个圆
一个三角形的外接圆是唯一的.
注意:同一直线上的三个点不能作圆
点P在圆环内
r≤d≤R
R
r
P
随堂演练
5
随堂演练
1.如图,请找出图中圆的圆心,并写出你找圆心的方法?
A
B
C
O
随堂演练
2.正方形ABCD的边长为2cm,以A为圆心2cm为半径作⊙A,则点B在⊙A
;点C在⊙A
;点D在⊙A
.
上
外
上
3.⊙O的半径r为5㎝,O为原点,点P的坐标为(3,4),则点P与⊙O的位置关系为
(
)
A.在⊙O内
B.在⊙O上
C.在⊙O外
D.在⊙O上或⊙O外
B
随堂演练
4.判断:
(1)经过三点一定可以作圆
(
)
(2)三角形的外心就是这个三角形两边垂直平分线的交点
(
)
(3)三角形的外心到三边的距离相等
(
)
(4)等腰三角形的外心一定在这个三角形内
(
)
√
×
×
×
随堂演练
5.已知:在Rt△ABC中,∠C=90°,AC=6,BC=8,则它的外接圆半径=
.
5
6.如图,△ABC内接于⊙O,若∠OAB=20°,则∠C的度数是________.
70°
随堂演练
7.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是(
)
M
R
Q
A
B
C
P
A.点P
B.点Q
C.点R
D.点M
B
随堂演练
8.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是(
)
A.第①块
B.第④块
C.第③块
D.第②块
D
随堂演练
1
·
2cm
3cm
9.画出由所有到已知点的距离大于或等于2cm并且小于或等于3cm的点组成的图形.
O
随堂演练
10.如图,已知
Rt△ABC
中
,
若
AC=12cm,BC=5cm,求的外接圆半径。
C
B
A
O
解:设Rt△ABC
的外接圆的外心为O,连接OC,则OA=OB=OC.
∴O是斜边AB
的中点.
∵∠C=900,AC=12cm,BC=5cm.
∴AB=13cm,OA=6.5cm.
故Rt△ABC
的外接圆半径为6.5cm.
随堂演练
能力拓展:一个8×12米的长方形草地,现要安装自动喷水装置,这种装置喷水的半径为5米,你准备安装几个?
怎样安装?
请说明理由.
课后作业
6
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
