冀教版数学五年级下册8.2 比赛场次问题 课件(17张ppt)
文档属性
| 名称 | 冀教版数学五年级下册8.2 比赛场次问题 课件(17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 16:30:53 | ||
图片预览





文档简介
探索乐园
第2课时 比赛场次问题
1、结合具体事例,经历探索并用不同方式表示比赛场次的过程。
2、能用连线、列表等方法解决简单的组合问题,体验解决问题方法的多样化。
3、体验数学与日常生活密切相关,认识到许多实际问题可以借助直观的方法解决,并用图或表格进行表达和交流。
【重点】能用连线、列表等方法解决简单的组合问题。
【难点】探索并用不同方式表示比赛场次的过程。
同学们,你们喜欢足球运动吗?对足球比赛的赛制你了解吗?
每一届世界杯足球赛都有32支国家队,共分成8组,先进行小组赛产生16强,在小组赛中采取循环赛的赛制(单循环赛),每两支球队之间都要进行一场比赛,不能重复进行。今天这节课我们就来学习和循环比赛有关的问题。
2010年女子足球亚洲杯在中国成都举办。中国队所在的B组共有4支球队,分别是:中国、韩国、澳大利亚和越南。每2支球队之间都要进行一场比赛。
(1)中国队在小组赛中要进行几场比赛?
中国
澳大利亚
越南
韩国
3场!
要判断中国队在小组赛中要进行几场比赛,可先写出4支球队的名称,然后以中国队为起点,分别与其他3支球队连线,有几条线就有几场比赛。
2010年女子足球亚洲杯在中国成都举办。中国队所在的B组共有4支球队,分别是:中国、韩国、澳大利亚和越南。每2支球队之间都要进行一场比赛。
(2)整个小组共赛多少场?
每支球队都赛3场,4支球队一共赛12场。
这样不对!这样算有重复,还是画图看一看吧!
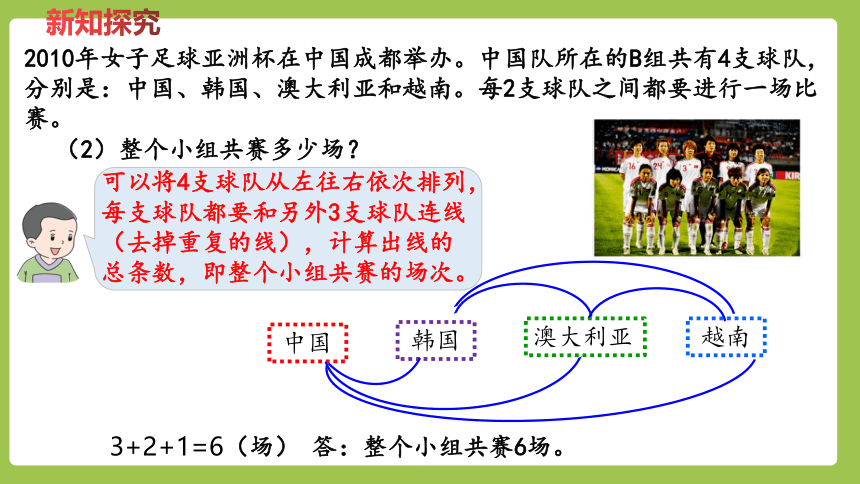
2010年女子足球亚洲杯在中国成都举办。中国队所在的B组共有4支球队,分别是:中国、韩国、澳大利亚和越南。每2支球队之间都要进行一场比赛。
(2)整个小组共赛多少场?
中国
韩国
澳大利亚
越南
3+2+1=6(场) 答:整个小组共赛6场。
可以将4支球队从左往右依次排列,每支球队都要和另外3支球队连线(去掉重复的线),计算出线的总条数,即整个小组共赛的场次。
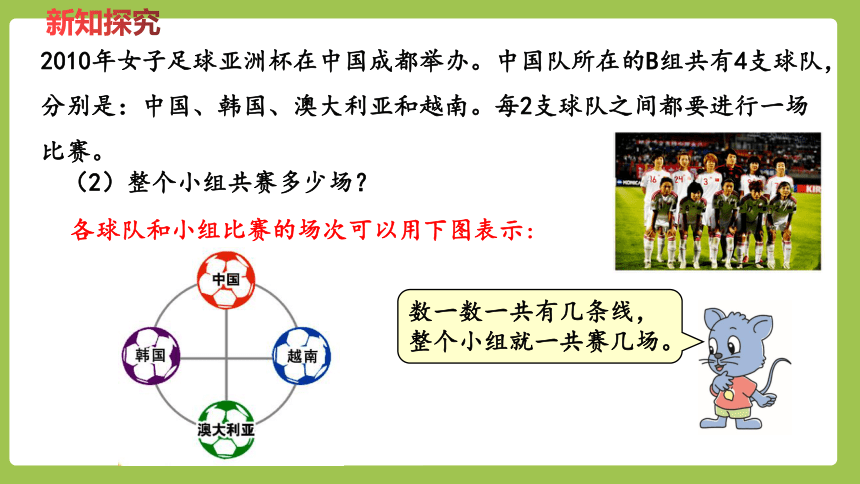
2010年女子足球亚洲杯在中国成都举办。中国队所在的B组共有4支球队,分别是:中国、韩国、澳大利亚和越南。每2支球队之间都要进行一场比赛。
(2)整个小组共赛多少场?
各球队和小组比赛的场次可以用下图表示:
数一数一共有几条线,整个小组就一共赛几场。
2010年女子足球亚洲杯在中国成都举办。中国队所在的B组共有4支球队,分别是:中国、韩国、澳大利亚和越南。每2支球队之间都要进行一场比赛。
(2)整个小组共赛多少场?
{69CF1AB2-1976-4502-BF36-3FF5EA218861}
中国 韩国 澳大利亚 越南
中、韩
中、澳
中、越
韩、澳
韩、越
澳、越
3+2+1=6(场) 口答:整个小组共赛6场。
先根据球队的支数确定所要绘制表格的行数和列数。此题中有4支球队,可以绘制(4+1)行、(4+1)列的表格(如下所示)
中国
韩国
澳大利亚
越南
一列往返于石家庄与北京的“城际”快速列车沿途只停保定一站。这列快速列车需要准备多少种火车票?
石家庄
保定
北京
2+1=3(种) 3×2=6(种)
答:这列快速列车需要准备6种火车票,即石家庄 保定,石家庄 北京,保定 北京,保定 石家庄, 北京 石家庄,北京 保定。
我用连线的方法算。
一列往返于石家庄与北京的“城际”快速列车沿途只停保定一站。这列快速列车需要准备多少种火车票?
{69CF1AB2-1976-4502-BF36-3FF5EA218861}
石家庄
保定
北京
石家庄
保定
北京
发站
到站
石家庄→保定
石家庄→北京
保定→石家庄
保定→北京
北京→石家庄
北京→保定
还可以用列表的方法。
2×3=6(种)
答:这列快速列车需要准备6种火车票,即石家庄 保定,石家庄 北京,
保定 石家庄,保定 北京, 北京 石家庄,北京 保定。
聪聪、红红、亮亮和丫丫4人进行跳棋比赛。比赛实行单循环制,每2人都要赛一局。
(1)一共比赛几局?
我用的连线的方法。
聪聪
红红
亮亮
丫丫
3+2+1=6(局)
答:一共比赛6局。
聪聪、红红、亮亮和丫丫4人进行跳棋比赛。比赛实行单循环制,每2人都要赛一局。
(1)一共比赛几局?
{69CF1AB2-1976-4502-BF36-3FF5EA218861}
聪聪
红红
亮亮
丫丫
聪聪
红红
聪聪、红红
亮亮
聪聪、亮亮
红红、亮亮
丫丫
聪聪、丫丫
红红、丫丫
亮亮、丫丫
我用的列表法。
3+2+1=6(局) 答:一共比赛6局。
聪聪、红红、亮亮和丫丫4人进行跳棋比赛。比赛实行单循环制,每2人都要赛一局。
(2)最后一局,聪聪赢了丫丫。前几局,红红、丫丫和亮亮赢的局数相同。他们各赢了几局?
聪聪赢了 局;亮亮赢了 局;
红红赢了 局;丫丫赢了 局。
他们一共比赛了6局。分别是:
红红-聪聪
红红-亮亮
红红-丫丫
亮亮-聪聪
亮亮-丫丫
聪聪-丫丫
每人都进行了三场比赛,最后一局丫丫输了,那么丫丫最多只能赢2局,如果丫丫赢2局,红红、丫丫和亮亮赢的局数相同,那么红红、亮亮也要赢2局,聪聪赢1局,合起来就是7局,超过了6局,所以丫丫只能赢1局,红红、亮亮也是每人赢1局,聪聪赢3局。
3
1
1
1
五年级一共有5个班,每个班男生各组建了一支篮球队,现在学校开展篮球比赛,五年级的这5支篮球队都要参赛。每两支篮球队之间进行一场比赛,比赛实行单循环制,一共进行几场比赛?
我用的连线的方法。
五1班
五2班
五3班
五4班
五5班
4+3+2+1=10(场) 答:一共比赛10场。
五年级一共有5个班,每个班男生各组建了一支篮球队,现在学校开展篮球比赛,五年级的这5支篮球队都要参赛。每两支篮球队之间进行一场比赛,比赛实行单循环制,一共进行几场比赛?
{69CF1AB2-1976-4502-BF36-3FF5EA218861}
五1
五2
五3
五4
五5
五1
五2
五1、五2
五3
五1、五3
五2、五3
五4
五1、五4
五2、五4
五3、五4
五5
五1、五5
五2、五5
五3、五5
五4、五5
我用的列表法。
4+3+2+1=10(场) 答:一共比赛10场。
解决简单的比赛场次问题时,要做到不重复,不遗漏。
在寻找组合方案时,可以使用连线法、列表法等方法。
比赛场次问题
(比赛场次问题)
第2课时 比赛场次问题
1、结合具体事例,经历探索并用不同方式表示比赛场次的过程。
2、能用连线、列表等方法解决简单的组合问题,体验解决问题方法的多样化。
3、体验数学与日常生活密切相关,认识到许多实际问题可以借助直观的方法解决,并用图或表格进行表达和交流。
【重点】能用连线、列表等方法解决简单的组合问题。
【难点】探索并用不同方式表示比赛场次的过程。
同学们,你们喜欢足球运动吗?对足球比赛的赛制你了解吗?
每一届世界杯足球赛都有32支国家队,共分成8组,先进行小组赛产生16强,在小组赛中采取循环赛的赛制(单循环赛),每两支球队之间都要进行一场比赛,不能重复进行。今天这节课我们就来学习和循环比赛有关的问题。
2010年女子足球亚洲杯在中国成都举办。中国队所在的B组共有4支球队,分别是:中国、韩国、澳大利亚和越南。每2支球队之间都要进行一场比赛。
(1)中国队在小组赛中要进行几场比赛?
中国
澳大利亚
越南
韩国
3场!
要判断中国队在小组赛中要进行几场比赛,可先写出4支球队的名称,然后以中国队为起点,分别与其他3支球队连线,有几条线就有几场比赛。
2010年女子足球亚洲杯在中国成都举办。中国队所在的B组共有4支球队,分别是:中国、韩国、澳大利亚和越南。每2支球队之间都要进行一场比赛。
(2)整个小组共赛多少场?
每支球队都赛3场,4支球队一共赛12场。
这样不对!这样算有重复,还是画图看一看吧!
2010年女子足球亚洲杯在中国成都举办。中国队所在的B组共有4支球队,分别是:中国、韩国、澳大利亚和越南。每2支球队之间都要进行一场比赛。
(2)整个小组共赛多少场?
中国
韩国
澳大利亚
越南
3+2+1=6(场) 答:整个小组共赛6场。
可以将4支球队从左往右依次排列,每支球队都要和另外3支球队连线(去掉重复的线),计算出线的总条数,即整个小组共赛的场次。
2010年女子足球亚洲杯在中国成都举办。中国队所在的B组共有4支球队,分别是:中国、韩国、澳大利亚和越南。每2支球队之间都要进行一场比赛。
(2)整个小组共赛多少场?
各球队和小组比赛的场次可以用下图表示:
数一数一共有几条线,整个小组就一共赛几场。
2010年女子足球亚洲杯在中国成都举办。中国队所在的B组共有4支球队,分别是:中国、韩国、澳大利亚和越南。每2支球队之间都要进行一场比赛。
(2)整个小组共赛多少场?
{69CF1AB2-1976-4502-BF36-3FF5EA218861}
中国 韩国 澳大利亚 越南
中、韩
中、澳
中、越
韩、澳
韩、越
澳、越
3+2+1=6(场) 口答:整个小组共赛6场。
先根据球队的支数确定所要绘制表格的行数和列数。此题中有4支球队,可以绘制(4+1)行、(4+1)列的表格(如下所示)
中国
韩国
澳大利亚
越南
一列往返于石家庄与北京的“城际”快速列车沿途只停保定一站。这列快速列车需要准备多少种火车票?
石家庄
保定
北京
2+1=3(种) 3×2=6(种)
答:这列快速列车需要准备6种火车票,即石家庄 保定,石家庄 北京,保定 北京,保定 石家庄, 北京 石家庄,北京 保定。
我用连线的方法算。
一列往返于石家庄与北京的“城际”快速列车沿途只停保定一站。这列快速列车需要准备多少种火车票?
{69CF1AB2-1976-4502-BF36-3FF5EA218861}
石家庄
保定
北京
石家庄
保定
北京
发站
到站
石家庄→保定
石家庄→北京
保定→石家庄
保定→北京
北京→石家庄
北京→保定
还可以用列表的方法。
2×3=6(种)
答:这列快速列车需要准备6种火车票,即石家庄 保定,石家庄 北京,
保定 石家庄,保定 北京, 北京 石家庄,北京 保定。
聪聪、红红、亮亮和丫丫4人进行跳棋比赛。比赛实行单循环制,每2人都要赛一局。
(1)一共比赛几局?
我用的连线的方法。
聪聪
红红
亮亮
丫丫
3+2+1=6(局)
答:一共比赛6局。
聪聪、红红、亮亮和丫丫4人进行跳棋比赛。比赛实行单循环制,每2人都要赛一局。
(1)一共比赛几局?
{69CF1AB2-1976-4502-BF36-3FF5EA218861}
聪聪
红红
亮亮
丫丫
聪聪
红红
聪聪、红红
亮亮
聪聪、亮亮
红红、亮亮
丫丫
聪聪、丫丫
红红、丫丫
亮亮、丫丫
我用的列表法。
3+2+1=6(局) 答:一共比赛6局。
聪聪、红红、亮亮和丫丫4人进行跳棋比赛。比赛实行单循环制,每2人都要赛一局。
(2)最后一局,聪聪赢了丫丫。前几局,红红、丫丫和亮亮赢的局数相同。他们各赢了几局?
聪聪赢了 局;亮亮赢了 局;
红红赢了 局;丫丫赢了 局。
他们一共比赛了6局。分别是:
红红-聪聪
红红-亮亮
红红-丫丫
亮亮-聪聪
亮亮-丫丫
聪聪-丫丫
每人都进行了三场比赛,最后一局丫丫输了,那么丫丫最多只能赢2局,如果丫丫赢2局,红红、丫丫和亮亮赢的局数相同,那么红红、亮亮也要赢2局,聪聪赢1局,合起来就是7局,超过了6局,所以丫丫只能赢1局,红红、亮亮也是每人赢1局,聪聪赢3局。
3
1
1
1
五年级一共有5个班,每个班男生各组建了一支篮球队,现在学校开展篮球比赛,五年级的这5支篮球队都要参赛。每两支篮球队之间进行一场比赛,比赛实行单循环制,一共进行几场比赛?
我用的连线的方法。
五1班
五2班
五3班
五4班
五5班
4+3+2+1=10(场) 答:一共比赛10场。
五年级一共有5个班,每个班男生各组建了一支篮球队,现在学校开展篮球比赛,五年级的这5支篮球队都要参赛。每两支篮球队之间进行一场比赛,比赛实行单循环制,一共进行几场比赛?
{69CF1AB2-1976-4502-BF36-3FF5EA218861}
五1
五2
五3
五4
五5
五1
五2
五1、五2
五3
五1、五3
五2、五3
五4
五1、五4
五2、五4
五3、五4
五5
五1、五5
五2、五5
五3、五5
五4、五5
我用的列表法。
4+3+2+1=10(场) 答:一共比赛10场。
解决简单的比赛场次问题时,要做到不重复,不遗漏。
在寻找组合方案时,可以使用连线法、列表法等方法。
比赛场次问题
(比赛场次问题)
