人教版数学九年级上册:24.1.1 圆 同步练习(Word版附简略答案)
文档属性
| 名称 | 人教版数学九年级上册:24.1.1 圆 同步练习(Word版附简略答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 102.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 00:00:00 | ||
图片预览


文档简介
24.1.1 圆
1.下列条件中,能确定一个圆的是( )
A.以点O为圆心
B.以2 cm长为半径
C.以点O为圆心,以5 cm长为半径
D.经过点A
2.下列命题中正确的有( )
①弦是连接圆上任意两点的线段;②半径是弦;③直径是圆中最长的弦;④弧是半圆,半圆是弧.
A.1个 B.2个 C.3个 D.4个
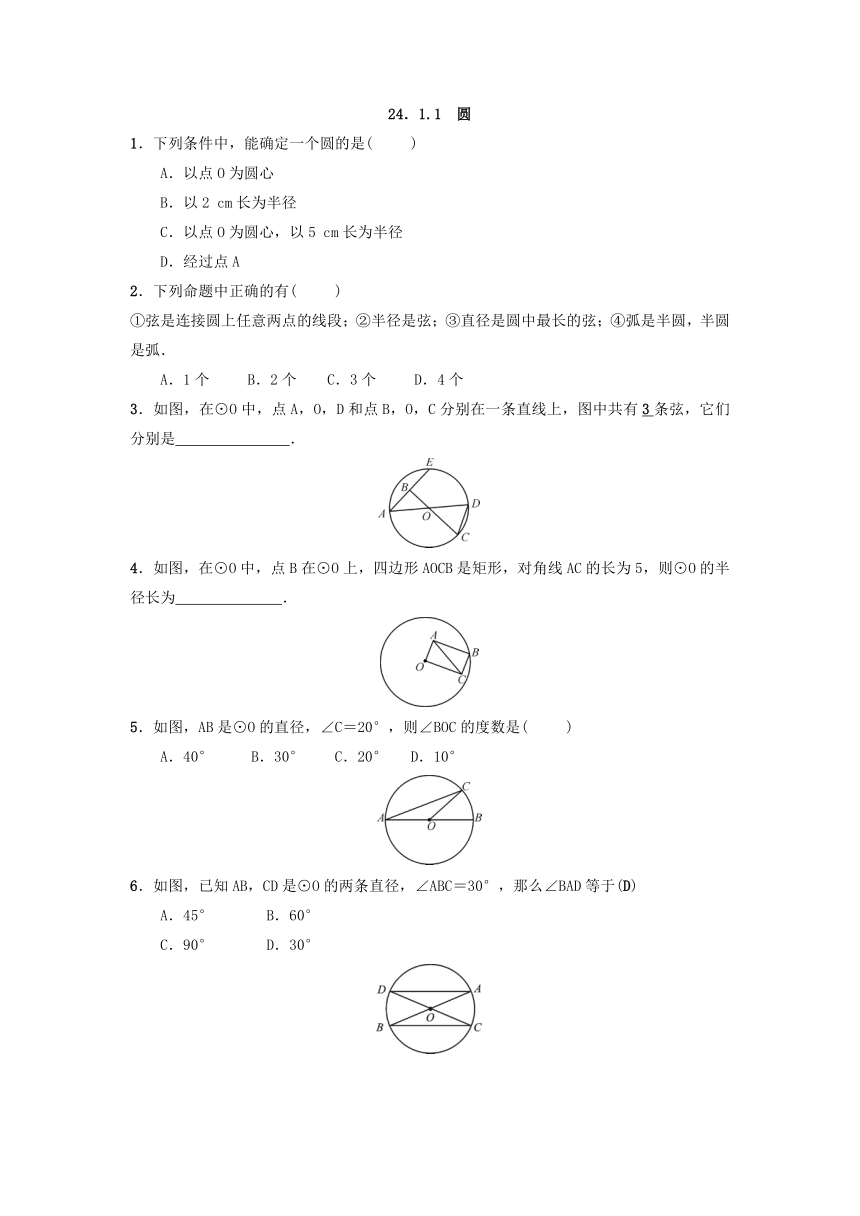
3.如图,在⊙O中,点A,O,D和点B,O,C分别在一条直线上,图中共有3条弦,它们分别是 .
4.如图,在⊙O中,点B在⊙O上,四边形AOCB是矩形,对角线AC的长为5,则⊙O的半径长为 .
5.如图,AB是⊙O的直径,∠C=20°,则∠BOC的度数是( )
A.40° B.30° C.20° D.10°
6.如图,已知AB,CD是⊙O的两条直径,∠ABC=30°,那么∠BAD等于(D)
A.45° B.60°
C.90° D.30°
7.如图,在△ABC中,BD,CE是两条高,点O为BC的中点,连接OD,OE,求证:B,C,D,E四个点在以点O为圆心的同一个圆上.
8.如图,AB,AC为⊙O的弦,连接CO,BO并延长,分别交弦AB,AC于点E,F,∠B=∠C.求证:CE=BF.
9.如图,在△ABC中,AB为⊙O的直径,∠B=60°,∠BOD=100°,则∠C的度数为( )
A.50° B.60° C.70° D.80°
10.下列四边形:①平行四边形;②菱形;③矩形;④正方形.其中四个顶点在同一个圆上的有( )
A.1个 B.2个 C.3个 D.4个
11.如图,A,B是⊙O上两点,若四边形ACBO是菱形,⊙O的半径为r,则点A与点B之间的距离为( )
A.r B.r C.R D.2r
12.已知A,B是半径为6 cm的圆上的两个不同的点,则弦长AB的取值范围是 cm.
13.如图,CE是⊙O的直径,AD的延长线与CE的延长线交于点B,若BD=OD,∠AOC=114°,求∠AOD的度数.
14.如图,AB是⊙O的弦,半径OC,OD分别交AB于点E,F,且AE=BF,请你找出线段OE与OF的数量关系,并给予证明.
15.如图,AB为⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E点,已知AB=2DE,∠E=18°,求∠AOC的度数.
16.如图,AB,CD是⊙O的直径,且AB⊥CD,点P,Q为上的任意两点,作PE⊥CD,PF⊥AB,QM⊥CD,QN⊥AB,则线段EF,MN的大小关系为EF MN.(填“<”“>”或“=”)
参考答案:
1.C
2.B
3. AE,DC,AD.
4.5.
5.A
6.D
7.证明:∵BD,CE是两条高,
∴∠BDC=∠BEC=90°.
∵△BEC为直角三角形,点O为BC的中点,
∴OE=OB=OC=BC.
同理:OD=OB=OC=BC.
∴OB=OC=OD=OE.
∴B,C,D,E在以点O为圆心的同一个圆上.
8.证明:∵OB,OC是⊙O的半径,
∴OB=OC.
又∵∠B=∠C,∠BOE=∠COF,
∴△EOB≌△FOC(ASA).
∴OE=OF.
∵CE=CO+OE,BF=BO+OF,
∴CE=BF.
9.C
10.B
11.B
12.013.解:设∠B=x°.
∵BD=OD,
∴∠DOB=∠B=x°.
∴∠ADO=∠DOB+∠B=2x°.
∵OA=OD,
∴∠A=∠ADO=2x°.
∵∠AOC=∠A+∠B,
∴2x+x=114.解得x=38.
∴∠AOD=180°-∠A-∠ADO=180°-4x°=180°-4×38°=28°.
14.解:OE=OF.
证明:∵OA,OB是⊙O的半径,
∴OA=OB.
∴∠OBA=∠OAB.
又∵AE=BF,
∴△OAE≌△OBF(SAS).
∴OE=OF.
15.
解:连接OD.
∵AB为⊙O的直径,OC,OD为半径,AB=2DE,
∴OC=OD=DE.
∴∠DOE=∠E,∠OCE=∠ODC.
又∵∠ODC=∠DOE+∠E,
∴∠OCE=∠ODC=2∠E.
∵∠E=18°,∴∠OCE=36°.
∴∠AOC=∠OCE+∠E=36°+18°=54°.
16.=
1.下列条件中,能确定一个圆的是( )
A.以点O为圆心
B.以2 cm长为半径
C.以点O为圆心,以5 cm长为半径
D.经过点A
2.下列命题中正确的有( )
①弦是连接圆上任意两点的线段;②半径是弦;③直径是圆中最长的弦;④弧是半圆,半圆是弧.
A.1个 B.2个 C.3个 D.4个
3.如图,在⊙O中,点A,O,D和点B,O,C分别在一条直线上,图中共有3条弦,它们分别是 .
4.如图,在⊙O中,点B在⊙O上,四边形AOCB是矩形,对角线AC的长为5,则⊙O的半径长为 .
5.如图,AB是⊙O的直径,∠C=20°,则∠BOC的度数是( )
A.40° B.30° C.20° D.10°
6.如图,已知AB,CD是⊙O的两条直径,∠ABC=30°,那么∠BAD等于(D)
A.45° B.60°
C.90° D.30°
7.如图,在△ABC中,BD,CE是两条高,点O为BC的中点,连接OD,OE,求证:B,C,D,E四个点在以点O为圆心的同一个圆上.
8.如图,AB,AC为⊙O的弦,连接CO,BO并延长,分别交弦AB,AC于点E,F,∠B=∠C.求证:CE=BF.
9.如图,在△ABC中,AB为⊙O的直径,∠B=60°,∠BOD=100°,则∠C的度数为( )
A.50° B.60° C.70° D.80°
10.下列四边形:①平行四边形;②菱形;③矩形;④正方形.其中四个顶点在同一个圆上的有( )
A.1个 B.2个 C.3个 D.4个
11.如图,A,B是⊙O上两点,若四边形ACBO是菱形,⊙O的半径为r,则点A与点B之间的距离为( )
A.r B.r C.R D.2r
12.已知A,B是半径为6 cm的圆上的两个不同的点,则弦长AB的取值范围是 cm.
13.如图,CE是⊙O的直径,AD的延长线与CE的延长线交于点B,若BD=OD,∠AOC=114°,求∠AOD的度数.
14.如图,AB是⊙O的弦,半径OC,OD分别交AB于点E,F,且AE=BF,请你找出线段OE与OF的数量关系,并给予证明.
15.如图,AB为⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E点,已知AB=2DE,∠E=18°,求∠AOC的度数.
16.如图,AB,CD是⊙O的直径,且AB⊥CD,点P,Q为上的任意两点,作PE⊥CD,PF⊥AB,QM⊥CD,QN⊥AB,则线段EF,MN的大小关系为EF MN.(填“<”“>”或“=”)
参考答案:
1.C
2.B
3. AE,DC,AD.
4.5.
5.A
6.D
7.证明:∵BD,CE是两条高,
∴∠BDC=∠BEC=90°.
∵△BEC为直角三角形,点O为BC的中点,
∴OE=OB=OC=BC.
同理:OD=OB=OC=BC.
∴OB=OC=OD=OE.
∴B,C,D,E在以点O为圆心的同一个圆上.
8.证明:∵OB,OC是⊙O的半径,
∴OB=OC.
又∵∠B=∠C,∠BOE=∠COF,
∴△EOB≌△FOC(ASA).
∴OE=OF.
∵CE=CO+OE,BF=BO+OF,
∴CE=BF.
9.C
10.B
11.B
12.0
∵BD=OD,
∴∠DOB=∠B=x°.
∴∠ADO=∠DOB+∠B=2x°.
∵OA=OD,
∴∠A=∠ADO=2x°.
∵∠AOC=∠A+∠B,
∴2x+x=114.解得x=38.
∴∠AOD=180°-∠A-∠ADO=180°-4x°=180°-4×38°=28°.
14.解:OE=OF.
证明:∵OA,OB是⊙O的半径,
∴OA=OB.
∴∠OBA=∠OAB.
又∵AE=BF,
∴△OAE≌△OBF(SAS).
∴OE=OF.
15.
解:连接OD.
∵AB为⊙O的直径,OC,OD为半径,AB=2DE,
∴OC=OD=DE.
∴∠DOE=∠E,∠OCE=∠ODC.
又∵∠ODC=∠DOE+∠E,
∴∠OCE=∠ODC=2∠E.
∵∠E=18°,∴∠OCE=36°.
∴∠AOC=∠OCE+∠E=36°+18°=54°.
16.=
同课章节目录
