1.5.1 有理数的乘方(第一课时) 课件(共23张PPT)
文档属性
| 名称 | 1.5.1 有理数的乘方(第一课时) 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 00:00:00 | ||
图片预览







文档简介
1.5.1 有理数的乘方
第一章 有理数
第一课时 有理数的乘方
人教版 七上
1)先算乘除,再算加减,同级运算从左往右依次计算;
2)如有括号,先算括号内的。
有理数混合运算的顺序:
课前回顾
1、理解有理数乘方的意义;
2、掌握有理数乘方的运算;
3、培养学生观察、分析、归纳和概括的能力。
重点
理解有理数乘方的意义。
难点
掌握有理数乘方的运算。
学习目标
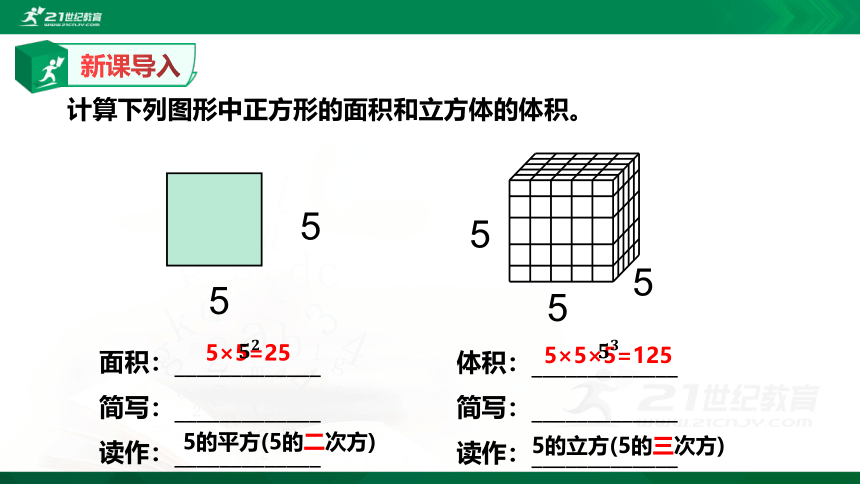
计算下列图形中正方形的面积和立方体的体积。
5
5
5
5
5
面积:_____________
简写:_____________
读作:_____________
5的平方(5的二次方)
5×5=25
????????
?
体积:_____________
简写:_____________
读作:_____________
5的立方(5的三次方)
5×5×5=125
????????
?
新课导入
那么,类似地
1)(-2)× (-2) × (-2) × (-2) =
读作:________________________________
2) (- ????????)×(- ?????????)×(- ?????????)×(???????????) ×(???????????)?=
读作: ________________________________
?
(?2)4
?
(??25?)5
?
-2的四次方
??25的五次方
?
观察以上这些式子有什么共同点?
1. 乘法运算。
2. 相乘的因数相同。
探究新知
5×5×???×5
n个5
= 5
那么,n个5相乘后的结果呢?
n
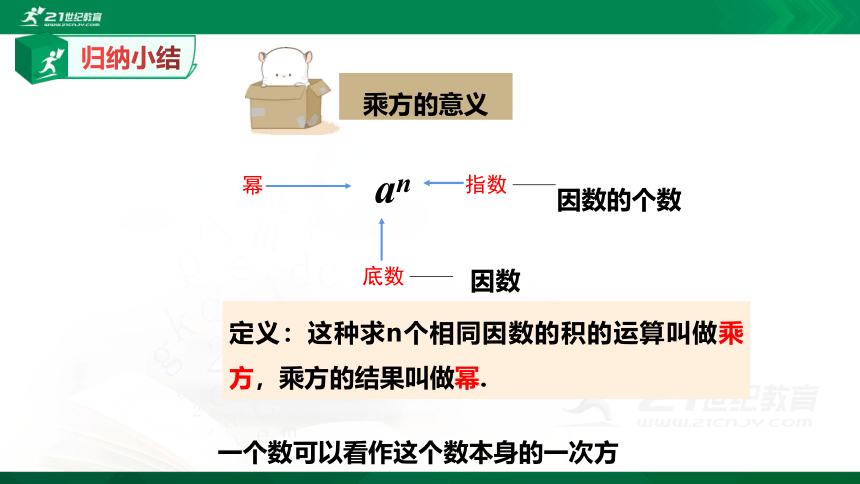
一般地,n个相同的因数a相乘,即a×a×a…×a,记作????????,
读作:a的n次方。
?
n个a
幂
指数
因数的个数
底数
因数
an
定义:这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
一个数可以看作这个数本身的一次方
乘方的意义
归纳小结
填空:
记作:___________,读作:________________
的六次方
记作:___________,读作:________________
-24
2的四次方的相反数
想一想:(-2)4与-24一样吗?为什么?
针对练习
填空:
(1)在94中,底数是______, 指数是______,
读作: ______________或_________________.
9
4
9的四次方
9的四次幂
提示:一个数可以看作这个数本身的一次方.
(2)在5中,底数是______, 指数是______,
5
1
5=51
指数1通常省略不写
针对练习
例1 计算:
(1) (-4)3; (2) (-2)4; (3) .
(2) (-2)4 =(-2)×(-2)×(-2)×(-2)=16;
(1) (-4)3 =(-4)×(-4)×(-4)=-64;
解:
如何进行乘方运算呢?
表示3个-4相乘.
乘方运算转化为乘法运算.
典例分析
问题1:从前面的计算中你能发现什么规律?
当指数是____数时,负数的幂是_____数;
(-4)3=(-4)×(-4)×(-4)=-64;
(-2)4=(-2)×(-2)×(-2)×(-2)=16;
当指数是____数时,负数的幂是_____数;
正
奇
负
偶
归纳小结
根据有理数乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数;
正数的任何次幂都是正数,
0的任何正整数次幂都是0.
归纳小结
{F5AB1C69-6EDB-4FF4-983F-18BD219EF322}
底数
指数
结果正负
结果
针对练习
尝试用计算器计算(-8)5和(-3)6 .
不同的计算器可能操作方法不同,具体见计算器说明书。
典例分析
典例1??????????可表示为( )
A.(?????)×???? B.(-3)+(-3) C.?(????×????) D.(?????)×(?????)
?
【答案】C
【详解】解:?32=?(3×3),故选:C.
?
课堂练习
变式1-1 下列代数式的值一定是正数的是( )
A.a B.a+9 C.a2+1 D.|a+1|
【答案】C
【详解】
解:A、a可以表示任意实数,故本选项错误;
B、当a≤?9时,a+9是非正数,故本选项错误;
C、a2+1≥1,故本选项正确;
D、当a=?1时,|a+1|=0,故本选项错误.
故选:C.
典例2 若|x+1|+(y-2019)2=0,则????????=( )。
A.0 B.1 C.????? D.2019
?
【答案】C
【详解】
解:根据题意,得:????+1=0,?????2019=0,
解得:????=?1,????=2019,所以????????=?12019=?1.
故选:C.
?
变式2-1 观察下列等式:21=2,22=4,23=8,24=16,25=32,26=64…,则22018的末位数是( )
A.2 B.4 C.6 D.8
【答案】B
【提示】
由题中可以看出,以2为底的幂的末位数字是2,4,8,6依次循环的,故个位的数字是以4为周期变化的,用2018÷4,计算一下看看有多少个周期即可.
【详解】
解:以2为底的幂的末位数字是2,4,8,6依次循环的,
∵2018÷4=504…2,
∴22018的个位数字是4. 故选B.
典例3 对于?????????与?????????,下列说法正确的是( ).
A.底数不同,结果不同 B.底数不同,结果相同
C.底数相同,结果不同 D.底数相同,结果相同
?
【答案】A
【详解】
解:?32的底数为3,?32的底数为-3,?32=?9,?32=9,
故?32与?32底数不同,结果不同,
故选:A.
?
变式3-1 下列各数:(﹣1)2、﹣(﹣3),﹣|﹣????????|,(﹣2)3,(﹣2)×(﹣3),其中负数有( )
A.1个 B.2个 C.3个 D.4个
?
【答案】B
【详解】
解:在所列实数中,负数有﹣|﹣12|,(﹣2)3这2个,
故选:B.
?
典例4 一根1米长的绳子,第一次剪去一半,第二次剪去剩下的一半,如此下去,第六次后剩下的绳子长度为( )
A.????????????米 B.????????????米 C.????????????米 D.????????????????米
?
【答案】C
【提示】根据乘方的意义和题意可知:第2次后剩下的绳子的长度为(12)2米,那么依此类推得到第六次后剩下的绳子的长度为(12)6米.
【详解】∵1-12=12,∴第2次后剩下的绳子的长度为(12)2米;
依此类推第六次后剩下的绳子的长度为(12)6米.故选C.
?
变式4-1 某种细菌在培养过程中,每半小时分裂一次(由一个分裂成两个),若这种细菌由1个分裂为64个,则这个过程要经过( )
A.1小时 B.2小时 C.3小时 D.4小时
【答案】C
【详解】
解:根据已知可知:一个细胞第一次分裂成21个,
第二次分裂成22个,第三次分裂成23个,
由上述规律可知,第n次时细胞分裂的个数为2n个,
设第x次分裂成64个,由题意得2x=64,解得x=6,
即第6次分裂细菌分裂成64个,
答:由每半小时分裂一次,此细菌由1个分裂成64个,共花费了3个小时.故答案选C.
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数
(2)负数的奇次幂是负数,负数的偶次幂是正数
(3)零的正整数次幂都是零
幂
指数
底数
课堂小结
第一章 有理数
第一课时 有理数的乘方
人教版 七上
1)先算乘除,再算加减,同级运算从左往右依次计算;
2)如有括号,先算括号内的。
有理数混合运算的顺序:
课前回顾
1、理解有理数乘方的意义;
2、掌握有理数乘方的运算;
3、培养学生观察、分析、归纳和概括的能力。
重点
理解有理数乘方的意义。
难点
掌握有理数乘方的运算。
学习目标
计算下列图形中正方形的面积和立方体的体积。
5
5
5
5
5
面积:_____________
简写:_____________
读作:_____________
5的平方(5的二次方)
5×5=25
????????
?
体积:_____________
简写:_____________
读作:_____________
5的立方(5的三次方)
5×5×5=125
????????
?
新课导入
那么,类似地
1)(-2)× (-2) × (-2) × (-2) =
读作:________________________________
2) (- ????????)×(- ?????????)×(- ?????????)×(???????????) ×(???????????)?=
读作: ________________________________
?
(?2)4
?
(??25?)5
?
-2的四次方
??25的五次方
?
观察以上这些式子有什么共同点?
1. 乘法运算。
2. 相乘的因数相同。
探究新知
5×5×???×5
n个5
= 5
那么,n个5相乘后的结果呢?
n
一般地,n个相同的因数a相乘,即a×a×a…×a,记作????????,
读作:a的n次方。
?
n个a
幂
指数
因数的个数
底数
因数
an
定义:这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
一个数可以看作这个数本身的一次方
乘方的意义
归纳小结
填空:
记作:___________,读作:________________
的六次方
记作:___________,读作:________________
-24
2的四次方的相反数
想一想:(-2)4与-24一样吗?为什么?
针对练习
填空:
(1)在94中,底数是______, 指数是______,
读作: ______________或_________________.
9
4
9的四次方
9的四次幂
提示:一个数可以看作这个数本身的一次方.
(2)在5中,底数是______, 指数是______,
5
1
5=51
指数1通常省略不写
针对练习
例1 计算:
(1) (-4)3; (2) (-2)4; (3) .
(2) (-2)4 =(-2)×(-2)×(-2)×(-2)=16;
(1) (-4)3 =(-4)×(-4)×(-4)=-64;
解:
如何进行乘方运算呢?
表示3个-4相乘.
乘方运算转化为乘法运算.
典例分析
问题1:从前面的计算中你能发现什么规律?
当指数是____数时,负数的幂是_____数;
(-4)3=(-4)×(-4)×(-4)=-64;
(-2)4=(-2)×(-2)×(-2)×(-2)=16;
当指数是____数时,负数的幂是_____数;
正
奇
负
偶
归纳小结
根据有理数乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数;
正数的任何次幂都是正数,
0的任何正整数次幂都是0.
归纳小结
{F5AB1C69-6EDB-4FF4-983F-18BD219EF322}
底数
指数
结果正负
结果
针对练习
尝试用计算器计算(-8)5和(-3)6 .
不同的计算器可能操作方法不同,具体见计算器说明书。
典例分析
典例1??????????可表示为( )
A.(?????)×???? B.(-3)+(-3) C.?(????×????) D.(?????)×(?????)
?
【答案】C
【详解】解:?32=?(3×3),故选:C.
?
课堂练习
变式1-1 下列代数式的值一定是正数的是( )
A.a B.a+9 C.a2+1 D.|a+1|
【答案】C
【详解】
解:A、a可以表示任意实数,故本选项错误;
B、当a≤?9时,a+9是非正数,故本选项错误;
C、a2+1≥1,故本选项正确;
D、当a=?1时,|a+1|=0,故本选项错误.
故选:C.
典例2 若|x+1|+(y-2019)2=0,则????????=( )。
A.0 B.1 C.????? D.2019
?
【答案】C
【详解】
解:根据题意,得:????+1=0,?????2019=0,
解得:????=?1,????=2019,所以????????=?12019=?1.
故选:C.
?
变式2-1 观察下列等式:21=2,22=4,23=8,24=16,25=32,26=64…,则22018的末位数是( )
A.2 B.4 C.6 D.8
【答案】B
【提示】
由题中可以看出,以2为底的幂的末位数字是2,4,8,6依次循环的,故个位的数字是以4为周期变化的,用2018÷4,计算一下看看有多少个周期即可.
【详解】
解:以2为底的幂的末位数字是2,4,8,6依次循环的,
∵2018÷4=504…2,
∴22018的个位数字是4. 故选B.
典例3 对于?????????与?????????,下列说法正确的是( ).
A.底数不同,结果不同 B.底数不同,结果相同
C.底数相同,结果不同 D.底数相同,结果相同
?
【答案】A
【详解】
解:?32的底数为3,?32的底数为-3,?32=?9,?32=9,
故?32与?32底数不同,结果不同,
故选:A.
?
变式3-1 下列各数:(﹣1)2、﹣(﹣3),﹣|﹣????????|,(﹣2)3,(﹣2)×(﹣3),其中负数有( )
A.1个 B.2个 C.3个 D.4个
?
【答案】B
【详解】
解:在所列实数中,负数有﹣|﹣12|,(﹣2)3这2个,
故选:B.
?
典例4 一根1米长的绳子,第一次剪去一半,第二次剪去剩下的一半,如此下去,第六次后剩下的绳子长度为( )
A.????????????米 B.????????????米 C.????????????米 D.????????????????米
?
【答案】C
【提示】根据乘方的意义和题意可知:第2次后剩下的绳子的长度为(12)2米,那么依此类推得到第六次后剩下的绳子的长度为(12)6米.
【详解】∵1-12=12,∴第2次后剩下的绳子的长度为(12)2米;
依此类推第六次后剩下的绳子的长度为(12)6米.故选C.
?
变式4-1 某种细菌在培养过程中,每半小时分裂一次(由一个分裂成两个),若这种细菌由1个分裂为64个,则这个过程要经过( )
A.1小时 B.2小时 C.3小时 D.4小时
【答案】C
【详解】
解:根据已知可知:一个细胞第一次分裂成21个,
第二次分裂成22个,第三次分裂成23个,
由上述规律可知,第n次时细胞分裂的个数为2n个,
设第x次分裂成64个,由题意得2x=64,解得x=6,
即第6次分裂细菌分裂成64个,
答:由每半小时分裂一次,此细菌由1个分裂成64个,共花费了3个小时.故答案选C.
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数
(2)负数的奇次幂是负数,负数的偶次幂是正数
(3)零的正整数次幂都是零
幂
指数
底数
课堂小结
