11.3角的平分线的性质2
文档属性
| 名称 | 11.3角的平分线的性质2 |
|
|
| 格式 | zip | ||
| 文件大小 | 42.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-04 00:00:00 | ||
图片预览

文档简介
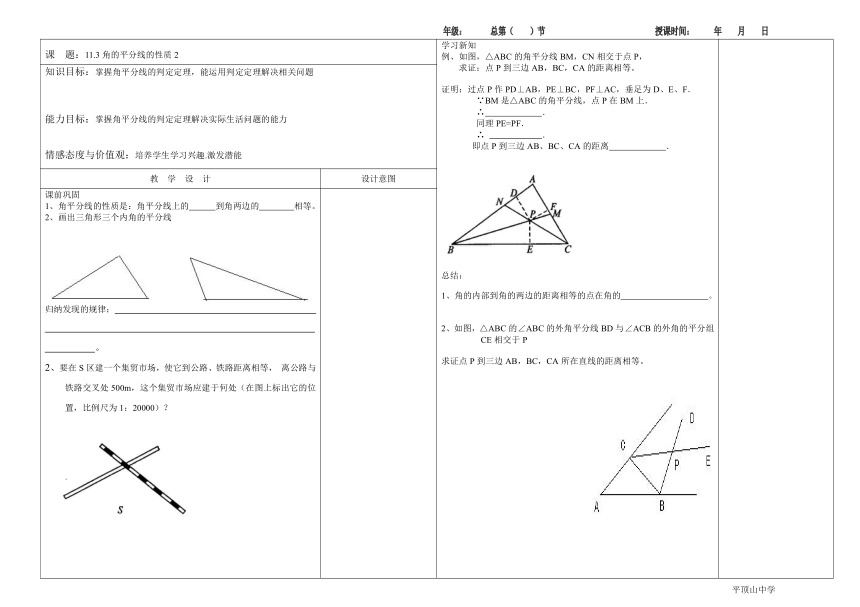
课 题:11.3角的平分线的性质2 学习新知例、如图,△ABC的角平分线BM,CN相交于点P,求证:点P到三边AB,BC,CA的距离相等。证明:过点P作PD⊥AB,PE⊥BC,PF⊥AC,垂足为D、E、F. ∵BM是△ABC的角平分线,点P在BM上. ∴ . 同理PE=PF. ∴ . 即点P到三边AB、BC、CA的距离 .总结:1、角的内部到角的两边的距离相等的点在角的 。2、如图,△ABC的∠ABC的外角平分线BD与∠ACB的外角的平分组CE相交于P求证点P到三边AB,BC,CA所在直线的距离相等。
知识目标:掌握角平分线的判定定理,能运用判定定理解决相关问题能力目标:掌握角平分线的判定定理解决实际生活问题的能力情感态度与价值观:培养学生学习兴趣.激发潜能
教 学 设 计 设计意图
课前巩固1、角平分线的性质是:角平分线上的 到角两边的 相等。2、画出三角形三个内角的平分线归纳发现的规律: 。2、要在S区建一个集贸市场,使它到公路、铁路距离相等,离公路与铁路交叉处500m,这个集贸市场应建于何处(在图上标出它的位置,比例尺为1:20000)?
课堂练习:1、如图,OC是∠AOB的平分线,P是OC上的一点,PD⊥OA交OA于D,PE⊥OB交OB于E,F是OC上的另一点,连接DF,EF,求证DF=EF2、在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,AB=7㎝,AC=3㎝,求BE的长。 如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC,求证∠BAO=∠CAO
教后记: 组长签字:
教务处签字:
E
D
C
B
A
平顶山中学
知识目标:掌握角平分线的判定定理,能运用判定定理解决相关问题能力目标:掌握角平分线的判定定理解决实际生活问题的能力情感态度与价值观:培养学生学习兴趣.激发潜能
教 学 设 计 设计意图
课前巩固1、角平分线的性质是:角平分线上的 到角两边的 相等。2、画出三角形三个内角的平分线归纳发现的规律: 。2、要在S区建一个集贸市场,使它到公路、铁路距离相等,离公路与铁路交叉处500m,这个集贸市场应建于何处(在图上标出它的位置,比例尺为1:20000)?
课堂练习:1、如图,OC是∠AOB的平分线,P是OC上的一点,PD⊥OA交OA于D,PE⊥OB交OB于E,F是OC上的另一点,连接DF,EF,求证DF=EF2、在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,AB=7㎝,AC=3㎝,求BE的长。 如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC,求证∠BAO=∠CAO
教后记: 组长签字:
教务处签字:
E
D
C
B
A
平顶山中学
