人教A版(2019)必修 第一册第二章 一元二次函数、方程和不等式2.1 等式性质与不等式性质(1)-课件(20张PPT)
文档属性
| 名称 | 人教A版(2019)必修 第一册第二章 一元二次函数、方程和不等式2.1 等式性质与不等式性质(1)-课件(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 460.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 00:00:00 | ||
图片预览







文档简介
等式性质与不等式性质(1)
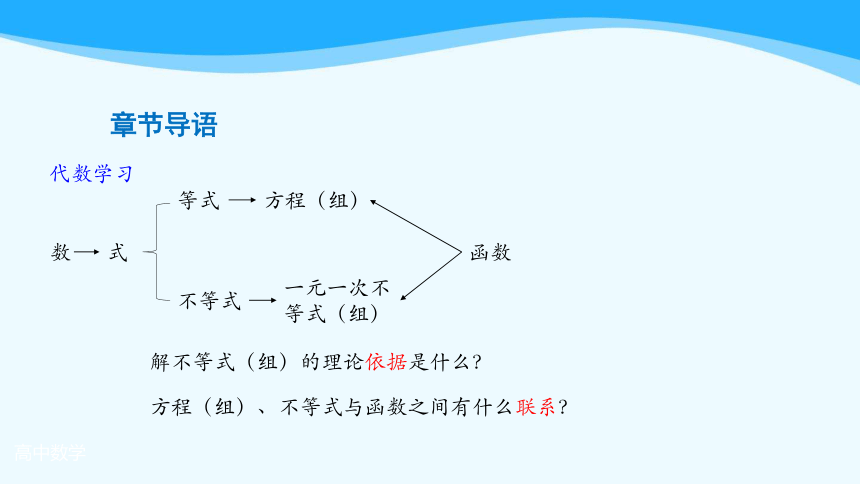
章节导语
数
式
等式
不等式
方程(组)
一元一次不等式(组)
函数
解不等式(组)的理论依据是什么?
方程(组)、不等式与函数之间有什么联系?
代数学习
复习回顾
问题1:常见的不等关系有哪些?你能用文字语言和符号语言表述吗?
{5940675A-B579-460E-94D1-54222C63F5DA}文字语言
符号语言
大于
>
小于
<
大于或等于(不小于)
小于或等于(不大于)
复习回顾
问题2:你能用不等式或不等式组表示下列问题中的不等关系吗?
(1)某路段限速40 km/h;
解:
设在该路段行驶的汽车的速度为 v km/h,“限速40 km/h”就是 v 的大小不能超过40,于是0 <v 40.
复习回顾
问题2:你能用不等式或不等式组表示下列问题中的不等关系吗?
(2)某品牌酸奶的质量检查规定,酸奶中脂肪的含量 f 应不少于2.5%,蛋白质的含量 p 应不少于2.3%;
解:
由题意,得 f??????2.5%,p??????2.3%.
?
复习回顾
问题2:你能用不等式或不等式组表示下列问题中的不等关系吗?
(3)三角形两边之和大于第三边、两边之差小于第三边;
解:
设△ABC的三条边为a,b,c,则 a + b > c ,a – b < c .
注:a + c > b ,a – c < b 等其它合理形式也正确.
复习回顾
问题2:你能用不等式或不等式组表示下列问题中的不等关系吗?
(4)连接直线外一点与直线上各点的所有线段中,垂线段最短.
解:
如图,设C是直线AB外的任意一点,CD⊥AB于点D,E是直线AB上不同于D的任意一点,连接线段CE,则CD<CE.
C
D
E
A
B
复习回顾
小结:用不等式表示实际问题中的不等关系的方法.
数学抽象
温故知新
问题3:你能用不等式表示并解决下面的问题吗?
某种杂志原以每本2.5元的价格销售,可以售出8万本,据市场调查,杂志的单价每提高0.1元,销售就可能减少2000本. 如何定价才能使提价后的销售总收入不低于20万?
解:设提价后每本杂志的定价为 x 元.
销售量: (8??x?2.50.1×0.2)万本.
?
不等关系:销售总收入不低于20万.
销售总收入: (8??x?2.50.1×0.2)x万元.
?
温故知新
问题3:你能用不等式表示并解决下面的问题吗?
某种杂志原以每本2.5元的价格销售,可以售出8万本,据市场调查,杂志的单价每提高0.1元,销售就可能减少2000本. 如何定价才能使提价后的销售总收入不低于20万?
解:设提价后每本杂志的定价为 x 元.
不等关系:销售总收入不低于20万.
(8??x?2.50.1×0.2)x 20.
?
温故知新
问题3:你能用不等式表示并解决下面的问题吗?
某种杂志原以每本2.5元的价格销售,可以售出8万本,据市场调查,杂志的单价每提高0.1元,销售就可能减少2000本. 如何定价才能使提价后的销售总收入不低于20万?
解:设提价后每本杂志的定价为 x 元.
不等关系:销售总收入不低于20万.
温故知新
追问:解方程是主要依据是什么?类比解方程,你能找到解不等式的主要依据吗?
解方程的主要依据:等式性质.
解不等式的主要依据:不等式性质.
类比
移项,系数化为1等运算手段.
比较两个式子的大小关系
关于实数a,b大小的比较,有以下基本事实:
如果a?b是正数,那么a>b;如果a?b等于0,那么a=b;如果a?b是负数,那么a<b.反过来也对.
?
温故知新
问题4:如何比较两个式子的大小关系?
作差法:比较两个实数(式子)大小关系的方法.
比较大小关系
研究差值符号
运算
学以致用
例1:比较x+2x+3和(x+1)(x+4)的大小关系.
?
分析:若要比较两者的大小,只需比较它们的差与0的关系.
解:x+2x+3?(x+1)(x+4)
?
=x2+5x+6?(x2+5x+4)
?
=2
?
>0,
?
∴ x+2x+3>(x+1)(x+4).
?
学以致用
例2:右图是在北京召开的第24届国际数学家大会的会标,会标是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去像一个风车,代表中国人民热情好客.你能在这个图中找出一些相等关系和不等关系吗?
D
A
B
C
G
H
F
E
正方形ABCD的面积大于4个直角三角形的面积和.
4×12ab
?
学以致用
例2:你能在这个图中找出一些相等关系和不等关系吗?
正方形
ABCD的面积
4个直角三角形的面积和
a2+b2
?
2ab
?
D
A
B
C
G
H
F
E
a2+b2
?
a
b
a≠b
?
>
追问1:如果直角三角形的两条直角边边长分别为a,b (a≠b),你能将发现的不等关系用不等式表示吗?
?
大于
学以致用
例2:你能在这个图中找出一些相等关系和不等关系吗?
4个直角三角形的面积和
2ab
?
D
A
B
C
G
H
F
E
a2+b2
?
a
b
=
?
追问2:如果直角三角形的两条直角边边长相等(a=b),不等式 a2+b2>2ab还成立吗?
?
等于
正方形
ABCD的面积
a2+b2
?
学以致用
例2:你能在这个图中找出一些相等关系和不等关系吗?
D
A
B
C
G
H
F
E
a2+b2
?
a
b
追问3:?a,b∈R,a2+b2??????2ab.
这个猜想成立吗?请证明或证伪.
?
解:a2+b2?2ab
?
=?(a?b)2
?
?????0,
?
∴ a2+b2??????2ab.
?
当且仅当a=b时,等号成立.
?
重要不等式
课堂小结
实际问题
不等关系
两个实数大小关系的基本事实(作差法)
不等式
不等式
性质
数学抽象
?
等式性质与不等式性质(1)
谢谢观看,再见.
章节导语
数
式
等式
不等式
方程(组)
一元一次不等式(组)
函数
解不等式(组)的理论依据是什么?
方程(组)、不等式与函数之间有什么联系?
代数学习
复习回顾
问题1:常见的不等关系有哪些?你能用文字语言和符号语言表述吗?
{5940675A-B579-460E-94D1-54222C63F5DA}文字语言
符号语言
大于
>
小于
<
大于或等于(不小于)
小于或等于(不大于)
复习回顾
问题2:你能用不等式或不等式组表示下列问题中的不等关系吗?
(1)某路段限速40 km/h;
解:
设在该路段行驶的汽车的速度为 v km/h,“限速40 km/h”就是 v 的大小不能超过40,于是0 <v 40.
复习回顾
问题2:你能用不等式或不等式组表示下列问题中的不等关系吗?
(2)某品牌酸奶的质量检查规定,酸奶中脂肪的含量 f 应不少于2.5%,蛋白质的含量 p 应不少于2.3%;
解:
由题意,得 f??????2.5%,p??????2.3%.
?
复习回顾
问题2:你能用不等式或不等式组表示下列问题中的不等关系吗?
(3)三角形两边之和大于第三边、两边之差小于第三边;
解:
设△ABC的三条边为a,b,c,则 a + b > c ,a – b < c .
注:a + c > b ,a – c < b 等其它合理形式也正确.
复习回顾
问题2:你能用不等式或不等式组表示下列问题中的不等关系吗?
(4)连接直线外一点与直线上各点的所有线段中,垂线段最短.
解:
如图,设C是直线AB外的任意一点,CD⊥AB于点D,E是直线AB上不同于D的任意一点,连接线段CE,则CD<CE.
C
D
E
A
B
复习回顾
小结:用不等式表示实际问题中的不等关系的方法.
数学抽象
温故知新
问题3:你能用不等式表示并解决下面的问题吗?
某种杂志原以每本2.5元的价格销售,可以售出8万本,据市场调查,杂志的单价每提高0.1元,销售就可能减少2000本. 如何定价才能使提价后的销售总收入不低于20万?
解:设提价后每本杂志的定价为 x 元.
销售量: (8??x?2.50.1×0.2)万本.
?
不等关系:销售总收入不低于20万.
销售总收入: (8??x?2.50.1×0.2)x万元.
?
温故知新
问题3:你能用不等式表示并解决下面的问题吗?
某种杂志原以每本2.5元的价格销售,可以售出8万本,据市场调查,杂志的单价每提高0.1元,销售就可能减少2000本. 如何定价才能使提价后的销售总收入不低于20万?
解:设提价后每本杂志的定价为 x 元.
不等关系:销售总收入不低于20万.
(8??x?2.50.1×0.2)x 20.
?
温故知新
问题3:你能用不等式表示并解决下面的问题吗?
某种杂志原以每本2.5元的价格销售,可以售出8万本,据市场调查,杂志的单价每提高0.1元,销售就可能减少2000本. 如何定价才能使提价后的销售总收入不低于20万?
解:设提价后每本杂志的定价为 x 元.
不等关系:销售总收入不低于20万.
温故知新
追问:解方程是主要依据是什么?类比解方程,你能找到解不等式的主要依据吗?
解方程的主要依据:等式性质.
解不等式的主要依据:不等式性质.
类比
移项,系数化为1等运算手段.
比较两个式子的大小关系
关于实数a,b大小的比较,有以下基本事实:
如果a?b是正数,那么a>b;如果a?b等于0,那么a=b;如果a?b是负数,那么a<b.反过来也对.
?
温故知新
问题4:如何比较两个式子的大小关系?
作差法:比较两个实数(式子)大小关系的方法.
比较大小关系
研究差值符号
运算
学以致用
例1:比较x+2x+3和(x+1)(x+4)的大小关系.
?
分析:若要比较两者的大小,只需比较它们的差与0的关系.
解:x+2x+3?(x+1)(x+4)
?
=x2+5x+6?(x2+5x+4)
?
=2
?
>0,
?
∴ x+2x+3>(x+1)(x+4).
?
学以致用
例2:右图是在北京召开的第24届国际数学家大会的会标,会标是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去像一个风车,代表中国人民热情好客.你能在这个图中找出一些相等关系和不等关系吗?
D
A
B
C
G
H
F
E
正方形ABCD的面积大于4个直角三角形的面积和.
4×12ab
?
学以致用
例2:你能在这个图中找出一些相等关系和不等关系吗?
正方形
ABCD的面积
4个直角三角形的面积和
a2+b2
?
2ab
?
D
A
B
C
G
H
F
E
a2+b2
?
a
b
a≠b
?
>
追问1:如果直角三角形的两条直角边边长分别为a,b (a≠b),你能将发现的不等关系用不等式表示吗?
?
大于
学以致用
例2:你能在这个图中找出一些相等关系和不等关系吗?
4个直角三角形的面积和
2ab
?
D
A
B
C
G
H
F
E
a2+b2
?
a
b
=
?
追问2:如果直角三角形的两条直角边边长相等(a=b),不等式 a2+b2>2ab还成立吗?
?
等于
正方形
ABCD的面积
a2+b2
?
学以致用
例2:你能在这个图中找出一些相等关系和不等关系吗?
D
A
B
C
G
H
F
E
a2+b2
?
a
b
追问3:?a,b∈R,a2+b2??????2ab.
这个猜想成立吗?请证明或证伪.
?
解:a2+b2?2ab
?
=?(a?b)2
?
?????0,
?
∴ a2+b2??????2ab.
?
当且仅当a=b时,等号成立.
?
重要不等式
课堂小结
实际问题
不等关系
两个实数大小关系的基本事实(作差法)
不等式
不等式
性质
数学抽象
?
等式性质与不等式性质(1)
谢谢观看,再见.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
