人教版高二物理选修3-2 原创课件-4.4法拉第电磁感应定律27张PPT
文档属性
| 名称 | 人教版高二物理选修3-2 原创课件-4.4法拉第电磁感应定律27张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 594.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-12-02 23:23:07 | ||
图片预览






文档简介
(共27张PPT)
第十一章
电磁感应
法拉第电磁感应定律
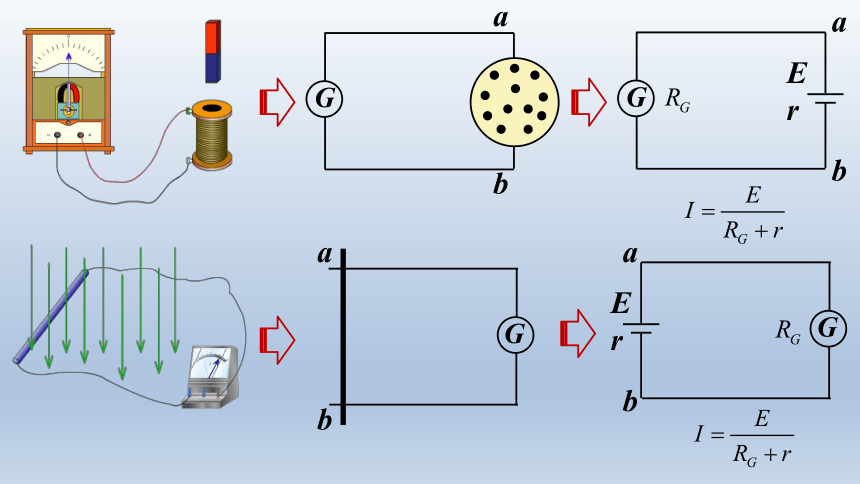
G
E
r
a
b
G
E
r
a
b
G
a
b
G
a
b
认识感应电路问题:
1.
在电磁感应现象中产生的电动势称感应电动势。
2.产生感应电动势的那部分导体相当于电源。
3.产生感应电动势只需要磁通量发生变化,不需要闭合回路;
产生感应电流才需要磁通量发生变化和闭合回路。
4.区分电动势与路端电压的区别:路端电压指的是外电路的电压,只有开路时,路端电压才等于电动势。
5.感应电动势的正负极可以根据楞次定律来判断。
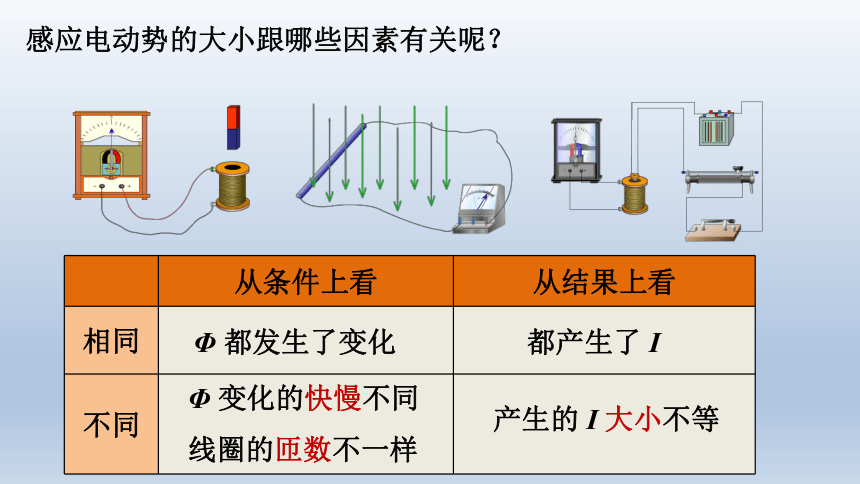
感应电动势的大小跟哪些因素有关呢?
从条件上看
从结果上看
相同
不同
Φ
变化的快慢不同
线圈的匝数不一样
Φ
都发生了变化
都产生了
I
产生的
I
大小不等
1.
内容:电路中感应电动势的大小,跟穿过这一电路的磁通量变化率
ΔΦ/Δ
t
成正比。
电磁感应定律:
2.
表达式:
(注意ΔΦ指的是磁通变化的绝对值)
ΔΦ/Δ
t
磁通量的变化率,反映磁通量变化的快慢。
Φ=(2+3t)
Wb
o
Φ
t
Φ-t图像中某点的切线的斜率、Φ-t函数中的k都表示磁通量的变化率
(1)S不变、B变化:
o
B
t
B=(2+3t)
T
B-t图像中某点的切线的斜率、B-t函数中的k都表示磁感应强度的变化率
例1:一个面积S=4×10-2m2、匝数n=100匝的线圈,放在匀强磁场中,磁场方向垂直于线圈平面,磁感应强度B的大小随时间变化的规律如图所示,由图可知(
)
A.在开始的2
s内穿过线圈的磁通量变化率为8
Wb/s
B.在开始的2s内穿过线圈的磁通量变化量等于零
C.在开始的2
s内线圈中产生的感应电动势等于8
V
D.在第3
s末的感应电动势为零
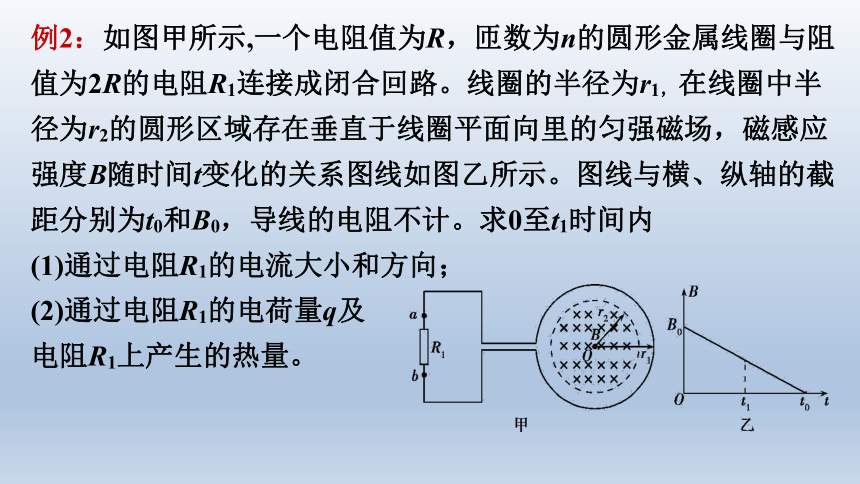
例2:如图甲所示,一个电阻值为R,匝数为n的圆形金属线圈与阻值为2R的电阻R1连接成闭合回路。线圈的半径为r1,在线圈中半径为r2的圆形区域存在垂直于线圈平面向里的匀强磁场,磁感应强度B随时间t变化的关系图线如图乙所示。图线与横、纵轴的截距分别为t0和B0,导线的电阻不计。求0至t1时间内
(1)通过电阻R1的电流大小和方向;
(2)通过电阻R1的电荷量q及
电阻R1上产生的热量。
应用电磁感应定律应注意的三个问题
(1)
指的是平均感应电动势,若磁通量均匀变化时,瞬时值等于平均值;
中的S为线圈在磁场范围内的有效面积;
(3)
电荷量q仅与n、ΔΦ和回路电阻R有关,与时间长短无关。
(2)B不变、S变化:
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
v
L
举例:如图所示,导体棒在外力的作用下,以速度v在宽度为L的导轨匀速运动,磁场的磁感应强度为B,试根据电磁感应定律推导其感应电动势的表达式,并且归纳其适用的条件。
导体棒扫过的面积
L、v指的是两两垂直时的速度和长度
在电路中使用E=BLv时,需注意:
(1)v必须是垂直于磁场、导体棒的速度;
(2)L必须是接入电路中的有效长度,且与速度、磁场垂直。
例4:有一个匀强磁场边界是EF,在EF右侧无磁场,左侧是匀强磁场区域,如图甲所示。现有一个闭合的金属线框以恒定速度从EF右侧水平进入匀强磁场区域。线框中的电流随时间变化的i-t图象如图乙所示,则
可能的线框是下列四个选
项中的( )
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
v
L
举例:如图所示,宽度为L的导轨以初速度v往右运动s后停下来,磁场的磁感应强度为B,试找找其隐藏的功能关系。
例5:如图所示,质量m1=0.1
kg,电阻R1=0.3
Ω,长度l=0.4
m的导体棒ab横放在U型金属框架上。框架质量m2=0.2
kg,放在绝缘水平面上,与水平面间的动摩擦因数μ=0.2.相距0.4
m的MM′、NN′相互平行,电阻不计且足够长。电阻R2=0.1
Ω的MN垂直于MM′。整个装置处于竖直向上的匀强磁场中,磁感应强度B=0.5
T。垂直于ab施加F=2
N的水平恒力,ab从静止开始无摩擦地运动,始终与MM′、NN′保持良好接触。当ab运动到某处时,框架开始运动。设框架与水平面间最大静摩擦力等于滑动摩擦力,g取10
m/s2.
(1)求框架开始运动时ab速度v的大小;
(2)从ab开始运动到框架开始运动的过程中,MN上产生的热量Q=0.1
J,求该过程ab位移x的大小。
举例:如图所示,导体棒在外力的作用下,宽度为L的导体棒以角速度
顺时针转动,磁场的磁感应强度为B,试根据电磁感应定律推导其感应电动势的表达式,并思考若以导体的中点顺时针转动时,其感应电动势又是多少?
E=Bl2ω,适用:匀强磁场、绕某一个端
点垂直切割磁感线产生的感应电动势。若
转轴不是端点,需根据两个电源的两个电
动势的大小和方向判断大小和方向。
例6:如图所示,一个转轮共有5根辐条,每根长皆为L,电阻皆为r,转轮的电阻不计,将它放在磁感应强度为B的匀强磁场里,磁场的方向垂直于轮面。A是轮轴,P为一与转轮边缘接触的触片,在轮子绕轴转动时P不动。在A、P间接一个电阻R,当轮以角速度ω绕轴做匀速转动时,流过R的电流等于________。
例7:(2016全国卷Ⅱ)(多选)法拉第圆盘发电机的示意图如图所示。铜圆盘安装在竖直的铜轴上,两铜片P、Q分别与圆盘的边缘和铜轴接触。圆盘处于方向竖直向上的匀强磁场B中。圆盘旋转时,关于流过电阻R的电流,下列说法正确的是( )
A.若圆盘转动的角速度恒定,则电流大小恒定
B.若从上向下看,圆盘顺时针转动,则电流沿a到b的方向流动
C.若圆盘转动方向不变,角速度大小发生变
化,则电流方向可能发生变化
D.若圆盘转动的角速度变为原来的2倍,则
电流在R上的热功率也变为原来的2倍
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
D
C
f
v
B增大
I
一、感生电动势:由于磁场发生变化产生的电动势
非静电力做功:变化磁场形成的电场
二、动生电动势:由于运动时切割磁感线产生的电动势
(平动切割)
(转动切割)
非静电力做功:洛伦兹力的分力
例8:如图所示,匀强磁场中有一矩形闭合线圈abcd,线圈平面与磁场垂直。已知线圈的匝数N=100,边长ab=1.0
m、bc=0.5
m,电阻r=2
Ω。磁感应强度B在0~1
s内从零均匀变化到0.2
T.在1~5
s内从0.2
T均匀变化到-0.2
T,取垂直纸面向里为磁场的正方向。求:
(1)0.5
s时线圈内感应电动势的大小E和感应电流的方向;
(2)在1~5
s内通过线圈的电荷量q;
(3)在0~5
s内线圈产生的焦耳热Q。
例9:如图甲所示,光滑导轨宽0.4
m,ab为金属棒,均匀变化的磁场垂直穿过导轨平面,磁场的变化情况如图乙所示,金属棒ab的电阻为1
Ω,导轨电阻不计。t=0时刻,ab棒从导轨最左端,以v=1
m/s的速度向右匀速运动,求:
(1)1s内回路中的平均感应电流;
(2)1
s末回路中的感应电流及金属
棒ab受到的安培力。
例10:如图所示,固定在匀强磁场中的水平“U形”导轨ab、cd的间距L1=0.5
m,ab与cd平行,金属棒垂直于ab且和ab、cd接触良好,金属棒与导轨左端bc的距离为L2=0.8
m,整个闭合回路的电阻为R=0.2
Ω,磁感应强度为B0=1
T的匀强磁场竖直向下穿过整个回路。ad通过滑轮和轻绳连接着一个质量为m=0.04
kg的物体,不计一切摩擦,现使磁场以0.2
T/s的变化率均匀地增大。求:
(1)金属棒上电流的方向。
(2)感应电动势的大小。
(3)物体刚好离开地面的时间(g取10
m/s2)。
例11:如图所示,半径为R、单位长度电阻为λ的均匀导体圆环固定在水平面上,圆环中心为O。匀强磁场垂直纸面方向向内,磁感应强度为B。平行于直径MON的导体杆,沿垂直于杆的方向向右运动。杆的电阻杆的电阻可以忽略不计,杆与圆环接触良好。某时刻,杆的位置如图,∠aob=2θ,速度为v。求此时刻作用在杆上安培力的大小和方向。
例12:如图所示,在水平面内固定着U形光滑金属导轨,轨道间距为50
cm,金属导体棒ab质量为0.1
kg,电阻为0.2Ω,横放在导轨上,电阻R的阻值是0.8
Ω(导轨其余部分电阻不计)。现加上竖直向下的磁感应强度为0.2
T的匀强磁场.用水平向右的恒力F=0.1
N拉动ab,使其从静止开始运动,则
(
)
A.导体棒ab开始运动后,电阻R中的电流方向是从P流向M
B.导体棒ab运动的最大速度为10
m/s
C.导体棒ab开始运动后,a、b两点的电势
差逐渐增加到1
V后保持不变
D.导体棒ab开始运动后任一时刻,F的功率
总等于导体棒ab和电阻R的发热功率之和
例13:如图所示,两足够长平行光滑的金属导轨
MN
、
PQ
相距为
L=1m
,导轨平面与水平面夹角θ=
30°,导轨上端跨接一定值电阻
R=2?,导轨电阻不计。整个装置处于方向垂直于导轨平面向上的匀强磁场
B
中,长为
L
的金属棒
ab
垂直于
MN
、
PQ
放置在导轨上,且与导轨保持电接触良好,金属棒的质量为
m=1kg
、电阻为
r=2?,现将金属棒由静止释放,当金属棒沿导轨下滑距离为
s=6m
时,速度达到最大值
v=5m/s
。g=10m/s
2,求:
(1)匀强磁场的磁感应强度
B
的大小?
(2)金属棒沿导轨下滑距离为
s
的过
程中,电阻
R
上产生的电热?
例14:如图所示,足够长的光滑平行金属导轨MN、PQ竖直放置,一匀强磁场垂直穿过导轨平面,导轨的上端M与P间连接阻值为R=0.40
Ω的电阻,质量为m=0.01
kg、电阻为r=0.30
Ω的金属棒ab紧贴在导轨上。现使金属棒ab由静止开始下滑,其下滑距离与时间的关系如下表所示,导轨电阻不计,g=10
m/s2。试求:
(1)当t=0.7
s时,重力对金属棒ab做功的功率;
(2)金属棒ab在开始运动的0.7
s内,
电阻R上产生的焦耳热;
(3)从开始运动到t=0.4
s的时间内,通过金属棒ab的电荷量。
时间t(s)
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
下滑距离s(m)
0
0.1
0.3
0.7
1.4
2.1
2.8
3.5
第十一章
电磁感应
法拉第电磁感应定律
G
E
r
a
b
G
E
r
a
b
G
a
b
G
a
b
认识感应电路问题:
1.
在电磁感应现象中产生的电动势称感应电动势。
2.产生感应电动势的那部分导体相当于电源。
3.产生感应电动势只需要磁通量发生变化,不需要闭合回路;
产生感应电流才需要磁通量发生变化和闭合回路。
4.区分电动势与路端电压的区别:路端电压指的是外电路的电压,只有开路时,路端电压才等于电动势。
5.感应电动势的正负极可以根据楞次定律来判断。
感应电动势的大小跟哪些因素有关呢?
从条件上看
从结果上看
相同
不同
Φ
变化的快慢不同
线圈的匝数不一样
Φ
都发生了变化
都产生了
I
产生的
I
大小不等
1.
内容:电路中感应电动势的大小,跟穿过这一电路的磁通量变化率
ΔΦ/Δ
t
成正比。
电磁感应定律:
2.
表达式:
(注意ΔΦ指的是磁通变化的绝对值)
ΔΦ/Δ
t
磁通量的变化率,反映磁通量变化的快慢。
Φ=(2+3t)
Wb
o
Φ
t
Φ-t图像中某点的切线的斜率、Φ-t函数中的k都表示磁通量的变化率
(1)S不变、B变化:
o
B
t
B=(2+3t)
T
B-t图像中某点的切线的斜率、B-t函数中的k都表示磁感应强度的变化率
例1:一个面积S=4×10-2m2、匝数n=100匝的线圈,放在匀强磁场中,磁场方向垂直于线圈平面,磁感应强度B的大小随时间变化的规律如图所示,由图可知(
)
A.在开始的2
s内穿过线圈的磁通量变化率为8
Wb/s
B.在开始的2s内穿过线圈的磁通量变化量等于零
C.在开始的2
s内线圈中产生的感应电动势等于8
V
D.在第3
s末的感应电动势为零
例2:如图甲所示,一个电阻值为R,匝数为n的圆形金属线圈与阻值为2R的电阻R1连接成闭合回路。线圈的半径为r1,在线圈中半径为r2的圆形区域存在垂直于线圈平面向里的匀强磁场,磁感应强度B随时间t变化的关系图线如图乙所示。图线与横、纵轴的截距分别为t0和B0,导线的电阻不计。求0至t1时间内
(1)通过电阻R1的电流大小和方向;
(2)通过电阻R1的电荷量q及
电阻R1上产生的热量。
应用电磁感应定律应注意的三个问题
(1)
指的是平均感应电动势,若磁通量均匀变化时,瞬时值等于平均值;
中的S为线圈在磁场范围内的有效面积;
(3)
电荷量q仅与n、ΔΦ和回路电阻R有关,与时间长短无关。
(2)B不变、S变化:
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
v
L
举例:如图所示,导体棒在外力的作用下,以速度v在宽度为L的导轨匀速运动,磁场的磁感应强度为B,试根据电磁感应定律推导其感应电动势的表达式,并且归纳其适用的条件。
导体棒扫过的面积
L、v指的是两两垂直时的速度和长度
在电路中使用E=BLv时,需注意:
(1)v必须是垂直于磁场、导体棒的速度;
(2)L必须是接入电路中的有效长度,且与速度、磁场垂直。
例4:有一个匀强磁场边界是EF,在EF右侧无磁场,左侧是匀强磁场区域,如图甲所示。现有一个闭合的金属线框以恒定速度从EF右侧水平进入匀强磁场区域。线框中的电流随时间变化的i-t图象如图乙所示,则
可能的线框是下列四个选
项中的( )
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
v
L
举例:如图所示,宽度为L的导轨以初速度v往右运动s后停下来,磁场的磁感应强度为B,试找找其隐藏的功能关系。
例5:如图所示,质量m1=0.1
kg,电阻R1=0.3
Ω,长度l=0.4
m的导体棒ab横放在U型金属框架上。框架质量m2=0.2
kg,放在绝缘水平面上,与水平面间的动摩擦因数μ=0.2.相距0.4
m的MM′、NN′相互平行,电阻不计且足够长。电阻R2=0.1
Ω的MN垂直于MM′。整个装置处于竖直向上的匀强磁场中,磁感应强度B=0.5
T。垂直于ab施加F=2
N的水平恒力,ab从静止开始无摩擦地运动,始终与MM′、NN′保持良好接触。当ab运动到某处时,框架开始运动。设框架与水平面间最大静摩擦力等于滑动摩擦力,g取10
m/s2.
(1)求框架开始运动时ab速度v的大小;
(2)从ab开始运动到框架开始运动的过程中,MN上产生的热量Q=0.1
J,求该过程ab位移x的大小。
举例:如图所示,导体棒在外力的作用下,宽度为L的导体棒以角速度
顺时针转动,磁场的磁感应强度为B,试根据电磁感应定律推导其感应电动势的表达式,并思考若以导体的中点顺时针转动时,其感应电动势又是多少?
E=Bl2ω,适用:匀强磁场、绕某一个端
点垂直切割磁感线产生的感应电动势。若
转轴不是端点,需根据两个电源的两个电
动势的大小和方向判断大小和方向。
例6:如图所示,一个转轮共有5根辐条,每根长皆为L,电阻皆为r,转轮的电阻不计,将它放在磁感应强度为B的匀强磁场里,磁场的方向垂直于轮面。A是轮轴,P为一与转轮边缘接触的触片,在轮子绕轴转动时P不动。在A、P间接一个电阻R,当轮以角速度ω绕轴做匀速转动时,流过R的电流等于________。
例7:(2016全国卷Ⅱ)(多选)法拉第圆盘发电机的示意图如图所示。铜圆盘安装在竖直的铜轴上,两铜片P、Q分别与圆盘的边缘和铜轴接触。圆盘处于方向竖直向上的匀强磁场B中。圆盘旋转时,关于流过电阻R的电流,下列说法正确的是( )
A.若圆盘转动的角速度恒定,则电流大小恒定
B.若从上向下看,圆盘顺时针转动,则电流沿a到b的方向流动
C.若圆盘转动方向不变,角速度大小发生变
化,则电流方向可能发生变化
D.若圆盘转动的角速度变为原来的2倍,则
电流在R上的热功率也变为原来的2倍
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
×
D
C
f
v
B增大
I
一、感生电动势:由于磁场发生变化产生的电动势
非静电力做功:变化磁场形成的电场
二、动生电动势:由于运动时切割磁感线产生的电动势
(平动切割)
(转动切割)
非静电力做功:洛伦兹力的分力
例8:如图所示,匀强磁场中有一矩形闭合线圈abcd,线圈平面与磁场垂直。已知线圈的匝数N=100,边长ab=1.0
m、bc=0.5
m,电阻r=2
Ω。磁感应强度B在0~1
s内从零均匀变化到0.2
T.在1~5
s内从0.2
T均匀变化到-0.2
T,取垂直纸面向里为磁场的正方向。求:
(1)0.5
s时线圈内感应电动势的大小E和感应电流的方向;
(2)在1~5
s内通过线圈的电荷量q;
(3)在0~5
s内线圈产生的焦耳热Q。
例9:如图甲所示,光滑导轨宽0.4
m,ab为金属棒,均匀变化的磁场垂直穿过导轨平面,磁场的变化情况如图乙所示,金属棒ab的电阻为1
Ω,导轨电阻不计。t=0时刻,ab棒从导轨最左端,以v=1
m/s的速度向右匀速运动,求:
(1)1s内回路中的平均感应电流;
(2)1
s末回路中的感应电流及金属
棒ab受到的安培力。
例10:如图所示,固定在匀强磁场中的水平“U形”导轨ab、cd的间距L1=0.5
m,ab与cd平行,金属棒垂直于ab且和ab、cd接触良好,金属棒与导轨左端bc的距离为L2=0.8
m,整个闭合回路的电阻为R=0.2
Ω,磁感应强度为B0=1
T的匀强磁场竖直向下穿过整个回路。ad通过滑轮和轻绳连接着一个质量为m=0.04
kg的物体,不计一切摩擦,现使磁场以0.2
T/s的变化率均匀地增大。求:
(1)金属棒上电流的方向。
(2)感应电动势的大小。
(3)物体刚好离开地面的时间(g取10
m/s2)。
例11:如图所示,半径为R、单位长度电阻为λ的均匀导体圆环固定在水平面上,圆环中心为O。匀强磁场垂直纸面方向向内,磁感应强度为B。平行于直径MON的导体杆,沿垂直于杆的方向向右运动。杆的电阻杆的电阻可以忽略不计,杆与圆环接触良好。某时刻,杆的位置如图,∠aob=2θ,速度为v。求此时刻作用在杆上安培力的大小和方向。
例12:如图所示,在水平面内固定着U形光滑金属导轨,轨道间距为50
cm,金属导体棒ab质量为0.1
kg,电阻为0.2Ω,横放在导轨上,电阻R的阻值是0.8
Ω(导轨其余部分电阻不计)。现加上竖直向下的磁感应强度为0.2
T的匀强磁场.用水平向右的恒力F=0.1
N拉动ab,使其从静止开始运动,则
(
)
A.导体棒ab开始运动后,电阻R中的电流方向是从P流向M
B.导体棒ab运动的最大速度为10
m/s
C.导体棒ab开始运动后,a、b两点的电势
差逐渐增加到1
V后保持不变
D.导体棒ab开始运动后任一时刻,F的功率
总等于导体棒ab和电阻R的发热功率之和
例13:如图所示,两足够长平行光滑的金属导轨
MN
、
PQ
相距为
L=1m
,导轨平面与水平面夹角θ=
30°,导轨上端跨接一定值电阻
R=2?,导轨电阻不计。整个装置处于方向垂直于导轨平面向上的匀强磁场
B
中,长为
L
的金属棒
ab
垂直于
MN
、
PQ
放置在导轨上,且与导轨保持电接触良好,金属棒的质量为
m=1kg
、电阻为
r=2?,现将金属棒由静止释放,当金属棒沿导轨下滑距离为
s=6m
时,速度达到最大值
v=5m/s
。g=10m/s
2,求:
(1)匀强磁场的磁感应强度
B
的大小?
(2)金属棒沿导轨下滑距离为
s
的过
程中,电阻
R
上产生的电热?
例14:如图所示,足够长的光滑平行金属导轨MN、PQ竖直放置,一匀强磁场垂直穿过导轨平面,导轨的上端M与P间连接阻值为R=0.40
Ω的电阻,质量为m=0.01
kg、电阻为r=0.30
Ω的金属棒ab紧贴在导轨上。现使金属棒ab由静止开始下滑,其下滑距离与时间的关系如下表所示,导轨电阻不计,g=10
m/s2。试求:
(1)当t=0.7
s时,重力对金属棒ab做功的功率;
(2)金属棒ab在开始运动的0.7
s内,
电阻R上产生的焦耳热;
(3)从开始运动到t=0.4
s的时间内,通过金属棒ab的电荷量。
时间t(s)
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
下滑距离s(m)
0
0.1
0.3
0.7
1.4
2.1
2.8
3.5
