人教版八年级数学上册第十二章全等三角形复习讲义教师版
文档属性
| 名称 | 人教版八年级数学上册第十二章全等三角形复习讲义教师版 |  | |
| 格式 | zip | ||
| 文件大小 | 288.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 08:29:06 | ||
图片预览




文档简介
学习目标
正确理解全等的概念,能够识别全等图形;
能够准确找到全等的对应边、对应角,会进行全等三角形的表示;
能够利用全等三角形的性质进行相关的计算.
重难点分析
全等三角形对应边、对应角的识别;
全等三角形的性质及其相关计算.
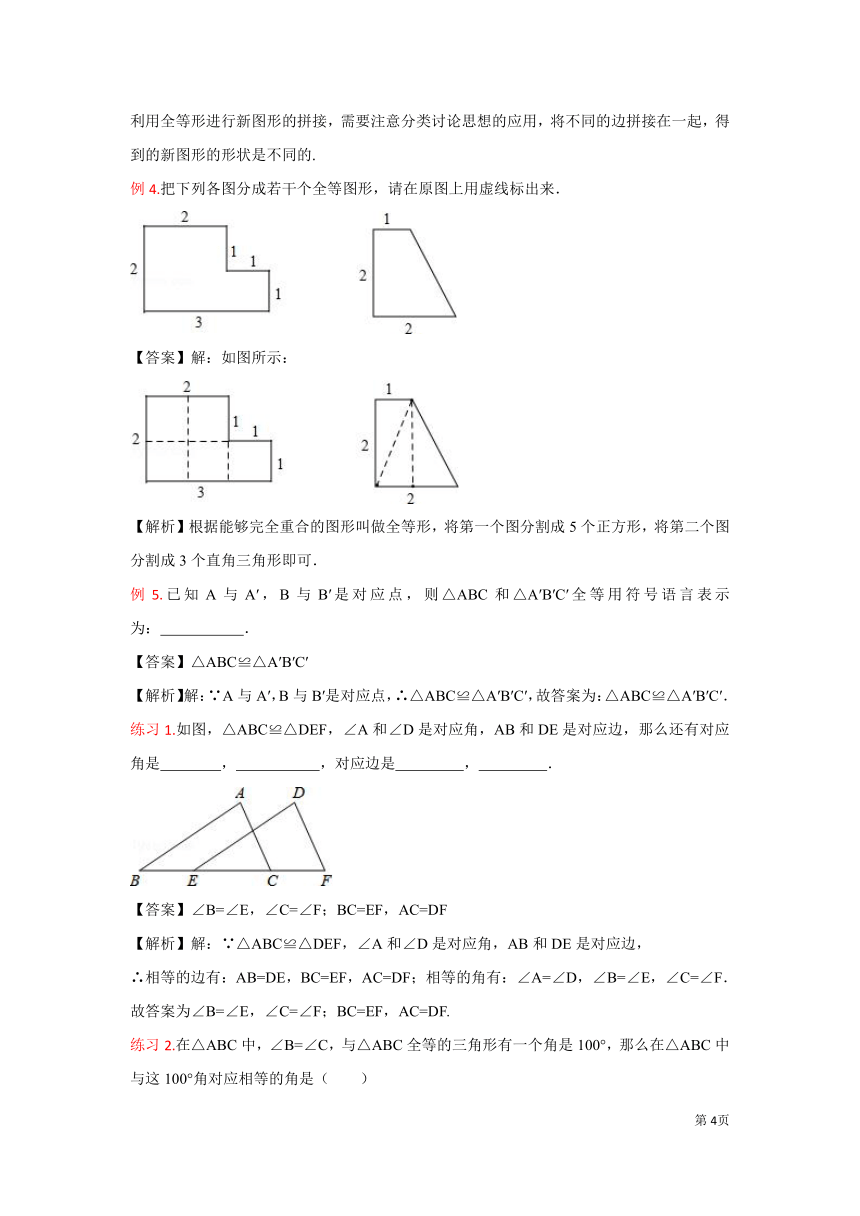
要点集结
精讲精练
全等的概念及其表示
1、全等形的概念:能够完全重合的两个图形叫做全等形.
2、全等三角形的概念:能够完全重合的两个三角形叫做全等三角形.
3、全等的符号表示:“全等”用符号“≌”表示.
注意:在记两个三角形全等时,通常把对应顶点写在对应位置上.
4、全等的对应顶点、对应边、对应角
(1)把两个全等三角形重合到一起,重合的顶点叫做对应顶点;
(2)把两个全等三角形重合到一起,重合的边叫做对应边;
(3)把两个全等三角形重合到一起,重合的角叫做对应角.
例1.下列图形中与已知图形全等的是( )
A.
B.
C.
D.
【答案】B
练习1.下列选项中,和下图全等的图形是( )
A.
B.
C.
D.
【答案】D
练习2.下列图形中,是由多个全等图形组成的图案的是( )
A.
B.
C.
D.
【答案】C
小结
根据全等的定义识别全等的图形,图形全等的本质就是经过移动后能够完全重合.
例2.下列说法正确的是( )
A.面积相等的两个长方形全等
B.周长相等的两个长方形全等
C.形状相同的两个长方形全等
D.能够完全重合的两个长方形全等
【答案】D
【解析】解:根据能够完全重合的两个图形是全等图形可知,
能够完全重合的两个长方形全等,面积相等,周长相等,形状相同,都不一定能够完全重合.
所以A、B、C选项不一定正确,D选项一定正确.故选D.
练习1.下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
【答案】C
【解析】解:A、形状相同的两个三角形全等,说法错误,应该是形状相同且大小也相同的两个三角形全等;
B、面积相等的两个三角形全等,说法错误;
C、完全重合的两个三角形全等,说法正确;
D、所有的等边三角形全等,说法错误;
小结
利用语言描述图形的特征,再根据特征进行全等的判别,此类问题较直接看图辨别的类型难度要稍大一些,需要学生对所描述的图形的几何性质要相对熟悉一些,并能够根据几何性质去判断图形的具体形状是否可以固定,从而判断是否全等.
例3.用两个全等的三角形一定不能拼出的图形是( )
A.等腰三角形
B.直角梯形
C.菱形
D.矩形
【答案】B
【解析】解:用两个全等的直角三角形就能拼出等腰三角形,A可以;
如图两个全等的正三角形就可以拼出菱形,C可以;
两个全等的直角三角形时就可以拼出矩形,D可以;
不管用什么形状的两个全等的三角形不管怎样也拼不出直角梯形.
故选B.
小结
利用全等形进行新图形的拼接,需要注意分类讨论思想的应用,将不同的边拼接在一起,得到的新图形的形状是不同的.
例4.把下列各图分成若干个全等图形,请在原图上用虚线标出来.
【答案】解:如图所示:
【解析】根据能够完全重合的图形叫做全等形,将第一个图分割成5个正方形,将第二个图分割成3个直角三角形即可.
例5.已知A与A′,B与B′是对应点,则△ABC和△A′B′C′全等用符号语言表示为:
.
【答案】△ABC≌△A′B′C′
【解析】解:∵A与A′,B与B′是对应点,∴△ABC≌△A′B′C′,故答案为:△ABC≌△A′B′C′.
练习1.如图,△ABC≌△DEF,∠A和∠D是对应角,AB和DE是对应边,那么还有对应角是
,
,对应边是
,
.
【答案】∠B=∠E,∠C=∠F;BC=EF,AC=DF
【解析】解:∵△ABC≌△DEF,∠A和∠D是对应角,AB和DE是对应边,
∴相等的边有:AB=DE,BC=EF,AC=DF;相等的角有:∠A=∠D,∠B=∠E,∠C=∠F.
故答案为∠B=∠E,∠C=∠F;BC=EF,AC=DF.
练习2.在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中与这100°角对应相等的角是( )
A.∠A
B.∠B
C.∠C
D.∠B或∠C
【答案】A
【解析】解:在△ABC中,∵∠B=∠C,∴∠B、∠C不能等于100°,
∴与△ABC全等的三角形的100°的角的对应角是∠A.故选:A.
小结
在用全等符号表示两三角形全等时,一定要注意将对应的点写在对应的位置上,这样方便找到对应边和对应角.在最开始学的时候就养成这样的好习惯,是非常有必要的.
全等的性质及其相关计算
1、全等三角形的性质
性质1:全等三角形的对应边相等
性质2:全等三角形的对应角相等
注意:
(1)全等三角形的对应边上的高、中线以及对应角的平分线相等;
(2)全等三角形的周长相等,面积相等;
(3)平移、翻折、旋转前后的图形全等.
2、关于全等三角形的性质应注意
(1)全等三角形的性质是证明线段和角相等的理论依据,应用时要会找对应角和对应边;
(2)要正确区分对应边与对边,对应角与对角的概念
对应边、对应角是对两个三角形而言,而对边、对角是对同一个三角形的边和角而言的,对边是指同一个三角形中角的对边,对角是指同一个三角形中边的对角.
例1.如图,已知△ABC≌△DEB,点E在AB上,若DE=8,BC=5,线AE的长为( )
A.3
B.5
C.6
D.4
【答案】A
【解析】解:∵△ABC≌△DEB,∴AB=DE=8,BE=BC=5,
∴AE=AB﹣BE=3,故选:A.
练习1.如图,已知△ABC≌△DAE,BC=2,DE=5,则CE的长为( )
A.2
B.2.5
C.3
D.3.5
【答案】C
【解析】解:∵△ABC≌△DAE,∴AC=DE=5,BC=AE=2,∴CE=5﹣2=3.故选C.
练习2.下列说法错误的是( )
A.全等三角形对应边上的中线相等
B.面积相等的两个三角形是全等三角形
C.全等三角形对应边上的高相等
D.全等三角形对应角平分线相等
【答案】B
小结
全等的一个典型性质就是对应边相等,所以在有全等形的求线段长度的题目中,一定要注意对全等对应边相等这一性质的应用.同时对于两个全等的三角形来说,不仅对应边相等,对应的角平分线、中线、高线也分别是相等的,这就为全等形中计算线段的长度提供了又一个理论依据.
例2.如图,在△ABC中,D、E分别是AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数是( )
A.15°
B.20°
C.25°
D.30°
【答案】D
【解析】解:∵△ADB≌△EDB≌△EDC,∴AB=BE=EC,∠ABD=∠DBE=∠C,
∴∠A=90°,∴∠C=30°,故选:D.
练习1.如图,两个三角形为全等三角形,则∠α的度数是( )
A.72°
B.60°
C.58°
D.50°
【答案】A
【解析】解:根据三角形内角和可得∠1=180°﹣50°﹣58°=72°,
因为两个全等三角形,所以∠α=∠1=72°,故选A.
小结
全等的另一个典型性质是对应角相等,在全等形存在的题目中进行角度计算时,一定要注意对这一性质的应用.
全等性质中常见模型的识别
在利用全等三角形的性质进行相关的边、角计算时,除了直接利用性质外,还需要对一些常见的几何结构能够准确识别,从而逐步建立几何感知能力.如:
平移型:
旋转型
翻折型
对调性型
共角型
共边型——其本质也是翻折型
一线三等角之三垂直模型
例1.如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求角F的度数与DH的长;
(2)求证:AB∥DE.
【答案】解:(1)∵∠A=85°,∠B=60°,∴∠ACB=180°﹣∠A﹣∠B=35°,
∵△ABC≌△DEF,AB=8,∴∠F=∠ACB=35°,DE=AB=8,
∵EH=2,∴DH=8﹣2=6;
(2)证明:∵△ABC≌△DEF,∴∠DEF=∠B,∴AB∥DE.
【解析】(1)根据三角形内角和定理求出∠ACB,根据全等三角形的性质得出AB=DE,∠F=∠ACB,即可得出答案;(2)根据全等三角形的性质得出∠B=∠DEF,根据平行线的判定得出即可.
练习1.如图,△ABC≌△DEF,AC∥DF,则∠C的对应角为( )
A.∠F
B.∠AGE
C.∠AEF
D.∠D
【答案】A
【解析】解:∵AC∥DF,∴∠D=∠BAC;
∵△ABC≌△DEF,∴△ABC与△DEF的对应角相等;
又∠C是△ABC的一个内角,∴∠C的对应角应△DEF的一个内角;
A、∠AGE不是△DEF的一个内角,不符合题意;
B、∠AEF不是△DEF的一个内角,不符合题意;
C、∠D与∠BAC是对应角,不符合题意;
故选A.
小结
注意平移型全等形的识别,平移的距离可以有多种情况,两个图形可以没有公共的部分,这也是平移型的一种典型情况,在授课过程中注意帮助学生建立这种模型意识.
例2.已知:如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:∵△ABC≌△AEF,∴AC=AF,故①正确;
∠EAF=∠BAC,∴∠FAC=∠EAB≠∠FAB,故②错误;
EF=BC,故③正确;
∠EAB=∠FAC,故④正确;
综上所述,结论正确的是①③④共3个.故选C.
练习1.如图,△ABC≌△DBE,∠DBC=150°,∠ABD=40°,则∠ABE的度数是( )
A.70°
B.65°
C.60°
D.55°
【答案】A
【解析】解:∵∠DBC=150°,∠ABD=40°,∴∠ABC=110°,
∵△ABC≌△DBE,∴∠DBE=∠ABC=110°,∴∠ABE=∠DBE﹣∠ABD=70°,故选:A.
小结
注意旋转型全等形的识别,旋转的角度也可以有很多种,两个图形可以没有公共的部分,这也是旋转的一种典型情况,在授课过程中注意帮助学生建立这种模型意识.
例3.如图,已知△ABC≌△DCB,AB=10,∠A=60°,∠ABC=80°,那么下列结论中错误的是( )
A.∠D=60°
B.∠DBC=40°
C.AC=DB
D.BE=10
【答案】D
【解析】解:∵∠A=60°,∠ABC=80°,∴∠ACB=40°,
∵△ABC≌△DCB,∴∠D=∠A=60°,∠DBC=∠ACB=40°,AC=BD,
故A,B,C正确,故选D.
练习1.如图,点E,F在线段BC上,△ABF与△DEC全等,其中点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DEC等于( )
A.∠B
B.∠A
C.∠EMF
D.∠AFB
【答案】D
【解析】解:∵△ABF与△DEC全等,点A与点D,点B与点C是对应顶点,
∴△ABF≌△DCE,∴∠DEC=∠AFB,故选:D.
小结
注意翻折型全等形的识别,翻折的本质是轴对称,其中轴对称的知识会在下一章中学到,其中对称轴的位置决定了翻折前后形成的两个图形的位置关系,建议老师在讲解旋转、翻折、平移这三个模型时,要以动态的思想来分析、帮助学生理解不同的形式产生的原因,在授课过程中注意帮助学生建立这种模型意识.
例4.如图,△ABD≌△CDB,下面四个结论中不正确的是( )
A.△ABD和△CDB的面积相等
B.△ABD和△CDB的周长相等
C.∠A+∠ABD=∠C+∠CBD
D.AD∥BC,且AD=BC
【答案】C
【解析】解:∵△ABD≌△CDB,
∴∠ADB=∠CBD,AD=BC,△ABD和△CDB的面积相等,△ABD和△CDB的周长相等,
∴AD∥BC,则选项A,B,D一定正确.
由△ABD≌△CDB不一定能得到∠ABD=∠CBD,
因而∠A+∠ABD=∠C+∠CBD不一定成立.故选C.
练习1.如图,△ABC≌△BAD,若AB=6、AC=4、BC=5,则△BAD的周长为 .
【答案】15
【解析】解:∵△ABC≌△BAD,∴AD=CB=5,BD=AC=4,
∵AB=6,∴△BAD的周长为:5+4+6=15,故答案为:15.
小结
对调型的全等也有不同的位置、不同的情况,其中有一条边完全重合的情况构成的是平行四边形(在人教版初二下学期的课本中会学到),对于这种类型的全等,一定要注意区分其对应点和对应边分别是什么.
例5.如图:若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
A.2
B.3
C.5
D.2.5
【答案】B
【解析】解:∵△ABE≌△ACF,AB=5,∴AC=AB=5,
∵AE=2,∴EC=AC﹣AE=5﹣2=3,故选B.
练习1.如图,△ABE≌△ACF.若AB=5,AE=2,BE=4,则CF的长度是( )
A.2
B.5
C.4
D.3
【答案】C
【解析】解:∵△ABE≌△ACF,∴CF=BE=4,故选:C.
练习2.已知如图,△OAD≌△OBC,且∠O=70°,∠C=25°,则∠OAD=( )
A.95°
B.85°
C.75°
D.65°
【答案】B
【解析】解:∵△OAD≌△OBC,∴∠D=∠C=25°,
∵∠O=70°,∴∠OAD=180°﹣25°﹣70°=85°,故选:B.
小结
共角模型其本质也是翻折的一种,由于它有一个公共角,其情况比较特殊,所以单独拿出来分析,此种模型在下一节的全等判定中出现的频率很高,其中蕴藏着两组全等三角形,两者之间的转化很经典.
例6.如图,△ABC≌△DCB,若AC=7,BE=5,则DE的长为( )
A.2
B.3
C.4
D.5
【答案】A
【解析】解:∵△ABC≌△DCB,∴BD=AC=7,∵BE=5,∴DE=BD﹣BE=2,故选A.
练习1.如图,已知△ABC≌△BAD,A和B,C和D分别是对应顶点,且∠C=60°,∠ABD=35°,则∠BAD的度数是( )
A.60°
B.35°
C.85°
D.不能确定
【答案】C
【解析】解:∵△ABC≌△BAD,∠C=60°,∴∠D=∠C=60°,
∵∠ABD=35°,∴∠BAD=180°﹣∠D﹣∠ABD=180°﹣60°﹣35°=85°,故选C.
小结
共边型全等其本质也是翻折型,是翻折的一个特殊情况.
例7.如图,E为线段AB上一点,AC⊥AB,DB⊥AB,△ACE≌△BED.
(1)试猜想线段CE与DE的位置关系,并证明你的结论;
(2)求证:AB=AC+BD.
【答案】(1)CE⊥DE,
证明:∵AC⊥AB,DB⊥AB,
∴∠A=∠B=90°,∴∠C+∠CEA=90°,
∵△ACE≌△BED,∴∠C=∠DEB,
∴∠CEA+∠DEB=90°,
∴∠CED=180°﹣90°=90°,∴CE⊥DE;
证明:∵△ACE≌△BED,
∴AC=BE,BD=AE,
∴AB=AE+BE=AC+BD.
【解析】(1)求出∠A=∠B=90°,推出∠C+∠CEA=90°,根据全等得出∠C=∠DEB,推出∠CEA+∠DEB=90°即可;(2)根据全等三角形的性质得出AC=BE,BD=AE,即可得出答案.
练习1.如图,已知Rt△ABC≌Rt△CDE,∠B=∠D=90°,且B,C,D三点共线.试说明∠ACE=90°.
【答案】证明:∵Rt△ABC≌Rt△CDE,∴∠BCA=∠CED,
∵△DCE是直角三角形,∴∠CED+∠ECD=90°,
∴∠BCA+∠ECD=90°,∴∠ACE=180°-90°=90°.
【解析】根据Rt△ABC≌Rt△CDE可得∠BCA=∠CED,再根据直角三角形两锐角互余可得∠CED+∠ECD=90°,进而得到∠BCA+∠ECD=90°,再根据角之间的关系可得∠ACE=90°.
小结
三垂直模型其本质也是一种旋转,由于其旋转中心不容易确定,所以将此类情况单独拿出来分析,而三垂直的更一般的情况是一线三等角,它是初三相似中非常重要的一个模型.
当堂总结
本次课重点讲解三角形全等的性质及其相关计算,其中需要学生特别关注的就是一些常见的全等的模型,这也为下一节讲解三角形全等的判定作铺垫,在学习全等三角形章节一定要着重关注常见的全等模型,这对计算和证明都有很好的帮助.
课后作业
1、如图,△ADE≌△BDE,若△ADC的周长为12,AC的长为5,则CB的长为( )
A.8
B.7
C.6
D.5
【答案】B
【解析】解:∵△ADE≌△BDE,∴DA=DB,
△ADC的周长=AC+CD+AD=AC+CD+BD=AC+BC=12,又AC=5,∴BC=7,故选:B.
2、若△ABC≌△DEF,且△ABC的周长为20,AB=5,BC=8,则DF长为( )
A.5
B.8
C.7
D.5或8
【答案】C
【解析】解:∵△ABC的周长为20,AB=5,BC=8,∴AC=20﹣5﹣8=7,
∵△ABC≌△DEF,∴DF=AC=7,故选:C.
3、如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( )
A.AB=AC
B.∠BAE=∠CAD
C.BE=DC
D.AD=DE
【答案】D
【解析】解:∵△ABE≌△ACD,∠1=∠2,∠B=∠C,
∴AB=AC,∠BAE=∠CAD,BE=DC,AD=AE,故A、B、C正确;
AD的对应边是AE而非DE,所以D错误.故选D.
4、如图,△ABD≌△ACE,点B和点C是对应顶点,AB=8,AD=6,BD=7,则CE的长是( )
A.1
B.2
C.4
D.7
【答案】D
【解析】解:∵△ABD≌△ACE,∴BD=CE=7.故选:D.
5、如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=42°,AB=9,AD=6,G为AB延长线上一点.
(1)求∠EBG的度数.
(2)求CE的长.
【答案】解:(1)∵△ABE≌△ACD,∴∠EBA=∠C=42°,∴∠EBG=180°﹣42°=138°;
(2)∵△ABE≌△ACD,∴AC=AB=9,AE=AD=6,∴CE=AC﹣AE=9﹣6=3.
6、如图所示,已知△ABC≌△DCB,∠A=32°,∠BCD=115°,求∠BOC.
【答案】解:∵△ABC≌△DCB,∴∠DBC=∠ACB,∠A=∠D,
△ABC中,∠A=32°,∴∠D=32°,∴∠DBC=∠ACB=180°﹣∠D﹣∠BCD=33°,
∴∠OBC=∠OCB=33°,∴∠BOC=180°﹣33°﹣33°=114°.
【解析】根据三角形内角和定理可求∠DBC=33°,根据全等三角形的性质可证∠DBC=∠ACB,即可求∠BOC.
7、如图,E为线段BC上一点,AB⊥BC,△ABE≌△ECD,判断AE与DE的关系,并证明你的结论.
【答案】解:AE⊥DE.
∵AB⊥BC,∴∠B=90°.
∵△ABE≌△ECD,∴∠A=∠DEC,∠AEB=∠EDC,∠B=∠C=90°.
∵∠A+∠AEB=90°,∠DEC+∠D=90°,∴∠AEB+∠DEC=90°,∴∠AED=90°,即AE⊥DE.
第4页
正确理解全等的概念,能够识别全等图形;
能够准确找到全等的对应边、对应角,会进行全等三角形的表示;
能够利用全等三角形的性质进行相关的计算.
重难点分析
全等三角形对应边、对应角的识别;
全等三角形的性质及其相关计算.
要点集结
精讲精练
全等的概念及其表示
1、全等形的概念:能够完全重合的两个图形叫做全等形.
2、全等三角形的概念:能够完全重合的两个三角形叫做全等三角形.
3、全等的符号表示:“全等”用符号“≌”表示.
注意:在记两个三角形全等时,通常把对应顶点写在对应位置上.
4、全等的对应顶点、对应边、对应角
(1)把两个全等三角形重合到一起,重合的顶点叫做对应顶点;
(2)把两个全等三角形重合到一起,重合的边叫做对应边;
(3)把两个全等三角形重合到一起,重合的角叫做对应角.
例1.下列图形中与已知图形全等的是( )
A.
B.
C.
D.
【答案】B
练习1.下列选项中,和下图全等的图形是( )
A.
B.
C.
D.
【答案】D
练习2.下列图形中,是由多个全等图形组成的图案的是( )
A.
B.
C.
D.
【答案】C
小结
根据全等的定义识别全等的图形,图形全等的本质就是经过移动后能够完全重合.
例2.下列说法正确的是( )
A.面积相等的两个长方形全等
B.周长相等的两个长方形全等
C.形状相同的两个长方形全等
D.能够完全重合的两个长方形全等
【答案】D
【解析】解:根据能够完全重合的两个图形是全等图形可知,
能够完全重合的两个长方形全等,面积相等,周长相等,形状相同,都不一定能够完全重合.
所以A、B、C选项不一定正确,D选项一定正确.故选D.
练习1.下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
【答案】C
【解析】解:A、形状相同的两个三角形全等,说法错误,应该是形状相同且大小也相同的两个三角形全等;
B、面积相等的两个三角形全等,说法错误;
C、完全重合的两个三角形全等,说法正确;
D、所有的等边三角形全等,说法错误;
小结
利用语言描述图形的特征,再根据特征进行全等的判别,此类问题较直接看图辨别的类型难度要稍大一些,需要学生对所描述的图形的几何性质要相对熟悉一些,并能够根据几何性质去判断图形的具体形状是否可以固定,从而判断是否全等.
例3.用两个全等的三角形一定不能拼出的图形是( )
A.等腰三角形
B.直角梯形
C.菱形
D.矩形
【答案】B
【解析】解:用两个全等的直角三角形就能拼出等腰三角形,A可以;
如图两个全等的正三角形就可以拼出菱形,C可以;
两个全等的直角三角形时就可以拼出矩形,D可以;
不管用什么形状的两个全等的三角形不管怎样也拼不出直角梯形.
故选B.
小结
利用全等形进行新图形的拼接,需要注意分类讨论思想的应用,将不同的边拼接在一起,得到的新图形的形状是不同的.
例4.把下列各图分成若干个全等图形,请在原图上用虚线标出来.
【答案】解:如图所示:
【解析】根据能够完全重合的图形叫做全等形,将第一个图分割成5个正方形,将第二个图分割成3个直角三角形即可.
例5.已知A与A′,B与B′是对应点,则△ABC和△A′B′C′全等用符号语言表示为:
.
【答案】△ABC≌△A′B′C′
【解析】解:∵A与A′,B与B′是对应点,∴△ABC≌△A′B′C′,故答案为:△ABC≌△A′B′C′.
练习1.如图,△ABC≌△DEF,∠A和∠D是对应角,AB和DE是对应边,那么还有对应角是
,
,对应边是
,
.
【答案】∠B=∠E,∠C=∠F;BC=EF,AC=DF
【解析】解:∵△ABC≌△DEF,∠A和∠D是对应角,AB和DE是对应边,
∴相等的边有:AB=DE,BC=EF,AC=DF;相等的角有:∠A=∠D,∠B=∠E,∠C=∠F.
故答案为∠B=∠E,∠C=∠F;BC=EF,AC=DF.
练习2.在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,那么在△ABC中与这100°角对应相等的角是( )
A.∠A
B.∠B
C.∠C
D.∠B或∠C
【答案】A
【解析】解:在△ABC中,∵∠B=∠C,∴∠B、∠C不能等于100°,
∴与△ABC全等的三角形的100°的角的对应角是∠A.故选:A.
小结
在用全等符号表示两三角形全等时,一定要注意将对应的点写在对应的位置上,这样方便找到对应边和对应角.在最开始学的时候就养成这样的好习惯,是非常有必要的.
全等的性质及其相关计算
1、全等三角形的性质
性质1:全等三角形的对应边相等
性质2:全等三角形的对应角相等
注意:
(1)全等三角形的对应边上的高、中线以及对应角的平分线相等;
(2)全等三角形的周长相等,面积相等;
(3)平移、翻折、旋转前后的图形全等.
2、关于全等三角形的性质应注意
(1)全等三角形的性质是证明线段和角相等的理论依据,应用时要会找对应角和对应边;
(2)要正确区分对应边与对边,对应角与对角的概念
对应边、对应角是对两个三角形而言,而对边、对角是对同一个三角形的边和角而言的,对边是指同一个三角形中角的对边,对角是指同一个三角形中边的对角.
例1.如图,已知△ABC≌△DEB,点E在AB上,若DE=8,BC=5,线AE的长为( )
A.3
B.5
C.6
D.4
【答案】A
【解析】解:∵△ABC≌△DEB,∴AB=DE=8,BE=BC=5,
∴AE=AB﹣BE=3,故选:A.
练习1.如图,已知△ABC≌△DAE,BC=2,DE=5,则CE的长为( )
A.2
B.2.5
C.3
D.3.5
【答案】C
【解析】解:∵△ABC≌△DAE,∴AC=DE=5,BC=AE=2,∴CE=5﹣2=3.故选C.
练习2.下列说法错误的是( )
A.全等三角形对应边上的中线相等
B.面积相等的两个三角形是全等三角形
C.全等三角形对应边上的高相等
D.全等三角形对应角平分线相等
【答案】B
小结
全等的一个典型性质就是对应边相等,所以在有全等形的求线段长度的题目中,一定要注意对全等对应边相等这一性质的应用.同时对于两个全等的三角形来说,不仅对应边相等,对应的角平分线、中线、高线也分别是相等的,这就为全等形中计算线段的长度提供了又一个理论依据.
例2.如图,在△ABC中,D、E分别是AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数是( )
A.15°
B.20°
C.25°
D.30°
【答案】D
【解析】解:∵△ADB≌△EDB≌△EDC,∴AB=BE=EC,∠ABD=∠DBE=∠C,
∴∠A=90°,∴∠C=30°,故选:D.
练习1.如图,两个三角形为全等三角形,则∠α的度数是( )
A.72°
B.60°
C.58°
D.50°
【答案】A
【解析】解:根据三角形内角和可得∠1=180°﹣50°﹣58°=72°,
因为两个全等三角形,所以∠α=∠1=72°,故选A.
小结
全等的另一个典型性质是对应角相等,在全等形存在的题目中进行角度计算时,一定要注意对这一性质的应用.
全等性质中常见模型的识别
在利用全等三角形的性质进行相关的边、角计算时,除了直接利用性质外,还需要对一些常见的几何结构能够准确识别,从而逐步建立几何感知能力.如:
平移型:
旋转型
翻折型
对调性型
共角型
共边型——其本质也是翻折型
一线三等角之三垂直模型
例1.如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求角F的度数与DH的长;
(2)求证:AB∥DE.
【答案】解:(1)∵∠A=85°,∠B=60°,∴∠ACB=180°﹣∠A﹣∠B=35°,
∵△ABC≌△DEF,AB=8,∴∠F=∠ACB=35°,DE=AB=8,
∵EH=2,∴DH=8﹣2=6;
(2)证明:∵△ABC≌△DEF,∴∠DEF=∠B,∴AB∥DE.
【解析】(1)根据三角形内角和定理求出∠ACB,根据全等三角形的性质得出AB=DE,∠F=∠ACB,即可得出答案;(2)根据全等三角形的性质得出∠B=∠DEF,根据平行线的判定得出即可.
练习1.如图,△ABC≌△DEF,AC∥DF,则∠C的对应角为( )
A.∠F
B.∠AGE
C.∠AEF
D.∠D
【答案】A
【解析】解:∵AC∥DF,∴∠D=∠BAC;
∵△ABC≌△DEF,∴△ABC与△DEF的对应角相等;
又∠C是△ABC的一个内角,∴∠C的对应角应△DEF的一个内角;
A、∠AGE不是△DEF的一个内角,不符合题意;
B、∠AEF不是△DEF的一个内角,不符合题意;
C、∠D与∠BAC是对应角,不符合题意;
故选A.
小结
注意平移型全等形的识别,平移的距离可以有多种情况,两个图形可以没有公共的部分,这也是平移型的一种典型情况,在授课过程中注意帮助学生建立这种模型意识.
例2.已知:如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:∵△ABC≌△AEF,∴AC=AF,故①正确;
∠EAF=∠BAC,∴∠FAC=∠EAB≠∠FAB,故②错误;
EF=BC,故③正确;
∠EAB=∠FAC,故④正确;
综上所述,结论正确的是①③④共3个.故选C.
练习1.如图,△ABC≌△DBE,∠DBC=150°,∠ABD=40°,则∠ABE的度数是( )
A.70°
B.65°
C.60°
D.55°
【答案】A
【解析】解:∵∠DBC=150°,∠ABD=40°,∴∠ABC=110°,
∵△ABC≌△DBE,∴∠DBE=∠ABC=110°,∴∠ABE=∠DBE﹣∠ABD=70°,故选:A.
小结
注意旋转型全等形的识别,旋转的角度也可以有很多种,两个图形可以没有公共的部分,这也是旋转的一种典型情况,在授课过程中注意帮助学生建立这种模型意识.
例3.如图,已知△ABC≌△DCB,AB=10,∠A=60°,∠ABC=80°,那么下列结论中错误的是( )
A.∠D=60°
B.∠DBC=40°
C.AC=DB
D.BE=10
【答案】D
【解析】解:∵∠A=60°,∠ABC=80°,∴∠ACB=40°,
∵△ABC≌△DCB,∴∠D=∠A=60°,∠DBC=∠ACB=40°,AC=BD,
故A,B,C正确,故选D.
练习1.如图,点E,F在线段BC上,△ABF与△DEC全等,其中点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DEC等于( )
A.∠B
B.∠A
C.∠EMF
D.∠AFB
【答案】D
【解析】解:∵△ABF与△DEC全等,点A与点D,点B与点C是对应顶点,
∴△ABF≌△DCE,∴∠DEC=∠AFB,故选:D.
小结
注意翻折型全等形的识别,翻折的本质是轴对称,其中轴对称的知识会在下一章中学到,其中对称轴的位置决定了翻折前后形成的两个图形的位置关系,建议老师在讲解旋转、翻折、平移这三个模型时,要以动态的思想来分析、帮助学生理解不同的形式产生的原因,在授课过程中注意帮助学生建立这种模型意识.
例4.如图,△ABD≌△CDB,下面四个结论中不正确的是( )
A.△ABD和△CDB的面积相等
B.△ABD和△CDB的周长相等
C.∠A+∠ABD=∠C+∠CBD
D.AD∥BC,且AD=BC
【答案】C
【解析】解:∵△ABD≌△CDB,
∴∠ADB=∠CBD,AD=BC,△ABD和△CDB的面积相等,△ABD和△CDB的周长相等,
∴AD∥BC,则选项A,B,D一定正确.
由△ABD≌△CDB不一定能得到∠ABD=∠CBD,
因而∠A+∠ABD=∠C+∠CBD不一定成立.故选C.
练习1.如图,△ABC≌△BAD,若AB=6、AC=4、BC=5,则△BAD的周长为 .
【答案】15
【解析】解:∵△ABC≌△BAD,∴AD=CB=5,BD=AC=4,
∵AB=6,∴△BAD的周长为:5+4+6=15,故答案为:15.
小结
对调型的全等也有不同的位置、不同的情况,其中有一条边完全重合的情况构成的是平行四边形(在人教版初二下学期的课本中会学到),对于这种类型的全等,一定要注意区分其对应点和对应边分别是什么.
例5.如图:若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
A.2
B.3
C.5
D.2.5
【答案】B
【解析】解:∵△ABE≌△ACF,AB=5,∴AC=AB=5,
∵AE=2,∴EC=AC﹣AE=5﹣2=3,故选B.
练习1.如图,△ABE≌△ACF.若AB=5,AE=2,BE=4,则CF的长度是( )
A.2
B.5
C.4
D.3
【答案】C
【解析】解:∵△ABE≌△ACF,∴CF=BE=4,故选:C.
练习2.已知如图,△OAD≌△OBC,且∠O=70°,∠C=25°,则∠OAD=( )
A.95°
B.85°
C.75°
D.65°
【答案】B
【解析】解:∵△OAD≌△OBC,∴∠D=∠C=25°,
∵∠O=70°,∴∠OAD=180°﹣25°﹣70°=85°,故选:B.
小结
共角模型其本质也是翻折的一种,由于它有一个公共角,其情况比较特殊,所以单独拿出来分析,此种模型在下一节的全等判定中出现的频率很高,其中蕴藏着两组全等三角形,两者之间的转化很经典.
例6.如图,△ABC≌△DCB,若AC=7,BE=5,则DE的长为( )
A.2
B.3
C.4
D.5
【答案】A
【解析】解:∵△ABC≌△DCB,∴BD=AC=7,∵BE=5,∴DE=BD﹣BE=2,故选A.
练习1.如图,已知△ABC≌△BAD,A和B,C和D分别是对应顶点,且∠C=60°,∠ABD=35°,则∠BAD的度数是( )
A.60°
B.35°
C.85°
D.不能确定
【答案】C
【解析】解:∵△ABC≌△BAD,∠C=60°,∴∠D=∠C=60°,
∵∠ABD=35°,∴∠BAD=180°﹣∠D﹣∠ABD=180°﹣60°﹣35°=85°,故选C.
小结
共边型全等其本质也是翻折型,是翻折的一个特殊情况.
例7.如图,E为线段AB上一点,AC⊥AB,DB⊥AB,△ACE≌△BED.
(1)试猜想线段CE与DE的位置关系,并证明你的结论;
(2)求证:AB=AC+BD.
【答案】(1)CE⊥DE,
证明:∵AC⊥AB,DB⊥AB,
∴∠A=∠B=90°,∴∠C+∠CEA=90°,
∵△ACE≌△BED,∴∠C=∠DEB,
∴∠CEA+∠DEB=90°,
∴∠CED=180°﹣90°=90°,∴CE⊥DE;
证明:∵△ACE≌△BED,
∴AC=BE,BD=AE,
∴AB=AE+BE=AC+BD.
【解析】(1)求出∠A=∠B=90°,推出∠C+∠CEA=90°,根据全等得出∠C=∠DEB,推出∠CEA+∠DEB=90°即可;(2)根据全等三角形的性质得出AC=BE,BD=AE,即可得出答案.
练习1.如图,已知Rt△ABC≌Rt△CDE,∠B=∠D=90°,且B,C,D三点共线.试说明∠ACE=90°.
【答案】证明:∵Rt△ABC≌Rt△CDE,∴∠BCA=∠CED,
∵△DCE是直角三角形,∴∠CED+∠ECD=90°,
∴∠BCA+∠ECD=90°,∴∠ACE=180°-90°=90°.
【解析】根据Rt△ABC≌Rt△CDE可得∠BCA=∠CED,再根据直角三角形两锐角互余可得∠CED+∠ECD=90°,进而得到∠BCA+∠ECD=90°,再根据角之间的关系可得∠ACE=90°.
小结
三垂直模型其本质也是一种旋转,由于其旋转中心不容易确定,所以将此类情况单独拿出来分析,而三垂直的更一般的情况是一线三等角,它是初三相似中非常重要的一个模型.
当堂总结
本次课重点讲解三角形全等的性质及其相关计算,其中需要学生特别关注的就是一些常见的全等的模型,这也为下一节讲解三角形全等的判定作铺垫,在学习全等三角形章节一定要着重关注常见的全等模型,这对计算和证明都有很好的帮助.
课后作业
1、如图,△ADE≌△BDE,若△ADC的周长为12,AC的长为5,则CB的长为( )
A.8
B.7
C.6
D.5
【答案】B
【解析】解:∵△ADE≌△BDE,∴DA=DB,
△ADC的周长=AC+CD+AD=AC+CD+BD=AC+BC=12,又AC=5,∴BC=7,故选:B.
2、若△ABC≌△DEF,且△ABC的周长为20,AB=5,BC=8,则DF长为( )
A.5
B.8
C.7
D.5或8
【答案】C
【解析】解:∵△ABC的周长为20,AB=5,BC=8,∴AC=20﹣5﹣8=7,
∵△ABC≌△DEF,∴DF=AC=7,故选:C.
3、如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( )
A.AB=AC
B.∠BAE=∠CAD
C.BE=DC
D.AD=DE
【答案】D
【解析】解:∵△ABE≌△ACD,∠1=∠2,∠B=∠C,
∴AB=AC,∠BAE=∠CAD,BE=DC,AD=AE,故A、B、C正确;
AD的对应边是AE而非DE,所以D错误.故选D.
4、如图,△ABD≌△ACE,点B和点C是对应顶点,AB=8,AD=6,BD=7,则CE的长是( )
A.1
B.2
C.4
D.7
【答案】D
【解析】解:∵△ABD≌△ACE,∴BD=CE=7.故选:D.
5、如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=42°,AB=9,AD=6,G为AB延长线上一点.
(1)求∠EBG的度数.
(2)求CE的长.
【答案】解:(1)∵△ABE≌△ACD,∴∠EBA=∠C=42°,∴∠EBG=180°﹣42°=138°;
(2)∵△ABE≌△ACD,∴AC=AB=9,AE=AD=6,∴CE=AC﹣AE=9﹣6=3.
6、如图所示,已知△ABC≌△DCB,∠A=32°,∠BCD=115°,求∠BOC.
【答案】解:∵△ABC≌△DCB,∴∠DBC=∠ACB,∠A=∠D,
△ABC中,∠A=32°,∴∠D=32°,∴∠DBC=∠ACB=180°﹣∠D﹣∠BCD=33°,
∴∠OBC=∠OCB=33°,∴∠BOC=180°﹣33°﹣33°=114°.
【解析】根据三角形内角和定理可求∠DBC=33°,根据全等三角形的性质可证∠DBC=∠ACB,即可求∠BOC.
7、如图,E为线段BC上一点,AB⊥BC,△ABE≌△ECD,判断AE与DE的关系,并证明你的结论.
【答案】解:AE⊥DE.
∵AB⊥BC,∴∠B=90°.
∵△ABE≌△ECD,∴∠A=∠DEC,∠AEB=∠EDC,∠B=∠C=90°.
∵∠A+∠AEB=90°,∠DEC+∠D=90°,∴∠AEB+∠DEC=90°,∴∠AED=90°,即AE⊥DE.
第4页
