沪科版(2012)初中数学九年级上册 23.1.2 锐角的三角函数 课件(共24张PPT)
文档属性
| 名称 | 沪科版(2012)初中数学九年级上册 23.1.2 锐角的三角函数 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 934.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 10:35:44 | ||
图片预览




文档简介
(共24张PPT)
23.1 锐角的三角函数(2)
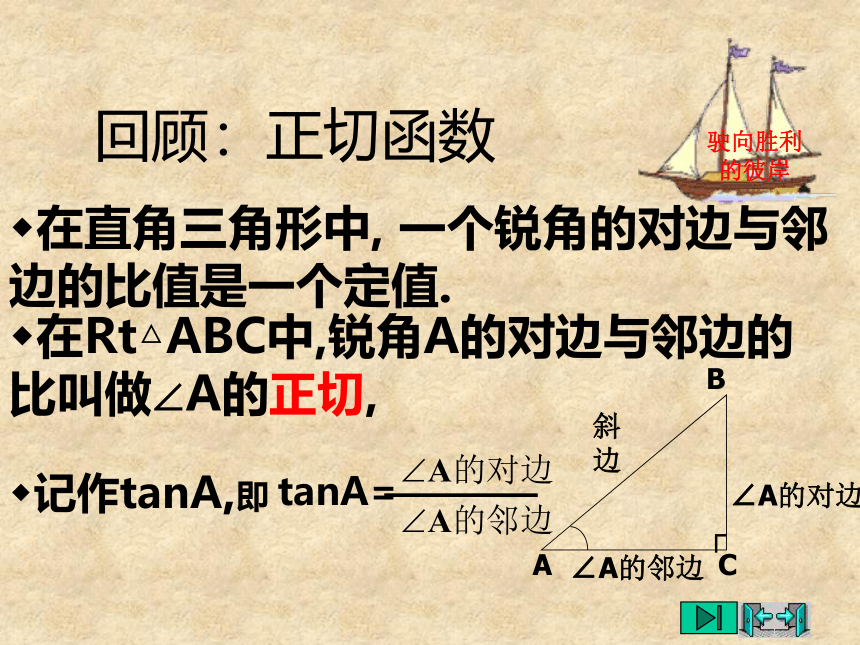
在直角三角形中,
一个锐角的对边与邻边的比值是一个定值.
回顾:正切函数
驶向胜利的彼岸
在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,
记作tanA,即
tanA=
A
B
C
∠A的对边
∠A的邻边
┌
斜边
在Rt△ABC中,对于锐角A的每一个确定的值,其对边与斜边的比值是不是唯一确定的
呢?邻边与斜边的比值?
想一想
本领大不大
悟心来当家
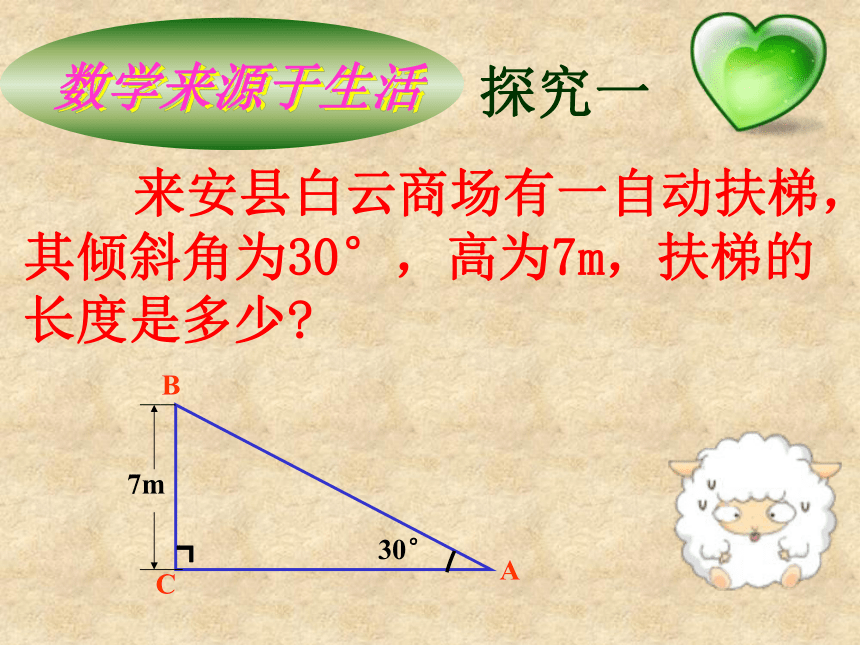
来安县白云商场有一自动扶梯,其倾斜角为30°,高为7m,扶梯的长度是多少?
B
A
C
┓
30°
7m
数学来源于生活
探究一
解:∵在直角三角形中,
由于∠A=30
°,
所以
可得AB=2BC=7×2=14m
所以,扶梯的长度是14m.
已知等腰直角三角形ABC,∠C=90
°,计算∠A的对边与斜边的比
,你能得出什么结论?
A
B
C
┓
探究二
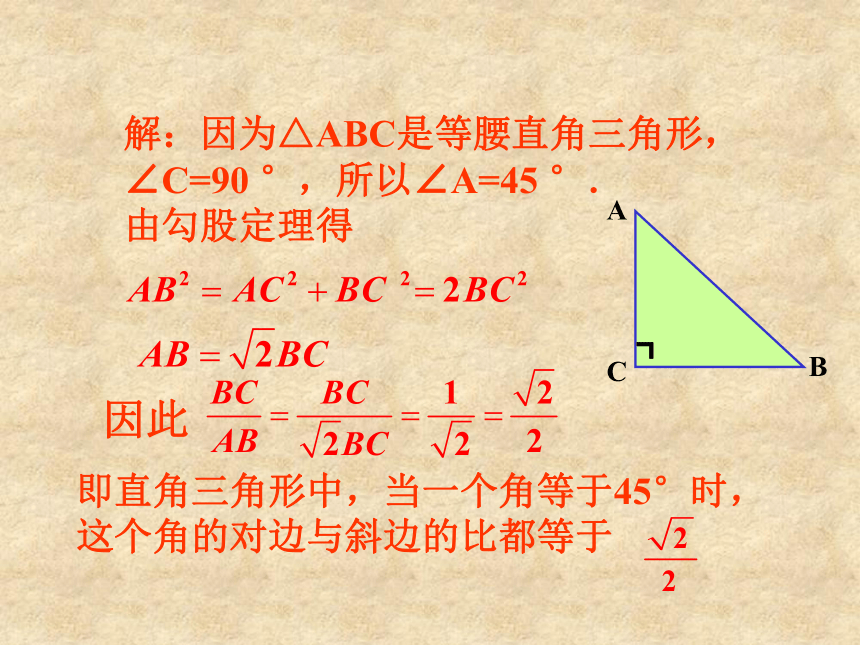
解:因为△ABC是等腰直角三角形,
∠C=90
°,所以∠A=45
°.
由勾股定理得
A
B
C
┓
即直角三角形中,当一个角等于45°时,这个角的对边与斜边的比都等于
因此
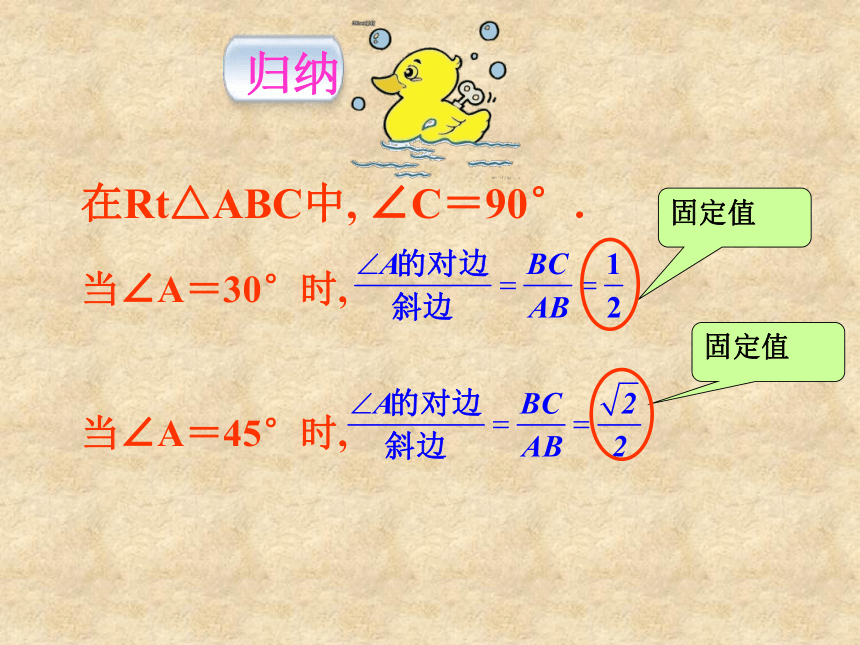
在Rt△ABC中,
∠C=90°.
当∠A=30°时,
当∠A=45°时,
固定值
固定值
归纳
=__________=__________.
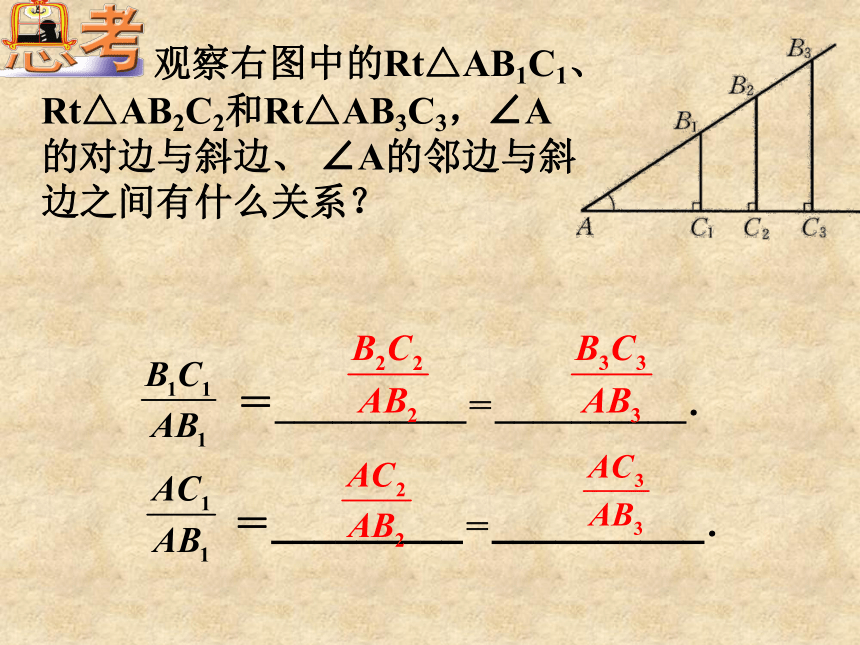
观察右图中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,∠A的对边与斜边、
∠A的邻边与斜边之间有什么关系?
=_________=__________.
在Rt△ABC中,在直角三角形中,当锐角A的度数一定时,无论三角形的大小如何,∠A的对边边与斜边的比、
∠A的邻边与斜边的比、
∠A的对边与邻边的比都是一个固定值.
归纳
A
B
C
∠A的对边
∠A的邻边
┌
斜边
在Rt△ABC中,
∠C=90
°,我们把锐角A的对边与斜边的比叫做∠
A的正弦记作sinA,即
知识要点一
正弦
A
B
C
a
(
C
b
┓
在Rt△ABC中,
∠C=90
°,我们把锐角A的邻边与斜边的比叫做∠
A的余弦记作cosA,即
知识要点二
余弦
A
B
C
a
(
C
b
a
┓
锐角三角函数
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数
知识要点三
[三角函数的表示方法]
1、sinA、cosA、tanA都是整体符号,对于
用三个大写字母表示的角,不能省略角的
符号,如sin∠ADB等;
2、用数字表示的角,也不能省略角的符号,
如sin∠1等;
3、用希腊字母表示的角,可以省略角的符
号,如sinα等.
3.sinA、cosA、tanA
是在直角三角形中定义的,∠A是锐角.
4.锐角A的三角函数值的取值范围
.
正切
tanA>0
正弦
0<
sinA<1
余弦
0<
cosA<1
锐角三角函数定义的几个特点
1.sinA、
cosA、tanA
是一个比值(数值).
2.sinA、
cosA、
tanA
的大小只与∠A的大小有关,而与直角三角形的边长无关.
问题展示:
例1:在Rt⊿ABC中,∠C=Rt∠,AB=13,BC=5,求锐角∠A、
∠B的各三角函数值
A
B
C
13
5
12
┓
书本第116页练习第1题.
小试牛刀
求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值。
例2.如图,
∠C=90°CD⊥AB.
sinB可以由哪两条线段之比?
若AC=5,CD=3,求sinB的值.
┌
A
C
B
D
解:
∵∠B=∠ACD
∴sinB=sin∠ACD
在Rt△ACD中,AD=
sin
∠ACD=
∴sinB=
=4
开动脑筋,点石成金!
书本第116页练习第2题.
相信自己,我能行
八仙过海,尽显才能
驶向胜利的彼岸
通过本节课学习,你有何收获?
1、直角三角形中锐角三角函数的定义。
2、方法:(1)先用勾股定理,再根据定义求;(2)角相等,则其三角函数值相等,利用转化的思想求三角函数值.
3、归纳、整理、类比及转化的数学思想。
课堂小结
回味无穷
.
课堂作业
1(必做):
书本116页练习第3、4
、5题
2(选做):在Rt△ABC,∠C=90°,∠A,∠B
,∠C的对边分别是a,b,c.
求证:sin2A+cos2A=1.
家庭作业:基础训练82页练习二
结束寄语
一个人只要坚持不懈地追求,他就能达到目的.
下课了!
祝同学们天天向上
谢谢大家
感谢各位老师莅临指导
再见
23.1 锐角的三角函数(2)
在直角三角形中,
一个锐角的对边与邻边的比值是一个定值.
回顾:正切函数
驶向胜利的彼岸
在Rt△ABC中,锐角A的对边与邻边的比叫做∠A的正切,
记作tanA,即
tanA=
A
B
C
∠A的对边
∠A的邻边
┌
斜边
在Rt△ABC中,对于锐角A的每一个确定的值,其对边与斜边的比值是不是唯一确定的
呢?邻边与斜边的比值?
想一想
本领大不大
悟心来当家
来安县白云商场有一自动扶梯,其倾斜角为30°,高为7m,扶梯的长度是多少?
B
A
C
┓
30°
7m
数学来源于生活
探究一
解:∵在直角三角形中,
由于∠A=30
°,
所以
可得AB=2BC=7×2=14m
所以,扶梯的长度是14m.
已知等腰直角三角形ABC,∠C=90
°,计算∠A的对边与斜边的比
,你能得出什么结论?
A
B
C
┓
探究二
解:因为△ABC是等腰直角三角形,
∠C=90
°,所以∠A=45
°.
由勾股定理得
A
B
C
┓
即直角三角形中,当一个角等于45°时,这个角的对边与斜边的比都等于
因此
在Rt△ABC中,
∠C=90°.
当∠A=30°时,
当∠A=45°时,
固定值
固定值
归纳
=__________=__________.
观察右图中的Rt△AB1C1、Rt△AB2C2和Rt△AB3C3,∠A的对边与斜边、
∠A的邻边与斜边之间有什么关系?
=_________=__________.
在Rt△ABC中,在直角三角形中,当锐角A的度数一定时,无论三角形的大小如何,∠A的对边边与斜边的比、
∠A的邻边与斜边的比、
∠A的对边与邻边的比都是一个固定值.
归纳
A
B
C
∠A的对边
∠A的邻边
┌
斜边
在Rt△ABC中,
∠C=90
°,我们把锐角A的对边与斜边的比叫做∠
A的正弦记作sinA,即
知识要点一
正弦
A
B
C
a
(
C
b
┓
在Rt△ABC中,
∠C=90
°,我们把锐角A的邻边与斜边的比叫做∠
A的余弦记作cosA,即
知识要点二
余弦
A
B
C
a
(
C
b
a
┓
锐角三角函数
锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数
知识要点三
[三角函数的表示方法]
1、sinA、cosA、tanA都是整体符号,对于
用三个大写字母表示的角,不能省略角的
符号,如sin∠ADB等;
2、用数字表示的角,也不能省略角的符号,
如sin∠1等;
3、用希腊字母表示的角,可以省略角的符
号,如sinα等.
3.sinA、cosA、tanA
是在直角三角形中定义的,∠A是锐角.
4.锐角A的三角函数值的取值范围
.
正切
tanA>0
正弦
0<
sinA<1
余弦
0<
cosA<1
锐角三角函数定义的几个特点
1.sinA、
cosA、tanA
是一个比值(数值).
2.sinA、
cosA、
tanA
的大小只与∠A的大小有关,而与直角三角形的边长无关.
问题展示:
例1:在Rt⊿ABC中,∠C=Rt∠,AB=13,BC=5,求锐角∠A、
∠B的各三角函数值
A
B
C
13
5
12
┓
书本第116页练习第1题.
小试牛刀
求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值。
例2.如图,
∠C=90°CD⊥AB.
sinB可以由哪两条线段之比?
若AC=5,CD=3,求sinB的值.
┌
A
C
B
D
解:
∵∠B=∠ACD
∴sinB=sin∠ACD
在Rt△ACD中,AD=
sin
∠ACD=
∴sinB=
=4
开动脑筋,点石成金!
书本第116页练习第2题.
相信自己,我能行
八仙过海,尽显才能
驶向胜利的彼岸
通过本节课学习,你有何收获?
1、直角三角形中锐角三角函数的定义。
2、方法:(1)先用勾股定理,再根据定义求;(2)角相等,则其三角函数值相等,利用转化的思想求三角函数值.
3、归纳、整理、类比及转化的数学思想。
课堂小结
回味无穷
.
课堂作业
1(必做):
书本116页练习第3、4
、5题
2(选做):在Rt△ABC,∠C=90°,∠A,∠B
,∠C的对边分别是a,b,c.
求证:sin2A+cos2A=1.
家庭作业:基础训练82页练习二
结束寄语
一个人只要坚持不懈地追求,他就能达到目的.
下课了!
祝同学们天天向上
谢谢大家
感谢各位老师莅临指导
再见
