冀教版初中数学七年级上册 1.8 有理数的乘法 课件(共14张PPT)
文档属性
| 名称 | 冀教版初中数学七年级上册 1.8 有理数的乘法 课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 904.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 10:43:19 | ||
图片预览




文档简介
(共14张PPT)
复习导入
2、本课规定:把“当前时刻”记为0分钟,2分钟以后记为+2分钟,那么3分钟前应记为
。
O
2
4
6
8
3、一蜗牛在数轴上爬行,现在正处在原点O处。若它以每分2cm的速度向右爬,3分钟后它什么位置?
-4
-2
1、(-2)
+3=
(-3)+2=
(-2)+(-3)=
加法
负数意义
导入
(+2)×(+3)=
+6
+1
-1
-5
-3分钟
有理数的乘法
一.列乘法算式
O
2
4
6
8
-6
-4
-2
右
(-2)
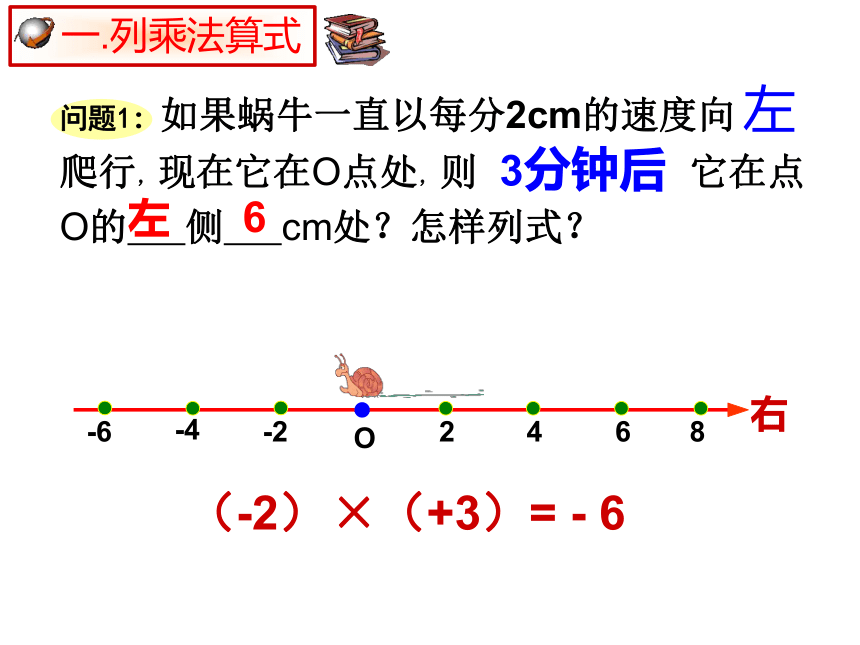
问题1:如果蜗牛一直以每分2cm的速度向
爬行,现在它在O点处,则
它在点O的
侧
cm处?怎样列式?
左
3分钟后
左
6
×(+3)=
-
6
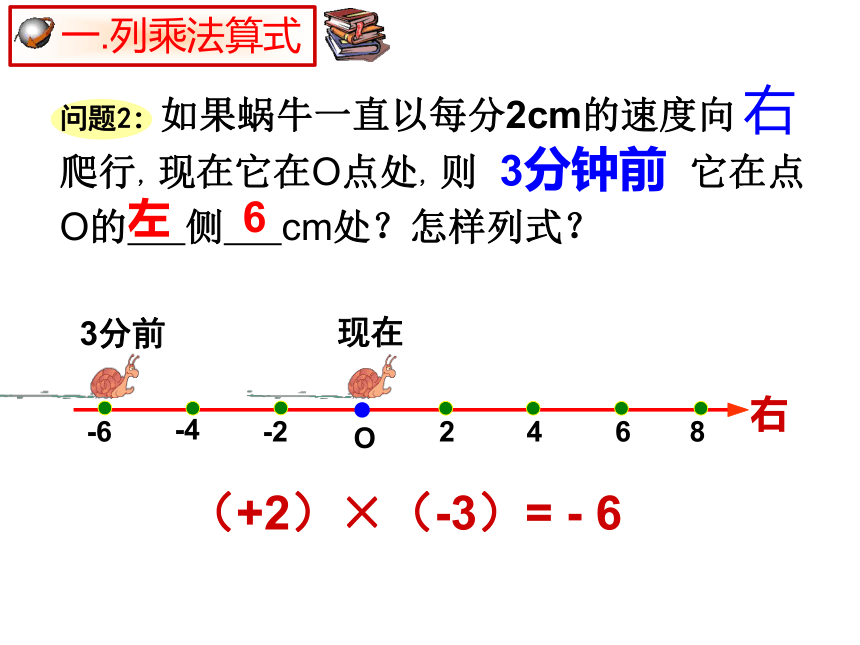
问题2:如果蜗牛一直以每分2cm的速度向
爬行,现在它在O点处,则
它在点O的
侧
cm处?怎样列式?
右
3分钟前
O
2
4
6
8
-6
-4
-2
右
(+2)×(-3)=
-
6
现在
3分前
一.列乘法算式
左
6
一.列乘法算式
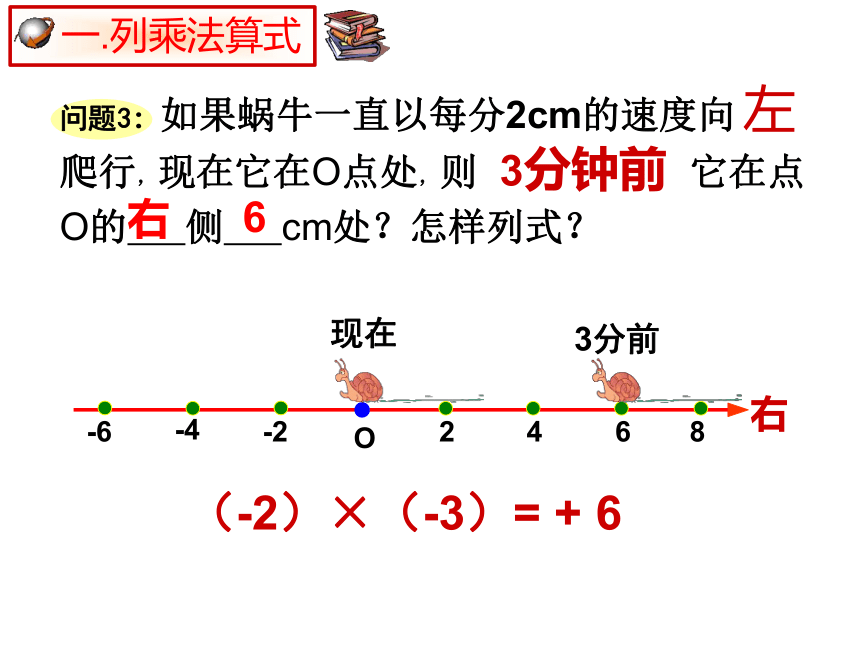
问题3:如果蜗牛一直以每分2cm的速度向
爬行,现在它在O点处,则
它在点O的
侧
cm处?怎样列式?
左
3分钟前
O
2
4
6
8
-6
-4
-2
右
(-2)×(-3)=
+
6
现在
3分前
右
6
一.列乘法算式
问题3:如果蜗牛一直以每分2cm的速度向
爬行,现在它在O点处,则
它在点O的
侧
cm处?怎样列式?
左
3分钟前
O
2
4
6
8
-6
-4
-2
右
(-2)×(-3)=
+
6
0
×(-3)=
?
(-2)×
0
=
?
0
二.由算式到法则
(+2
)×(+3
)=
+
6
(-2
)×(+3
)=
-
6
(+2
)×(-3
)=
-
6
(-2
)×(-3
)
=
+
6
(-2
)×
0
=
0
0
×(-3
)
=
0
二.由算式到法则
(+2
)×(+3
)=
+
6
(-2
)×(+3
)=
-
6
(+2
)×(-3
)=
-
6
(-2
)×(-3
)
=
+
6
(-2
)×
0
=
0
0
×(-3
)
=
0
同号两数相乘,
并把两数绝对值相乘。
异号两数相乘,
任何数与0相乘,积
积为正。
积为负。
为0。
有理数乘法法则。
三.
法则应用
-30.5
-0.2
=
+(30.5
×0.2
)
乘以
=
+
6.1
例1:
(
)×
(
)
运算符号与性质符号间要用(
)隔开.
做乘时,可先确定积的符号,再算绝对值.
收获:
练习:
列式计算
1
1
三.
法则应用
1
1
倒数:有理数中,乘积是1的两个数互为倒数
+1
-1
-
3
13
-
10
7
无
1
a
3
13
…
+1
原数
-1
-0.7
它的倒数
-4
1
3
4
1
3
0
a
(a≠0)
四.
对比深化
(-2
)×(-3
)
=
(-2
)
+
(-3
)
=
(-2
)×(+3
)=
(-2
)
+
(+3
)=
(+2
)
+
(-3
)=
(-2
)×
0
=
(-2
)
+
0
=
口算:
+6
-5
-6
+1
-1
0
-2
二.由算式到法则
(+2
)×(+3
)=
+
6
(-2
)×(+3
)=
-
6
(+2
)×(-3
)=
-
6
(-2
)×(-3
)
=
+
6
(-2
)×
0
=
0
0
×(-3
)
=
0
要使两数之积为
,这两个数得满
足哪些条件?
+2
-2
课
堂
小
结
这节课,
我做了…
我发现了…
我学会了…
四.
对比深化
(-2
)×(-3
)
=
(-2
)
+
(-3
)
=
(-2
)×(+3
)=
(-2
)
+
(+3
)=
(+2
)
+
(-3
)=
(-2
)×
0
=
(-2
)
+
0
=
口算:
+6
-5
-6
+1
-1
0
-2
编题:
编:积为-5的式子,
和为-5的式子。
复习导入
2、本课规定:把“当前时刻”记为0分钟,2分钟以后记为+2分钟,那么3分钟前应记为
。
O
2
4
6
8
3、一蜗牛在数轴上爬行,现在正处在原点O处。若它以每分2cm的速度向右爬,3分钟后它什么位置?
-4
-2
1、(-2)
+3=
(-3)+2=
(-2)+(-3)=
加法
负数意义
导入
(+2)×(+3)=
+6
+1
-1
-5
-3分钟
有理数的乘法
一.列乘法算式
O
2
4
6
8
-6
-4
-2
右
(-2)
问题1:如果蜗牛一直以每分2cm的速度向
爬行,现在它在O点处,则
它在点O的
侧
cm处?怎样列式?
左
3分钟后
左
6
×(+3)=
-
6
问题2:如果蜗牛一直以每分2cm的速度向
爬行,现在它在O点处,则
它在点O的
侧
cm处?怎样列式?
右
3分钟前
O
2
4
6
8
-6
-4
-2
右
(+2)×(-3)=
-
6
现在
3分前
一.列乘法算式
左
6
一.列乘法算式
问题3:如果蜗牛一直以每分2cm的速度向
爬行,现在它在O点处,则
它在点O的
侧
cm处?怎样列式?
左
3分钟前
O
2
4
6
8
-6
-4
-2
右
(-2)×(-3)=
+
6
现在
3分前
右
6
一.列乘法算式
问题3:如果蜗牛一直以每分2cm的速度向
爬行,现在它在O点处,则
它在点O的
侧
cm处?怎样列式?
左
3分钟前
O
2
4
6
8
-6
-4
-2
右
(-2)×(-3)=
+
6
0
×(-3)=
?
(-2)×
0
=
?
0
二.由算式到法则
(+2
)×(+3
)=
+
6
(-2
)×(+3
)=
-
6
(+2
)×(-3
)=
-
6
(-2
)×(-3
)
=
+
6
(-2
)×
0
=
0
0
×(-3
)
=
0
二.由算式到法则
(+2
)×(+3
)=
+
6
(-2
)×(+3
)=
-
6
(+2
)×(-3
)=
-
6
(-2
)×(-3
)
=
+
6
(-2
)×
0
=
0
0
×(-3
)
=
0
同号两数相乘,
并把两数绝对值相乘。
异号两数相乘,
任何数与0相乘,积
积为正。
积为负。
为0。
有理数乘法法则。
三.
法则应用
-30.5
-0.2
=
+(30.5
×0.2
)
乘以
=
+
6.1
例1:
(
)×
(
)
运算符号与性质符号间要用(
)隔开.
做乘时,可先确定积的符号,再算绝对值.
收获:
练习:
列式计算
1
1
三.
法则应用
1
1
倒数:有理数中,乘积是1的两个数互为倒数
+1
-1
-
3
13
-
10
7
无
1
a
3
13
…
+1
原数
-1
-0.7
它的倒数
-4
1
3
4
1
3
0
a
(a≠0)
四.
对比深化
(-2
)×(-3
)
=
(-2
)
+
(-3
)
=
(-2
)×(+3
)=
(-2
)
+
(+3
)=
(+2
)
+
(-3
)=
(-2
)×
0
=
(-2
)
+
0
=
口算:
+6
-5
-6
+1
-1
0
-2
二.由算式到法则
(+2
)×(+3
)=
+
6
(-2
)×(+3
)=
-
6
(+2
)×(-3
)=
-
6
(-2
)×(-3
)
=
+
6
(-2
)×
0
=
0
0
×(-3
)
=
0
要使两数之积为
,这两个数得满
足哪些条件?
+2
-2
课
堂
小
结
这节课,
我做了…
我发现了…
我学会了…
四.
对比深化
(-2
)×(-3
)
=
(-2
)
+
(-3
)
=
(-2
)×(+3
)=
(-2
)
+
(+3
)=
(+2
)
+
(-3
)=
(-2
)×
0
=
(-2
)
+
0
=
口算:
+6
-5
-6
+1
-1
0
-2
编题:
编:积为-5的式子,
和为-5的式子。
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
