人教版八年级数学上册15.2分式的运算讲义(教师版)
文档属性
| 名称 | 人教版八年级数学上册15.2分式的运算讲义(教师版) | 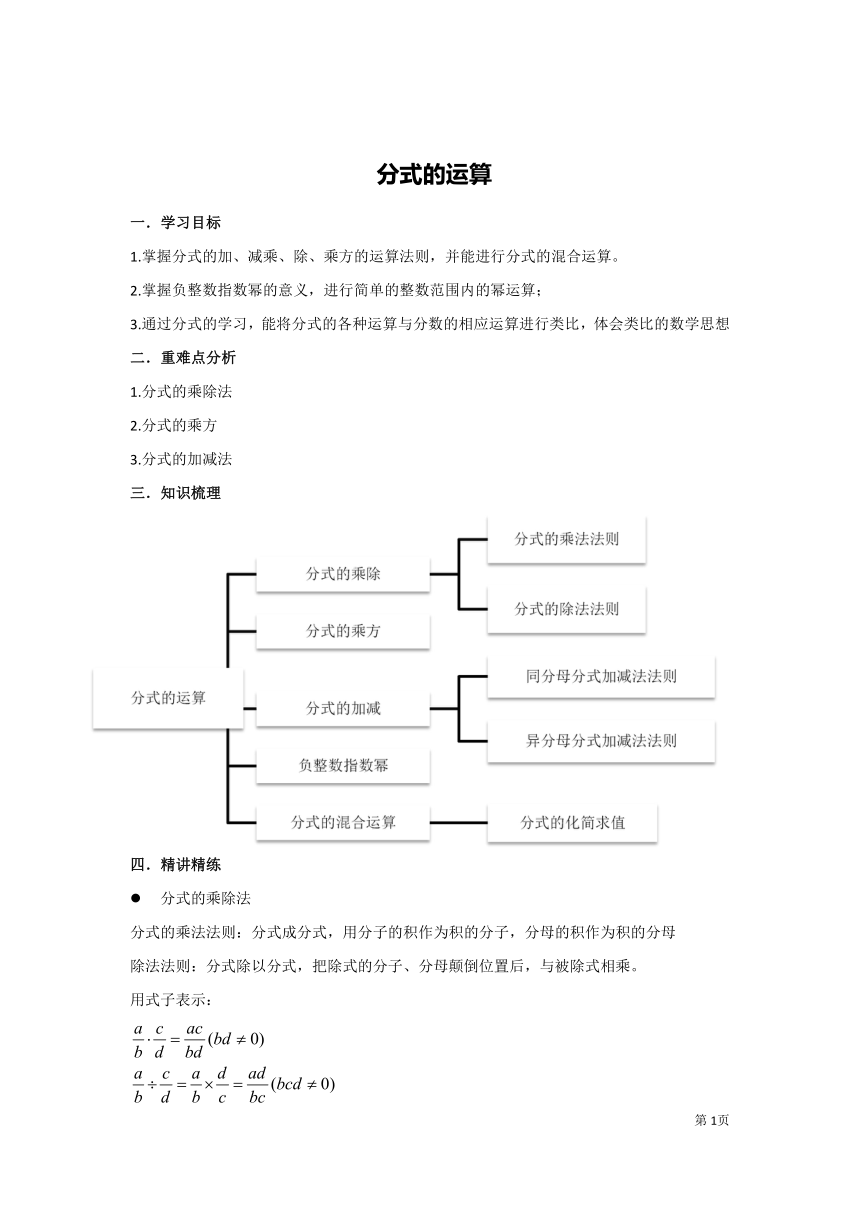 | |
| 格式 | zip | ||
| 文件大小 | 270.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 08:54:14 | ||
图片预览





文档简介
一.学习目标
掌握分式的加、减乘、除、乘方的运算法则,并能进行分式的混合运算。
掌握负整数指数幂的意义,进行简单的整数范围内的幂运算;
通过分式的学习,能将分式的各种运算与分数的相应运算进行类比,体会类比的数学思想
二.重难点分析
分式的乘除法
分式的乘方
分式的加减法
三.知识梳理
四.精讲精练
分式的乘除法
分式的乘法法则:分式成分式,用分子的积作为积的分子,分母的积作为积的分母
除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。
用式子表示:
注意事项:
分式与分式相乘,若分子、分母都是单项式,可先将分子、分母分别相乘,然后约去公因式,化为最简分式;若分子、分母是多项式,先把分子、分母分解因式,看能否约分然后在相乘。
当整式和分式相乘时,要把整式(看作是分母为1的式子)与分式的分子相乘作为积的分子,分式的分母作为积的分母。当整式是多项式时,同样要先分解因式,看能否约分,然后再相乘。
分式的除法运算可以转化为分式的乘法运算,若除式(或被除式)是整式时,可以看作是分母是1的式子,然后依照分式除法法则计算。
分式的乘除的运算结果要通过约分化为最简分式(分式的分子、分母没有公因式)或整式的形式。
分式的乘除混合运算,如果没有其他附加条件(如括号等),则按照由左向右的顺序进行计算。
例1.计算的结果是( )
A.
B.
C.
D.
【答案】D
练习1.计算:
【解析】原式==
小结
分式乘分式,若分子和分母是单项式,可先将分子、分母分别相乘,然后约去公因式。
例2.化简
【解析】解:原式=
练习1.?= .
【解析】解:原式=?=,
练习2.化简的结果为 .
【解析】解:原式=?=x+1,
小结
分式乘分式,若分子和分母是多项式,先把分子、分母分解因式,看能否约分,然后再相乘。
例3.
计算(-a)2·
的结果为(
?
?)
A.b
B.-b
C.ab
D.
【答案】A
练习.?5(a+1)2等于( )
A.a2+2a+1
B.5a2+10
a+5
C.5a2﹣1
D.5a2﹣5
【答案】D
【解析】解:原式=×5(a+1)2=5(a+1)(a﹣1)=5a2﹣5
小结
当整式与分式相乘时,要把整式看作分母为1的分式,然后再运算分式乘法的法则进行运算。
例4.化简:(1)
=
(2)÷=
.
【答案】(1)-a;(2)
【解析】解:(1)原式=
=-a.
(2)÷=?=,
练习1.计算(1)÷
(2)÷.
(3)(xy﹣x2)÷÷.
【解析】解:(1)原式=÷=×=﹣
(2)原式=×=﹣=﹣
(3)原式=﹣x(x﹣y)?=﹣y.
小结
分式的乘除法,关键是约分,约分的关键是找公因式.在寻找公因式时经常要把分子分母分解因式,互为相反数的因式是比较易忽视的问题.在解题中一定要引起注意.
分式的乘方
分式的乘方法则:分式乘方要把分子、分母分别乘方。用式子表示:
例1.
计算:()2的结果是( )
A.
B.
C.
D.
【解析】解:原式=,故选C
练习1.
()3()4÷()3.
【解析】解:原式=﹣??(﹣)=.
练习2.
()5?(﹣)4÷(﹣mn4)
【解析】解:原式=?÷(﹣mn4)=mn3?(﹣)=﹣.
小结
乘方运算,先定符号,再把分子分母分别乘方即可。
分式的加减法
分式的加减法法则:
同分母分式相加减,分母不变,把分子相加减,
异分母分式相加减,先通分,变为同分母的分式再加减,
例1.计算
的结果是(
?
?)
A.2
B.2a+2
C.1
D.
【答案】A
练习1.计算﹣的结果是( )
A.
B.
C.
D.
【答案】C
小结
同分母的分式的加法,分母不变,分子相加减。
例2.计算:= .
【解析】解:原式===x+y.故答案为x+y.
练习1.计算:
+
= .
【解答】解:原式=
+
=
,
练习2.计算:
【解析】原式==﹣x﹣y;
练习3.化简:﹣.
【解析】解:原式=+==a﹣1.
练习4.化简:.
【解析】解:原式=﹣==x.
小结
观察题目,分母互为相反数的,通过变号通分。
例3.化简:﹣,结果正确的是( )
A.1
B.
C.
D.x2+y2
【解析】解:原式==.故选B
练习1.化简﹣的结果是( )
A.
B.
C.
D.
【解析】解:原式=﹣=。故选(A)
练习2.化简:﹣= .
【解析】解:﹣=﹣=x+1﹣x﹣1=0.
小结
分母为没有公因式的,最简公分母就是分母相乘。
例4.化简﹣的结果是( )
A.﹣x2+2x
B.﹣x2+6x
C.﹣
D.
【答案】C
【解析】解:原式=﹣==﹣
练习1.计算
的结果是____
【答案】
【解析】解:原式
.
小结
先求通分,通分时,注意分式的性质。
例5.化简﹣.
【解答】解:原式=﹣===﹣.
练习.化简:+﹣.
【解析】解:原式=+﹣,=+﹣,
=+﹣,=﹣,
=﹣,=.
小结
本题考查了分式的加减法,要牢记异分母分式加减法法则:把分母不相同的几个分式化成分母相同的分式,叫做通分,经过通分,异分母分式的加减就转化为同分母分式的加减.
例6.化简:.
【解答】解:=++2=++2
=++==
练习.计算:+﹣x.
【解析】解:原式===1.
小结
当出现分式加整式(数)时,先把整式(数)看作分母为1的式子,再通分,然后进行加减。
例7..
【解析】解:原式=﹣=.
练习.a﹣1﹣.
【解答】
a﹣1﹣=﹣=﹣.
小结
注意符号;
出现整式时,先先写为分母为1
的式子,再通分,然后进行分式的加减。
分式的混合运算
分式的混合运算,关键是弄清运算顺序,与分数的加减乘除及乘方的混合运算一样,先乘方,再算乘除,最后算加减。有括号要先算括号里面的,在运算过程中药注意正确地运用运算法则,灵活地运用运算律,使运算尽量简便。
例1.化简:(a+)(1﹣)的结果等于( )
A.a﹣2
B.a+2
C.
D.
【答案】B
【解答】解:?=?=a+2.
练习.
化简:(﹣)(﹣),
【解析】解:原式=[+]?[﹣]
=?(﹣)=?=x﹣2,
小结
分式运算和分数运算一样,结果必须化为最简,能约分的要约分。
例2.化简:(+)÷.
【解答】解:(+)÷====.
练习1.
化简(﹣)的结果是( )
A.x
B.
C.
D.
【答案】A
【解析】解:原式=?=?=x,
练习2.
化简,
【答案】见解析
【解析】解:原式=
=
=
=
练习3.
化简:(﹣)÷.
【解析】解:(﹣)÷
==
=
=
=
.
小结
有括号的混合运算,可以先算括号里的,在进行除法运算,也可以先去括号。
例3.计算(a+2+)÷(a﹣).
【解析】解:(a+2+)÷(a﹣)===.
练习.化简:?(1+).
【解答】解:原式=?=.
小结
分式的混合运算,熟练掌握运算法则是解本题的关键.
例4.化简:.
【答案】﹣2
【解析】解:原式=(﹣)?=﹣==﹣2
练习1.计算.
【答案】见解析
解:原式
练习2.计算:÷(a﹣1)+.
【解答】解:原式=×+
=+=+=.
小结
(1)若分式中含有整式,应视其分母为1进行约分或通分;
(2)合理搭配,分组通分,先约分再通分;
例5.
已知a=b+2018,求代数式?÷的值.
【解析】解:原式=××(a﹣b)(a+b)=2(a﹣b)
∵a=b+2018,∴原式=2×2018=4036
练习1.
已知[(x2+y2)-(x-y)2+2y(x-y)]÷4y的值为1,求
的值.
【答案】
【解析】解:∵[(x2+y2)-(x-y)2+2y(x-y)]÷4y
=(x2+y2-x2+2xy-y2+2xy-2y2)÷4y
=(4xy-2y2)÷4y
=x-y
=1,即2x-y=2,
∴原式=
=
=
=.
小结
正确的使用相应的运算法则和运算顺序;正确的使用运算律,尽量简化运算过程;结果必须化为最简。
负整数指数幂
一般地,当是正整数时,(),即()是的倒数
例1.
(-π)0+2-2=____.
【答案】.
【解析】解:原式=(-π)0+2-2,=1+
,=.
练习1.
计算:0.125×(﹣)﹣3﹣(π﹣3.14)0=
.
【答案】﹣2
【解析】解:原式=[0.5×(﹣2)]3﹣1=﹣1﹣1=﹣2,
练习2.
计算:﹣4﹣1﹣(﹣2)0+3÷.
【解析】解:原式=﹣﹣1+3÷9=﹣﹣1+=﹣.
小结
先确定符号,再熟练运用。
例2.某种细菌的直径是0.00000078米,将数据0.00000078用科学记数法表示为( )
A.7.8×10﹣7
B.7.8×10﹣8
C.0.78×10﹣7
D.78×10﹣8
【答案】A
练习1.人体中红细胞的直径约为0.0000077m,将数0.0000077用科学记数法表示为(
?
?)
A.77×10-5
B.0.77×10-7
C.7.7×10-6
D.7.7×10-7
【答案】C
小结
本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
五.当堂总结
分式基本运算
分式的乘法:
分式的除法:
乘方:(为正整数)
整数指数幂运算性质:
⑴(、为整数)
⑵(、为整数)
⑶(为整数)
⑷(,、为整数)
负整指数幂:一般地,当是正整数时,(),即()是的倒数
分式的加减法法则:
同分母分式相加减,分母不变,把分子相加减,
异分母分式相加减,先通分,变为同分母的分式再加减,
分式的混合运算的运算顺序:先算乘方,再算乘除,后算加减,如有括号,括号内先算.
结果以最简形式存在.
六.课后作业
1.
【答案】
【解析】原式=
=
=
2.先化简,再求值:(
)÷
,其中x=
-2.
【答案】
【解析】解:原式=
=
当x=
-2时,原式=
=
3.先化简:
÷
?(x?
),然后x在-1,0,1,2四个数中选一个你认为合适的数代入求值.
【答案】见解析
【解析】解:原式=
?
?
,
=
?
,
=x+1.
∵在-1,0,1,2四个数中,使原式有意义的值只有2,
∴当x=2时,原式=2+1=3.
4.计算
÷(a2﹣4)?.
【解析】解:原式==.
5.计算:.
【解析】解:原式==,
=,=.
6.
已知a2+3a+1=0,试求的值
【解析】解:因为a2+3a+1=0,将等式两边同时除以a(a≠0)
所以,两边同时平方,得=9,
所以,两边再次平方,得
所以+2=49.∴=47.
7.
先化简,再求值:(﹣)÷,其中x=2y(xy≠0).
【解析】解:(﹣)÷
====,
当x=2y时,原式=.
8.
先化简,再求值:(﹣)(﹣),其中x=4.
【解析】解:原式=[+]?[﹣]
=?(﹣)=?=x﹣2,
当x=4时,原式=4﹣2=2.
9.
先化简,再求值:(+)÷,且x为满足﹣3<x<2的整数.
【解析】解:(+)÷
=[+]×x=(+)×x=2x﹣3
∵x为满足﹣3<x<2的整数,
∴x=﹣2,﹣1,0,1,∵x要使原分式有意义,
∴x≠﹣2,0,1,∴x=﹣1,
当x=﹣1时,原式=2×(﹣1)﹣3=﹣5
10.
化简:(﹣)÷.
【答案】见解析
【解析】解:(﹣)÷
==
===.
11.
计算:(﹣2016)0﹣2﹣2﹣(﹣)﹣3﹣(﹣3)2.
【解析】解:原式=1﹣+8﹣9=﹣.
第6页
掌握分式的加、减乘、除、乘方的运算法则,并能进行分式的混合运算。
掌握负整数指数幂的意义,进行简单的整数范围内的幂运算;
通过分式的学习,能将分式的各种运算与分数的相应运算进行类比,体会类比的数学思想
二.重难点分析
分式的乘除法
分式的乘方
分式的加减法
三.知识梳理
四.精讲精练
分式的乘除法
分式的乘法法则:分式成分式,用分子的积作为积的分子,分母的积作为积的分母
除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。
用式子表示:
注意事项:
分式与分式相乘,若分子、分母都是单项式,可先将分子、分母分别相乘,然后约去公因式,化为最简分式;若分子、分母是多项式,先把分子、分母分解因式,看能否约分然后在相乘。
当整式和分式相乘时,要把整式(看作是分母为1的式子)与分式的分子相乘作为积的分子,分式的分母作为积的分母。当整式是多项式时,同样要先分解因式,看能否约分,然后再相乘。
分式的除法运算可以转化为分式的乘法运算,若除式(或被除式)是整式时,可以看作是分母是1的式子,然后依照分式除法法则计算。
分式的乘除的运算结果要通过约分化为最简分式(分式的分子、分母没有公因式)或整式的形式。
分式的乘除混合运算,如果没有其他附加条件(如括号等),则按照由左向右的顺序进行计算。
例1.计算的结果是( )
A.
B.
C.
D.
【答案】D
练习1.计算:
【解析】原式==
小结
分式乘分式,若分子和分母是单项式,可先将分子、分母分别相乘,然后约去公因式。
例2.化简
【解析】解:原式=
练习1.?= .
【解析】解:原式=?=,
练习2.化简的结果为 .
【解析】解:原式=?=x+1,
小结
分式乘分式,若分子和分母是多项式,先把分子、分母分解因式,看能否约分,然后再相乘。
例3.
计算(-a)2·
的结果为(
?
?)
A.b
B.-b
C.ab
D.
【答案】A
练习.?5(a+1)2等于( )
A.a2+2a+1
B.5a2+10
a+5
C.5a2﹣1
D.5a2﹣5
【答案】D
【解析】解:原式=×5(a+1)2=5(a+1)(a﹣1)=5a2﹣5
小结
当整式与分式相乘时,要把整式看作分母为1的分式,然后再运算分式乘法的法则进行运算。
例4.化简:(1)
=
(2)÷=
.
【答案】(1)-a;(2)
【解析】解:(1)原式=
=-a.
(2)÷=?=,
练习1.计算(1)÷
(2)÷.
(3)(xy﹣x2)÷÷.
【解析】解:(1)原式=÷=×=﹣
(2)原式=×=﹣=﹣
(3)原式=﹣x(x﹣y)?=﹣y.
小结
分式的乘除法,关键是约分,约分的关键是找公因式.在寻找公因式时经常要把分子分母分解因式,互为相反数的因式是比较易忽视的问题.在解题中一定要引起注意.
分式的乘方
分式的乘方法则:分式乘方要把分子、分母分别乘方。用式子表示:
例1.
计算:()2的结果是( )
A.
B.
C.
D.
【解析】解:原式=,故选C
练习1.
()3()4÷()3.
【解析】解:原式=﹣??(﹣)=.
练习2.
()5?(﹣)4÷(﹣mn4)
【解析】解:原式=?÷(﹣mn4)=mn3?(﹣)=﹣.
小结
乘方运算,先定符号,再把分子分母分别乘方即可。
分式的加减法
分式的加减法法则:
同分母分式相加减,分母不变,把分子相加减,
异分母分式相加减,先通分,变为同分母的分式再加减,
例1.计算
的结果是(
?
?)
A.2
B.2a+2
C.1
D.
【答案】A
练习1.计算﹣的结果是( )
A.
B.
C.
D.
【答案】C
小结
同分母的分式的加法,分母不变,分子相加减。
例2.计算:= .
【解析】解:原式===x+y.故答案为x+y.
练习1.计算:
+
= .
【解答】解:原式=
+
=
,
练习2.计算:
【解析】原式==﹣x﹣y;
练习3.化简:﹣.
【解析】解:原式=+==a﹣1.
练习4.化简:.
【解析】解:原式=﹣==x.
小结
观察题目,分母互为相反数的,通过变号通分。
例3.化简:﹣,结果正确的是( )
A.1
B.
C.
D.x2+y2
【解析】解:原式==.故选B
练习1.化简﹣的结果是( )
A.
B.
C.
D.
【解析】解:原式=﹣=。故选(A)
练习2.化简:﹣= .
【解析】解:﹣=﹣=x+1﹣x﹣1=0.
小结
分母为没有公因式的,最简公分母就是分母相乘。
例4.化简﹣的结果是( )
A.﹣x2+2x
B.﹣x2+6x
C.﹣
D.
【答案】C
【解析】解:原式=﹣==﹣
练习1.计算
的结果是____
【答案】
【解析】解:原式
.
小结
先求通分,通分时,注意分式的性质。
例5.化简﹣.
【解答】解:原式=﹣===﹣.
练习.化简:+﹣.
【解析】解:原式=+﹣,=+﹣,
=+﹣,=﹣,
=﹣,=.
小结
本题考查了分式的加减法,要牢记异分母分式加减法法则:把分母不相同的几个分式化成分母相同的分式,叫做通分,经过通分,异分母分式的加减就转化为同分母分式的加减.
例6.化简:.
【解答】解:=++2=++2
=++==
练习.计算:+﹣x.
【解析】解:原式===1.
小结
当出现分式加整式(数)时,先把整式(数)看作分母为1的式子,再通分,然后进行加减。
例7..
【解析】解:原式=﹣=.
练习.a﹣1﹣.
【解答】
a﹣1﹣=﹣=﹣.
小结
注意符号;
出现整式时,先先写为分母为1
的式子,再通分,然后进行分式的加减。
分式的混合运算
分式的混合运算,关键是弄清运算顺序,与分数的加减乘除及乘方的混合运算一样,先乘方,再算乘除,最后算加减。有括号要先算括号里面的,在运算过程中药注意正确地运用运算法则,灵活地运用运算律,使运算尽量简便。
例1.化简:(a+)(1﹣)的结果等于( )
A.a﹣2
B.a+2
C.
D.
【答案】B
【解答】解:?=?=a+2.
练习.
化简:(﹣)(﹣),
【解析】解:原式=[+]?[﹣]
=?(﹣)=?=x﹣2,
小结
分式运算和分数运算一样,结果必须化为最简,能约分的要约分。
例2.化简:(+)÷.
【解答】解:(+)÷====.
练习1.
化简(﹣)的结果是( )
A.x
B.
C.
D.
【答案】A
【解析】解:原式=?=?=x,
练习2.
化简,
【答案】见解析
【解析】解:原式=
=
=
=
练习3.
化简:(﹣)÷.
【解析】解:(﹣)÷
==
=
=
=
.
小结
有括号的混合运算,可以先算括号里的,在进行除法运算,也可以先去括号。
例3.计算(a+2+)÷(a﹣).
【解析】解:(a+2+)÷(a﹣)===.
练习.化简:?(1+).
【解答】解:原式=?=.
小结
分式的混合运算,熟练掌握运算法则是解本题的关键.
例4.化简:.
【答案】﹣2
【解析】解:原式=(﹣)?=﹣==﹣2
练习1.计算.
【答案】见解析
解:原式
练习2.计算:÷(a﹣1)+.
【解答】解:原式=×+
=+=+=.
小结
(1)若分式中含有整式,应视其分母为1进行约分或通分;
(2)合理搭配,分组通分,先约分再通分;
例5.
已知a=b+2018,求代数式?÷的值.
【解析】解:原式=××(a﹣b)(a+b)=2(a﹣b)
∵a=b+2018,∴原式=2×2018=4036
练习1.
已知[(x2+y2)-(x-y)2+2y(x-y)]÷4y的值为1,求
的值.
【答案】
【解析】解:∵[(x2+y2)-(x-y)2+2y(x-y)]÷4y
=(x2+y2-x2+2xy-y2+2xy-2y2)÷4y
=(4xy-2y2)÷4y
=x-y
=1,即2x-y=2,
∴原式=
=
=
=.
小结
正确的使用相应的运算法则和运算顺序;正确的使用运算律,尽量简化运算过程;结果必须化为最简。
负整数指数幂
一般地,当是正整数时,(),即()是的倒数
例1.
(-π)0+2-2=____.
【答案】.
【解析】解:原式=(-π)0+2-2,=1+
,=.
练习1.
计算:0.125×(﹣)﹣3﹣(π﹣3.14)0=
.
【答案】﹣2
【解析】解:原式=[0.5×(﹣2)]3﹣1=﹣1﹣1=﹣2,
练习2.
计算:﹣4﹣1﹣(﹣2)0+3÷.
【解析】解:原式=﹣﹣1+3÷9=﹣﹣1+=﹣.
小结
先确定符号,再熟练运用。
例2.某种细菌的直径是0.00000078米,将数据0.00000078用科学记数法表示为( )
A.7.8×10﹣7
B.7.8×10﹣8
C.0.78×10﹣7
D.78×10﹣8
【答案】A
练习1.人体中红细胞的直径约为0.0000077m,将数0.0000077用科学记数法表示为(
?
?)
A.77×10-5
B.0.77×10-7
C.7.7×10-6
D.7.7×10-7
【答案】C
小结
本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
五.当堂总结
分式基本运算
分式的乘法:
分式的除法:
乘方:(为正整数)
整数指数幂运算性质:
⑴(、为整数)
⑵(、为整数)
⑶(为整数)
⑷(,、为整数)
负整指数幂:一般地,当是正整数时,(),即()是的倒数
分式的加减法法则:
同分母分式相加减,分母不变,把分子相加减,
异分母分式相加减,先通分,变为同分母的分式再加减,
分式的混合运算的运算顺序:先算乘方,再算乘除,后算加减,如有括号,括号内先算.
结果以最简形式存在.
六.课后作业
1.
【答案】
【解析】原式=
=
=
2.先化简,再求值:(
)÷
,其中x=
-2.
【答案】
【解析】解:原式=
=
当x=
-2时,原式=
=
3.先化简:
÷
?(x?
),然后x在-1,0,1,2四个数中选一个你认为合适的数代入求值.
【答案】见解析
【解析】解:原式=
?
?
,
=
?
,
=x+1.
∵在-1,0,1,2四个数中,使原式有意义的值只有2,
∴当x=2时,原式=2+1=3.
4.计算
÷(a2﹣4)?.
【解析】解:原式==.
5.计算:.
【解析】解:原式==,
=,=.
6.
已知a2+3a+1=0,试求的值
【解析】解:因为a2+3a+1=0,将等式两边同时除以a(a≠0)
所以,两边同时平方,得=9,
所以,两边再次平方,得
所以+2=49.∴=47.
7.
先化简,再求值:(﹣)÷,其中x=2y(xy≠0).
【解析】解:(﹣)÷
====,
当x=2y时,原式=.
8.
先化简,再求值:(﹣)(﹣),其中x=4.
【解析】解:原式=[+]?[﹣]
=?(﹣)=?=x﹣2,
当x=4时,原式=4﹣2=2.
9.
先化简,再求值:(+)÷,且x为满足﹣3<x<2的整数.
【解析】解:(+)÷
=[+]×x=(+)×x=2x﹣3
∵x为满足﹣3<x<2的整数,
∴x=﹣2,﹣1,0,1,∵x要使原分式有意义,
∴x≠﹣2,0,1,∴x=﹣1,
当x=﹣1时,原式=2×(﹣1)﹣3=﹣5
10.
化简:(﹣)÷.
【答案】见解析
【解析】解:(﹣)÷
==
===.
11.
计算:(﹣2016)0﹣2﹣2﹣(﹣)﹣3﹣(﹣3)2.
【解析】解:原式=1﹣+8﹣9=﹣.
第6页
