人教版数学七年级 上册3.1.2用等式的性质解方程课件(19张)
文档属性
| 名称 | 人教版数学七年级 上册3.1.2用等式的性质解方程课件(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 598.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 23:06:18 | ||
图片预览





文档简介
(共19张PPT)
回顾旧知
3,4,5,6,7,8是方程
下列式子哪些是方程?哪些是一元一次方程?
4,6,8是一元一次方程
知识
准备
创设情景
(
)
(
)
的解吗?
、你能估算出方程
4
12
3
2
3
4
2
+
-
=
-
+
x
x
x
等式的性质
学习目标
1、掌握等式的性质;
2、会利用等式的性质解方程。
学生阅读课文81页,说明什么?
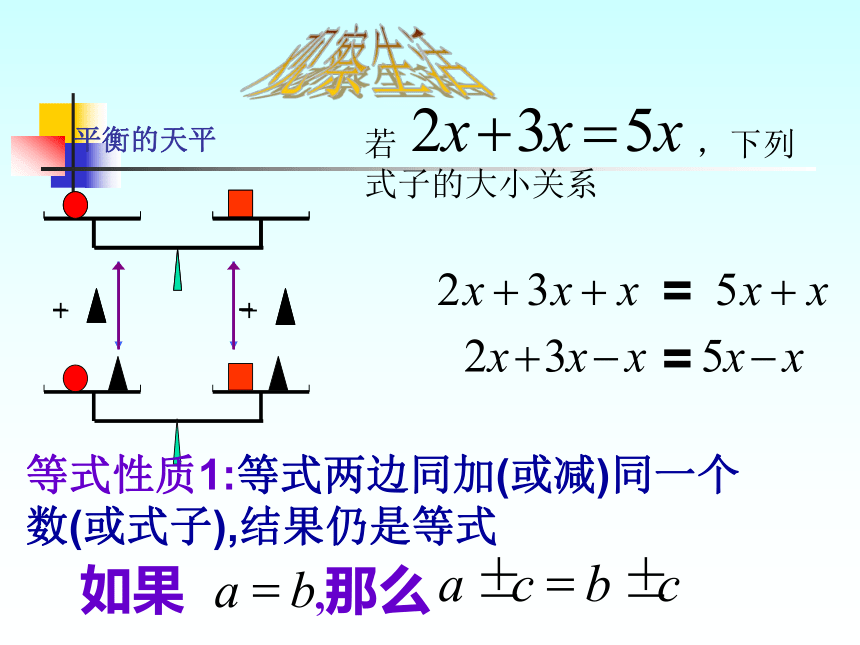
观察生活
平衡的天平
+
+
-
-
若
,下列式子的大小关系
等式性质1:等式两边同加(或减)同一个数(或式子),结果仍是等式
如果 ,那么
c
b
c
a
±
=
±
b
a
=
=
=
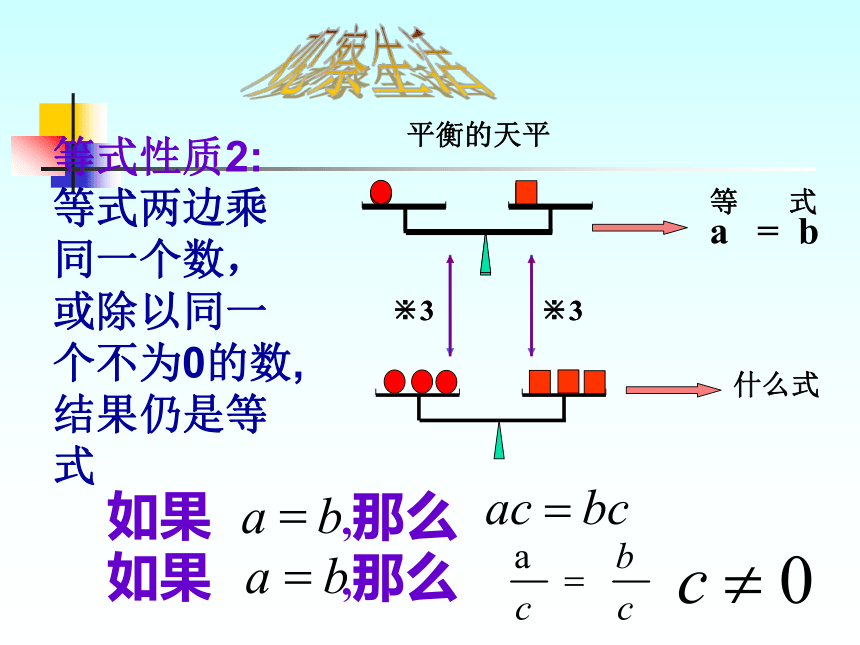
观察生活
平衡的天平
×3
等
式
a
=
b
什么式
×3
÷3
÷3
等式性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍是等式
如果 ,那么
b
a
=
如果 ,那么
b
a
=
等
式
的
性
质
【等式性质2】
【等式性质1】
?
注意
?
1、等式两边都要参加运算,并且是作同一种运算。
2、等式两边加或减,乘或除以的数一定是同一个数或同一个式子。
3、等式两边不能都除以0,即0不能作除数或分母.
如果
,
那么
(
)
如果
,
那么
(
)
如果
,那么
(
)
如果
,那么
(
)
如果
,那么
(
)
如果
,那么
(
)
练一练:判断对错,对的请说出根据等式的哪
一条性质,错的请说出为什么。
√
×
×
×
√
√
练习:1.下列方程变形是否正确?如果正确,说
明变形的根据;如果不正确,说明理由。
(1)由x=y,得x+3=y+3
(2)由a=b,得a-6=b+6
(3)由m=n,得m-2x2=n-2x2
(4)由2x=x-5,得2x+x=-5
(5)由x=y,y=5.3,得x=5.3
(6)由-2=x,得x=-2
依据:等式性质1:等式两边同时加上3.
依据:等式性质1:等式两边同时减去2x2.
左边加x,右边减去x.运算符号不一致
等式的传递性。
等式的对称性。
3、判断下列说法是否成立,并说明理由
( )
( )
( )
(因为x可能等于0)
(等量代换)
(对称性)
.
用等式的性质解方程
解:(1)两边减7得
(2)两边同时除以-5得
(3)两边加5,得
化简得:
两边同乘-3,得
经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的
式:
x
=
a(常数)
即方程左边只一个未知数项、且未知数项的系数是
1,右边只一个常数项.
(6)
(5)
两边同时除以5,得
两边同时减2,得
两边同时乘2,得
两边同除以0.3,得
(4)
8
=
x
两边同时减4,得
2
我应用
根据
。
根据
。
.
(3)、如果4x=-12y,那么x=
,
根据
。
(4)、如果-0.2x=6,那么x=
,
根据
。
(2)、如果x-3=2,那么x-3+3=
,
2x0.5
等式性质2,在等式两边同时乘2
等式性质1,在等式两边同加3
2+3
-3y
等式性质2,在等式两边同时除以4
-30
等式性质2,在等式两边同除-0.2或乘-5
1
、
2、下列变形符合等式性质的是(
)
A、如果2x-3=7,那么2x=7-3
B、如果3x-2=1,那么3x=1-2
C、如果-2x=5,那么x=5+2
3、依据等式性质进行变形,用得不正确的是(
)
D
D
记住了
?
归纳、总结
【等式性质
2】
【等式性质1】
?
注意
?
1、等式两边都要参加运算,并且是作同一种运算。 2、等式两边加或减,乘或除以的数一定是同一个数或同一个式子。
3、等式两边不能都除以0,即0不能作除数或分母.
在学习了等式的性质后,小红发现运用等式的性质可以使复杂的等式变得简洁,这使她异常兴奋,于是她随手写了一个等式:3a+b-2=7a+b-2,并开始运用等式性质对这个等式进行变形,其过程如下:
3a+b=7a+b(等式两边同时加上2)
3a=7a(等式两边同时减去b)
3=7(等式两边同时除以a)
变形到此,小红顿时就傻了:居然得出如此等式!于是小红开始检查自己的变形过程,但怎么也找不出错误来。
聪明的同学,你能让小红的愁眉在恍然大悟中舒展开来吗?
拓展提高
作
业
P83习
题
3.1的第4题.
回顾旧知
3,4,5,6,7,8是方程
下列式子哪些是方程?哪些是一元一次方程?
4,6,8是一元一次方程
知识
准备
创设情景
(
)
(
)
的解吗?
、你能估算出方程
4
12
3
2
3
4
2
+
-
=
-
+
x
x
x
等式的性质
学习目标
1、掌握等式的性质;
2、会利用等式的性质解方程。
学生阅读课文81页,说明什么?
观察生活
平衡的天平
+
+
-
-
若
,下列式子的大小关系
等式性质1:等式两边同加(或减)同一个数(或式子),结果仍是等式
如果 ,那么
c
b
c
a
±
=
±
b
a
=
=
=
观察生活
平衡的天平
×3
等
式
a
=
b
什么式
×3
÷3
÷3
等式性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍是等式
如果 ,那么
b
a
=
如果 ,那么
b
a
=
等
式
的
性
质
【等式性质2】
【等式性质1】
?
注意
?
1、等式两边都要参加运算,并且是作同一种运算。
2、等式两边加或减,乘或除以的数一定是同一个数或同一个式子。
3、等式两边不能都除以0,即0不能作除数或分母.
如果
,
那么
(
)
如果
,
那么
(
)
如果
,那么
(
)
如果
,那么
(
)
如果
,那么
(
)
如果
,那么
(
)
练一练:判断对错,对的请说出根据等式的哪
一条性质,错的请说出为什么。
√
×
×
×
√
√
练习:1.下列方程变形是否正确?如果正确,说
明变形的根据;如果不正确,说明理由。
(1)由x=y,得x+3=y+3
(2)由a=b,得a-6=b+6
(3)由m=n,得m-2x2=n-2x2
(4)由2x=x-5,得2x+x=-5
(5)由x=y,y=5.3,得x=5.3
(6)由-2=x,得x=-2
依据:等式性质1:等式两边同时加上3.
依据:等式性质1:等式两边同时减去2x2.
左边加x,右边减去x.运算符号不一致
等式的传递性。
等式的对称性。
3、判断下列说法是否成立,并说明理由
( )
( )
( )
(因为x可能等于0)
(等量代换)
(对称性)
.
用等式的性质解方程
解:(1)两边减7得
(2)两边同时除以-5得
(3)两边加5,得
化简得:
两边同乘-3,得
经过对原方程的一系列变形(两边同加减、乘除),最终把方程化为最简的
式:
x
=
a(常数)
即方程左边只一个未知数项、且未知数项的系数是
1,右边只一个常数项.
(6)
(5)
两边同时除以5,得
两边同时减2,得
两边同时乘2,得
两边同除以0.3,得
(4)
8
=
x
两边同时减4,得
2
我应用
根据
。
根据
。
.
(3)、如果4x=-12y,那么x=
,
根据
。
(4)、如果-0.2x=6,那么x=
,
根据
。
(2)、如果x-3=2,那么x-3+3=
,
2x0.5
等式性质2,在等式两边同时乘2
等式性质1,在等式两边同加3
2+3
-3y
等式性质2,在等式两边同时除以4
-30
等式性质2,在等式两边同除-0.2或乘-5
1
、
2、下列变形符合等式性质的是(
)
A、如果2x-3=7,那么2x=7-3
B、如果3x-2=1,那么3x=1-2
C、如果-2x=5,那么x=5+2
3、依据等式性质进行变形,用得不正确的是(
)
D
D
记住了
?
归纳、总结
【等式性质
2】
【等式性质1】
?
注意
?
1、等式两边都要参加运算,并且是作同一种运算。 2、等式两边加或减,乘或除以的数一定是同一个数或同一个式子。
3、等式两边不能都除以0,即0不能作除数或分母.
在学习了等式的性质后,小红发现运用等式的性质可以使复杂的等式变得简洁,这使她异常兴奋,于是她随手写了一个等式:3a+b-2=7a+b-2,并开始运用等式性质对这个等式进行变形,其过程如下:
3a+b=7a+b(等式两边同时加上2)
3a=7a(等式两边同时减去b)
3=7(等式两边同时除以a)
变形到此,小红顿时就傻了:居然得出如此等式!于是小红开始检查自己的变形过程,但怎么也找不出错误来。
聪明的同学,你能让小红的愁眉在恍然大悟中舒展开来吗?
拓展提高
作
业
P83习
题
3.1的第4题.
