华师大版九年级数学上册 第24章 解直角三角形 单元检测试题(word版含答案)
文档属性
| 名称 | 华师大版九年级数学上册 第24章 解直角三角形 单元检测试题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 248.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 07:33:55 | ||
图片预览

文档简介
第24章
解直角三角形
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
在中,是直角,,那么的度数是(
)
A.
B.
C.
D.
?
2.
用计算器计算的结果(精确到)是(
)
A.
B.
C.
D.
?
3.
在中,=,如果=,,那么的长是(
)
A.
B.
C.
D.
?
4.
在中,=,若,则的值是(
)
A.
B.
C.
D.
?
5.
如图,某地修建高速公路,要从地向地修一座隧道(、在同一水平面上).为了测量、两地之间的距离,某工程师乘坐热气球从地出发,垂直上升到达处,在处观察地的俯角为,则、两地之间的距离为(
)
A.
B.
C.
D.
?
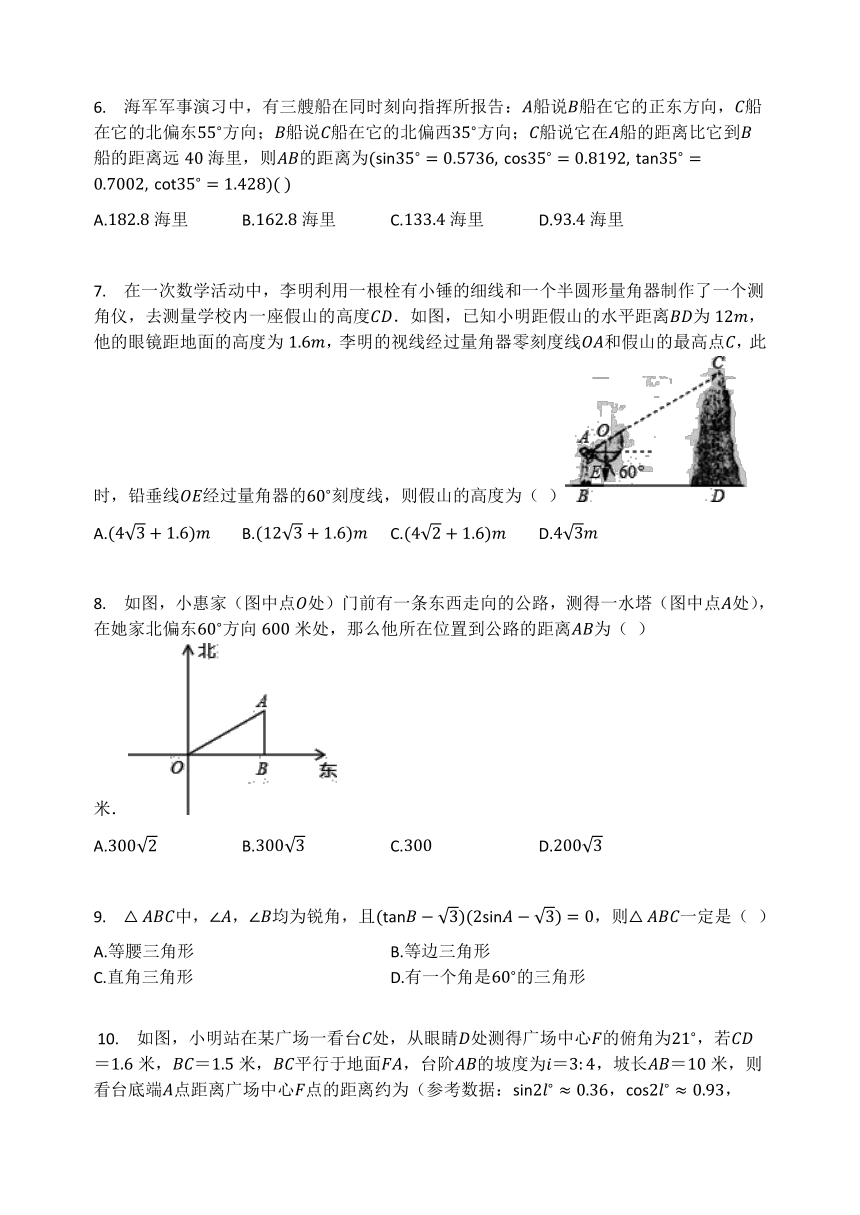
6.
海军军事演习中,有三艘船在同时刻向指挥所报告:船说船在它的正东方向,船在它的北偏东方向;船说船在它的北偏西方向;船说它在船的距离比它到船的距离远海里,则的距离为
A.海里
B.海里
C.海里
D.海里
?
7.
在一次数学活动中,李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度.如图,已知小明距假山的水平距离为,他的眼镜距地面的高度为,李明的视线经过量角器零刻度线和假山的最高点,此时,铅垂线经过量角器的刻度线,则假山的高度为(
)
A.
B.
C.
D.
?
8.
如图,小惠家(图中点处)门前有一条东西走向的公路,测得一水塔(图中点处),在她家北偏东方向米处,那么他所在位置到公路的距离为(
)米.
A.
B.
C.
D.
?
9.
中,,均为锐角,且,则一定是(
)
A.等腰三角形
B.等边三角形
C.直角三角形
D.有一个角是的三角形
?10.
如图,小明站在某广场一看台处,从眼睛处测得广场中心的俯角为,若=米,=米,平行于地面,台阶的坡度为=,坡长=米,则看台底端点距离广场中心点的距离约为(参考数据:,,)(
)
A.米
B.米
C.米
D.米
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
若,则________.
?
12.
在中,,,,则的值是________.
?
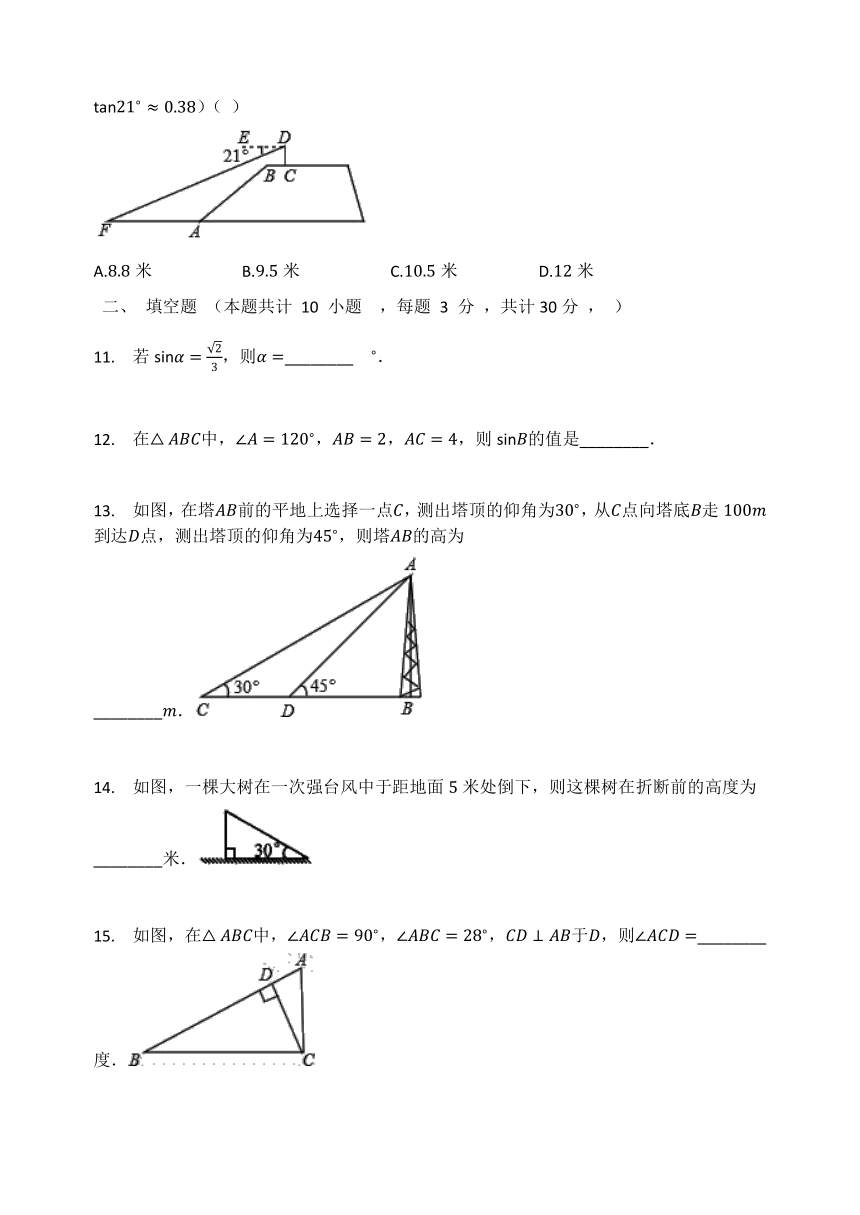
13.
如图,在塔前的平地上选择一点,测出塔顶的仰角为,从点向塔底走到达点,测出塔顶的仰角为,则塔的高为________.
?
14.
如图,一棵大树在一次强台风中于距地面米处倒下,则这棵树在折断前的高度为________米.
?
15.
如图,在中,,,于,则________度.
?
16.
在中,=,=,,则=________.
?
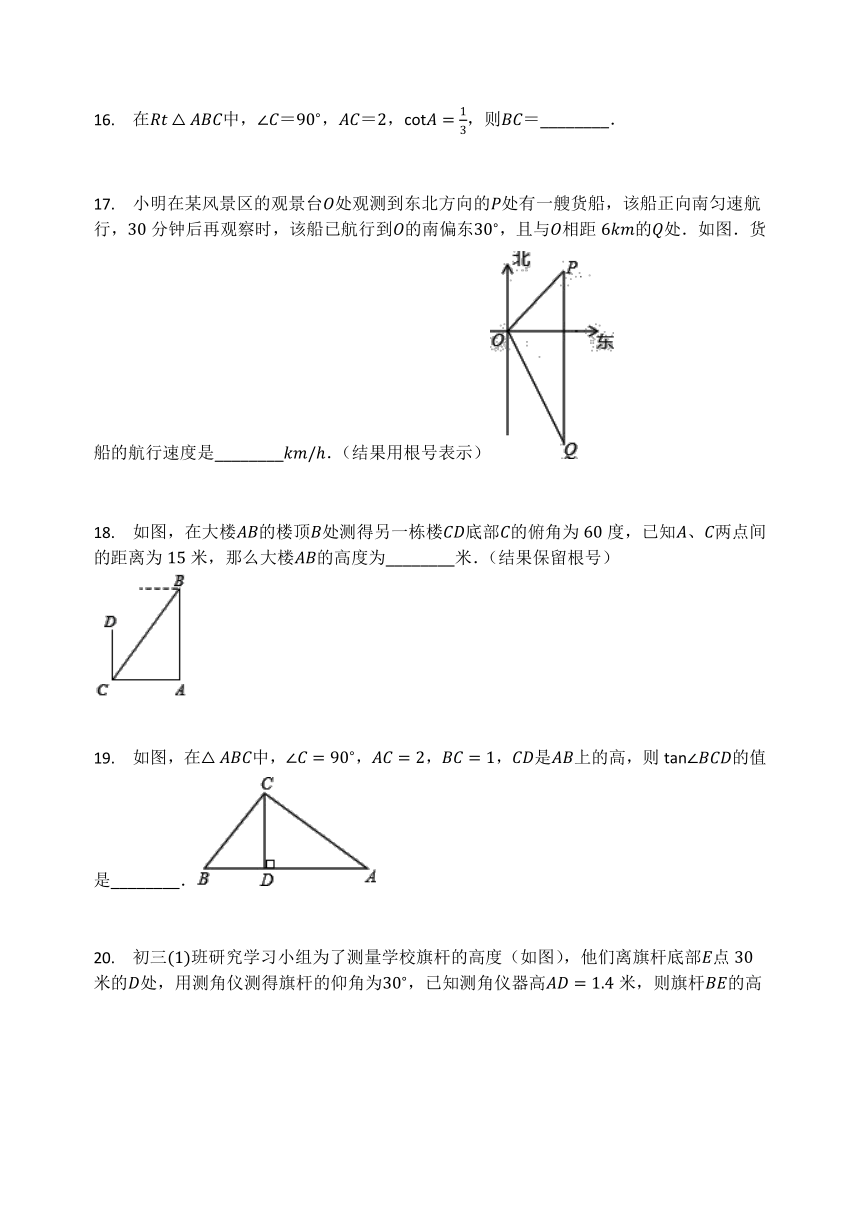
17.
小明在某风景区的观景台处观测到东北方向的处有一艘货船,该船正向南匀速航行,分钟后再观察时,该船已航行到的南偏东,且与相距的处.如图.货船的航行速度是________.(结果用根号表示)
?
18.
如图,在大楼的楼顶处测得另一栋楼底部的俯角为度,已知、两点间的距离为米,那么大楼的高度为________米.(结果保留根号)
?
19.
如图,在中,,,,是上的高,则的值是________.
?
20.
初三班研究学习小组为了测量学校旗杆的高度(如图),他们离旗杆底部点米的处,用测角仪测得旗杆的仰角为,已知测角仪器高米,则旗杆的高为________米(精确到米).
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
计算:
(1)
(2).
?
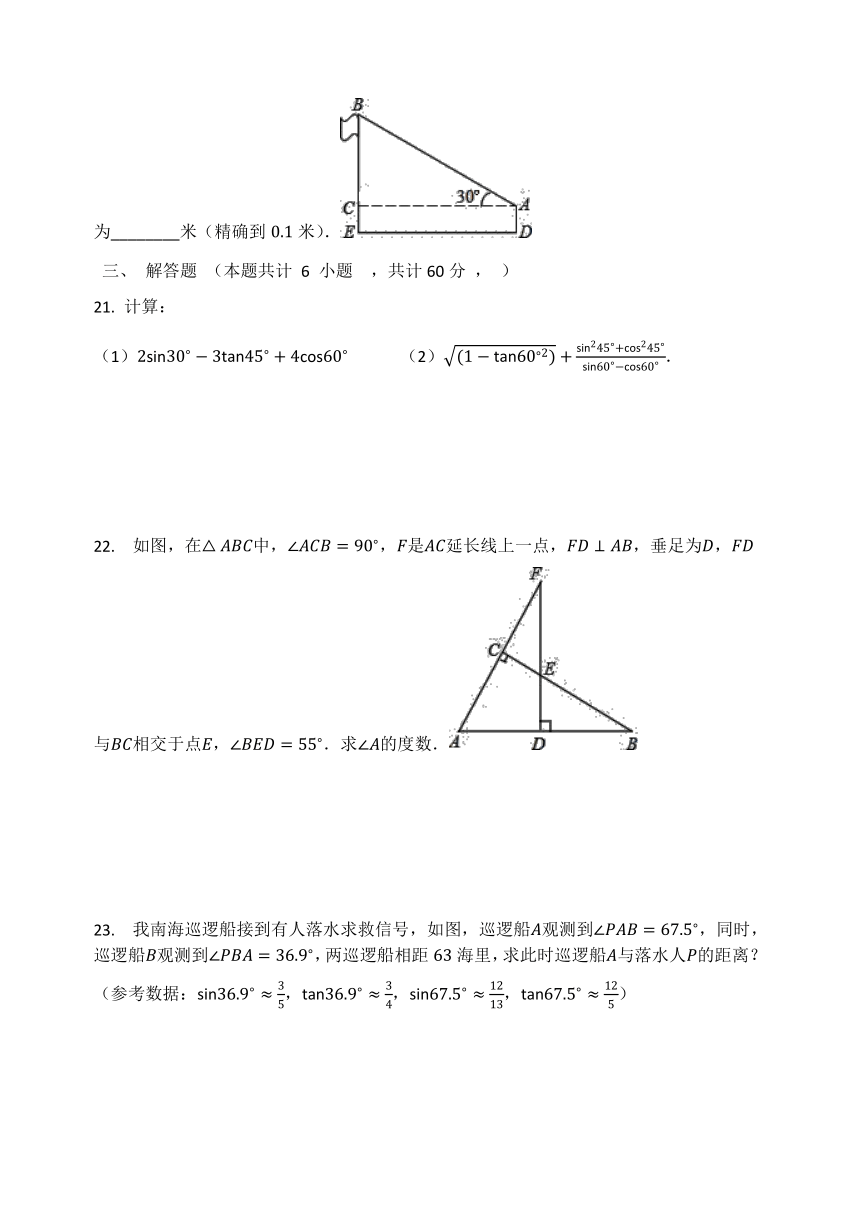
22.
如图,在中,,是延长线上一点,,垂足为,与相交于点,.求的度数.
?
23.
我南海巡逻船接到有人落水求救信号,如图,巡逻船观测到,同时,巡逻船观测到,两巡逻船相距海里,求此时巡逻船与落水人的距离?(参考数据:,,,)
?
24.
如图,在中,,的垂直平分线与,的交点分别为,.
(1)若,,求的长和的值;
(2)若,求的值.(结果保留根号)
?
25.
如图,某学校的教室多媒体投影仪正对投影幕布的中央,其距离米.为了方便课堂教学与使用,现将投影幕布由黑板正中的位置调整到左面的位置处,测得米,,此时投影仪调整到线段上的点处且恰好正对投影幕布的中央.若投影仪与投影幕布的安装距离控制在米到米之间礼堂效果最好,则调整后的投影仪与投影幕布之间的距离是否符合要求?(参考数据:,,,,可用科学计算器,结果精确到)
?
26.
重庆大坪时代天街已成为人们周末休闲娱乐的重要场所,时代天街从一楼到二楼有一自动扶梯(如图),图是侧面示意图.已知自动扶梯的坡度为,,是二楼楼顶,,是上处在自动扶梯顶端正上方的一点,且,在自动扶梯底端处测得点仰角为.
为了吸引顾客,开发商想在处放置一个高的《疯狂动物城》的装饰雕像,并要求雕像最高点与二楼顶层要留出距离好放置灯具,请问这个雕像能放得下吗?如果不能,请说明理由.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【解答】
解:.
故选.
2.
【解答】
解:用计算器解.
故选.
3.
【解答】
∵
,
∴
,
4.
【解答】
∵
=,即=,
∴
,
解得或(舍去),
∴
.
5.
【解答】
根据题意得:=,,=,
在中,.
6.
【解答】
解:,
∴
,即是直角三角形.
,
又∵
∴
解得:(海里)
故选.
7.
【解答】
解:∵
米,李明的眼睛高米,,
∴
,米,,
∴
,
解得(米),
即米.
故选:.
8.
【解答】
解:由已知得,,.
则.
故选.
9.
【解答】
∵
中,,均为锐角,且,
∴
或,
即或.
∴
或.
∴
有一个角是.
10.
【解答】
如图,作交的延长线于,延长交的延长线于.
∵
=,=米,
∴
=(米),=(米),
在中,,
∴
,
∴
(米),
∴
==(米),
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【解答】
解:∵
,
∴
.
故答案为:.
12.
【解答】
解:作于,如图,
∵
,
∴
,
在中,,
∵
,
∴
,
∵
,
∴
,
∴
,
在中,,
∴
.
故答案为.
13.
【解答】
解:在中,
∵
,
∴
.
在中,
∵
,
,
∴
.
设(米),
∵
,
∴
.
∴
,
∴
,
故答案为:
14.
【解答】
解:设树断处到顶部长,
∴
,
∴
.
∴
此树长.
15.
【解答】
解:∵
,
∴
,
∵
在中,,
∴
,
∴
.
故答案为:.
16.
【解答】
中,=,=,,得
===,
17.
【解答】
解:如图,在直角中,,,,
∴
,.
在直角中,,,,
∴
,
∴
,
∴
货船的航行速度是.
故答案为.
18.
【解答】
由题意得,=,=,=,
∴
,
∴
=,
19.
【解答】
解:∵
,,
∴
,
∴
,,
∴
,
∴
,
故答案为;
20.
【解答】
解:根据题意:在中,有,
则(米).
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【解答】
解:(1)
;
(2)
.
22.
【解答】
解:∵
于,
∴
,
∵
,
∴
,
∴
.
23.
【解答】
解:如图,过点作,垂足为,
设海里.
在中,
∵
,
∴
,
在中,
∵
,
∴
.
∵
,
∴
,解得.
∵
,
∴
(海里).
∴
巡逻船与落水人的距离为海里.
24.
【解答】
解:(1)∵
垂直平分,
∴
,
∵
在中,,
∴
,
∴
,
∴
.
在中,,
∴
;
(2)设,则,
∵
在中,,,
∴
,,
∵
,
∴
,
∵
,
∴
.
∵
在中,,,
∴
.
25.
【解答】
解:∵
米,,
∴
过点作于点.则有为的中点,
即.
又据题意知垂直平分,
则,而米,
在中,,
.
又∵
,
∴
.
因而,在中,∵
,
∴
(米).
∵
,
∴
调整后的投影仪与投影幕布之间的距离符合要求.
26.
【解答】
解:如图所示:延长交于,
∵
,,
∴
,
∵
,
∴
设,则
在中,由勾股定理,
∵
,
∴
,
∴
,,
设,在中,,
∴
,
?,
∴
?;
∴
大厅层高为,
而,
∴
雕像放不下.
解直角三角形
单元检测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
在中,是直角,,那么的度数是(
)
A.
B.
C.
D.
?
2.
用计算器计算的结果(精确到)是(
)
A.
B.
C.
D.
?
3.
在中,=,如果=,,那么的长是(
)
A.
B.
C.
D.
?
4.
在中,=,若,则的值是(
)
A.
B.
C.
D.
?
5.
如图,某地修建高速公路,要从地向地修一座隧道(、在同一水平面上).为了测量、两地之间的距离,某工程师乘坐热气球从地出发,垂直上升到达处,在处观察地的俯角为,则、两地之间的距离为(
)
A.
B.
C.
D.
?
6.
海军军事演习中,有三艘船在同时刻向指挥所报告:船说船在它的正东方向,船在它的北偏东方向;船说船在它的北偏西方向;船说它在船的距离比它到船的距离远海里,则的距离为
A.海里
B.海里
C.海里
D.海里
?
7.
在一次数学活动中,李明利用一根栓有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度.如图,已知小明距假山的水平距离为,他的眼镜距地面的高度为,李明的视线经过量角器零刻度线和假山的最高点,此时,铅垂线经过量角器的刻度线,则假山的高度为(
)
A.
B.
C.
D.
?
8.
如图,小惠家(图中点处)门前有一条东西走向的公路,测得一水塔(图中点处),在她家北偏东方向米处,那么他所在位置到公路的距离为(
)米.
A.
B.
C.
D.
?
9.
中,,均为锐角,且,则一定是(
)
A.等腰三角形
B.等边三角形
C.直角三角形
D.有一个角是的三角形
?10.
如图,小明站在某广场一看台处,从眼睛处测得广场中心的俯角为,若=米,=米,平行于地面,台阶的坡度为=,坡长=米,则看台底端点距离广场中心点的距离约为(参考数据:,,)(
)
A.米
B.米
C.米
D.米
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
若,则________.
?
12.
在中,,,,则的值是________.
?
13.
如图,在塔前的平地上选择一点,测出塔顶的仰角为,从点向塔底走到达点,测出塔顶的仰角为,则塔的高为________.
?
14.
如图,一棵大树在一次强台风中于距地面米处倒下,则这棵树在折断前的高度为________米.
?
15.
如图,在中,,,于,则________度.
?
16.
在中,=,=,,则=________.
?
17.
小明在某风景区的观景台处观测到东北方向的处有一艘货船,该船正向南匀速航行,分钟后再观察时,该船已航行到的南偏东,且与相距的处.如图.货船的航行速度是________.(结果用根号表示)
?
18.
如图,在大楼的楼顶处测得另一栋楼底部的俯角为度,已知、两点间的距离为米,那么大楼的高度为________米.(结果保留根号)
?
19.
如图,在中,,,,是上的高,则的值是________.
?
20.
初三班研究学习小组为了测量学校旗杆的高度(如图),他们离旗杆底部点米的处,用测角仪测得旗杆的仰角为,已知测角仪器高米,则旗杆的高为________米(精确到米).
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
计算:
(1)
(2).
?
22.
如图,在中,,是延长线上一点,,垂足为,与相交于点,.求的度数.
?
23.
我南海巡逻船接到有人落水求救信号,如图,巡逻船观测到,同时,巡逻船观测到,两巡逻船相距海里,求此时巡逻船与落水人的距离?(参考数据:,,,)
?
24.
如图,在中,,的垂直平分线与,的交点分别为,.
(1)若,,求的长和的值;
(2)若,求的值.(结果保留根号)
?
25.
如图,某学校的教室多媒体投影仪正对投影幕布的中央,其距离米.为了方便课堂教学与使用,现将投影幕布由黑板正中的位置调整到左面的位置处,测得米,,此时投影仪调整到线段上的点处且恰好正对投影幕布的中央.若投影仪与投影幕布的安装距离控制在米到米之间礼堂效果最好,则调整后的投影仪与投影幕布之间的距离是否符合要求?(参考数据:,,,,可用科学计算器,结果精确到)
?
26.
重庆大坪时代天街已成为人们周末休闲娱乐的重要场所,时代天街从一楼到二楼有一自动扶梯(如图),图是侧面示意图.已知自动扶梯的坡度为,,是二楼楼顶,,是上处在自动扶梯顶端正上方的一点,且,在自动扶梯底端处测得点仰角为.
为了吸引顾客,开发商想在处放置一个高的《疯狂动物城》的装饰雕像,并要求雕像最高点与二楼顶层要留出距离好放置灯具,请问这个雕像能放得下吗?如果不能,请说明理由.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【解答】
解:.
故选.
2.
【解答】
解:用计算器解.
故选.
3.
【解答】
∵
,
∴
,
4.
【解答】
∵
=,即=,
∴
,
解得或(舍去),
∴
.
5.
【解答】
根据题意得:=,,=,
在中,.
6.
【解答】
解:,
∴
,即是直角三角形.
,
又∵
∴
解得:(海里)
故选.
7.
【解答】
解:∵
米,李明的眼睛高米,,
∴
,米,,
∴
,
解得(米),
即米.
故选:.
8.
【解答】
解:由已知得,,.
则.
故选.
9.
【解答】
∵
中,,均为锐角,且,
∴
或,
即或.
∴
或.
∴
有一个角是.
10.
【解答】
如图,作交的延长线于,延长交的延长线于.
∵
=,=米,
∴
=(米),=(米),
在中,,
∴
,
∴
(米),
∴
==(米),
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【解答】
解:∵
,
∴
.
故答案为:.
12.
【解答】
解:作于,如图,
∵
,
∴
,
在中,,
∵
,
∴
,
∵
,
∴
,
∴
,
在中,,
∴
.
故答案为.
13.
【解答】
解:在中,
∵
,
∴
.
在中,
∵
,
,
∴
.
设(米),
∵
,
∴
.
∴
,
∴
,
故答案为:
14.
【解答】
解:设树断处到顶部长,
∴
,
∴
.
∴
此树长.
15.
【解答】
解:∵
,
∴
,
∵
在中,,
∴
,
∴
.
故答案为:.
16.
【解答】
中,=,=,,得
===,
17.
【解答】
解:如图,在直角中,,,,
∴
,.
在直角中,,,,
∴
,
∴
,
∴
货船的航行速度是.
故答案为.
18.
【解答】
由题意得,=,=,=,
∴
,
∴
=,
19.
【解答】
解:∵
,,
∴
,
∴
,,
∴
,
∴
,
故答案为;
20.
【解答】
解:根据题意:在中,有,
则(米).
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【解答】
解:(1)
;
(2)
.
22.
【解答】
解:∵
于,
∴
,
∵
,
∴
,
∴
.
23.
【解答】
解:如图,过点作,垂足为,
设海里.
在中,
∵
,
∴
,
在中,
∵
,
∴
.
∵
,
∴
,解得.
∵
,
∴
(海里).
∴
巡逻船与落水人的距离为海里.
24.
【解答】
解:(1)∵
垂直平分,
∴
,
∵
在中,,
∴
,
∴
,
∴
.
在中,,
∴
;
(2)设,则,
∵
在中,,,
∴
,,
∵
,
∴
,
∵
,
∴
.
∵
在中,,,
∴
.
25.
【解答】
解:∵
米,,
∴
过点作于点.则有为的中点,
即.
又据题意知垂直平分,
则,而米,
在中,,
.
又∵
,
∴
.
因而,在中,∵
,
∴
(米).
∵
,
∴
调整后的投影仪与投影幕布之间的距离符合要求.
26.
【解答】
解:如图所示:延长交于,
∵
,,
∴
,
∵
,
∴
设,则
在中,由勾股定理,
∵
,
∴
,
∴
,,
设,在中,,
∴
,
?,
∴
?;
∴
大厅层高为,
而,
∴
雕像放不下.
