人教版九年级数学上册22.2 二次函数与一元二次方程 同步练习(Word版含答案)
文档属性
| 名称 | 人教版九年级数学上册22.2 二次函数与一元二次方程 同步练习(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 131.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 09:36:19 | ||
图片预览



文档简介
22.2
二次函数与一元二次方程
一.选择题
1.抛物线y=x2+bx+3的对称轴是直线x=1,若关于x的一元二次方程x2+bx+3﹣m=0(m为实数)在﹣1<x<2的范围内有实数根,则m的取值范围为( )
A.2≤m<6
B.m≥2
C.6<m<11
D.2≤m<11
2.已知二次函数y=ax2+bx+c的y与x的部分对应值如表:
x
﹣1
0
1
3
y
﹣3
1
3
1
下列结论:①抛物线的开口向下;②其图象的对称轴为直线x=1;③当x<2时,函数值y随x的增大而增大;④方程ax2+bx+c=0有一个根大于4.其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
3.已知y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=2.若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两个根,且x1<x2,﹣1<x1<0,则下列说法正确的是( )
A.x1+x2<0
B.4<x2<5
C.b2﹣4ac<0
D.ab>0
4.抛物线y=ax2+bx+c(a,b,c是常数,a≠0)经过点A(1,0)和点B(0,﹣2),且抛物线的对称轴在y轴的左侧.下列结论:①abc<0;②方程ax2+(b﹣1)x+c=0有两个不等的实数根;③﹣2<a﹣b<2.其中,正确结论的个数是( )
A.0
B.1
C.2
D.3
5.若抛物线y=ax2+bx+c(a>0)经过第四象限的点(1,﹣1),则关于x的方程ax2+bx+c=0的根的情况是( )
A.有两个大于1的不相等实数根
B.有两个小于1的不相等实数根
C.有一个大于1另一个小于1的实数根
D.没有实数根
6.已知二次函数y=ax2+bx+c的图象经过(﹣3,0)与(1,0)两点,关于x的方程ax2+bx+c+m=0(m>0)有两个根,其中一个根是3.则关于x的方程ax2+bx+c+n=0
(0<n<m)有两个整数根,这两个整数根是( )
A.﹣2或0
B.﹣4或2
C.﹣5或3
D.﹣6或4
7.二次函数y=x2+bx+c的部分对应值如下表:
x
…
﹣2
﹣1
0
1
2
4
…
y
…
5
0
﹣3
﹣4
﹣3
5
…
则关于x的一元二次方程x2+bx+c=0的解为( )
A.x1=﹣1,x2=﹣3
B.x1=﹣1,x2=1
C.x1=﹣1,x2=3
D.x1=﹣1,x2=5
8.已知二次函数y=ax2+bx+c的部分图象如图所示,则关于x的一元二次方程ax2+bx+c=0的解为( )
A.x1=﹣3,x2=0
B.x1=3,x2=﹣1
C.x=﹣3
D.x1=﹣3,x2=1
9.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
x
﹣1
0
1
3
y
﹣1
3
5
3
其中正确的结论是( )
A.抛物线开口向上
B.当x<1时,y的值随x值的增大而减小
C.当x=4时,y>0
D.方程ax2+bx+c=0的负根在﹣1与0之间
二.填空题
10.已知函数y=ax2+bx+c中,函数值与自变量的部分对应值如表,则方程ax2+bx+c=0的一个解的范围为:
.
x
……
2.41
2.54
2.67
2.75
……
y
……
﹣0.43
﹣0.17
0.12
0.32
……
11.根据下列表格中y=ax2+bx+c的自变量x与函数值y的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是
.
x
6.17
6.18
6.19
6.20
y=ax2+bx+c
﹣0.03
﹣0.01
0.02
0.04
三.解答题
12.已知二次函数y=x2﹣2mx+2m﹣1(m为常数).
(1)求证:不论m为何值,该函数图象与x轴一定有公共点;
(2)求证:不论m为何值,该函数图象的顶点都在函数y=﹣(x﹣1)2的图象上;
(3)已知点A(a,﹣1),B(a+2,﹣1),线段AB与函数y=﹣(x﹣1)2的图象有公共点,则a的取值范围是
.
13.借鉴我们已有的研究函数的经验,探索函数y=|x2﹣2x﹣3|﹣2的图象和性质,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如表:
x
…
﹣3
﹣2
﹣1
0
1
2
3
4
5
…
y
…
10
m
﹣2
1
n
1
﹣2
3
10
…
其中,m=
,n=
;
(2)根据如表数据,在如图所示的平面直角坐标系中描点,并画出函数图象;
(3)观察函数图象:
①在该平面直角坐标系中画出直线y=x+2的图象,根据图象直接写出该直线与函数y=|x2﹣2x﹣3|﹣2的交点横坐标x的范围:(哪两个连续整数之间);
②当方程|x2﹣2x﹣3|=b+2有且仅有四个不相等的实数根时,根据函数图象直接写出b的取值范围为
.
14.某“数学兴趣小组”根据学习函数的经验,对函数y=﹣x2+2|x|+1的图象和性质进行了探究.探究过程如下,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组时应数值如表:
x
…
﹣3
﹣
﹣2
﹣1
0
1
m
3
…
y
…
﹣2
﹣
n
2
1
2
1
﹣
﹣2
…
其中m=
,n=
;
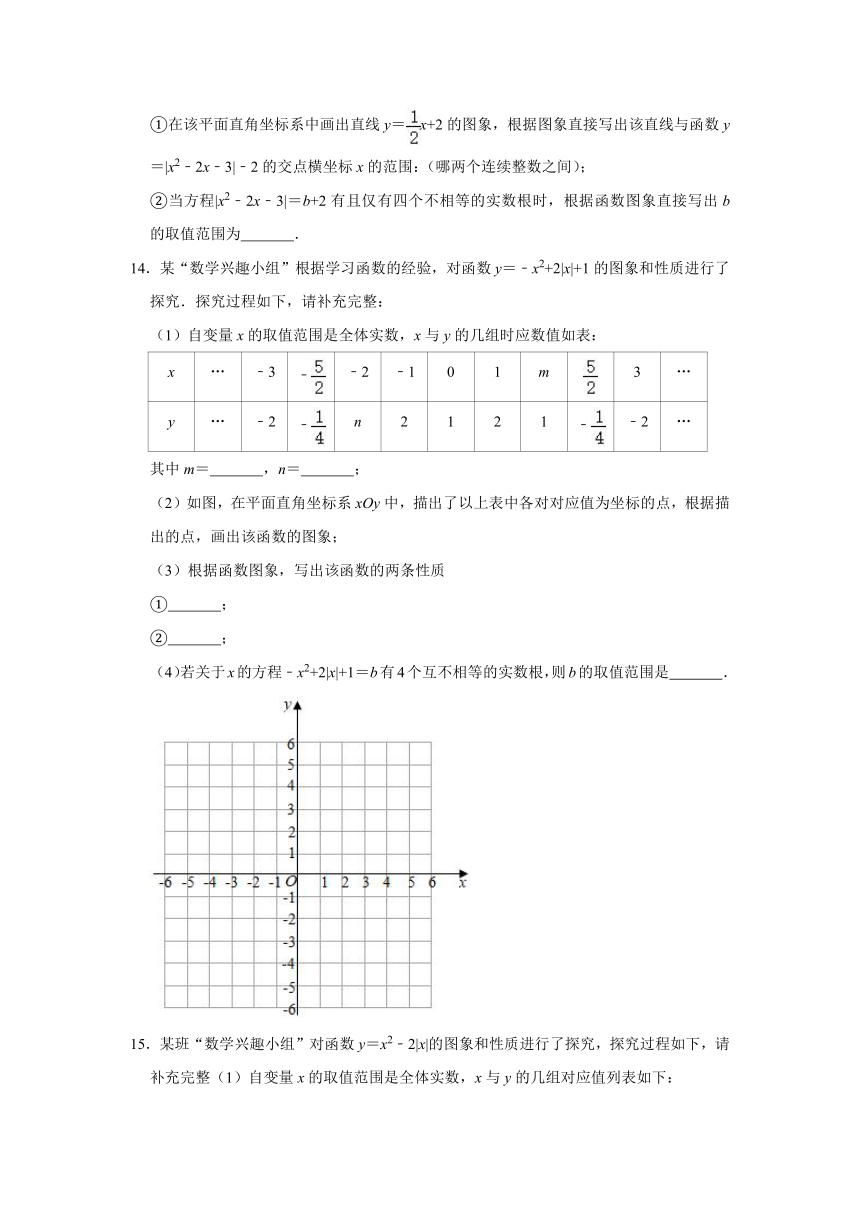
(2)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)根据函数图象,写出该函数的两条性质
①
;
②
;
(4)若关于x的方程﹣x2+2|x|+1=b有4个互不相等的实数根,则b的取值范围是
.
15.某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x
…
﹣3
﹣2.5
﹣2
﹣1
0
1
2
2.5
3
…
y
…
3
1.25
m
﹣1
0
﹣1
0
1.25
3
…
其中,m=
.
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出1条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有
个交点,所以对应的方程x2﹣2|x|=0有
个实数根;
②方程x2﹣2|x|=2有
个实数根.
③函数y=x2﹣2|x|的图象与y=a有至少有3个交点时,a的取值范围是
.
参考答案
一.选择题
1.
A.
2.
A.
3.
B.
4.
D.
5.
C.
6.
B.
7.
C.
8.
D.
9.
D.
二.填空题
10.
2.54~2.67.
11.
6.18<x<6.19.
三.解答题
12.(1)证明:∵△=4m2﹣4(2m﹣1)
=4m2﹣8m+4
=4(m﹣1)2≥0,
所以不论m为何值,该二次函数的图象与x轴总有公共点;
(2)证明:y=x2﹣2mx+2m﹣1=(x﹣m)2﹣(m﹣1)2,
二次函数y=x2﹣2mx+2m﹣1的顶点坐标为(m,﹣(m﹣1)2)
当x=m时,y=﹣(x﹣1)2=﹣(m﹣1)2,
所以不论m为何值,该二次函数的图象的顶点都在函数y=﹣(x﹣1)2的图象上;
(3)当y=﹣1时,y=﹣(x﹣1)2=﹣1,解得x1=0,x2=2,
当a+2≥0且a≤2时,线段AB与函数y=﹣(x﹣1)2的图象有公共点,
所以a的范围为﹣2≤a≤2.
故答案为﹣2≤a≤2.
13.解:(1)把x=﹣2代入y=|x2﹣2x﹣3|﹣2,得y=3,
∴m=3,
把x=1代入y=|x2﹣2x﹣3|﹣2,得y=2,
∴n=2,
故答案为:3,2;
(2)描点连线绘制如下函数图象:
(3)①在图上画出直线y=x+2,改直线与函数y=|x2﹣2x﹣3|﹣2的交点横坐标为大概为﹣1.8和4.1,
故x的范围大致为﹣2<x<5;
②由图象可知,当b=﹣2或b>2时,函数y=|x2﹣2x﹣3|﹣2图象与直线y=b有两个交点,
∵当方程|x2﹣2x﹣3|=b+2有且仅有两个不相等的实数根时,b=﹣2或b>2,
故答案为b=﹣2或b>2;
14.解:(1)当x=﹣2时,n=﹣(﹣2)2+2×|﹣2|+1=﹣4+4+1=1;
从表格看,函数关于y轴对称,则从函数对称性看,m=﹣2,
故答案为﹣2,1;
(2)根据表格数据描点连线绘制函数图象如下所示:
(3)①函数图象关于y轴对称,
②x>1时,y随x的增大而减小(答案不唯一);
故答案为:函数图象关于y轴对称,x>1时,y随x的增大而减小(答案不唯一);
(4)由函数图象知:∵关于x的方程﹣x2+2|x|+1=kx+b有4个互不相等的实数根,
∴b的取值范围是1<b<2.
故答案为:1<b<2.
15.解:(1)根据函数的对称性,m=0,
故答案为:0;
(2)描点画出如下函数图象:
(3)函数的最小值为﹣1;
x>1时,y随x的增大而增大(答案不唯一);
(4)①从图象上看函数与x轴有3个交点,故对应方程x2﹣2|x|=0有3个根,
故答案为:3,3;
②设y=x2﹣2|x|,从图象看y=2与y=x2﹣2|x|有两个交点;
故答案为:2;
③函数y=x2﹣2|x|的图象与y=a有至少有3个交点时,a的取值范围是﹣1<a≤0,
故答案为:﹣1<a≤0.
二次函数与一元二次方程
一.选择题
1.抛物线y=x2+bx+3的对称轴是直线x=1,若关于x的一元二次方程x2+bx+3﹣m=0(m为实数)在﹣1<x<2的范围内有实数根,则m的取值范围为( )
A.2≤m<6
B.m≥2
C.6<m<11
D.2≤m<11
2.已知二次函数y=ax2+bx+c的y与x的部分对应值如表:
x
﹣1
0
1
3
y
﹣3
1
3
1
下列结论:①抛物线的开口向下;②其图象的对称轴为直线x=1;③当x<2时,函数值y随x的增大而增大;④方程ax2+bx+c=0有一个根大于4.其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
3.已知y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=2.若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两个根,且x1<x2,﹣1<x1<0,则下列说法正确的是( )
A.x1+x2<0
B.4<x2<5
C.b2﹣4ac<0
D.ab>0
4.抛物线y=ax2+bx+c(a,b,c是常数,a≠0)经过点A(1,0)和点B(0,﹣2),且抛物线的对称轴在y轴的左侧.下列结论:①abc<0;②方程ax2+(b﹣1)x+c=0有两个不等的实数根;③﹣2<a﹣b<2.其中,正确结论的个数是( )
A.0
B.1
C.2
D.3
5.若抛物线y=ax2+bx+c(a>0)经过第四象限的点(1,﹣1),则关于x的方程ax2+bx+c=0的根的情况是( )
A.有两个大于1的不相等实数根
B.有两个小于1的不相等实数根
C.有一个大于1另一个小于1的实数根
D.没有实数根
6.已知二次函数y=ax2+bx+c的图象经过(﹣3,0)与(1,0)两点,关于x的方程ax2+bx+c+m=0(m>0)有两个根,其中一个根是3.则关于x的方程ax2+bx+c+n=0
(0<n<m)有两个整数根,这两个整数根是( )
A.﹣2或0
B.﹣4或2
C.﹣5或3
D.﹣6或4
7.二次函数y=x2+bx+c的部分对应值如下表:
x
…
﹣2
﹣1
0
1
2
4
…
y
…
5
0
﹣3
﹣4
﹣3
5
…
则关于x的一元二次方程x2+bx+c=0的解为( )
A.x1=﹣1,x2=﹣3
B.x1=﹣1,x2=1
C.x1=﹣1,x2=3
D.x1=﹣1,x2=5
8.已知二次函数y=ax2+bx+c的部分图象如图所示,则关于x的一元二次方程ax2+bx+c=0的解为( )
A.x1=﹣3,x2=0
B.x1=3,x2=﹣1
C.x=﹣3
D.x1=﹣3,x2=1
9.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表:
x
﹣1
0
1
3
y
﹣1
3
5
3
其中正确的结论是( )
A.抛物线开口向上
B.当x<1时,y的值随x值的增大而减小
C.当x=4时,y>0
D.方程ax2+bx+c=0的负根在﹣1与0之间
二.填空题
10.已知函数y=ax2+bx+c中,函数值与自变量的部分对应值如表,则方程ax2+bx+c=0的一个解的范围为:
.
x
……
2.41
2.54
2.67
2.75
……
y
……
﹣0.43
﹣0.17
0.12
0.32
……
11.根据下列表格中y=ax2+bx+c的自变量x与函数值y的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是
.
x
6.17
6.18
6.19
6.20
y=ax2+bx+c
﹣0.03
﹣0.01
0.02
0.04
三.解答题
12.已知二次函数y=x2﹣2mx+2m﹣1(m为常数).
(1)求证:不论m为何值,该函数图象与x轴一定有公共点;
(2)求证:不论m为何值,该函数图象的顶点都在函数y=﹣(x﹣1)2的图象上;
(3)已知点A(a,﹣1),B(a+2,﹣1),线段AB与函数y=﹣(x﹣1)2的图象有公共点,则a的取值范围是
.
13.借鉴我们已有的研究函数的经验,探索函数y=|x2﹣2x﹣3|﹣2的图象和性质,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如表:
x
…
﹣3
﹣2
﹣1
0
1
2
3
4
5
…
y
…
10
m
﹣2
1
n
1
﹣2
3
10
…
其中,m=
,n=
;
(2)根据如表数据,在如图所示的平面直角坐标系中描点,并画出函数图象;
(3)观察函数图象:
①在该平面直角坐标系中画出直线y=x+2的图象,根据图象直接写出该直线与函数y=|x2﹣2x﹣3|﹣2的交点横坐标x的范围:(哪两个连续整数之间);
②当方程|x2﹣2x﹣3|=b+2有且仅有四个不相等的实数根时,根据函数图象直接写出b的取值范围为
.
14.某“数学兴趣小组”根据学习函数的经验,对函数y=﹣x2+2|x|+1的图象和性质进行了探究.探究过程如下,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组时应数值如表:
x
…
﹣3
﹣
﹣2
﹣1
0
1
m
3
…
y
…
﹣2
﹣
n
2
1
2
1
﹣
﹣2
…
其中m=
,n=
;
(2)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)根据函数图象,写出该函数的两条性质
①
;
②
;
(4)若关于x的方程﹣x2+2|x|+1=b有4个互不相等的实数根,则b的取值范围是
.
15.某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x
…
﹣3
﹣2.5
﹣2
﹣1
0
1
2
2.5
3
…
y
…
3
1.25
m
﹣1
0
﹣1
0
1.25
3
…
其中,m=
.
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出1条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有
个交点,所以对应的方程x2﹣2|x|=0有
个实数根;
②方程x2﹣2|x|=2有
个实数根.
③函数y=x2﹣2|x|的图象与y=a有至少有3个交点时,a的取值范围是
.
参考答案
一.选择题
1.
A.
2.
A.
3.
B.
4.
D.
5.
C.
6.
B.
7.
C.
8.
D.
9.
D.
二.填空题
10.
2.54~2.67.
11.
6.18<x<6.19.
三.解答题
12.(1)证明:∵△=4m2﹣4(2m﹣1)
=4m2﹣8m+4
=4(m﹣1)2≥0,
所以不论m为何值,该二次函数的图象与x轴总有公共点;
(2)证明:y=x2﹣2mx+2m﹣1=(x﹣m)2﹣(m﹣1)2,
二次函数y=x2﹣2mx+2m﹣1的顶点坐标为(m,﹣(m﹣1)2)
当x=m时,y=﹣(x﹣1)2=﹣(m﹣1)2,
所以不论m为何值,该二次函数的图象的顶点都在函数y=﹣(x﹣1)2的图象上;
(3)当y=﹣1时,y=﹣(x﹣1)2=﹣1,解得x1=0,x2=2,
当a+2≥0且a≤2时,线段AB与函数y=﹣(x﹣1)2的图象有公共点,
所以a的范围为﹣2≤a≤2.
故答案为﹣2≤a≤2.
13.解:(1)把x=﹣2代入y=|x2﹣2x﹣3|﹣2,得y=3,
∴m=3,
把x=1代入y=|x2﹣2x﹣3|﹣2,得y=2,
∴n=2,
故答案为:3,2;
(2)描点连线绘制如下函数图象:
(3)①在图上画出直线y=x+2,改直线与函数y=|x2﹣2x﹣3|﹣2的交点横坐标为大概为﹣1.8和4.1,
故x的范围大致为﹣2<x<5;
②由图象可知,当b=﹣2或b>2时,函数y=|x2﹣2x﹣3|﹣2图象与直线y=b有两个交点,
∵当方程|x2﹣2x﹣3|=b+2有且仅有两个不相等的实数根时,b=﹣2或b>2,
故答案为b=﹣2或b>2;
14.解:(1)当x=﹣2时,n=﹣(﹣2)2+2×|﹣2|+1=﹣4+4+1=1;
从表格看,函数关于y轴对称,则从函数对称性看,m=﹣2,
故答案为﹣2,1;
(2)根据表格数据描点连线绘制函数图象如下所示:
(3)①函数图象关于y轴对称,
②x>1时,y随x的增大而减小(答案不唯一);
故答案为:函数图象关于y轴对称,x>1时,y随x的增大而减小(答案不唯一);
(4)由函数图象知:∵关于x的方程﹣x2+2|x|+1=kx+b有4个互不相等的实数根,
∴b的取值范围是1<b<2.
故答案为:1<b<2.
15.解:(1)根据函数的对称性,m=0,
故答案为:0;
(2)描点画出如下函数图象:
(3)函数的最小值为﹣1;
x>1时,y随x的增大而增大(答案不唯一);
(4)①从图象上看函数与x轴有3个交点,故对应方程x2﹣2|x|=0有3个根,
故答案为:3,3;
②设y=x2﹣2|x|,从图象看y=2与y=x2﹣2|x|有两个交点;
故答案为:2;
③函数y=x2﹣2|x|的图象与y=a有至少有3个交点时,a的取值范围是﹣1<a≤0,
故答案为:﹣1<a≤0.
同课章节目录
