人教版九年级数学上册24.1 圆的有关性质同步练习(Word版含答案)
文档属性
| 名称 | 人教版九年级数学上册24.1 圆的有关性质同步练习(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 231.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 08:14:19 | ||
图片预览


文档简介
24.1
圆的有关性质
一.选择题
1.如图,OA是⊙O的半径,B为OA上一点(且不与点O、A重合),过点B作OA的垂线交⊙O于点C.以OB、BC为边作矩形OBCD,连结BD.若BD=10,BC=8,则AB的长为( )
A.8
B.6
C.4
D.2
2.一个压路机的前轮直径是1.7米,如果前轮每分钟转动6周,那么这台压路机10分钟前进( )米.
A.51π
B.102π
C.153π
D.204π
3.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=( )cm.
A.8
B.5
C.3
D.2
4.如图,AB是⊙O的直径,弦CD⊥AB于点M,若CD=8cm,MB=2cm,则直径AB的长为( )
A.9
cm
B.10
cm
C.11
cm
D.12
cm
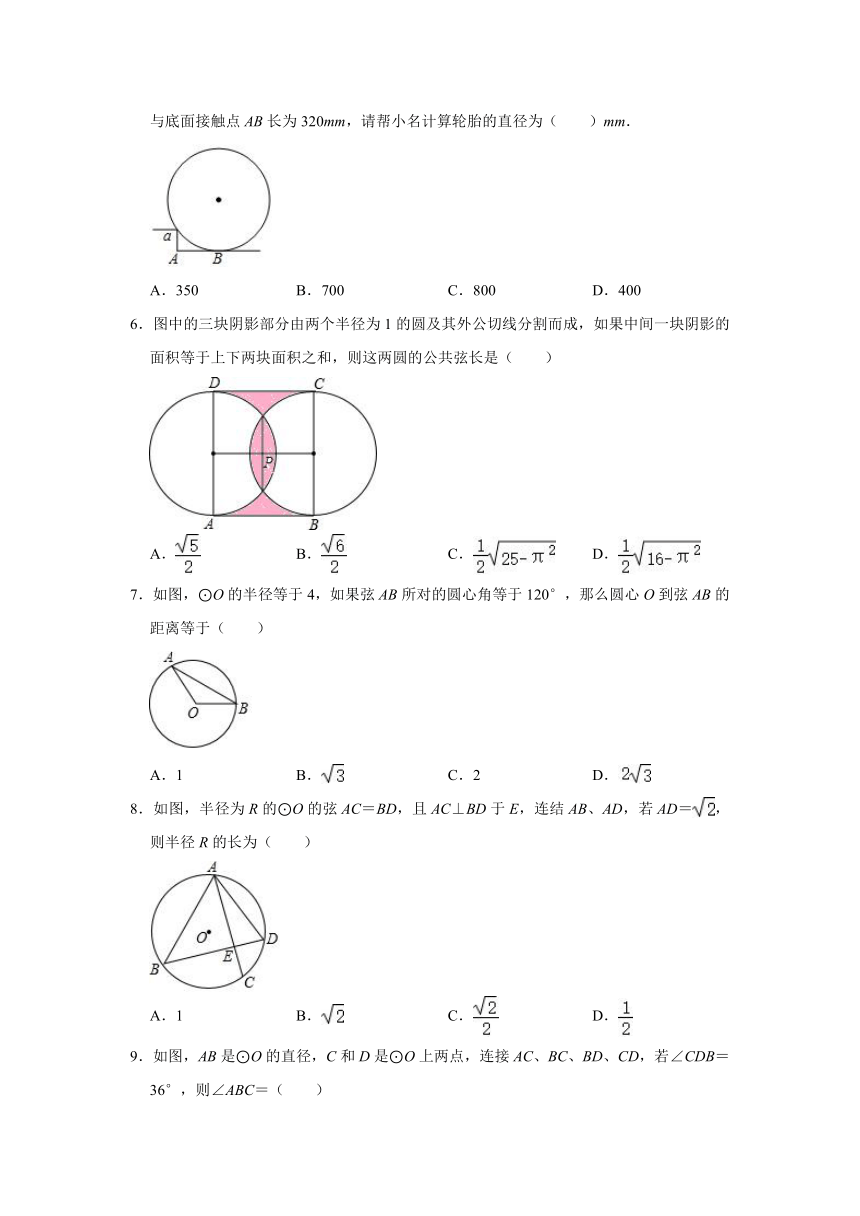
5.小名同学响应学习号召,在实际生活中发现问题,并利用所学的数学知识解决问题,他将汽车轮胎如图放置在地面台阶直角处,他测量了台阶高a为160mm,直角顶点到轮胎与底面接触点AB长为320mm,请帮小名计算轮胎的直径为( )mm.
A.350
B.700
C.800
D.400
6.图中的三块阴影部分由两个半径为1的圆及其外公切线分割而成,如果中间一块阴影的面积等于上下两块面积之和,则这两圆的公共弦长是( )
A.
B.
C.
D.
7.如图,⊙O的半径等于4,如果弦AB所对的圆心角等于120°,那么圆心O到弦AB的距离等于( )
A.1
B.
C.2
D.
8.如图,半径为R的⊙O的弦AC=BD,且AC⊥BD于E,连结AB、AD,若AD=,则半径R的长为( )
A.1
B.
C.
D.
9.如图,AB是⊙O的直径,C和D是⊙O上两点,连接AC、BC、BD、CD,若∠CDB=36°,则∠ABC=( )
A.36°
B.44°
C.54°
D.72°
10.如图所示,AB为⊙O的直径,点C在⊙O上,且OC⊥AB,过点C的弦CD与线段OB相交于点E,满足∠AEC=65°,连接AD,则∠BAD等于( )
A.20°
B.25°
C.30°
D.32.5°
11.如图,四边形ABCD内接于圆O,连接OB,OD,若∠BOD=∠BCD,则∠BAD的度数为( )
A.30°
B.45°
C.60°
D.120°
12.如图所示,四边形ABCD是圆O的内接四边形,∠A=45°,BC=4,CD=2,则弦BD的长为( )
A.2
B.3
C.
D.2
二.填空题
13.如图,⊙O的半径为6,△OAB的面积为18,点P为弦AB上一动点,当OP长为整数时,P点有
个.
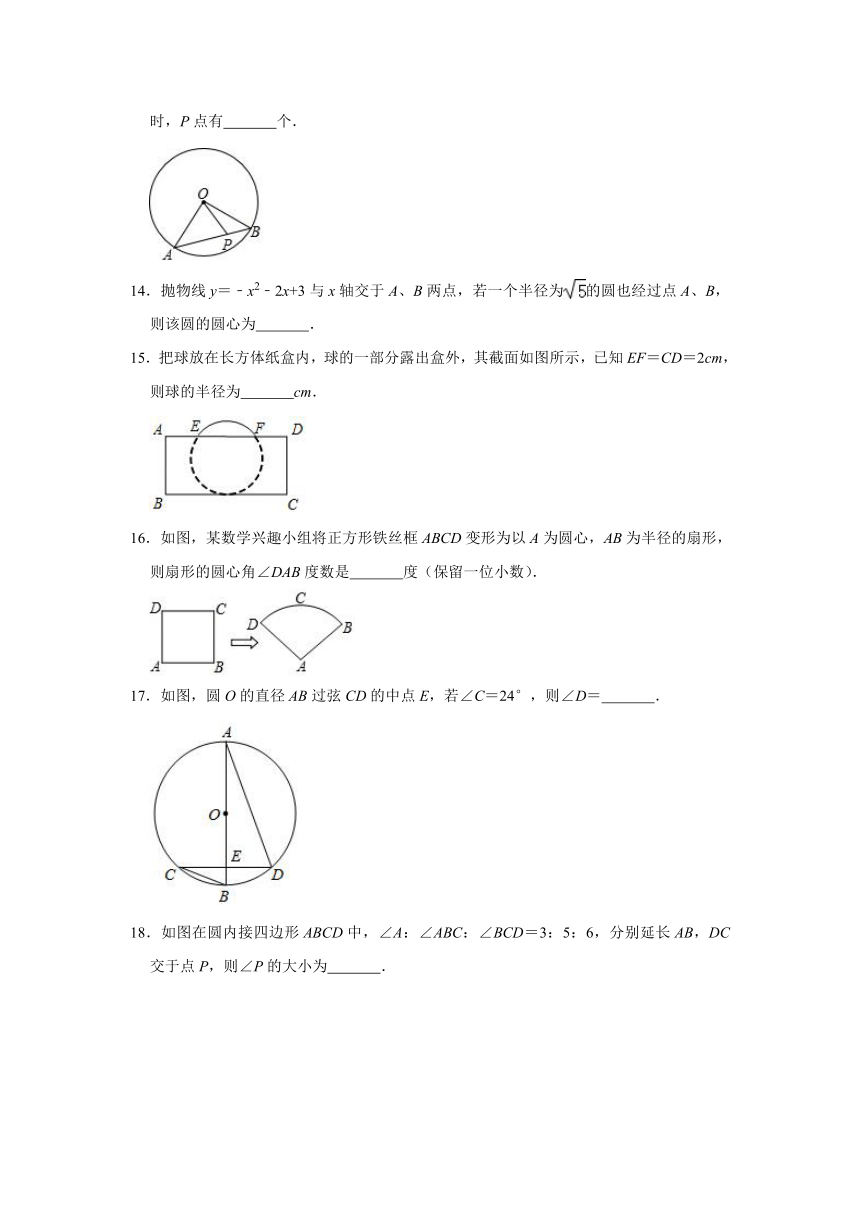
14.抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,若一个半径为的圆也经过点A、B,则该圆的圆心为
.
15.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=2cm,则球的半径为
cm.
16.如图,某数学兴趣小组将正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形,则扇形的圆心角∠DAB度数是
度(保留一位小数).
17.如图,圆O的直径AB过弦CD的中点E,若∠C=24°,则∠D=
.
18.如图在圆内接四边形ABCD中,∠A:∠ABC:∠BCD=3:5:6,分别延长AB,DC交于点P,则∠P的大小为
.
三.解答题
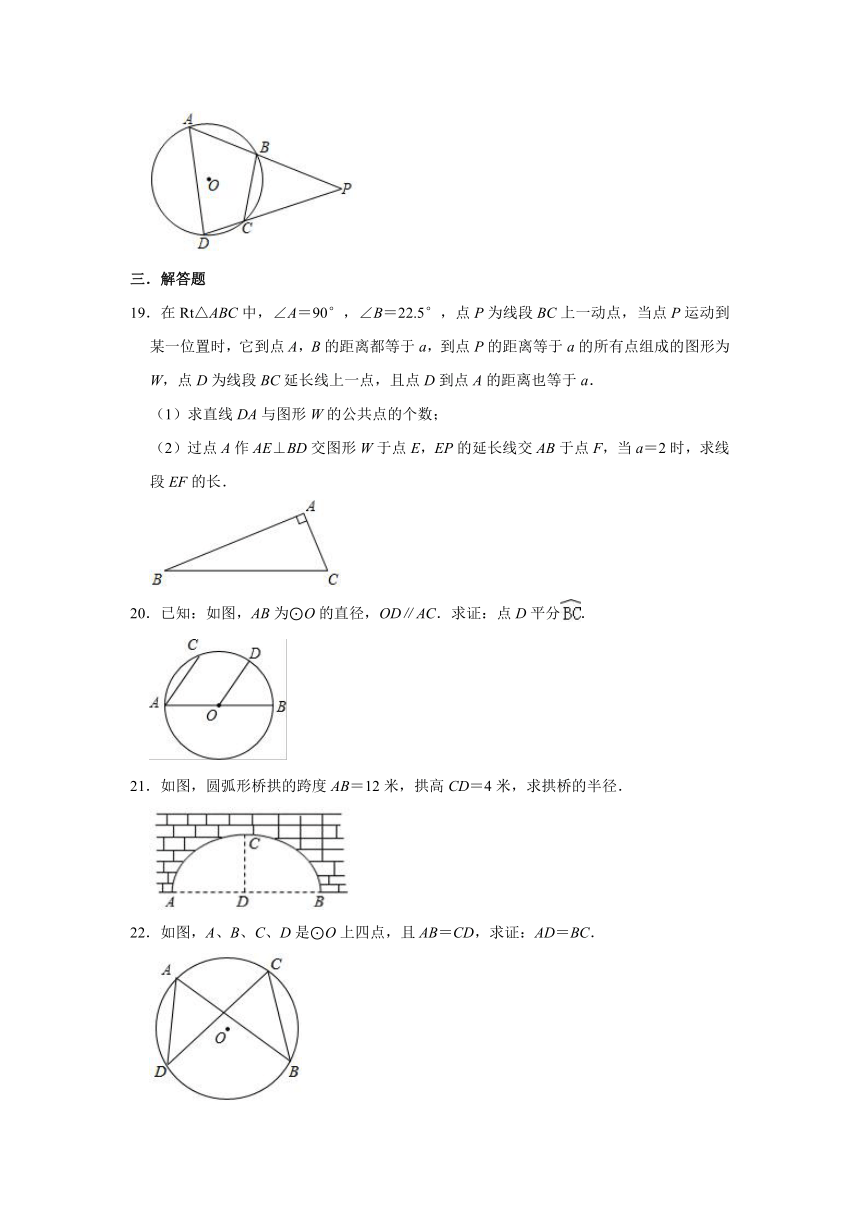
19.在Rt△ABC中,∠A=90°,∠B=22.5°,点P为线段BC上一动点,当点P运动到某一位置时,它到点A,B的距离都等于a,到点P的距离等于a的所有点组成的图形为W,点D为线段BC延长线上一点,且点D到点A的距离也等于a.
(1)求直线DA与图形W的公共点的个数;
(2)过点A作AE⊥BD交图形W于点E,EP的延长线交AB于点F,当a=2时,求线段EF的长.
20.已知:如图,AB为⊙O的直径,OD∥AC.求证:点D平分.
21.如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,求拱桥的半径.
22.如图,A、B、C、D是⊙O上四点,且AB=CD,求证:AD=BC.
23.如图,在△ABC中,AB=AC,BC为⊙O的直径,D为⊙O任意一点,连接AD交BC于点F,EA⊥AD交DB的延长线于E,连接CD.
(1)求证:△ABE≌△ACD;
(2)填空:①当∠CAD的度数为
时,四边形ABDC是正方形;
②若四边形ABDC的面积为4,则AD的长为
.
24.如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E.
(1)若∠BAC=40°,则∠ADC=
°;
(2)求证:∠BAC=2∠DAC;
(3)若AB=10,CD=5,求BC的值.
25.如图,在⊙O中,弦AD,BC相交于点E,连接OE,已知AD=BC,AD⊥CB.
(1)求证:AB=CD;
(2)如果⊙O的直径为10,DE=1,求AE的长.
参考答案
一.选择题
1.
C.
2.
B.
3.
A.
4.
B.
5.
C.
6.
D.
7.
C.
8.
A.
9.
C.
10.
A.
11.
C.
12.
D.
二.填空题
13.
4.
14.(﹣1,1)或(﹣1,﹣1).
15.
.
16.
114.6°.
17.
66°.
18.
40°.
三.解答题
19.解:(1)直线DA与图形W的公共点的个数为1个;
∵点P到点A,B的距离都等于a,
∴点P为AB的中垂线与BC的交点,
∵到点P的距离等于a的所有点组成图形W,
∴图形W是以点P为圆心,a为半径的圆,
根据题意补全图形如图所示,
连接AP,
∵∠B=22.5°,
∴∠APD=45°,
∵点D到点A的距离也等于a,
∴DA=AP=a,
∴∠D=∠APD=45°,
∴∠PAD=90°,
∴DA⊥PA,
∴DA为⊙P的切线,
∴直线DA与图形W的公共点的个数为1个;
(2)∵AP=BP,
∴∠BAP=∠B=22.5°,
∵∠BAC=90°,
∴∠PAC=∠PCA=67.5°,
∴PA=PC=a,
∴点C在⊙P上,
∵AE⊥BD交图形W于点E,
∴=,
∴AC=CE,
∴∠DPE=∠APD=45°,
∴∠APE=90°,
∵EP=AP=a=2,
∴AE=,∠E=45°,
∵∠B=22.5°,AE⊥BD,
∴∠BAE=67.5°,
∴∠AFE=∠BAE=67.5°.
∴EF=AE=.
20.证明:连接CB,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵OD∥AC,
∴∠OEB=∠ACB=90°,
即OD⊥BC,
∵OD过O,
∴点D平分.
21.解:根据垂径定理的推论,知此圆的圆心在CD所在的直线上,设圆心是O,
连接OA.根据垂径定理,得AD=6,
设圆的半径是r,根据勾股定理,得r2=36+(r﹣4)2,解得r=6.5,
答:拱桥的半径是6.5米.
22.证明:∵AB=CD,
∴=,
∴+=+,
∴=,
∴AD=BC.
23.(1)证明:∵BC为ΘO直径,
∴∠BAC=∠BDC=90°,
∴∠ABD+∠ACD=180°,
又∠ABD+∠ABE=180°,
∴∠ABE=∠ACD,
又∠BAF+∠CAF=∠BAF+∠BAE=90°,
∴∠CAF=∠BAE,
又AB=AC,
∴△ABE≌△ACD(ASA)
(2)解:①当∠CAD=45°时,四边形ABDC是正方形.
理由:∵∠CAD=∠BAD=45°,
∴=,
∴BD=CD,
∴△ABC,△BCD都是等腰直角三角形,
∵BC=BC,
∴△ABC≌△DBC(ASA),
∴AB=AC=BD=CD,
∴四边形ABDC是菱形,
∵∠BAC=90°,
∴四边形ABDC是正方形.
故答案为:45°.
②∵△EAB≌△DAC,
∴AE=AD,S△ABE=S△ADC,
∴S△AED=S四边形ABDC=4,
∴?AD2=4,
∴AD=2,
故答案为.
24.(1)解:∵AB=AC,∠BAC=40°,
∴∠ABC=∠ACB=70°,
∵四边形ABCD是⊙O的内接四边形,
∴∠ADC=180°﹣∠BAC=110°,
故答案为:110;
(2)证明:∵BD⊥AC,
∴∠AEB=∠BEC=90°,
∴∠ACB=90°﹣∠CBD,
∵AB=AC,
∴∠ABC=∠ACB=90°﹣∠CBD,
∴∠BAC=180°﹣2∠ABC=2∠CBD,
∵∠DAC=∠CBD,
∴∠BAC=2∠DAC;
(3)解:过A作AH⊥BC于H,
∵AB=AC,
∴∠BAH=∠CAH=CAB,CH=BH,
∵∠BAC=2∠DAC,
∴∠CAG=∠CAH,
过C作CG⊥AD交AD的延长线于G,
∴∠G=∠AHC=90°,
∵AC=AC,
∴△AGC≌△AHC(AAS),
∴AG=AH,CG=CH,
∵∠CDG=∠ABC,
∴△CDG∽△ABH,
∴==,
∴=,
设BH=k,AH=2k,
∴AB==k=10,
∴k=2,
∴BC=2k=4.
25.(1)证明:如图,∵AD=BC,
∴=,
∴﹣=﹣,即=,
∴AB=CD;
(2)如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.
则AF=FD,BG=CG.
∵AD=BC,
∴AF=CG.
在Rt△AOF与Rt△COG中,,
∴Rt△AOF≌Rt△COG(HL),
∴OF=OG,
∴四边形OFEG是正方形,
∴OF=EF.
设OF=EF=x,则AF=FD=x+1,
在直角△OAF中.由勾股定理得到:x2+(x+1)2=52,
解得
x=5.
则AF=3+1=4,即AE=AF+3=7.
圆的有关性质
一.选择题
1.如图,OA是⊙O的半径,B为OA上一点(且不与点O、A重合),过点B作OA的垂线交⊙O于点C.以OB、BC为边作矩形OBCD,连结BD.若BD=10,BC=8,则AB的长为( )
A.8
B.6
C.4
D.2
2.一个压路机的前轮直径是1.7米,如果前轮每分钟转动6周,那么这台压路机10分钟前进( )米.
A.51π
B.102π
C.153π
D.204π
3.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=( )cm.
A.8
B.5
C.3
D.2
4.如图,AB是⊙O的直径,弦CD⊥AB于点M,若CD=8cm,MB=2cm,则直径AB的长为( )
A.9
cm
B.10
cm
C.11
cm
D.12
cm
5.小名同学响应学习号召,在实际生活中发现问题,并利用所学的数学知识解决问题,他将汽车轮胎如图放置在地面台阶直角处,他测量了台阶高a为160mm,直角顶点到轮胎与底面接触点AB长为320mm,请帮小名计算轮胎的直径为( )mm.
A.350
B.700
C.800
D.400
6.图中的三块阴影部分由两个半径为1的圆及其外公切线分割而成,如果中间一块阴影的面积等于上下两块面积之和,则这两圆的公共弦长是( )
A.
B.
C.
D.
7.如图,⊙O的半径等于4,如果弦AB所对的圆心角等于120°,那么圆心O到弦AB的距离等于( )
A.1
B.
C.2
D.
8.如图,半径为R的⊙O的弦AC=BD,且AC⊥BD于E,连结AB、AD,若AD=,则半径R的长为( )
A.1
B.
C.
D.
9.如图,AB是⊙O的直径,C和D是⊙O上两点,连接AC、BC、BD、CD,若∠CDB=36°,则∠ABC=( )
A.36°
B.44°
C.54°
D.72°
10.如图所示,AB为⊙O的直径,点C在⊙O上,且OC⊥AB,过点C的弦CD与线段OB相交于点E,满足∠AEC=65°,连接AD,则∠BAD等于( )
A.20°
B.25°
C.30°
D.32.5°
11.如图,四边形ABCD内接于圆O,连接OB,OD,若∠BOD=∠BCD,则∠BAD的度数为( )
A.30°
B.45°
C.60°
D.120°
12.如图所示,四边形ABCD是圆O的内接四边形,∠A=45°,BC=4,CD=2,则弦BD的长为( )
A.2
B.3
C.
D.2
二.填空题
13.如图,⊙O的半径为6,△OAB的面积为18,点P为弦AB上一动点,当OP长为整数时,P点有
个.
14.抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,若一个半径为的圆也经过点A、B,则该圆的圆心为
.
15.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=2cm,则球的半径为
cm.
16.如图,某数学兴趣小组将正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形,则扇形的圆心角∠DAB度数是
度(保留一位小数).
17.如图,圆O的直径AB过弦CD的中点E,若∠C=24°,则∠D=
.
18.如图在圆内接四边形ABCD中,∠A:∠ABC:∠BCD=3:5:6,分别延长AB,DC交于点P,则∠P的大小为
.
三.解答题
19.在Rt△ABC中,∠A=90°,∠B=22.5°,点P为线段BC上一动点,当点P运动到某一位置时,它到点A,B的距离都等于a,到点P的距离等于a的所有点组成的图形为W,点D为线段BC延长线上一点,且点D到点A的距离也等于a.
(1)求直线DA与图形W的公共点的个数;
(2)过点A作AE⊥BD交图形W于点E,EP的延长线交AB于点F,当a=2时,求线段EF的长.
20.已知:如图,AB为⊙O的直径,OD∥AC.求证:点D平分.
21.如图,圆弧形桥拱的跨度AB=12米,拱高CD=4米,求拱桥的半径.
22.如图,A、B、C、D是⊙O上四点,且AB=CD,求证:AD=BC.
23.如图,在△ABC中,AB=AC,BC为⊙O的直径,D为⊙O任意一点,连接AD交BC于点F,EA⊥AD交DB的延长线于E,连接CD.
(1)求证:△ABE≌△ACD;
(2)填空:①当∠CAD的度数为
时,四边形ABDC是正方形;
②若四边形ABDC的面积为4,则AD的长为
.
24.如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E.
(1)若∠BAC=40°,则∠ADC=
°;
(2)求证:∠BAC=2∠DAC;
(3)若AB=10,CD=5,求BC的值.
25.如图,在⊙O中,弦AD,BC相交于点E,连接OE,已知AD=BC,AD⊥CB.
(1)求证:AB=CD;
(2)如果⊙O的直径为10,DE=1,求AE的长.
参考答案
一.选择题
1.
C.
2.
B.
3.
A.
4.
B.
5.
C.
6.
D.
7.
C.
8.
A.
9.
C.
10.
A.
11.
C.
12.
D.
二.填空题
13.
4.
14.(﹣1,1)或(﹣1,﹣1).
15.
.
16.
114.6°.
17.
66°.
18.
40°.
三.解答题
19.解:(1)直线DA与图形W的公共点的个数为1个;
∵点P到点A,B的距离都等于a,
∴点P为AB的中垂线与BC的交点,
∵到点P的距离等于a的所有点组成图形W,
∴图形W是以点P为圆心,a为半径的圆,
根据题意补全图形如图所示,
连接AP,
∵∠B=22.5°,
∴∠APD=45°,
∵点D到点A的距离也等于a,
∴DA=AP=a,
∴∠D=∠APD=45°,
∴∠PAD=90°,
∴DA⊥PA,
∴DA为⊙P的切线,
∴直线DA与图形W的公共点的个数为1个;
(2)∵AP=BP,
∴∠BAP=∠B=22.5°,
∵∠BAC=90°,
∴∠PAC=∠PCA=67.5°,
∴PA=PC=a,
∴点C在⊙P上,
∵AE⊥BD交图形W于点E,
∴=,
∴AC=CE,
∴∠DPE=∠APD=45°,
∴∠APE=90°,
∵EP=AP=a=2,
∴AE=,∠E=45°,
∵∠B=22.5°,AE⊥BD,
∴∠BAE=67.5°,
∴∠AFE=∠BAE=67.5°.
∴EF=AE=.
20.证明:连接CB,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵OD∥AC,
∴∠OEB=∠ACB=90°,
即OD⊥BC,
∵OD过O,
∴点D平分.
21.解:根据垂径定理的推论,知此圆的圆心在CD所在的直线上,设圆心是O,
连接OA.根据垂径定理,得AD=6,
设圆的半径是r,根据勾股定理,得r2=36+(r﹣4)2,解得r=6.5,
答:拱桥的半径是6.5米.
22.证明:∵AB=CD,
∴=,
∴+=+,
∴=,
∴AD=BC.
23.(1)证明:∵BC为ΘO直径,
∴∠BAC=∠BDC=90°,
∴∠ABD+∠ACD=180°,
又∠ABD+∠ABE=180°,
∴∠ABE=∠ACD,
又∠BAF+∠CAF=∠BAF+∠BAE=90°,
∴∠CAF=∠BAE,
又AB=AC,
∴△ABE≌△ACD(ASA)
(2)解:①当∠CAD=45°时,四边形ABDC是正方形.
理由:∵∠CAD=∠BAD=45°,
∴=,
∴BD=CD,
∴△ABC,△BCD都是等腰直角三角形,
∵BC=BC,
∴△ABC≌△DBC(ASA),
∴AB=AC=BD=CD,
∴四边形ABDC是菱形,
∵∠BAC=90°,
∴四边形ABDC是正方形.
故答案为:45°.
②∵△EAB≌△DAC,
∴AE=AD,S△ABE=S△ADC,
∴S△AED=S四边形ABDC=4,
∴?AD2=4,
∴AD=2,
故答案为.
24.(1)解:∵AB=AC,∠BAC=40°,
∴∠ABC=∠ACB=70°,
∵四边形ABCD是⊙O的内接四边形,
∴∠ADC=180°﹣∠BAC=110°,
故答案为:110;
(2)证明:∵BD⊥AC,
∴∠AEB=∠BEC=90°,
∴∠ACB=90°﹣∠CBD,
∵AB=AC,
∴∠ABC=∠ACB=90°﹣∠CBD,
∴∠BAC=180°﹣2∠ABC=2∠CBD,
∵∠DAC=∠CBD,
∴∠BAC=2∠DAC;
(3)解:过A作AH⊥BC于H,
∵AB=AC,
∴∠BAH=∠CAH=CAB,CH=BH,
∵∠BAC=2∠DAC,
∴∠CAG=∠CAH,
过C作CG⊥AD交AD的延长线于G,
∴∠G=∠AHC=90°,
∵AC=AC,
∴△AGC≌△AHC(AAS),
∴AG=AH,CG=CH,
∵∠CDG=∠ABC,
∴△CDG∽△ABH,
∴==,
∴=,
设BH=k,AH=2k,
∴AB==k=10,
∴k=2,
∴BC=2k=4.
25.(1)证明:如图,∵AD=BC,
∴=,
∴﹣=﹣,即=,
∴AB=CD;
(2)如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.
则AF=FD,BG=CG.
∵AD=BC,
∴AF=CG.
在Rt△AOF与Rt△COG中,,
∴Rt△AOF≌Rt△COG(HL),
∴OF=OG,
∴四边形OFEG是正方形,
∴OF=EF.
设OF=EF=x,则AF=FD=x+1,
在直角△OAF中.由勾股定理得到:x2+(x+1)2=52,
解得
x=5.
则AF=3+1=4,即AE=AF+3=7.
同课章节目录
