七年级数学下册教学课件-10.1.3 画轴对称图形1-华东师大版(共20张ppt)
文档属性
| 名称 | 七年级数学下册教学课件-10.1.3 画轴对称图形1-华东师大版(共20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 467.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 15:22:03 | ||
图片预览




文档简介
(共20张PPT)
画轴对称图形
试试你的眼力,判断下列图形哪些是轴对称图形,是轴对称图形的请指出其对称轴(认真,仔细)
A
B
D
C
预 习 部 分
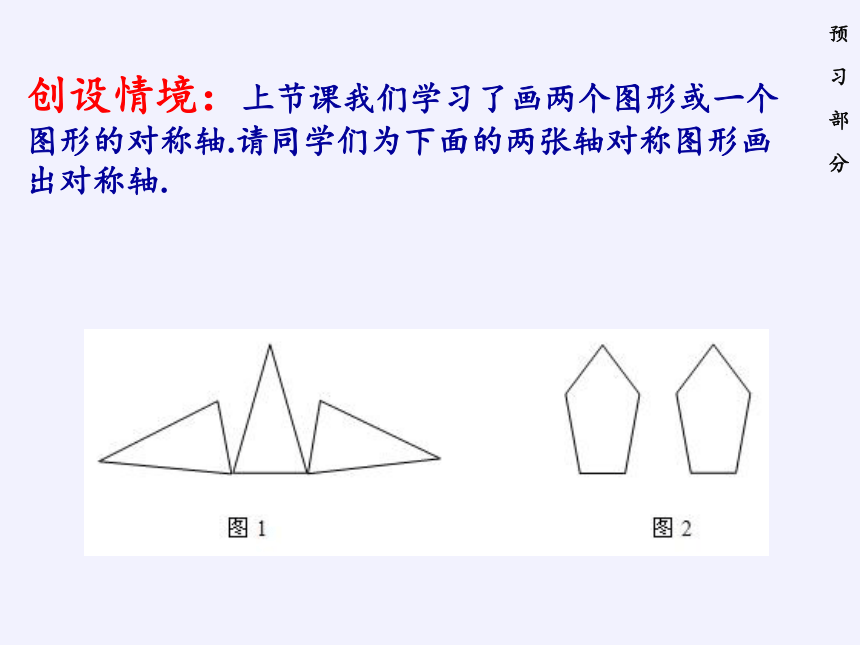
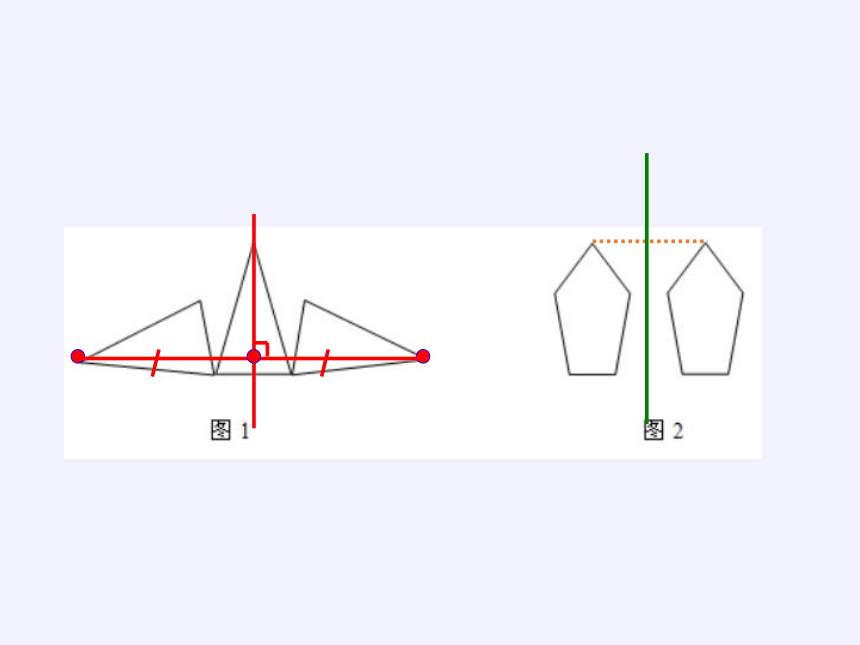
创设情境:上节课我们学习了画两个图形或一个图形的对称轴.请同学们为下面的两张轴对称图形画出对称轴.
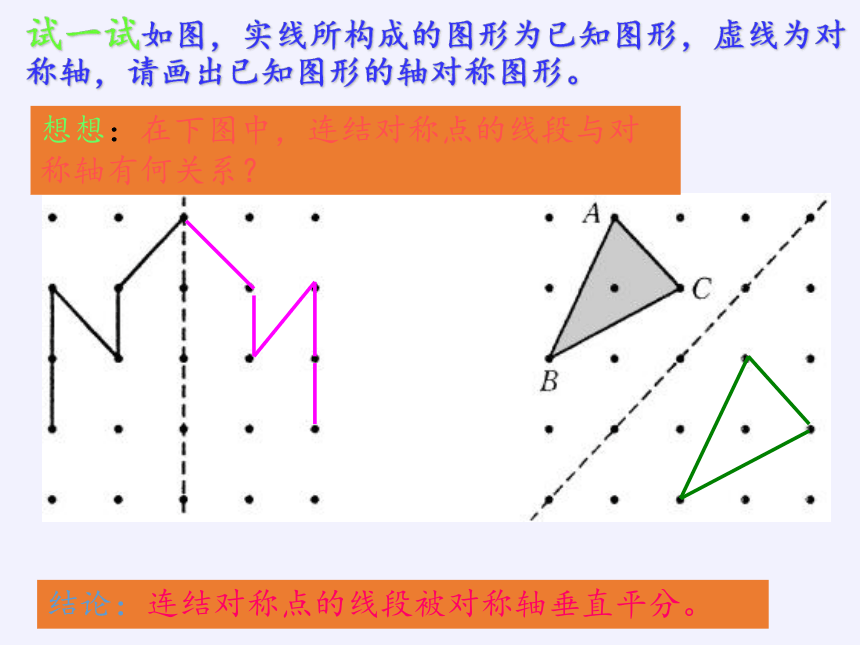
试一试如图,实线所构成的图形为已知图形,虚线为对称轴,请画出已知图形的轴对称图形。
想想:在下图中,连结对称点的线段与对称轴有何关系?
结论:连结对称点的线段被对称轴垂直平分。
想一想:如图,实线所构成的图形为已知图形,直线L为对称轴,没有格点又如何画已知图形的轴对称图形?
E
A
C
A
C
D
B
B
L
L
思路:把整个图形转化为多条线段,再将每条线段转化为两个端点。
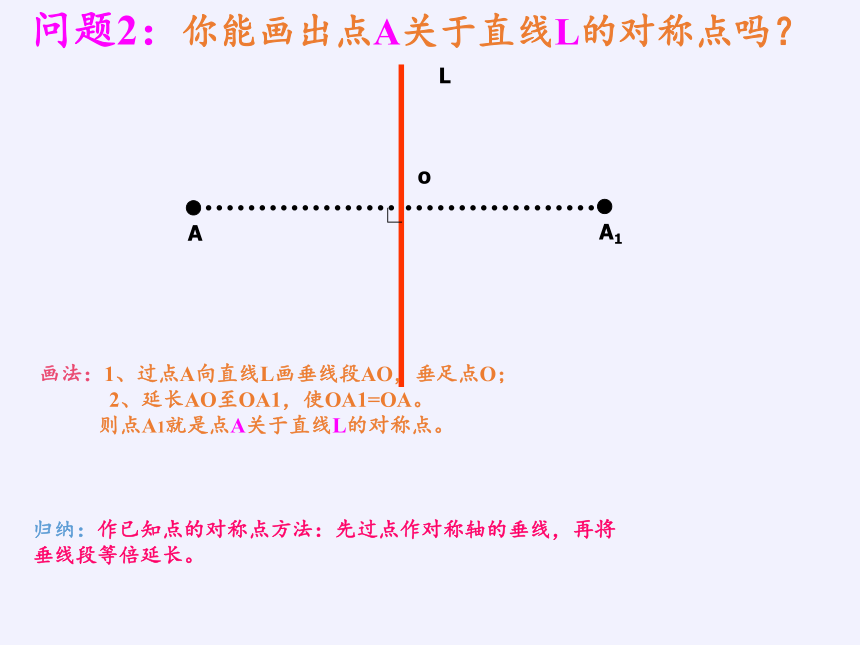
问题2:你能画出点A关于直线L的对称点吗?
A1
A
L
o
画法:1、过点A向直线L画垂线段AO,垂足点O;
2、延长AO至OA1,使OA1=OA。
则点A1就是点A关于直线L的对称点。
归纳:作已知点的对称点方法:先过点作对称轴的垂线,再将
垂线段等倍延长。
问题3:你能画出线段AB关于直线L的对称线段吗?
画法:
1、画点A、点B关于直线L的对称点A1
、B1;
A1
B1
B
A
L
2、连结A1
、B1
。
则线段A1
B1就是线段AB关于直线L的对称线段
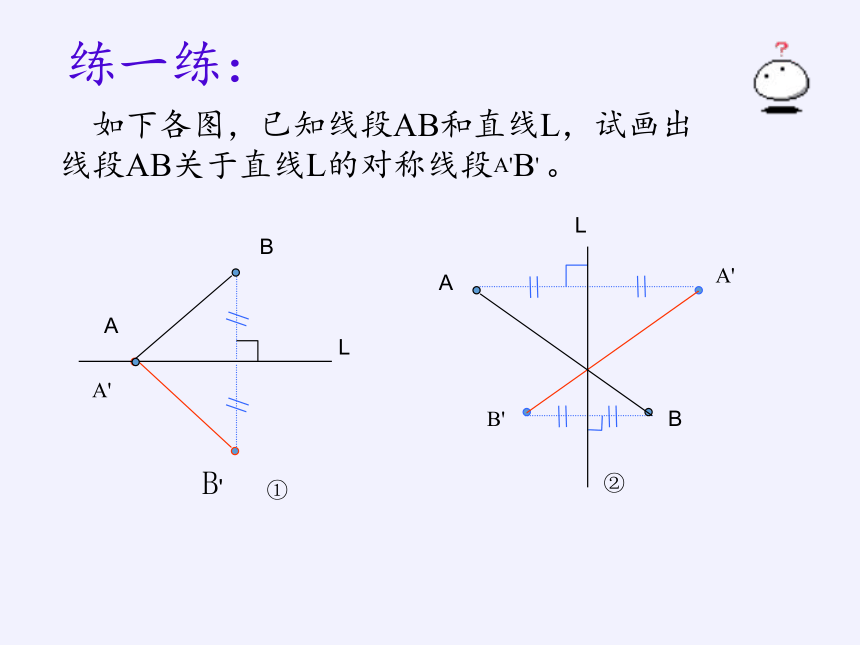
练一练:
如下各图,已知线段AB和直线L,试画出线段AB关于直线L的对称线段A'B'
。
B'
A'
A'
A
L
②
B
B'
①
L
A
B
问题4:你能画出三角形ABC关于直线L的对称图形吗?
C
B
A
A1
B1
C1
画法:
1、画出点A、点B和C点关于直线L的对称点A1
、
B1和C1。
2、连结A1
B1、
B1
C1
、A1
C1
、则
A1
B1
C1就是
AB
C关于直线L的对称三角形。
图形变式:
A
'
B
'
C
'
A
'
L
B
A
C
B
'
C
'
已知△ABC,直线L,画出△ABC关于直线L对称的图形。
B
A
C
L
2.在图中分别画出点A关于两条直线的对称点
A'和A''。
A
·
第2题
·
A''
·
A'
1.判断下列画线段MN的轴对称图形,哪一个是正确的(
)
A
B
C
D
N1
M
N
(M1)
M
N
M1
(N1)
M
N
N1
(M1)
以上答案都不对
练习题:
C
例1.以AB为对称轴,画出图形的对称图形.
解:作法1.作点D、C、E、F、G关于直线AB的对称点,
2.将所作的对称点顺次连接。
图形D1C1E1F1G1即为所作的对称图形。
D1
C1
E1
F1
G1
M′
例2:如下图,草原上两个居民点A、B在河流的同旁.一汽车从点A出发到B,途中需要到河边加水.汽车在哪一点加水,可使行驶的路程最短?在图中作出该处,并说明理由;在图上画出这点。
A
B
理由:在CD上任取一点M′,连结AM、AM′、A′M′、BM′
直线CD是A、A′的对称轴,M、M′在CD上,
∴AM=A′M,AM′=A′M′∴AM+BM=A′M+BM=A′B
在△A′M′B中∵A′M′+BM′>A′B(三角形两边之和大于第三边)
∴A′M′+BM′>AM+BM即AM+BM最小.
A′
河
M
C
D
E
解:已知:直线CD和CD同侧两点A、B.
求作:CD上一点M,使AM+BM最小.
作法:①作点A关于CD的对称点A’
②连结A’B交CD于点M
则点M即为所求的点.
例3:如图,M是∠AOB内部一点.
(1)分别作出M关于OA、OB的对称点M1,M2,连
结M1M2,交OA于点P,交OB于Q.(补全图形)
(2)若M1M2=10cm,求△MPQ的周长.
A
B
O
M
M1
M2
P
Q
解:1.作图见图形。
2.连接PM、QM
由作图可得:PA是MM1的对称轴
QB
为MM2
的对称轴
所以有PM=PM1,QM=QM2
所以PM+PQ+QM=
M1+PQ+QM2
因为M1+PQ+QM2=M1M2=10
所以PM+PQ+QM==10
例4:如图,在正方形网络上有一个△ABC.
(1)作△ABC关于直线MN的对称图形;
(2)若网络上的最小正方形的边长为1,求S△ABC.
A
B
C
M
N
A1
B1
C1
解(1)作法:
1.作点A、B、C的对称点;
2.将所作的对称点顺次连接;
图形A1B1C1为所作的对称图形。
(2)如图:
S四边形CDEF=2×3=6
S⊿ADC=1×3/2=1.5
S⊿AEB=1×2/2=1
S⊿ADC=1×2/2=1
所以,
S⊿ABC=
S四边形CDEF-
S⊿ADC-
S⊿AEB-
S⊿ADC
=
6
–
1.5
–
1
–
1
=
2.5
E
F
D
一面镜子竖直悬挂在墙上,人眼位置如图所示,有三个物体放在镜子面前,人眼能从镜子中看见哪个物体?
C1
B1
A1
B
O
A
C
M
N
●
探索创新题
一.要点:
1.画轴对称图形是因为已知图形是整个图形的一半。
2.因为整个图形是轴对称图形,所以要作的那一半与已知图形是轴对称关系.
3.画轴对称图形的基础:作已知图形特殊点的对称点。
4.思路:把整个图形转化为多条线段,再将每条线段转化为两个端点。
二.画已知图形关于直线的轴对称图形的方法
(1)先标出特殊点
(2)逐个画出特殊点的对称点
(3)连结这些对称点
三.注意:
(1)图形用实线,其他的线可以用虚线.
(2)作垂直时要画准,等倍延长垂线段要画对.
(3)要找准各对称点.
课
堂
小
结
作
业
1.
如图是由三个小正方形组成的图形,若在图中补画一个小正方形,使它成为轴对称图形,有几种画法?然后画出图形。
2.如图所示,钱塘江的一侧有A,B两个村庄现要在江边建造一个水厂C,把水送到这两个村庄,(1)要使供水管到两村庄的距离相等,水厂C应建在何处.(2)要使供水管路线最短,水厂C应建在何处,这样可以节省成本.
.A
.B
3.已知△ABC与直线l。画出△ABC关于直线l的对称图形.
谢
谢
画轴对称图形
试试你的眼力,判断下列图形哪些是轴对称图形,是轴对称图形的请指出其对称轴(认真,仔细)
A
B
D
C
预 习 部 分
创设情境:上节课我们学习了画两个图形或一个图形的对称轴.请同学们为下面的两张轴对称图形画出对称轴.
试一试如图,实线所构成的图形为已知图形,虚线为对称轴,请画出已知图形的轴对称图形。
想想:在下图中,连结对称点的线段与对称轴有何关系?
结论:连结对称点的线段被对称轴垂直平分。
想一想:如图,实线所构成的图形为已知图形,直线L为对称轴,没有格点又如何画已知图形的轴对称图形?
E
A
C
A
C
D
B
B
L
L
思路:把整个图形转化为多条线段,再将每条线段转化为两个端点。
问题2:你能画出点A关于直线L的对称点吗?
A1
A
L
o
画法:1、过点A向直线L画垂线段AO,垂足点O;
2、延长AO至OA1,使OA1=OA。
则点A1就是点A关于直线L的对称点。
归纳:作已知点的对称点方法:先过点作对称轴的垂线,再将
垂线段等倍延长。
问题3:你能画出线段AB关于直线L的对称线段吗?
画法:
1、画点A、点B关于直线L的对称点A1
、B1;
A1
B1
B
A
L
2、连结A1
、B1
。
则线段A1
B1就是线段AB关于直线L的对称线段
练一练:
如下各图,已知线段AB和直线L,试画出线段AB关于直线L的对称线段A'B'
。
B'
A'
A'
A
L
②
B
B'
①
L
A
B
问题4:你能画出三角形ABC关于直线L的对称图形吗?
C
B
A
A1
B1
C1
画法:
1、画出点A、点B和C点关于直线L的对称点A1
、
B1和C1。
2、连结A1
B1、
B1
C1
、A1
C1
、则
A1
B1
C1就是
AB
C关于直线L的对称三角形。
图形变式:
A
'
B
'
C
'
A
'
L
B
A
C
B
'
C
'
已知△ABC,直线L,画出△ABC关于直线L对称的图形。
B
A
C
L
2.在图中分别画出点A关于两条直线的对称点
A'和A''。
A
·
第2题
·
A''
·
A'
1.判断下列画线段MN的轴对称图形,哪一个是正确的(
)
A
B
C
D
N1
M
N
(M1)
M
N
M1
(N1)
M
N
N1
(M1)
以上答案都不对
练习题:
C
例1.以AB为对称轴,画出图形的对称图形.
解:作法1.作点D、C、E、F、G关于直线AB的对称点,
2.将所作的对称点顺次连接。
图形D1C1E1F1G1即为所作的对称图形。
D1
C1
E1
F1
G1
M′
例2:如下图,草原上两个居民点A、B在河流的同旁.一汽车从点A出发到B,途中需要到河边加水.汽车在哪一点加水,可使行驶的路程最短?在图中作出该处,并说明理由;在图上画出这点。
A
B
理由:在CD上任取一点M′,连结AM、AM′、A′M′、BM′
直线CD是A、A′的对称轴,M、M′在CD上,
∴AM=A′M,AM′=A′M′∴AM+BM=A′M+BM=A′B
在△A′M′B中∵A′M′+BM′>A′B(三角形两边之和大于第三边)
∴A′M′+BM′>AM+BM即AM+BM最小.
A′
河
M
C
D
E
解:已知:直线CD和CD同侧两点A、B.
求作:CD上一点M,使AM+BM最小.
作法:①作点A关于CD的对称点A’
②连结A’B交CD于点M
则点M即为所求的点.
例3:如图,M是∠AOB内部一点.
(1)分别作出M关于OA、OB的对称点M1,M2,连
结M1M2,交OA于点P,交OB于Q.(补全图形)
(2)若M1M2=10cm,求△MPQ的周长.
A
B
O
M
M1
M2
P
Q
解:1.作图见图形。
2.连接PM、QM
由作图可得:PA是MM1的对称轴
QB
为MM2
的对称轴
所以有PM=PM1,QM=QM2
所以PM+PQ+QM=
M1+PQ+QM2
因为M1+PQ+QM2=M1M2=10
所以PM+PQ+QM==10
例4:如图,在正方形网络上有一个△ABC.
(1)作△ABC关于直线MN的对称图形;
(2)若网络上的最小正方形的边长为1,求S△ABC.
A
B
C
M
N
A1
B1
C1
解(1)作法:
1.作点A、B、C的对称点;
2.将所作的对称点顺次连接;
图形A1B1C1为所作的对称图形。
(2)如图:
S四边形CDEF=2×3=6
S⊿ADC=1×3/2=1.5
S⊿AEB=1×2/2=1
S⊿ADC=1×2/2=1
所以,
S⊿ABC=
S四边形CDEF-
S⊿ADC-
S⊿AEB-
S⊿ADC
=
6
–
1.5
–
1
–
1
=
2.5
E
F
D
一面镜子竖直悬挂在墙上,人眼位置如图所示,有三个物体放在镜子面前,人眼能从镜子中看见哪个物体?
C1
B1
A1
B
O
A
C
M
N
●
探索创新题
一.要点:
1.画轴对称图形是因为已知图形是整个图形的一半。
2.因为整个图形是轴对称图形,所以要作的那一半与已知图形是轴对称关系.
3.画轴对称图形的基础:作已知图形特殊点的对称点。
4.思路:把整个图形转化为多条线段,再将每条线段转化为两个端点。
二.画已知图形关于直线的轴对称图形的方法
(1)先标出特殊点
(2)逐个画出特殊点的对称点
(3)连结这些对称点
三.注意:
(1)图形用实线,其他的线可以用虚线.
(2)作垂直时要画准,等倍延长垂线段要画对.
(3)要找准各对称点.
课
堂
小
结
作
业
1.
如图是由三个小正方形组成的图形,若在图中补画一个小正方形,使它成为轴对称图形,有几种画法?然后画出图形。
2.如图所示,钱塘江的一侧有A,B两个村庄现要在江边建造一个水厂C,把水送到这两个村庄,(1)要使供水管到两村庄的距离相等,水厂C应建在何处.(2)要使供水管路线最短,水厂C应建在何处,这样可以节省成本.
.A
.B
3.已知△ABC与直线l。画出△ABC关于直线l的对称图形.
谢
谢
