人教版数学九年级上册:24.1.1圆-课件(共29张ppt)
文档属性
| 名称 | 人教版数学九年级上册:24.1.1圆-课件(共29张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 11:58:15 | ||
图片预览






文档简介
(共29张PPT)
24.1
圆的有关性质
24.1.1
圆
第二十四章
圆
学习目标:
1.通过观察实验操作,感受圆的定义,结合图形认
识弧,半圆,弦,直径,等圆,等弧,优弧,劣
弧等有关概念;
2.在具体情景中,通过探究、交流、反思等活动获
得圆的有关定义,体验探求规律的思想方法.
3.
通过对圆的认识,体验圆与日常生活密切相关。
学习重点:
圆的有关概念.
学习目标:
古希腊数学家毕达哥拉斯认为:
一切立体图形中最美的是球;
一切平面图形中最美的是圆。
观察:
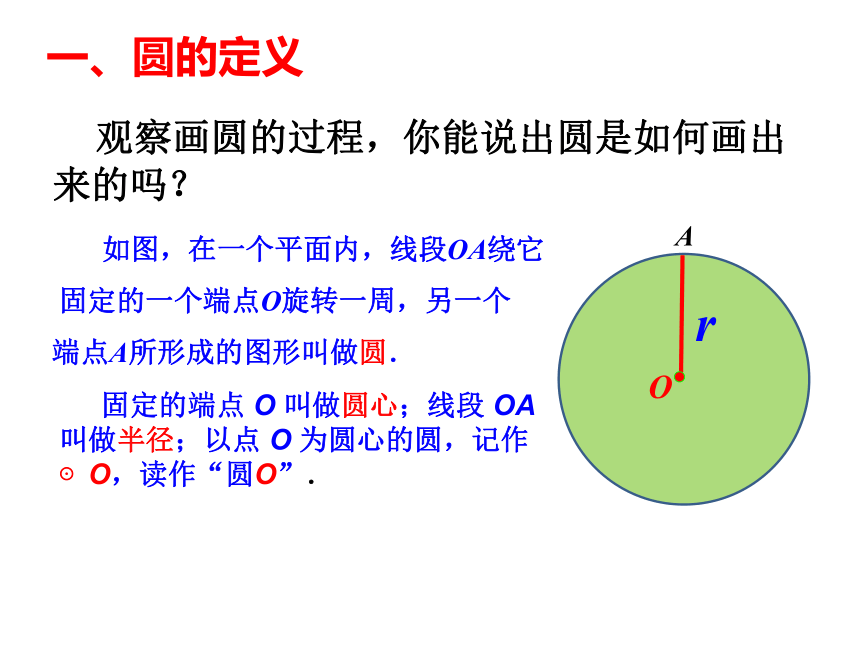
如图,在一个平面内,线段OA绕它
固定的一个端点O旋转一周,另一个
端点A所形成的图形叫做圆.
r
O
A
一、圆的定义
观察画圆的过程,你能说出圆是如何画出来的吗?
固定的端点
O
叫做圆心;线段
OA
叫做半径;以点
O
为圆心的圆,记作⊙O,读作“圆O”.
动手画一画:
(1)
以点O为圆心画圆,能画多少个?
(2)以2cm为半径画圆,能画多少个?
(3)以点O为圆心,以2cm为半径圆心画圆,能
画多少个?
同心圆
等圆
圆心相同,半径不同
半径相同,圆心不同
O
等圆
中有哪些相等的量?
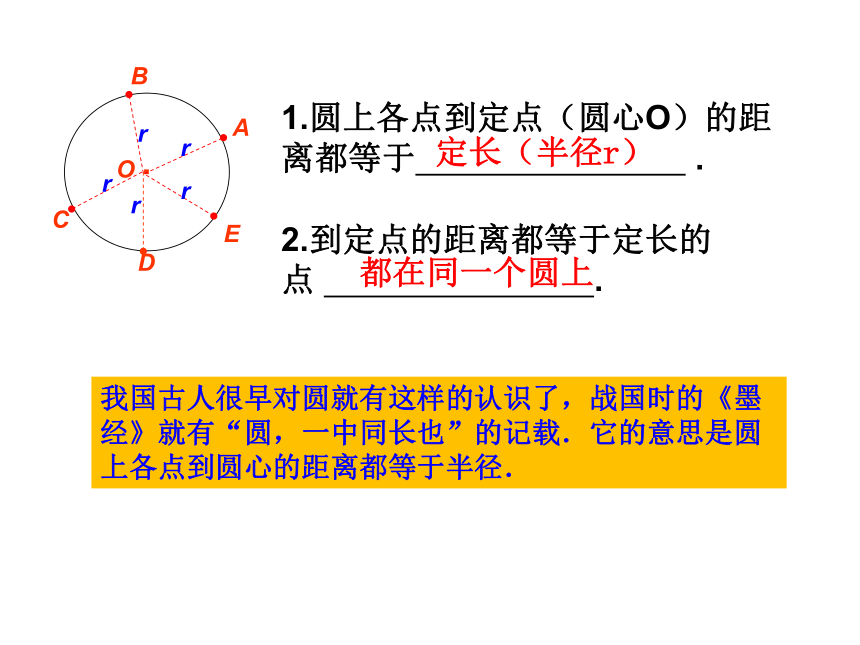
2.到定点的距离都等于定长的点
.
1.圆上各点到定点(圆心O)的距离都等于
.
O
·
A
B
C
D
E
r
r
r
r
r
我国古人很早对圆就有这样的认识了,战国时的《墨经》就有“圆,一中同长也”的记载.它的意思是圆上各点到圆心的距离都等于半径.
定长(半径r)
都在同一个圆上
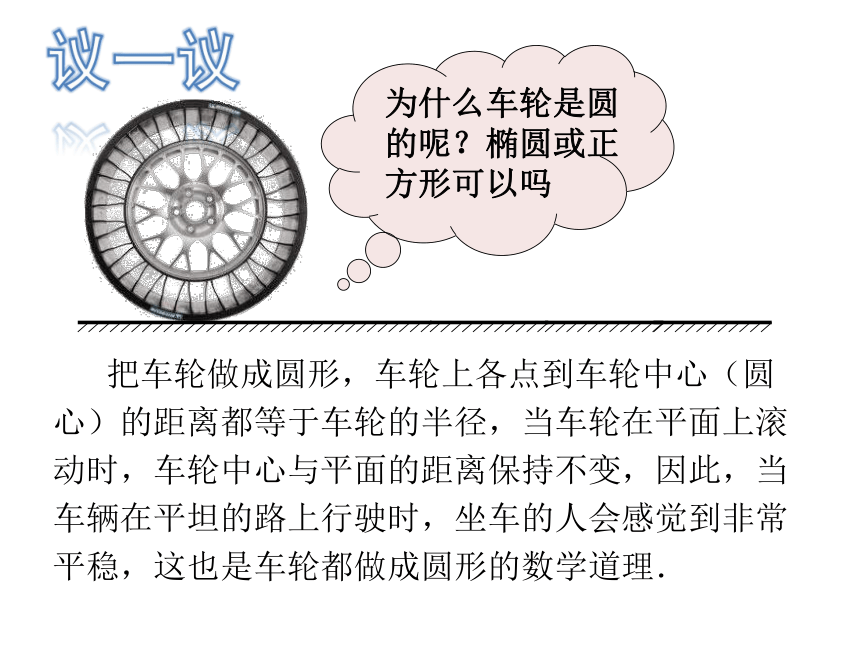
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感觉到非常平稳,这也是车轮都做成圆形的数学道理.
为什么车轮是圆的呢?椭圆或正方形可以吗
议一议
例1:
已知矩形ABCD的对角线AC,
BD相交于点O.
求证:A,
B,
C,
D四个点在以点O为圆心的
在同一个圆上。
A
B
C
D
O
·
C
O
A
B
连接圆上任意两点的线段(如图AC)叫做弦。
三、与圆有关的概念
弦
经过圆心的弦叫做直径,如图中的
AB.
●
O
B
C
A
如图,弦有
AB、
BC、
AC
●
O
B
A
●
O
D
C
·
·
C
O
A
弧
O
A
B
圆上任意两点间的部分叫做圆弧,简称弧.
D
弧
优弧:大于半圆的弧
半圆
劣弧:小于半圆的弧。
·
O
思考:你知道什么是等弧吗?
B
C
A
D
=
=
在同圆中
·
O
·
B
A
O
C
D
=
=
等弧:在同圆或等圆中,能够互相重合的弧.
在等圆中
·
O
C
D
B
A
O
·
直径d=4
直径d=8
四、圆的对称性
圆既是轴对称图形,又是中心对称图形。
·
O
1.思考:
①“直径是弦,弦是直径”这种说法对吗
?直径
是圆中最长的弦吗?
②“半圆是弧,弧是半圆”这种说法对吗?
③
面积相等的两个圆是等圆吗?周长
相等的两个圆呢?
五、有效训练,及时反馈
2.判断下列说法的正误:
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)半圆是最长的弧;
(5)圆心相同,半径相等的两个圆是同心圆;
(6)半径相等的两个半圆是等弧.
√
╳
╳
╳
╳
√
今天的学习,你有那些收获?我们来自我检测一下。
归纳小结
A
等边三角形
达标检测
5
4.
5.
生活就像一个圆,圆心是目标,圆弧是行动轨迹,只有围绕着圆心,不停地努力,才能给我们的人生交上一份圆满答案.
1.求证:直角三角形的三个顶点在同一
个圆上.
O
A
B
C
2.
已线段BC为斜边的直角三角形有多少个?它们的直角顶点是否在同一个圆上。若在,请证明;如不在,请说明理由.
C
B
A
1.
3.
24.1
圆的有关性质
24.1.1
圆
第二十四章
圆
学习目标:
1.通过观察实验操作,感受圆的定义,结合图形认
识弧,半圆,弦,直径,等圆,等弧,优弧,劣
弧等有关概念;
2.在具体情景中,通过探究、交流、反思等活动获
得圆的有关定义,体验探求规律的思想方法.
3.
通过对圆的认识,体验圆与日常生活密切相关。
学习重点:
圆的有关概念.
学习目标:
古希腊数学家毕达哥拉斯认为:
一切立体图形中最美的是球;
一切平面图形中最美的是圆。
观察:
如图,在一个平面内,线段OA绕它
固定的一个端点O旋转一周,另一个
端点A所形成的图形叫做圆.
r
O
A
一、圆的定义
观察画圆的过程,你能说出圆是如何画出来的吗?
固定的端点
O
叫做圆心;线段
OA
叫做半径;以点
O
为圆心的圆,记作⊙O,读作“圆O”.
动手画一画:
(1)
以点O为圆心画圆,能画多少个?
(2)以2cm为半径画圆,能画多少个?
(3)以点O为圆心,以2cm为半径圆心画圆,能
画多少个?
同心圆
等圆
圆心相同,半径不同
半径相同,圆心不同
O
等圆
中有哪些相等的量?
2.到定点的距离都等于定长的点
.
1.圆上各点到定点(圆心O)的距离都等于
.
O
·
A
B
C
D
E
r
r
r
r
r
我国古人很早对圆就有这样的认识了,战国时的《墨经》就有“圆,一中同长也”的记载.它的意思是圆上各点到圆心的距离都等于半径.
定长(半径r)
都在同一个圆上
把车轮做成圆形,车轮上各点到车轮中心(圆心)的距离都等于车轮的半径,当车轮在平面上滚动时,车轮中心与平面的距离保持不变,因此,当车辆在平坦的路上行驶时,坐车的人会感觉到非常平稳,这也是车轮都做成圆形的数学道理.
为什么车轮是圆的呢?椭圆或正方形可以吗
议一议
例1:
已知矩形ABCD的对角线AC,
BD相交于点O.
求证:A,
B,
C,
D四个点在以点O为圆心的
在同一个圆上。
A
B
C
D
O
·
C
O
A
B
连接圆上任意两点的线段(如图AC)叫做弦。
三、与圆有关的概念
弦
经过圆心的弦叫做直径,如图中的
AB.
●
O
B
C
A
如图,弦有
AB、
BC、
AC
●
O
B
A
●
O
D
C
·
·
C
O
A
弧
O
A
B
圆上任意两点间的部分叫做圆弧,简称弧.
D
弧
优弧:大于半圆的弧
半圆
劣弧:小于半圆的弧。
·
O
思考:你知道什么是等弧吗?
B
C
A
D
=
=
在同圆中
·
O
·
B
A
O
C
D
=
=
等弧:在同圆或等圆中,能够互相重合的弧.
在等圆中
·
O
C
D
B
A
O
·
直径d=4
直径d=8
四、圆的对称性
圆既是轴对称图形,又是中心对称图形。
·
O
1.思考:
①“直径是弦,弦是直径”这种说法对吗
?直径
是圆中最长的弦吗?
②“半圆是弧,弧是半圆”这种说法对吗?
③
面积相等的两个圆是等圆吗?周长
相等的两个圆呢?
五、有效训练,及时反馈
2.判断下列说法的正误:
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)半圆是最长的弧;
(5)圆心相同,半径相等的两个圆是同心圆;
(6)半径相等的两个半圆是等弧.
√
╳
╳
╳
╳
√
今天的学习,你有那些收获?我们来自我检测一下。
归纳小结
A
等边三角形
达标检测
5
4.
5.
生活就像一个圆,圆心是目标,圆弧是行动轨迹,只有围绕着圆心,不停地努力,才能给我们的人生交上一份圆满答案.
1.求证:直角三角形的三个顶点在同一
个圆上.
O
A
B
C
2.
已线段BC为斜边的直角三角形有多少个?它们的直角顶点是否在同一个圆上。若在,请证明;如不在,请说明理由.
C
B
A
1.
3.
同课章节目录
