人教版数学九年级上册24.1.4圆周角的概念和圆周角的定理课件(第一课时 18张)
文档属性
| 名称 | 人教版数学九年级上册24.1.4圆周角的概念和圆周角的定理课件(第一课时 18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 12:27:36 | ||
图片预览





文档简介
(共18张PPT)
新人教版九年级上册数学
24.1.4圆周角(第1课时)
问题:请同学们想一想,球员射中球门的难易与什么有关?
总结:如图所示,球员射中球门的难易与他所在的位置B对球门AC的张角(∠ABC)大小有关。
把实际图形画成图1,请同学们观察图中的∠ABC有哪些特征?
A
C
B
特征:
①
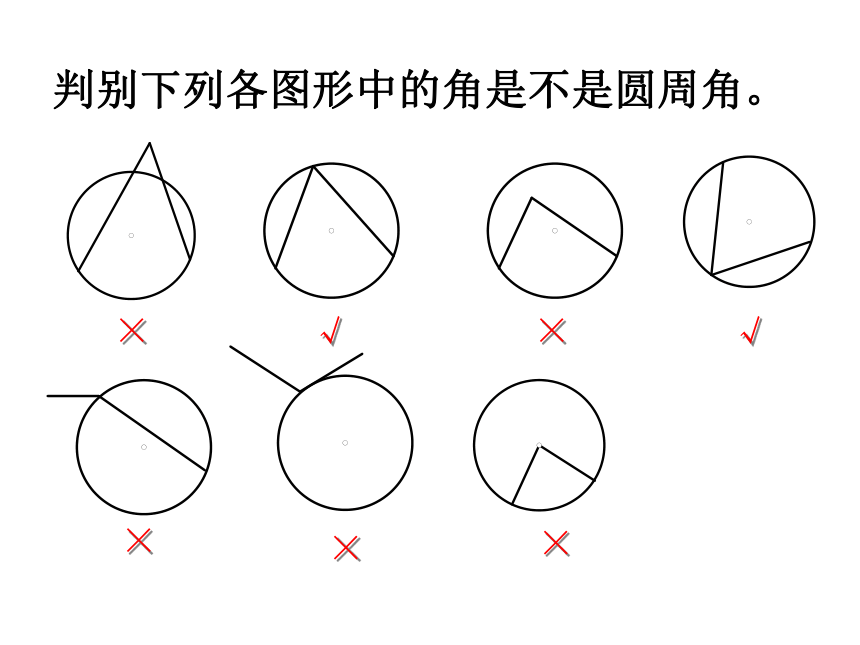
角的顶点在圆上.
②
角的两边都和圆相交(即两边是圆的两条弦)
圆周角定义:
顶点在圆上,并且两边都和圆相交的角叫圆周角.
判别下列各图形中的角是不是圆周角。
√
×
×
×
×
×
√
我们知道,在同圆或等圆中,相等的弧所对的圆心角相等,那么在同圆或等圆中,相等的弧所对的圆周角有什么关系?
要学习圆周角的关系,我们先研究:
圆心角与圆周角的关系
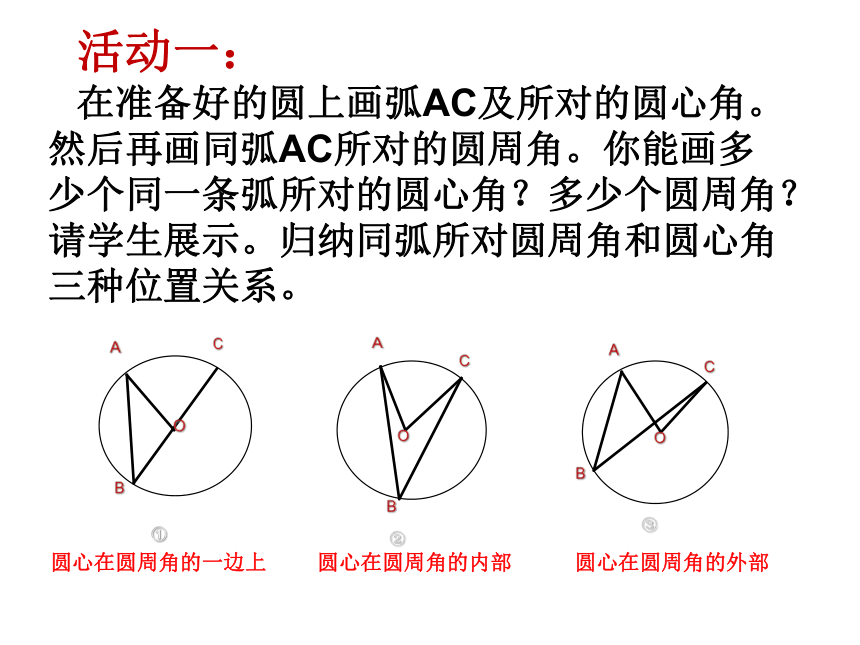
活动一:
在准备好的圆上画弧AC及所对的圆心角。然后再画同弧AC所对的圆周角。你能画多少个同一条弧所对的圆心角?多少个圆周角?请学生展示。归纳同弧所对圆周角和圆心角三种位置关系。
B
A
O
C
①
A
B
C
O
②
B
A
C
O
③
圆心在圆周角的一边上
圆心在圆周角的内部
圆心在圆周角的外部
自己动手量一量同一条弧所对的圆心角和圆周角分别是多少度?猜想它们有什么关系?
活动二:猜想、测量
A
B
C
●O
●O
A
B
C
A
B
C
●O
一条弧所对的圆周角等于它所对的圆心角的一半
圆周角和圆心角的关系
分类讨论1:当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系。(重点掌握)
●O
A
B
C
解:∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
∵OA=OB,
∴∠A=∠B.
∴∠AOC=2∠B.
即
∠ABC
=
∠AOC.
理解并掌握这个模型.
分类讨论2:当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
提示:能否转化为1的情况?
●O
A
B
C
D
过点B作直径BD.由1可得:
∠ABD
=
∠AOD,∠CBD
=
∠COD,
∴
∠ABC
=
∠AOC.
提示:能否也转化为1的情况?
过点B作直径BD.由1可得:
∴
∠ABC
=
∠AOC.
一条弧所对的圆周角等于它所对的圆心角的一半.
∠ABD
=
∠AOD,∠CBD
=
∠COD,
分类讨论3:当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
D
●O
A
B
C
活动三:学以致用
1.
如图1,在圆O中,
∠BOC=50°,则∠BAC
=
;
2.变式1:如图2,已知∠BCD=120°,则∠AOB=
;
3.变式2:如图3,已知圆心角∠AOB=100°,则
∠ACB
=
,∠ADB
= .
O
A
B
C
(图1)
A
O
.
120°
(图2)
(图3)
O
A
B
25°
120°
50°
130°
D
C
C
D
例题讲解:
例1.如图:OA、OB、OC都是⊙
O的半径
∠AOB=2∠BOC.
∠ACB=40°,求∠BAC的度数.
⌒
分析:AB所对圆周角是∠ACB,
圆心角是∠AOB.则∠ACB=
∠AOB.
BC所对圆周角是∠
BAC
,
圆心角是∠BOC,
则∠
BAC=
∠BOC
⌒
A
O
B
C
例1.如图:OA、OB、OC都是⊙
O的半径
∠AOB=2∠BOC.
∠ACB=40°,求∠BAC的度数.
A
O
B
C
证明:
规律:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理
∵
∠ACB=
∠AOB=40
°
∴
∠BOC=40
°
∴
∠BAC=20°
∴
∠AOB=
80
°
∵
∠AOB=2∠BOC
∵
∠BAC=
∠BOC
1、(宁德中考)如图,在⊙O中,∠ACB=34°,则∠AOB的度数是(
).
A.17°
B.34°
C.56°
D.68°
A
O
C
B
2、(三明中考)如图,A、B、C是⊙O上的三点,∠AOC=100°,则∠ABC的度数为(
)
A.30°
B.45°
C.50°
D.60°
活动四:走进中考
D
C
4、(莆田中考)如图,△ABC内接于⊙O,∠A=50°,则∠OBC的度数为( )
A.40°
B.50°
C.80°
D.100°
3、(龙岩中考)如图,A、B、P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为( )
A.
B.
C.
D.
B
A
课堂小结:
1、本节课你都学到了什么?
2、在思想方法上有哪些收获与体验?
今天的作业:
第89~90页习题第5、14题;
作业
知识小结:
祝你进步!
今天我们学习了圆周角及定理的证明,可以把复杂的图形向简单的图形转化,这样复杂的问题就容易解决了.
今天,我们通过“画一画”“量一量””猜一猜“”想一想“学会了有关圆周角定理,在今后的有关计算中很有用.
希望同学们每一堂课都有收获,取得更大进步.
下课了!
结束寄语
再
见
新人教版九年级上册数学
24.1.4圆周角(第1课时)
问题:请同学们想一想,球员射中球门的难易与什么有关?
总结:如图所示,球员射中球门的难易与他所在的位置B对球门AC的张角(∠ABC)大小有关。
把实际图形画成图1,请同学们观察图中的∠ABC有哪些特征?
A
C
B
特征:
①
角的顶点在圆上.
②
角的两边都和圆相交(即两边是圆的两条弦)
圆周角定义:
顶点在圆上,并且两边都和圆相交的角叫圆周角.
判别下列各图形中的角是不是圆周角。
√
×
×
×
×
×
√
我们知道,在同圆或等圆中,相等的弧所对的圆心角相等,那么在同圆或等圆中,相等的弧所对的圆周角有什么关系?
要学习圆周角的关系,我们先研究:
圆心角与圆周角的关系
活动一:
在准备好的圆上画弧AC及所对的圆心角。然后再画同弧AC所对的圆周角。你能画多少个同一条弧所对的圆心角?多少个圆周角?请学生展示。归纳同弧所对圆周角和圆心角三种位置关系。
B
A
O
C
①
A
B
C
O
②
B
A
C
O
③
圆心在圆周角的一边上
圆心在圆周角的内部
圆心在圆周角的外部
自己动手量一量同一条弧所对的圆心角和圆周角分别是多少度?猜想它们有什么关系?
活动二:猜想、测量
A
B
C
●O
●O
A
B
C
A
B
C
●O
一条弧所对的圆周角等于它所对的圆心角的一半
圆周角和圆心角的关系
分类讨论1:当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系。(重点掌握)
●O
A
B
C
解:∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
∵OA=OB,
∴∠A=∠B.
∴∠AOC=2∠B.
即
∠ABC
=
∠AOC.
理解并掌握这个模型.
分类讨论2:当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
提示:能否转化为1的情况?
●O
A
B
C
D
过点B作直径BD.由1可得:
∠ABD
=
∠AOD,∠CBD
=
∠COD,
∴
∠ABC
=
∠AOC.
提示:能否也转化为1的情况?
过点B作直径BD.由1可得:
∴
∠ABC
=
∠AOC.
一条弧所对的圆周角等于它所对的圆心角的一半.
∠ABD
=
∠AOD,∠CBD
=
∠COD,
分类讨论3:当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样?
D
●O
A
B
C
活动三:学以致用
1.
如图1,在圆O中,
∠BOC=50°,则∠BAC
=
;
2.变式1:如图2,已知∠BCD=120°,则∠AOB=
;
3.变式2:如图3,已知圆心角∠AOB=100°,则
∠ACB
=
,∠ADB
= .
O
A
B
C
(图1)
A
O
.
120°
(图2)
(图3)
O
A
B
25°
120°
50°
130°
D
C
C
D
例题讲解:
例1.如图:OA、OB、OC都是⊙
O的半径
∠AOB=2∠BOC.
∠ACB=40°,求∠BAC的度数.
⌒
分析:AB所对圆周角是∠ACB,
圆心角是∠AOB.则∠ACB=
∠AOB.
BC所对圆周角是∠
BAC
,
圆心角是∠BOC,
则∠
BAC=
∠BOC
⌒
A
O
B
C
例1.如图:OA、OB、OC都是⊙
O的半径
∠AOB=2∠BOC.
∠ACB=40°,求∠BAC的度数.
A
O
B
C
证明:
规律:解决圆周角和圆心角的计算和证明问题,要准确找出同弧所对的圆周角和圆心角,然后再灵活运用圆周角定理
∵
∠ACB=
∠AOB=40
°
∴
∠BOC=40
°
∴
∠BAC=20°
∴
∠AOB=
80
°
∵
∠AOB=2∠BOC
∵
∠BAC=
∠BOC
1、(宁德中考)如图,在⊙O中,∠ACB=34°,则∠AOB的度数是(
).
A.17°
B.34°
C.56°
D.68°
A
O
C
B
2、(三明中考)如图,A、B、C是⊙O上的三点,∠AOC=100°,则∠ABC的度数为(
)
A.30°
B.45°
C.50°
D.60°
活动四:走进中考
D
C
4、(莆田中考)如图,△ABC内接于⊙O,∠A=50°,则∠OBC的度数为( )
A.40°
B.50°
C.80°
D.100°
3、(龙岩中考)如图,A、B、P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为( )
A.
B.
C.
D.
B
A
课堂小结:
1、本节课你都学到了什么?
2、在思想方法上有哪些收获与体验?
今天的作业:
第89~90页习题第5、14题;
作业
知识小结:
祝你进步!
今天我们学习了圆周角及定理的证明,可以把复杂的图形向简单的图形转化,这样复杂的问题就容易解决了.
今天,我们通过“画一画”“量一量””猜一猜“”想一想“学会了有关圆周角定理,在今后的有关计算中很有用.
希望同学们每一堂课都有收获,取得更大进步.
下课了!
结束寄语
再
见
同课章节目录
