湘教版(2012)初中数学七年级上册 3.2 等式的性质 课件(39张)
文档属性
| 名称 | 湘教版(2012)初中数学七年级上册 3.2 等式的性质 课件(39张) |

|
|
| 格式 | zip | ||
| 文件大小 | 797.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 00:00:00 | ||
图片预览











文档简介
(共39张PPT)
3.2
等式的性质
学习目标:
1.
了解等式的概念和等式的两条性质并能运用这两条性质解简单的一元一次方程.
2.
经历等式的两条性质的探究过程,培养观察、归纳的能力.
3.
在运用等式的性质把简单的一元一次方程化成x=a的形式的过程中,渗透数学思想.
学习重点:
了解等式的两条性质并能运用它们解简单的一元一次方程.
学习难点:
运用等式性质把简单的一元一次方程化成x=a的形式。
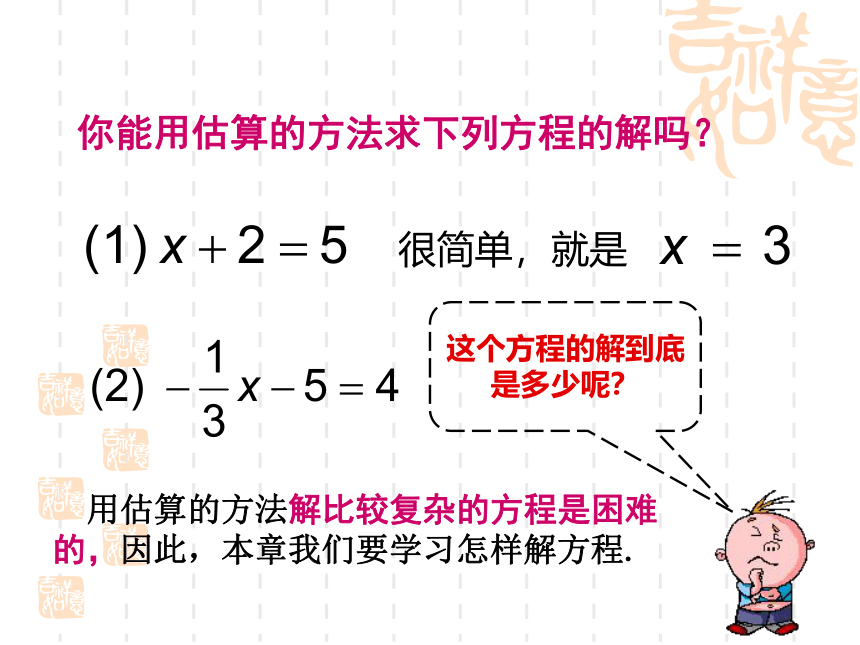
你能用估算的方法求下列方程的解吗?
很简单,就是
这个方程的解到底是多少呢?
用估算的方法解比较复杂的方程是困难的,因此,本章我们要学习怎样解方程.
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
等式性质1:
,那么
如果
等式两边加(或减)同一个数(或式子),结果
仍相等。
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
等式两边乘同一个数,或除以同一个不为0的数,
结果仍相等。
,那么
如果
,那么
如果
等式性质2:
如果
,那么
(
)
如果
,那么
(
)
如果
,那么
(
)
如果
,那么
(
)
如果
,那么
(
)
如果
,
那么
(
)
√
×
×
×
√
√
判断对错(根据等
式的哪一条性质?)
趁热打铁
例1
填空,并说明理由
(1)如果a+2
=
b+7,那么a=
;
(2)如果3x
=
9y,那么
x=
;
(3)如果
,那么3a=
.
b
+
5
3y
2b
学以致用
例2
判断下列等式变形是
否正确,并改正.
(1)如果a-3=2b-5,那么a
=2b
-8;
(2)如果
,那么
10x
-5=16x
-8.
解
错误.
由等式性质1可知,等式两边都加上3,
得
a-3+3=2b-5+3
即
a
=
2b
-
2
.
解
正确
由等式性质2可知,等式两边都乘20,得
×20
=
×20
即
5(2x-1)
=
4(4x-2)
去括号,得
10x-5=16x-8.
学以致用
例3
利用等式的性质解下列方程
解:两边减7,得
于是
解:两边除以-5,得
于是
学以
例4
利用等式的性质解下列方程
解:两边加5,得
化简,得
两边同乘-3,得
检验:
将
代入方程
,得:
左边
右边
所以
是方程
的解。
学以
利用等式的性质解
下列方程并写出检验
解:两边加5,得
于是
方程
检验:把
代入
左边
右边
,得:
所以
是方程的解
解:两边除以0.3,得
于是
方程
检验:把
代入
左边
右边
,得:
所以
是方程的解
小试牛刀
解:两边减2,得:
化简得:
两边乘-4,得:
方程
检验:
左边
右边
,得:
所以
是方程的解
把
代入
小试牛刀
利用等式的性质解
下列方程并写出检验
解:两边减4,得:
化简得:
两边除以5,得:
方程
检验:
左边
右边
,得:
所以
是方程的解
把
代入
小试牛刀
利用等式的性质解
下列方程并写出检验
1、等式的性质有几条?用字母怎样表示?
2、解方程最终必须将方程化作什么形式?
课堂小结
用等式的性质解下列方程并检验:
(1)x-5=6;
(2)0.3x=45;
(3)5x+4=0;
(4)
.
解:
(1)两边加5,得
x-5+5=6+5.
于是
x=11.
检验:
当x=11时,左边=11-5=6=右边,
所以x=11是原方程的解.
课堂作业
3.2
等式的性质
学习目标:
1.
了解等式的概念和等式的两条性质并能运用这两条性质解简单的一元一次方程.
2.
经历等式的两条性质的探究过程,培养观察、归纳的能力.
3.
在运用等式的性质把简单的一元一次方程化成x=a的形式的过程中,渗透数学思想.
学习重点:
了解等式的两条性质并能运用它们解简单的一元一次方程.
学习难点:
运用等式性质把简单的一元一次方程化成x=a的形式。
你能用估算的方法求下列方程的解吗?
很简单,就是
这个方程的解到底是多少呢?
用估算的方法解比较复杂的方程是困难的,因此,本章我们要学习怎样解方程.
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
探究等式性质1
等式性质1:
,那么
如果
等式两边加(或减)同一个数(或式子),结果
仍相等。
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
探究等式性质2
等式两边乘同一个数,或除以同一个不为0的数,
结果仍相等。
,那么
如果
,那么
如果
等式性质2:
如果
,那么
(
)
如果
,那么
(
)
如果
,那么
(
)
如果
,那么
(
)
如果
,那么
(
)
如果
,
那么
(
)
√
×
×
×
√
√
判断对错(根据等
式的哪一条性质?)
趁热打铁
例1
填空,并说明理由
(1)如果a+2
=
b+7,那么a=
;
(2)如果3x
=
9y,那么
x=
;
(3)如果
,那么3a=
.
b
+
5
3y
2b
学以致用
例2
判断下列等式变形是
否正确,并改正.
(1)如果a-3=2b-5,那么a
=2b
-8;
(2)如果
,那么
10x
-5=16x
-8.
解
错误.
由等式性质1可知,等式两边都加上3,
得
a-3+3=2b-5+3
即
a
=
2b
-
2
.
解
正确
由等式性质2可知,等式两边都乘20,得
×20
=
×20
即
5(2x-1)
=
4(4x-2)
去括号,得
10x-5=16x-8.
学以致用
例3
利用等式的性质解下列方程
解:两边减7,得
于是
解:两边除以-5,得
于是
学以
例4
利用等式的性质解下列方程
解:两边加5,得
化简,得
两边同乘-3,得
检验:
将
代入方程
,得:
左边
右边
所以
是方程
的解。
学以
利用等式的性质解
下列方程并写出检验
解:两边加5,得
于是
方程
检验:把
代入
左边
右边
,得:
所以
是方程的解
解:两边除以0.3,得
于是
方程
检验:把
代入
左边
右边
,得:
所以
是方程的解
小试牛刀
解:两边减2,得:
化简得:
两边乘-4,得:
方程
检验:
左边
右边
,得:
所以
是方程的解
把
代入
小试牛刀
利用等式的性质解
下列方程并写出检验
解:两边减4,得:
化简得:
两边除以5,得:
方程
检验:
左边
右边
,得:
所以
是方程的解
把
代入
小试牛刀
利用等式的性质解
下列方程并写出检验
1、等式的性质有几条?用字母怎样表示?
2、解方程最终必须将方程化作什么形式?
课堂小结
用等式的性质解下列方程并检验:
(1)x-5=6;
(2)0.3x=45;
(3)5x+4=0;
(4)
.
解:
(1)两边加5,得
x-5+5=6+5.
于是
x=11.
检验:
当x=11时,左边=11-5=6=右边,
所以x=11是原方程的解.
课堂作业
同课章节目录
