湘教版八年级数学上册 2.5.2全等三角形ASA 课件(19张)
文档属性
| 名称 | 湘教版八年级数学上册 2.5.2全等三角形ASA 课件(19张) |  | |
| 格式 | zip | ||
| 文件大小 | 170.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 13:55:05 | ||
图片预览


文档简介
(共19张PPT)
2.5.2全等三角形的判定
(ASA)
⌒
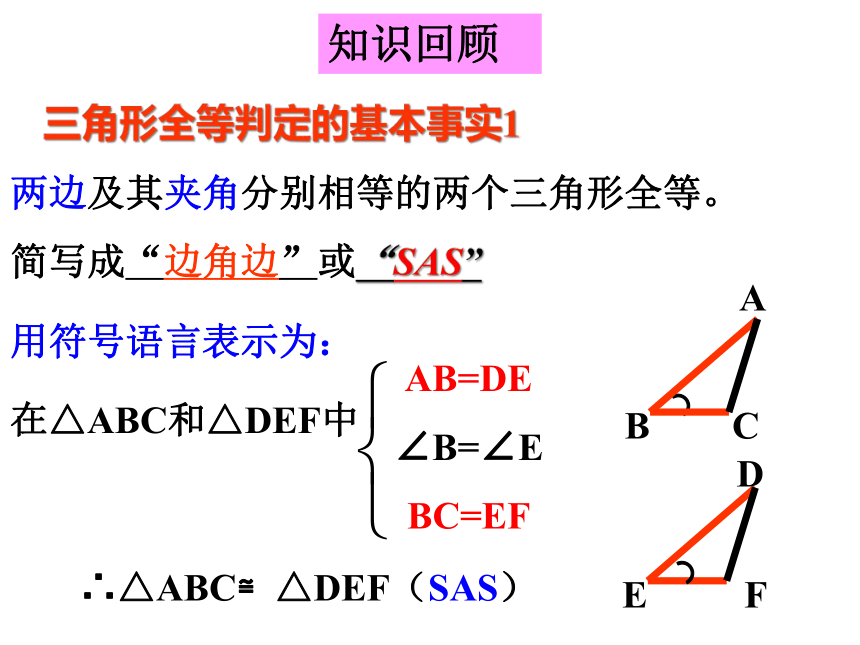
三角形全等判定的基本事实1
用符号语言表示为:
在△ABC和△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
A
B
C
D
E
F
两边及其夹角分别相等的两个三角形全等。
简写成“边角边”或“SAS”
知识回顾
⌒
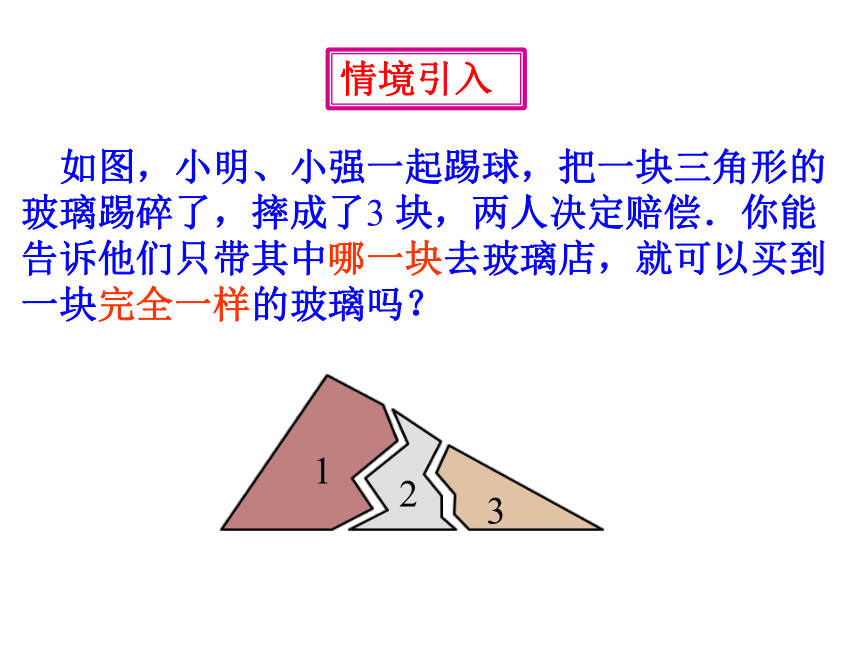
情境引入
如图,小明、小强一起踢球,把一块三角形的玻璃踢碎了,摔成了3
块,两人决定赔偿.你能告诉他们只带其中哪一块去玻璃店,就可以买到一块完全一样的玻璃吗?
3
2
1
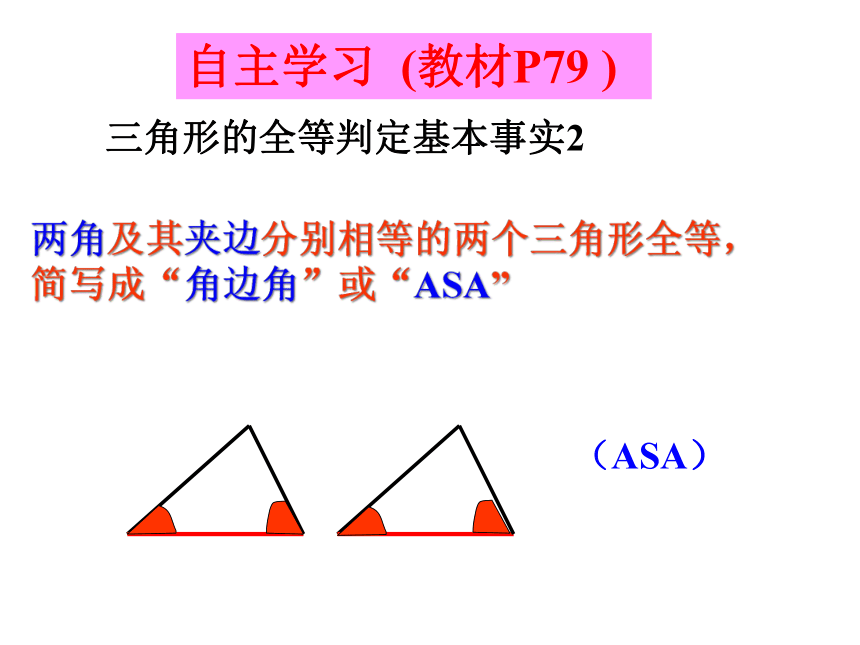
自主学习
(教材P79
)
三角形的全等判定基本事实2
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”
(ASA)
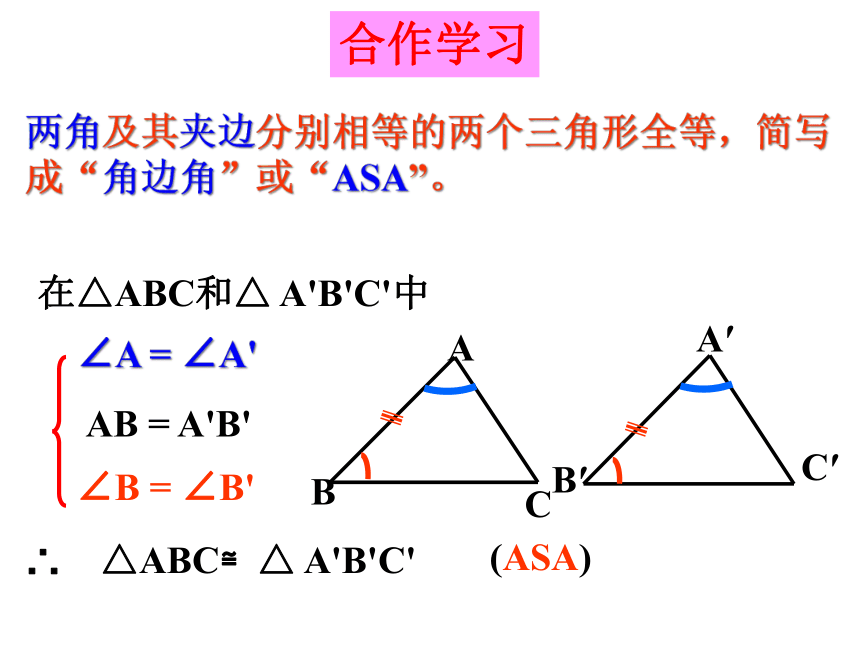
在△ABC和△
A'B'C'中
∠A
=
∠A'
AB
=
A'B'
∠B
=
∠B'
∴
△ABC≌△
A'B'C'
(ASA)
A
C
B
A′
C′
B′
合作学习
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”。
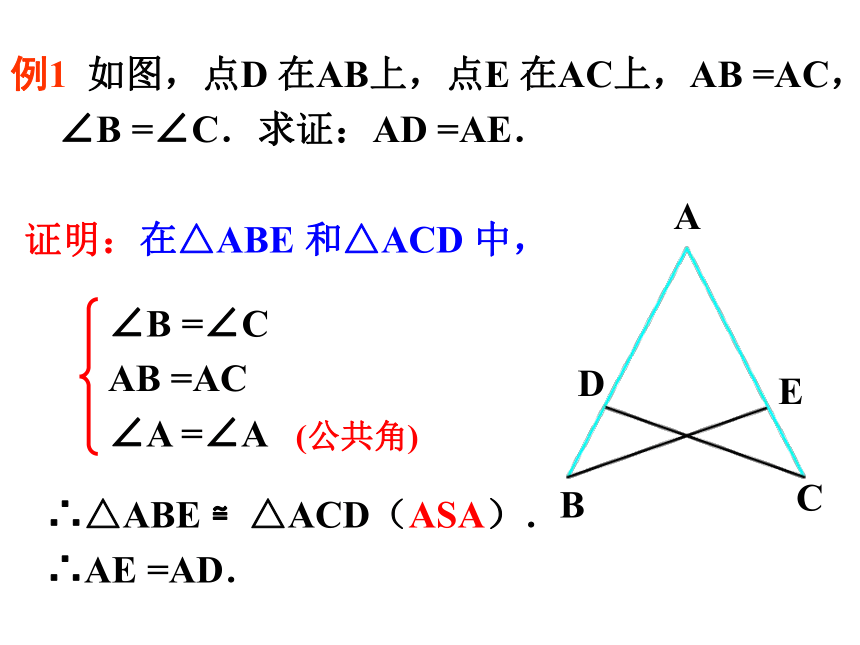
证明:在△ABE
和△ACD
中,
∴△ABE
≌△ACD(ASA).
∴AE
=AD.
∠B
=∠C
AB
=AC
∠A
=∠A
例1
如图,点D
在AB上,点E
在AC上,AB
=AC,
∠B
=∠C.求证:AD
=AE.
A
B
C
D
E
(公共角)
例2
如图,已知点E,C在线段BF上,BE=CF,
AB∥DE,∠ACB=∠F.
求证:△ABC≌△DEF.
证明:∵BE=CF
∴BE+EC=CF+EC,
即BC=EF
又∵AB∥DE
,
∴∠B=∠DEF
在△ABC
和△DEF
中,
∠B
=∠DEF,
BC=EF,
∠ACB=∠F,
∴△ABC≌△DEF(ASA).
1、
已知:如图,AB=AE,∠1=∠2,∠B=∠E,
求证:BC=ED.
练习
2、
如图,为测量河宽AB,小军从河岸的A点沿着与AB垂直的方向走到C点,并在AC的中点E处立一根标杆,然后从C点沿着和AC垂直的方向走到D点,使点D,E,B恰好在一条直线上.于是小军说:“CD的长就是河的宽度.”你能说出这个道理吗?
B
A
E
C
D
证明:
在△AEB和△CED中,
∠A=∠C=
90°,
AE=CE,
∠AEB
=∠CED
,
∴
△AEB
≌
△CED(ASA).
∴
AB=CD
因此,CD的长就是河的宽度.
应用“ASA”
判定方法,解决实际问题
如图,小明、小强一起踢球,把一块三角形的玻璃踢碎了,摔成了3
块,两人决定赔偿.你能告诉他们只带其中哪一块去玻璃店,就可以买到一块完全一样的玻璃吗?
3
2
1
已知,如图:∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF,若以“ASA”为依据,还要添加的条件为_________.
课堂练习
能确定△ABC
≌△DEF
的条件是(
)
A.AB=DE,BC=EF,∠A=∠E
B.AB=DE,BC=EF,∠C=∠E
C.∠A=∠E,AB=EF,∠B=∠D
D.∠A=∠D,AB=DE,∠B=∠E
课堂练习
E
A
B
C
F
D
如图,点D、E、F、B在同一直线上,∠A=∠C、AE∥CF,且AE=CF,若BD=10,BF=2,
则EF=________.
如图,点A、F、E、C在同一直线上,AF=CE,
AB∥DC,
BE∥DF
.
求证:AB=CD.
已知:如图,PM=PN,∠M=∠N.
求证:AM=BN.
课堂小结
本节课学习了哪种判断两个三角形全等的方法?
如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,求线段DF的长.
拓展提升
已知,如图所示,两直线AB,CD相交于点O,AO=BO,CO=DO,直线EF过点O且分别交AC,BD于点E,F,求证:OE=OF.
拓展提升
2.5.2全等三角形的判定
(ASA)
⌒
三角形全等判定的基本事实1
用符号语言表示为:
在△ABC和△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
A
B
C
D
E
F
两边及其夹角分别相等的两个三角形全等。
简写成“边角边”或“SAS”
知识回顾
⌒
情境引入
如图,小明、小强一起踢球,把一块三角形的玻璃踢碎了,摔成了3
块,两人决定赔偿.你能告诉他们只带其中哪一块去玻璃店,就可以买到一块完全一样的玻璃吗?
3
2
1
自主学习
(教材P79
)
三角形的全等判定基本事实2
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”
(ASA)
在△ABC和△
A'B'C'中
∠A
=
∠A'
AB
=
A'B'
∠B
=
∠B'
∴
△ABC≌△
A'B'C'
(ASA)
A
C
B
A′
C′
B′
合作学习
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”。
证明:在△ABE
和△ACD
中,
∴△ABE
≌△ACD(ASA).
∴AE
=AD.
∠B
=∠C
AB
=AC
∠A
=∠A
例1
如图,点D
在AB上,点E
在AC上,AB
=AC,
∠B
=∠C.求证:AD
=AE.
A
B
C
D
E
(公共角)
例2
如图,已知点E,C在线段BF上,BE=CF,
AB∥DE,∠ACB=∠F.
求证:△ABC≌△DEF.
证明:∵BE=CF
∴BE+EC=CF+EC,
即BC=EF
又∵AB∥DE
,
∴∠B=∠DEF
在△ABC
和△DEF
中,
∠B
=∠DEF,
BC=EF,
∠ACB=∠F,
∴△ABC≌△DEF(ASA).
1、
已知:如图,AB=AE,∠1=∠2,∠B=∠E,
求证:BC=ED.
练习
2、
如图,为测量河宽AB,小军从河岸的A点沿着与AB垂直的方向走到C点,并在AC的中点E处立一根标杆,然后从C点沿着和AC垂直的方向走到D点,使点D,E,B恰好在一条直线上.于是小军说:“CD的长就是河的宽度.”你能说出这个道理吗?
B
A
E
C
D
证明:
在△AEB和△CED中,
∠A=∠C=
90°,
AE=CE,
∠AEB
=∠CED
,
∴
△AEB
≌
△CED(ASA).
∴
AB=CD
因此,CD的长就是河的宽度.
应用“ASA”
判定方法,解决实际问题
如图,小明、小强一起踢球,把一块三角形的玻璃踢碎了,摔成了3
块,两人决定赔偿.你能告诉他们只带其中哪一块去玻璃店,就可以买到一块完全一样的玻璃吗?
3
2
1
已知,如图:∠ABC=∠DEF,AB=DE,要说明△ABC≌△DEF,若以“ASA”为依据,还要添加的条件为_________.
课堂练习
能确定△ABC
≌△DEF
的条件是(
)
A.AB=DE,BC=EF,∠A=∠E
B.AB=DE,BC=EF,∠C=∠E
C.∠A=∠E,AB=EF,∠B=∠D
D.∠A=∠D,AB=DE,∠B=∠E
课堂练习
E
A
B
C
F
D
如图,点D、E、F、B在同一直线上,∠A=∠C、AE∥CF,且AE=CF,若BD=10,BF=2,
则EF=________.
如图,点A、F、E、C在同一直线上,AF=CE,
AB∥DC,
BE∥DF
.
求证:AB=CD.
已知:如图,PM=PN,∠M=∠N.
求证:AM=BN.
课堂小结
本节课学习了哪种判断两个三角形全等的方法?
如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,求线段DF的长.
拓展提升
已知,如图所示,两直线AB,CD相交于点O,AO=BO,CO=DO,直线EF过点O且分别交AC,BD于点E,F,求证:OE=OF.
拓展提升
同课章节目录
