人教版九年级上册中考数学复习24.4圆的弧长和扇形面积专题巩固与提升练习(Word版无答案)
文档属性
| 名称 | 人教版九年级上册中考数学复习24.4圆的弧长和扇形面积专题巩固与提升练习(Word版无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 766.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 09:40:19 | ||
图片预览

文档简介
中考数学复习
《圆的弧长和扇形面积》专题巩固与提升练习
常用公式:
1.弧长公式
在半径为R的圆中,
(1)360°的圆心角所对的弧长是圆的周长C=
;
(2)1°的圆心角所对的弧长是?
,即?
;
(3)n°的圆心角所对的弧长为?
,即l=?
.?
2.扇形面积公式
在半径为R的圆中,
(1)360°的圆心角所对的扇形面积是圆的面积S=
;
(2)所以圆心角是1°的扇形面积是?
;
(3)圆心角是n°的扇形面积是?
,
即S扇形=
=
=?
.(其中l为扇形弧长)?
一.选择题.
1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( C )
A.π
B.2π
C.3π
D.6π
2.圆心角为60°,弧长为2π的扇形的半径为( C )
A.3
B.6π
C.6
D.12
3.如图,线段AB经过☉O的圆心,AC,BD分别与☉O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为
( )
A.π
B.2π
C.2π
D.4π
4.一个扇形的半径为6,圆心角为120°,则该扇形的面积是( )
A.2π
B.4π
C.12π
D.24π
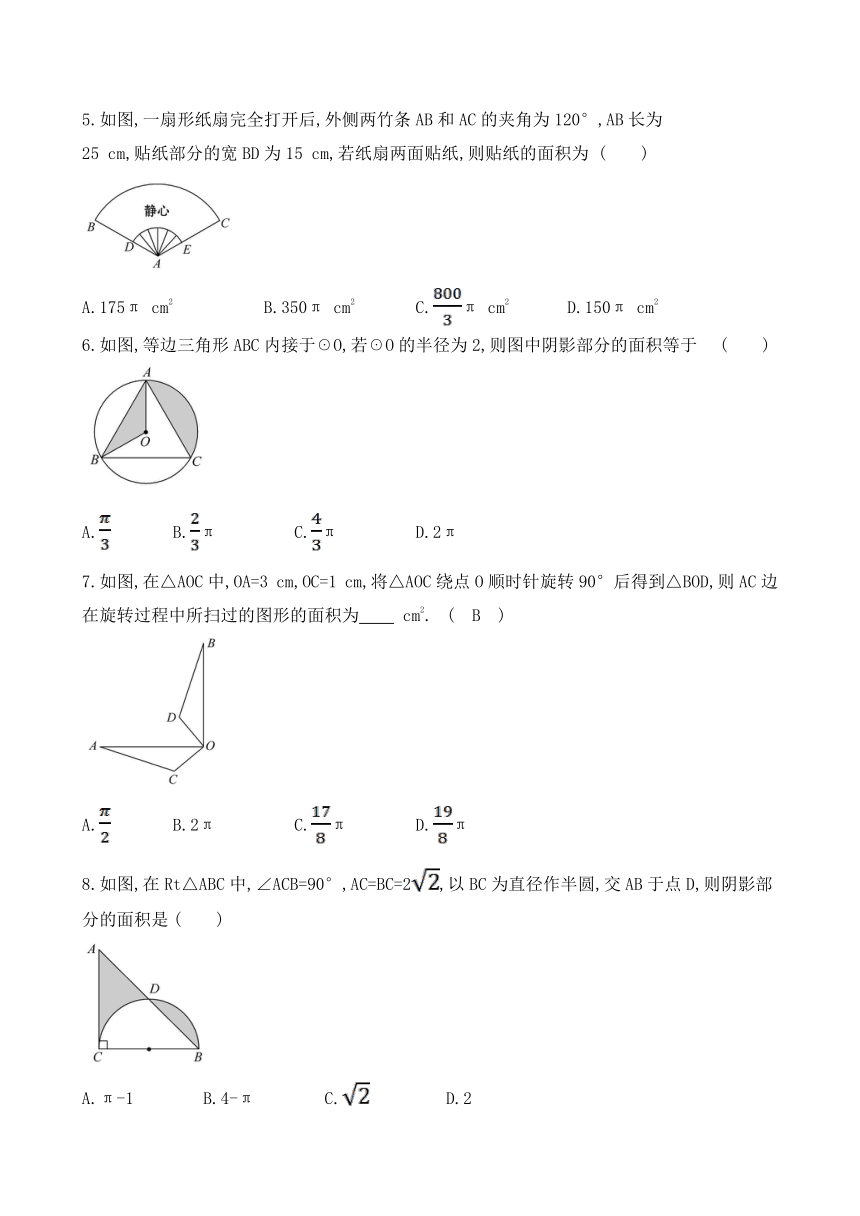
5.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为
25
cm,贴纸部分的宽BD为15
cm,若纸扇两面贴纸,则贴纸的面积为
( )
A.175π
cm2
B.350π
cm2
C.π
cm2
D.150π
cm2
6.如图,等边三角形ABC内接于☉O,若☉O的半径为2,则图中阴影部分的面积等于
( )
A.
B.π
C.π
D.2π
7.如图,在△AOC中,OA=3
cm,OC=1
cm,将△AOC绕点O顺时针旋转90°后得到△BOD,则AC边在旋转过程中所扫过的图形的面积为
cm2.
( B )?
A.
B.2π
C.π
D.π
8.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径作半圆,交AB于点D,则阴影部分的面积是
( )
A.π-1
B.4-π
C.
D.2
二.填空题.
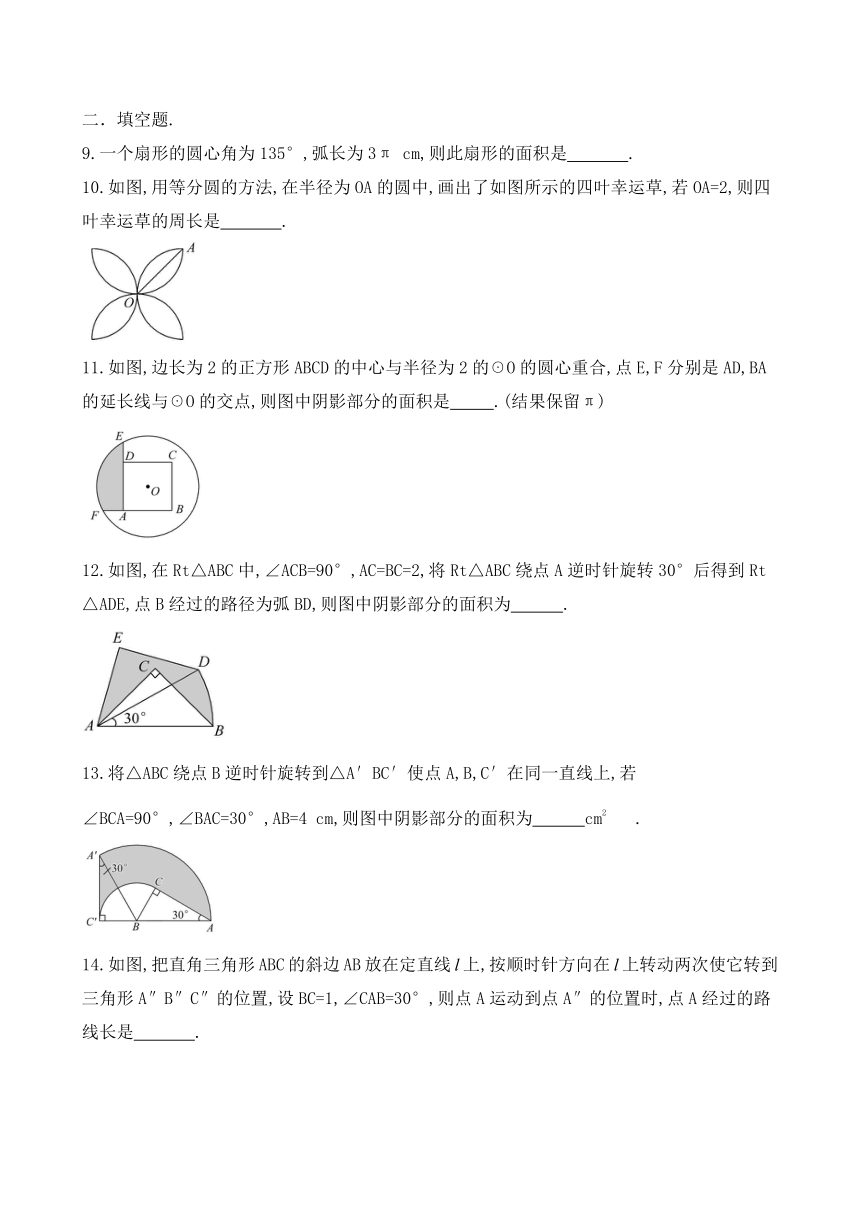
9.一个扇形的圆心角为135°,弧长为3π
cm,则此扇形的面积是
.?
10.如图,用等分圆的方法,在半径为OA的圆中,画出了如图所示的四叶幸运草,若OA=2,则四叶幸运草的周长是
.?
11.如图,边长为2的正方形ABCD的中心与半径为2的☉O的圆心重合,点E,F分别是AD,BA的延长线与☉O的交点,则图中阴影部分的面积是
.(结果保留π)?
12.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则图中阴影部分的面积为?
.?
13.将△ABC绕点B逆时针旋转到△A′BC′使点A,B,C′在同一直线上,若
∠BCA=90°,∠BAC=30°,AB=4
cm,则图中阴影部分的面积为
cm2.
14.如图,把直角三角形ABC的斜边AB放在定直线l上,按顺时针方向在l上转动两次使它转到三角形A″B″C″的位置,设BC=1,∠CAB=30°,则点A运动到点A″的位置时,点A经过的路线长是?
.?
15.如图,AB是半圆O的直径,点C,D是半圆O的三等分点,若弦CD=2,则图中阴影部分的面积为?
.
三.解答题.
16.如图,以△ABC的边BC为直径作☉O,点A在☉O上,点D在线段BC的延长线上,AD=AB,∠D=30°.
(1)求证:直线AD是☉O的切线;
(2)若直径BC=4,求图中阴影部分的面积.
17.
如图,圆锥的底面半径为6
cm,高为8
cm,求这个圆锥的侧面积和表面积.
18.
如图,有一直径是
m的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC.
(1)求AB的长;
(2)求图中阴影部分的面积;
(3)若用该扇形铁皮围成一个圆锥,求所得圆锥的底面圆半径.
19.
如图,点A、B、C在半径为8的☉O上,过点B作BD∥AC,交OA延长线于点D.连接BC,且∠BCA=∠OAC=30°.
(1)求证:BD是☉O的切线;
(2)求图中阴影部分的面积.
PAGE
《圆的弧长和扇形面积》专题巩固与提升练习
常用公式:
1.弧长公式
在半径为R的圆中,
(1)360°的圆心角所对的弧长是圆的周长C=
;
(2)1°的圆心角所对的弧长是?
,即?
;
(3)n°的圆心角所对的弧长为?
,即l=?
.?
2.扇形面积公式
在半径为R的圆中,
(1)360°的圆心角所对的扇形面积是圆的面积S=
;
(2)所以圆心角是1°的扇形面积是?
;
(3)圆心角是n°的扇形面积是?
,
即S扇形=
=
=?
.(其中l为扇形弧长)?
一.选择题.
1.若扇形的圆心角为90°,半径为6,则该扇形的弧长为( C )
A.π
B.2π
C.3π
D.6π
2.圆心角为60°,弧长为2π的扇形的半径为( C )
A.3
B.6π
C.6
D.12
3.如图,线段AB经过☉O的圆心,AC,BD分别与☉O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为
( )
A.π
B.2π
C.2π
D.4π
4.一个扇形的半径为6,圆心角为120°,则该扇形的面积是( )
A.2π
B.4π
C.12π
D.24π
5.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为
25
cm,贴纸部分的宽BD为15
cm,若纸扇两面贴纸,则贴纸的面积为
( )
A.175π
cm2
B.350π
cm2
C.π
cm2
D.150π
cm2
6.如图,等边三角形ABC内接于☉O,若☉O的半径为2,则图中阴影部分的面积等于
( )
A.
B.π
C.π
D.2π
7.如图,在△AOC中,OA=3
cm,OC=1
cm,将△AOC绕点O顺时针旋转90°后得到△BOD,则AC边在旋转过程中所扫过的图形的面积为
cm2.
( B )?
A.
B.2π
C.π
D.π
8.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径作半圆,交AB于点D,则阴影部分的面积是
( )
A.π-1
B.4-π
C.
D.2
二.填空题.
9.一个扇形的圆心角为135°,弧长为3π
cm,则此扇形的面积是
.?
10.如图,用等分圆的方法,在半径为OA的圆中,画出了如图所示的四叶幸运草,若OA=2,则四叶幸运草的周长是
.?
11.如图,边长为2的正方形ABCD的中心与半径为2的☉O的圆心重合,点E,F分别是AD,BA的延长线与☉O的交点,则图中阴影部分的面积是
.(结果保留π)?
12.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为弧BD,则图中阴影部分的面积为?
.?
13.将△ABC绕点B逆时针旋转到△A′BC′使点A,B,C′在同一直线上,若
∠BCA=90°,∠BAC=30°,AB=4
cm,则图中阴影部分的面积为
cm2.
14.如图,把直角三角形ABC的斜边AB放在定直线l上,按顺时针方向在l上转动两次使它转到三角形A″B″C″的位置,设BC=1,∠CAB=30°,则点A运动到点A″的位置时,点A经过的路线长是?
.?
15.如图,AB是半圆O的直径,点C,D是半圆O的三等分点,若弦CD=2,则图中阴影部分的面积为?
.
三.解答题.
16.如图,以△ABC的边BC为直径作☉O,点A在☉O上,点D在线段BC的延长线上,AD=AB,∠D=30°.
(1)求证:直线AD是☉O的切线;
(2)若直径BC=4,求图中阴影部分的面积.
17.
如图,圆锥的底面半径为6
cm,高为8
cm,求这个圆锥的侧面积和表面积.
18.
如图,有一直径是
m的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC.
(1)求AB的长;
(2)求图中阴影部分的面积;
(3)若用该扇形铁皮围成一个圆锥,求所得圆锥的底面圆半径.
19.
如图,点A、B、C在半径为8的☉O上,过点B作BD∥AC,交OA延长线于点D.连接BC,且∠BCA=∠OAC=30°.
(1)求证:BD是☉O的切线;
(2)求图中阴影部分的面积.
PAGE
同课章节目录
