人教版九年级下册27.2相似三角形复习导学案
文档属性
| 名称 | 人教版九年级下册27.2相似三角形复习导学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 170.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 15:23:47 | ||
图片预览

文档简介
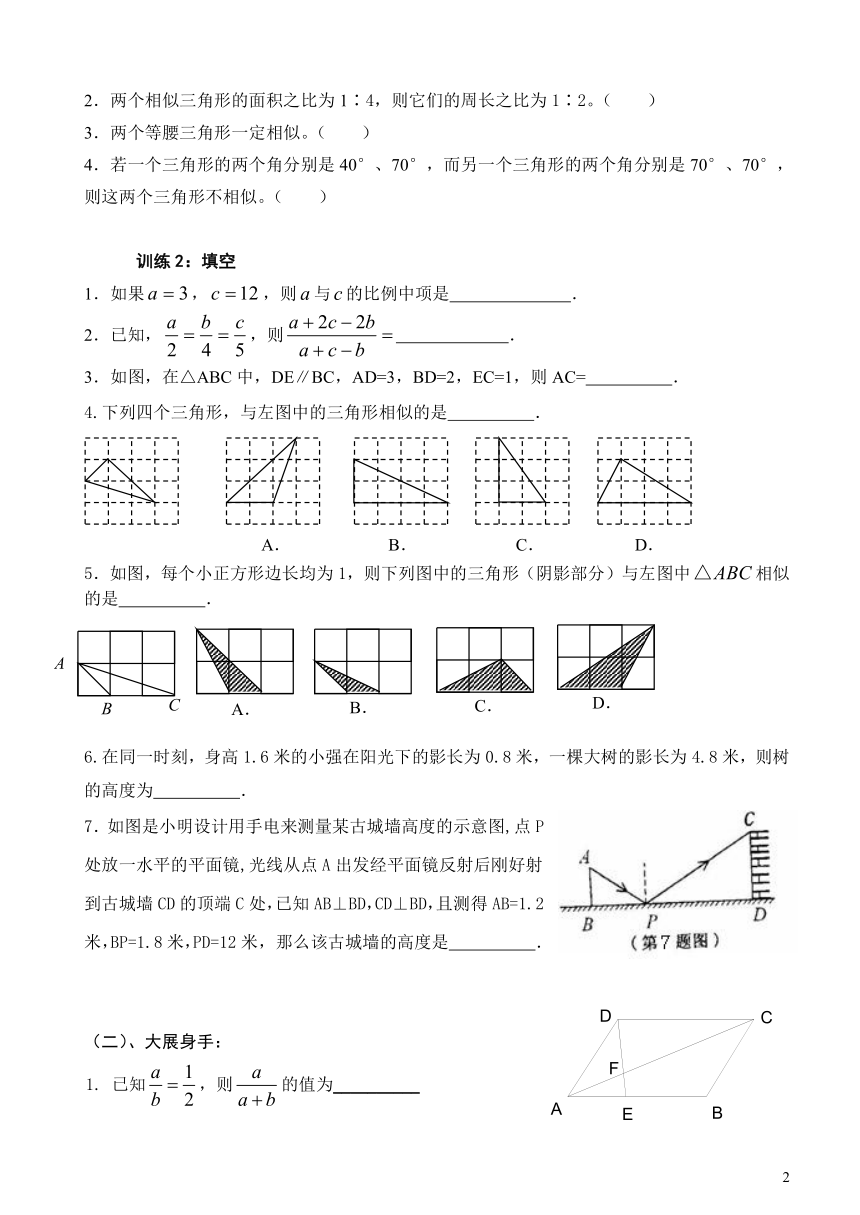
相似三角形复习
学习目标:
1.会运用三角形相似的性质与判定进行有关的计算和推理。
2.能运用三角形相似的知识解决相关的实际问题。
3.能探索解决一些与三角形相似有关的综合性题型。
一.知识要点:
1、比例、第四比例项、比例中项、比例线段;
2、比例性质:
(1)基本性质:
(2)合比定理:
(3)等比定理:
3、相似三角形定义:________________________________.
4、判定方法:______________________________________________________________________
5、相似三角形性质:
(1)对应角相等,对应边成比例;
(2)对应线段之比等于
;(对应线段包括哪几种主要线段?)
(3)周长之比等于
;
(4)面积之比等于
.
6、相似三角形中的基本图形.
(1)平行型:(A型,X型)
(2)交错型:
(3)旋转型:
(4)母子三角形:
二、练习:
(一)、自我训练
训练1:判断
1.两个等边三角形一定相似。(
)
2.两个相似三角形的面积之比为1∶4,则它们的周长之比为1∶2。(
)
3.两个等腰三角形一定相似。(
)
4.若一个三角形的两个角分别是40°、70°,而另一个三角形的两个角分别是70°、70°,则这两个三角形不相似。(
)
训练2:填空
1.如果,,则与的比例中项是
.
2.已知,,则
.
3.如图,在△ABC中,DE∥BC,AD=3,BD=2,EC=1,则AC=
.
4.下列四个三角形,与左图中的三角形相似的是
.
5.如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中相似的是
.
6.在同一时刻,身高1.6米的小强在阳光下的影长为0.8米,一棵大树的影长为4.8米,则树的高度为
.
7.如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,
那么该古城墙的高度是
.
(二)、大展身手:
1.
已知,则的值为__________
2.如图,平行四边形ABCD中,AE∶EB=1∶2,若S△AEF=6,则S△CDF=
.
3.如图,在平行四边形ABCD中,E是BC延长线上一点,AE交CD于点F,若AB=7cm,CF=3cm,则AD∶CE=
.
4.如图,矩形ABCD中,E是BC上的点,AE⊥DE,BE=4,EC=1,则AB的长为
.
5.如图,已知D、E分别是的AB、
AC边上的点,并且三角形ADE与四边形DBCE的面积比为4:5,那么AE:AC等于
.
6.如图,DE是三角形ABC的中位线,△ADE的面积为3cm2,则梯形DBCE的面积为
.
7.如图,已知△ABC的面积为4
cm2,它的三条中位线组成△DEF,△DEF的三条中位线组成△MNP,则△MNP的面积等于
.
8.E是矩形ABCD的边CD上的点,BE交AC于点O,已知△COE与△BOC的面积分别为2和8,则四边形AOED的面积为
.
(三)、更上层楼:
1、过三角形边AB上的一点,E为△ABC边上任一点,且以APE为顶点的三角形与△ABC相似,在图中找出点E的位置(你能找出几个?)。
2、已知:CD⊥DB,AB垂直DB,DC=4,AB=8,DB=18,点P在DB上,且以点D、C、P为顶点的三角形与以点A、B、P为顶点的三角形相似,求DP的长。
3、如图,在梯形中,,,,点分别在线段上(点与点不重合),且,设,.
⑴ 求与的函数表达式;
⑵ 当为何值时,有最大值,最大值是多少?
A.
B.
C.
D.
A.
B.
C.
D.
A
B
C
A
E
D
F
C
B
PAGE
1
学习目标:
1.会运用三角形相似的性质与判定进行有关的计算和推理。
2.能运用三角形相似的知识解决相关的实际问题。
3.能探索解决一些与三角形相似有关的综合性题型。
一.知识要点:
1、比例、第四比例项、比例中项、比例线段;
2、比例性质:
(1)基本性质:
(2)合比定理:
(3)等比定理:
3、相似三角形定义:________________________________.
4、判定方法:______________________________________________________________________
5、相似三角形性质:
(1)对应角相等,对应边成比例;
(2)对应线段之比等于
;(对应线段包括哪几种主要线段?)
(3)周长之比等于
;
(4)面积之比等于
.
6、相似三角形中的基本图形.
(1)平行型:(A型,X型)
(2)交错型:
(3)旋转型:
(4)母子三角形:
二、练习:
(一)、自我训练
训练1:判断
1.两个等边三角形一定相似。(
)
2.两个相似三角形的面积之比为1∶4,则它们的周长之比为1∶2。(
)
3.两个等腰三角形一定相似。(
)
4.若一个三角形的两个角分别是40°、70°,而另一个三角形的两个角分别是70°、70°,则这两个三角形不相似。(
)
训练2:填空
1.如果,,则与的比例中项是
.
2.已知,,则
.
3.如图,在△ABC中,DE∥BC,AD=3,BD=2,EC=1,则AC=
.
4.下列四个三角形,与左图中的三角形相似的是
.
5.如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图中相似的是
.
6.在同一时刻,身高1.6米的小强在阳光下的影长为0.8米,一棵大树的影长为4.8米,则树的高度为
.
7.如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,
那么该古城墙的高度是
.
(二)、大展身手:
1.
已知,则的值为__________
2.如图,平行四边形ABCD中,AE∶EB=1∶2,若S△AEF=6,则S△CDF=
.
3.如图,在平行四边形ABCD中,E是BC延长线上一点,AE交CD于点F,若AB=7cm,CF=3cm,则AD∶CE=
.
4.如图,矩形ABCD中,E是BC上的点,AE⊥DE,BE=4,EC=1,则AB的长为
.
5.如图,已知D、E分别是的AB、
AC边上的点,并且三角形ADE与四边形DBCE的面积比为4:5,那么AE:AC等于
.
6.如图,DE是三角形ABC的中位线,△ADE的面积为3cm2,则梯形DBCE的面积为
.
7.如图,已知△ABC的面积为4
cm2,它的三条中位线组成△DEF,△DEF的三条中位线组成△MNP,则△MNP的面积等于
.
8.E是矩形ABCD的边CD上的点,BE交AC于点O,已知△COE与△BOC的面积分别为2和8,则四边形AOED的面积为
.
(三)、更上层楼:
1、过三角形边AB上的一点,E为△ABC边上任一点,且以APE为顶点的三角形与△ABC相似,在图中找出点E的位置(你能找出几个?)。
2、已知:CD⊥DB,AB垂直DB,DC=4,AB=8,DB=18,点P在DB上,且以点D、C、P为顶点的三角形与以点A、B、P为顶点的三角形相似,求DP的长。
3、如图,在梯形中,,,,点分别在线段上(点与点不重合),且,设,.
⑴ 求与的函数表达式;
⑵ 当为何值时,有最大值,最大值是多少?
A.
B.
C.
D.
A.
B.
C.
D.
A
B
C
A
E
D
F
C
B
PAGE
1
