人教版数学八年级上册13.3.1 等腰三角形的判定课件(16张)
文档属性
| 名称 | 人教版数学八年级上册13.3.1 等腰三角形的判定课件(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 582.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 11:36:58 | ||
图片预览




文档简介
(共16张PPT)
等腰三角形的判定
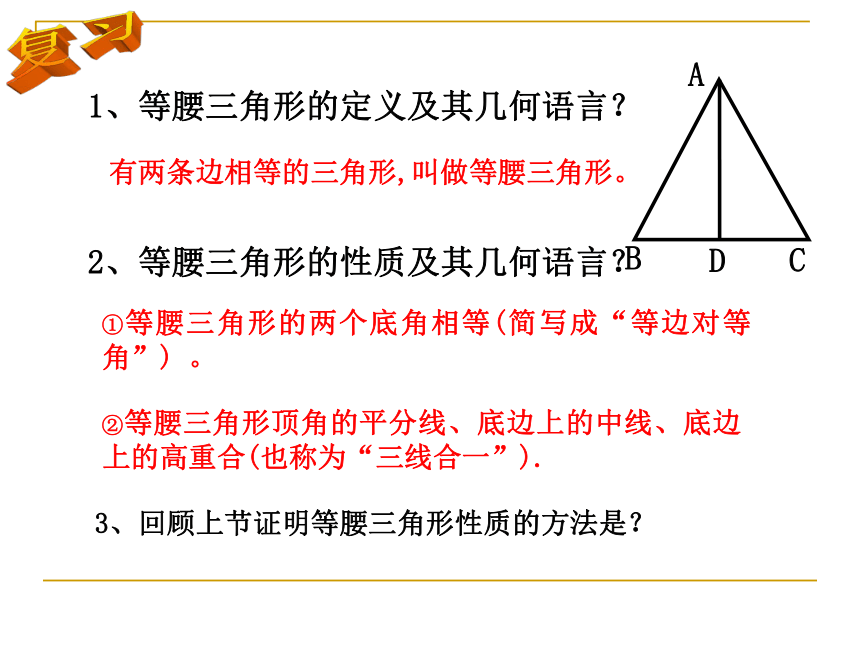
1、等腰三角形的定义及其几何语言?
有两条边相等的三角形,叫做等腰三角形。
复习
②等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称为“三线合一”).
①等腰三角形的两个底角相等(简写成“等边对等角”)
。
2、等腰三角形的性质及其几何语言?
D
A
B
C
3、回顾上节证明等腰三角形性质的方法是?
一、形成猜想:
等腰三角形的判定方法:
1、从定义出发:
有两边相等的三角形是等腰三角形。
2、性质的逆向思考?
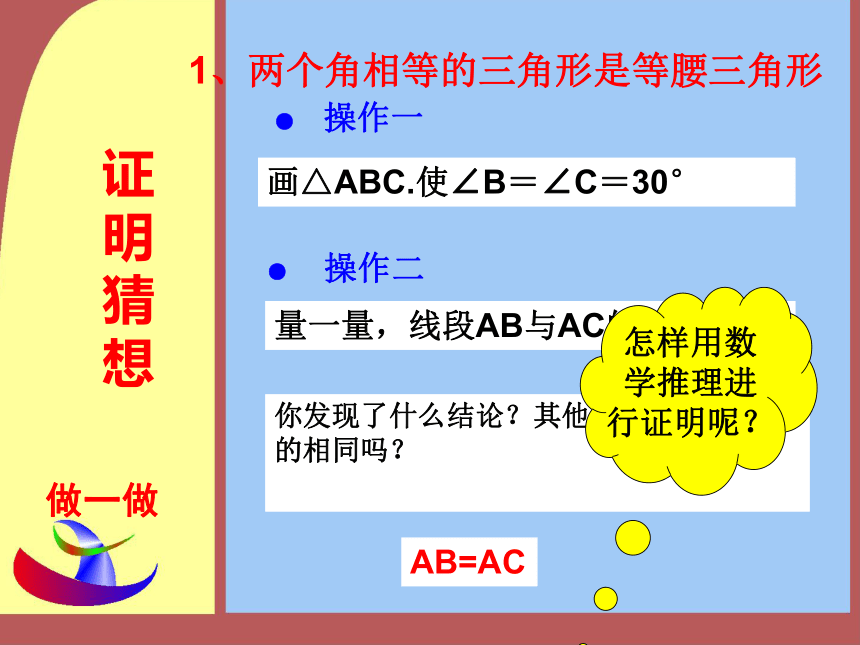
两个角相等的三角形是等腰三角形
证明猜想
●
操作一
做一做
你发现了什么结论?其他同学的结果与你的相同吗?
●
操作二
量一量,线段AB与AC的长度。
画△ABC.使∠B=∠C=30°
AB=AC
怎样用数学推理进行证明呢?
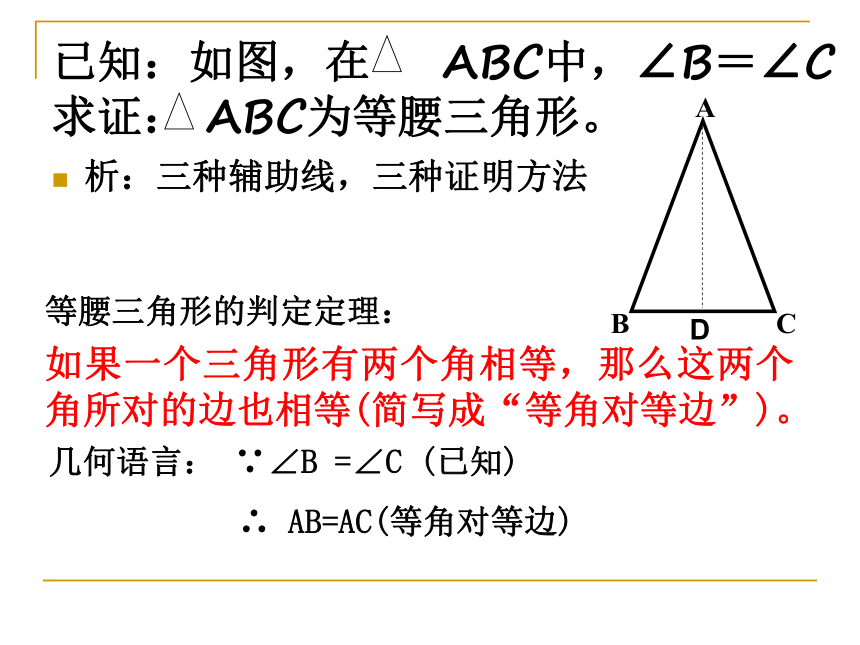
1、两个角相等的三角形是等腰三角形
已知:如图,在
ABC中,∠B=∠C
求证:
ABC为等腰三角形。
析:三种辅助线,三种证明方法
A
B
C
D
等腰三角形的判定定理:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)。
几何语言:
∵∠B
=∠C
(已知)
∴
AB=AC(等角对等边)
等腰三角形的判定方法:
1、定义法:
有两边相等的三角形是等腰三角形。
2、如果一个三角形有两个角相等,那么这两个
角所对的边也相等(简写成“等角对等边”)。
如图,下列推理正确吗?
A
B
C
D
2
1
∵∠1=∠2
∴
BD=DC
(等角对等边)
∵∠1=∠2
∴
DC=BC
A
B
C
D
2
1
(等角对等边)
错,因为都不是在同一个三角形中。
知识应用:
O
A
B
思考:如图,位于海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
巩固练习:下列两个图形是否是等腰三角形?
750
300
400
400
试一试,我能行
A
B
C
D
E
1
2
2.已知:如图,∠CAE是⊿ABC的外角,
∠1=∠2,AD∥BC。
求证:
AB=AC
平行线+角平分线证等腰三角形
3.已知,如图,AB=AD
,∠ADC=∠ABC.
求证:CB=CD
(提示:连接BD)
B
D
A
C
回眸课堂:
a、从定义出发;
b、性质的逆向思考
a、定义;
b、等角对等边;
c、平行线+角平分线证等腰三角形
1、判定方法获得的猜想路径:
2、证明等腰三角形的方法:
1、如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?说明理由。
A
B
C
D
E
2、如图,AB=AC,∠A=36°BD平分∠ABC交AC于点D.图中有哪些等腰三角形。选择一个说明理由。
反馈矫正
B
A
D
C
3、已知:如图,AD
∥BC,BD平分∠ABC。求证:AB=AD
证明:∵
AD
∥BC
∴∠ADB=∠DBC
∵
BD平分∠ABC
∴∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD
练习
谢谢
等腰三角形的判定
1、等腰三角形的定义及其几何语言?
有两条边相等的三角形,叫做等腰三角形。
复习
②等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称为“三线合一”).
①等腰三角形的两个底角相等(简写成“等边对等角”)
。
2、等腰三角形的性质及其几何语言?
D
A
B
C
3、回顾上节证明等腰三角形性质的方法是?
一、形成猜想:
等腰三角形的判定方法:
1、从定义出发:
有两边相等的三角形是等腰三角形。
2、性质的逆向思考?
两个角相等的三角形是等腰三角形
证明猜想
●
操作一
做一做
你发现了什么结论?其他同学的结果与你的相同吗?
●
操作二
量一量,线段AB与AC的长度。
画△ABC.使∠B=∠C=30°
AB=AC
怎样用数学推理进行证明呢?
1、两个角相等的三角形是等腰三角形
已知:如图,在
ABC中,∠B=∠C
求证:
ABC为等腰三角形。
析:三种辅助线,三种证明方法
A
B
C
D
等腰三角形的判定定理:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)。
几何语言:
∵∠B
=∠C
(已知)
∴
AB=AC(等角对等边)
等腰三角形的判定方法:
1、定义法:
有两边相等的三角形是等腰三角形。
2、如果一个三角形有两个角相等,那么这两个
角所对的边也相等(简写成“等角对等边”)。
如图,下列推理正确吗?
A
B
C
D
2
1
∵∠1=∠2
∴
BD=DC
(等角对等边)
∵∠1=∠2
∴
DC=BC
A
B
C
D
2
1
(等角对等边)
错,因为都不是在同一个三角形中。
知识应用:
O
A
B
思考:如图,位于海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能同时赶到出事地点(不考虑风浪因素)?
巩固练习:下列两个图形是否是等腰三角形?
750
300
400
400
试一试,我能行
A
B
C
D
E
1
2
2.已知:如图,∠CAE是⊿ABC的外角,
∠1=∠2,AD∥BC。
求证:
AB=AC
平行线+角平分线证等腰三角形
3.已知,如图,AB=AD
,∠ADC=∠ABC.
求证:CB=CD
(提示:连接BD)
B
D
A
C
回眸课堂:
a、从定义出发;
b、性质的逆向思考
a、定义;
b、等角对等边;
c、平行线+角平分线证等腰三角形
1、判定方法获得的猜想路径:
2、证明等腰三角形的方法:
1、如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?说明理由。
A
B
C
D
E
2、如图,AB=AC,∠A=36°BD平分∠ABC交AC于点D.图中有哪些等腰三角形。选择一个说明理由。
反馈矫正
B
A
D
C
3、已知:如图,AD
∥BC,BD平分∠ABC。求证:AB=AD
证明:∵
AD
∥BC
∴∠ADB=∠DBC
∵
BD平分∠ABC
∴∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD
练习
谢谢
