人教版数学八年级上册13.3.1等腰三角形的判定课件(第二课时 21张)
文档属性
| 名称 | 人教版数学八年级上册13.3.1等腰三角形的判定课件(第二课时 21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 240.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 00:00:00 | ||
图片预览


文档简介
(共21张PPT)
等腰三角形
13.3.1
(第二课时)判定
一、复习:
1、等腰三角形的性质定理是什么?
等腰三角形的两个底角相等。
(可以简称:等边对等角)
2、这个定理的逆命题是什么?
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
3、这个命题正确吗?你能证明吗?
3
A
B
O
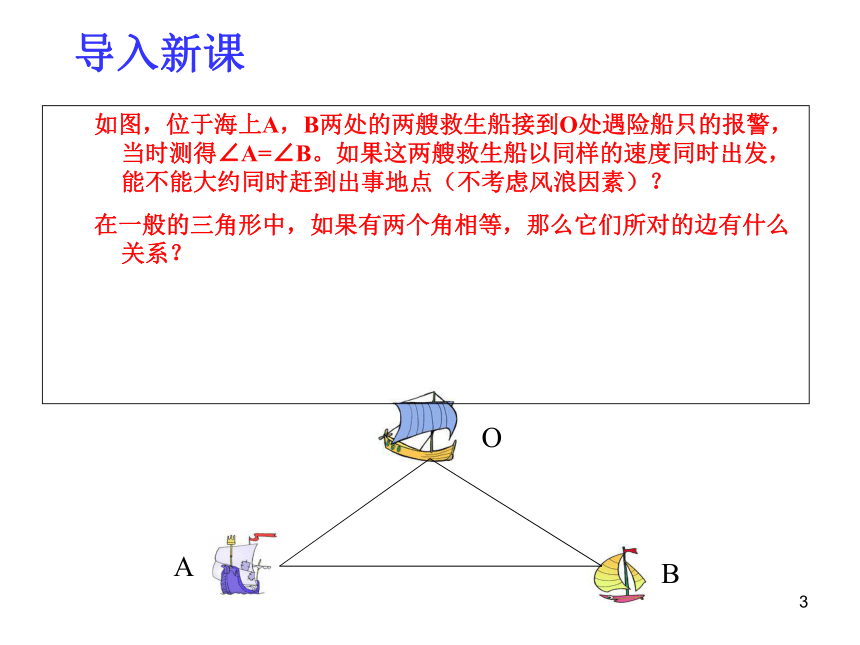
如图,位于海上A,B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?
导入新课
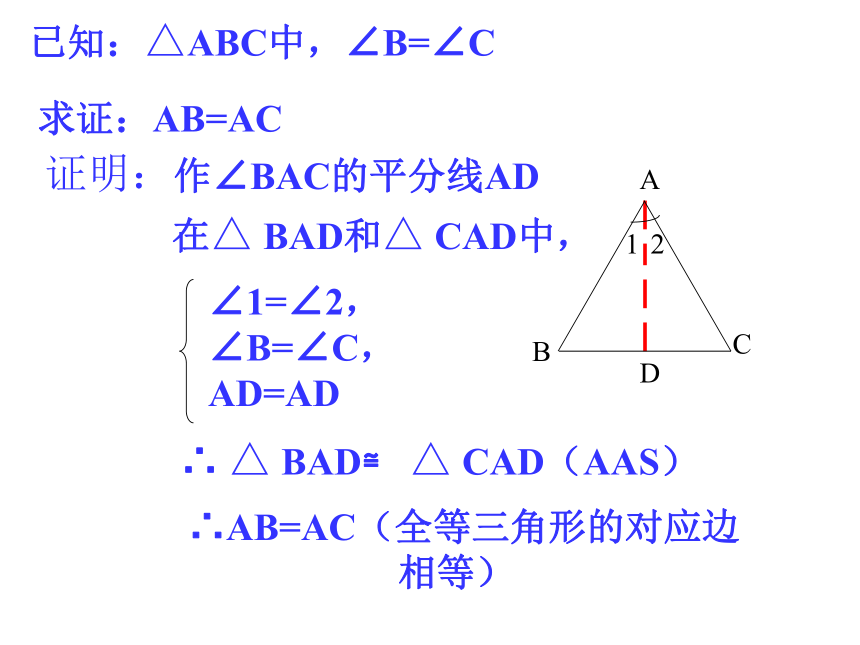
已知:△ABC中,∠B=∠C
求证:AB=AC
证明:
作∠BAC的平分线AD
在△
BAD和△
CAD中,
∠1=∠2,
∠B=∠C,
AD=AD
∴
△
BAD≌
△
CAD(AAS)
∴AB=AC(全等三角形的对应边
相等)
1
A
B
C
D
2
5
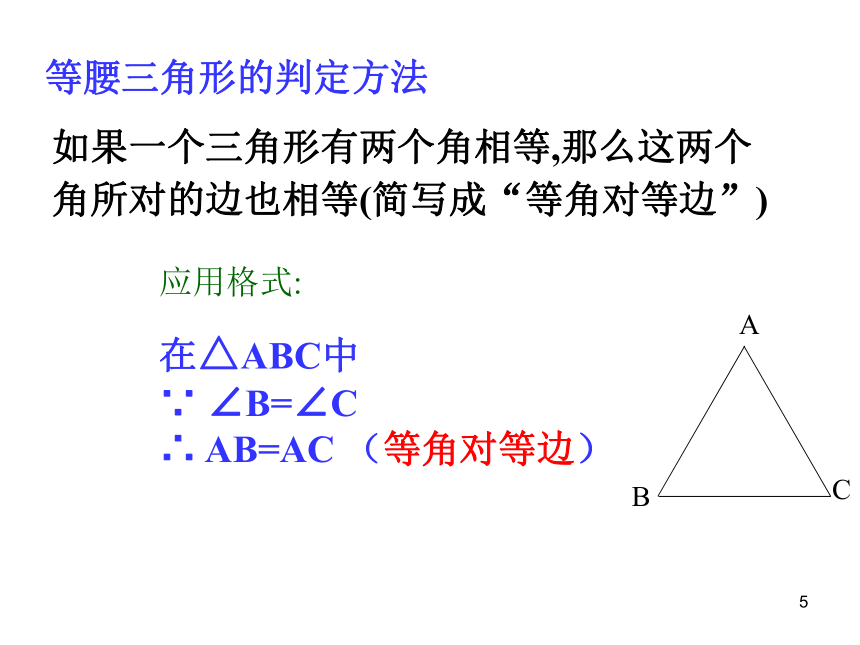
等腰三角形的判定方法
如果一个三角形有两个角相等,那么这两个
角所对的边也相等(简写成“等角对等边”)
A
B
C
应用格式:
在△ABC中
∵
∠B=∠C
∴
AB=AC
(等角对等边)
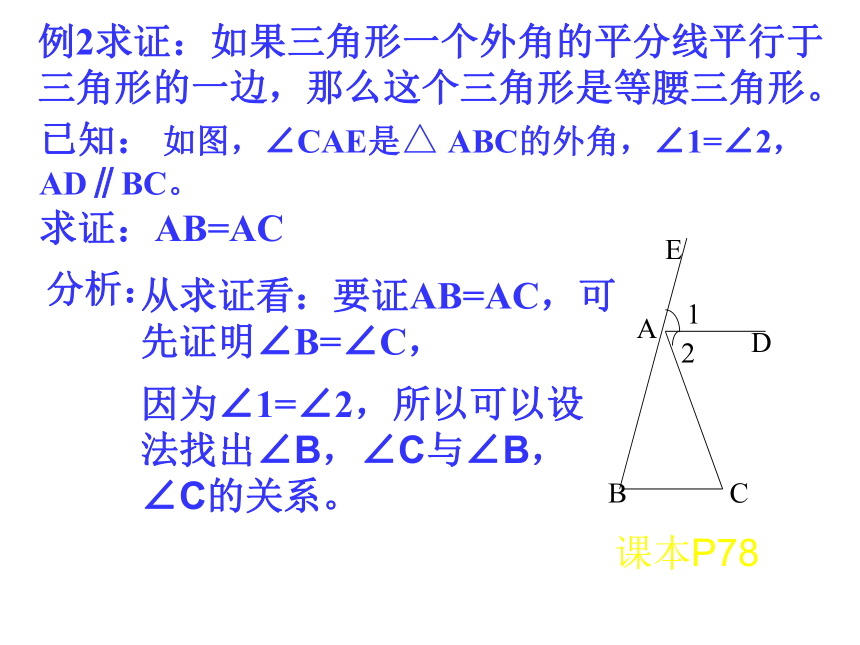
例2求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形。
A
B
C
D
E
1
2
已知:
如图,∠CAE是△
ABC的外角,∠1=∠2,
AD∥BC。
求证:AB=AC
分析:
从求证看:要证AB=AC,可先证明∠B=∠C,
因为∠1=∠2,所以可以设法找出∠B,∠C与∠B,∠C的关系。
课本P78
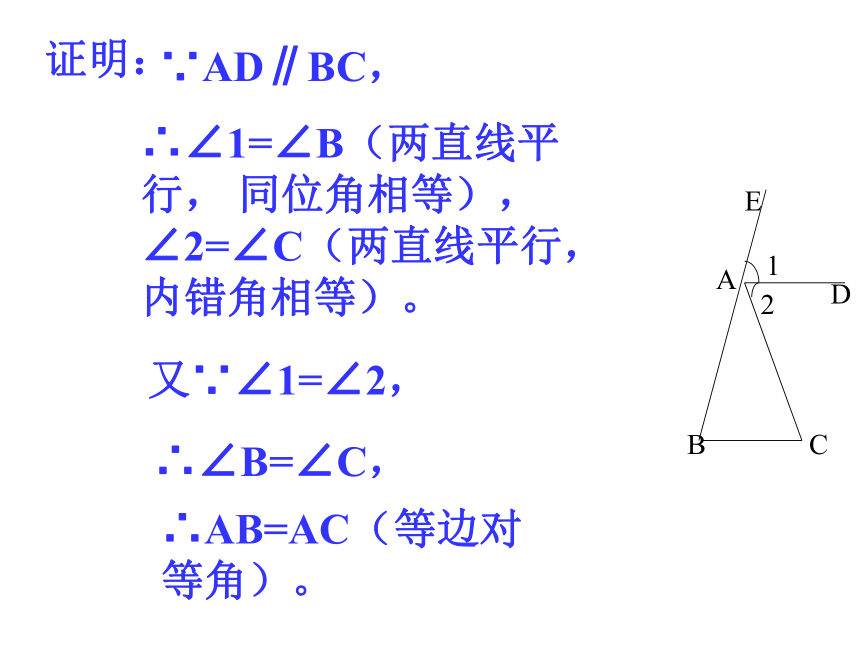
证明:
∵AD∥BC,
A
B
C
D
E
1
2
∴∠1=∠B(两直线平行,
同位角相等),∠2=∠C(两直线平行,内错角相等)。
又∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等边对等角)。
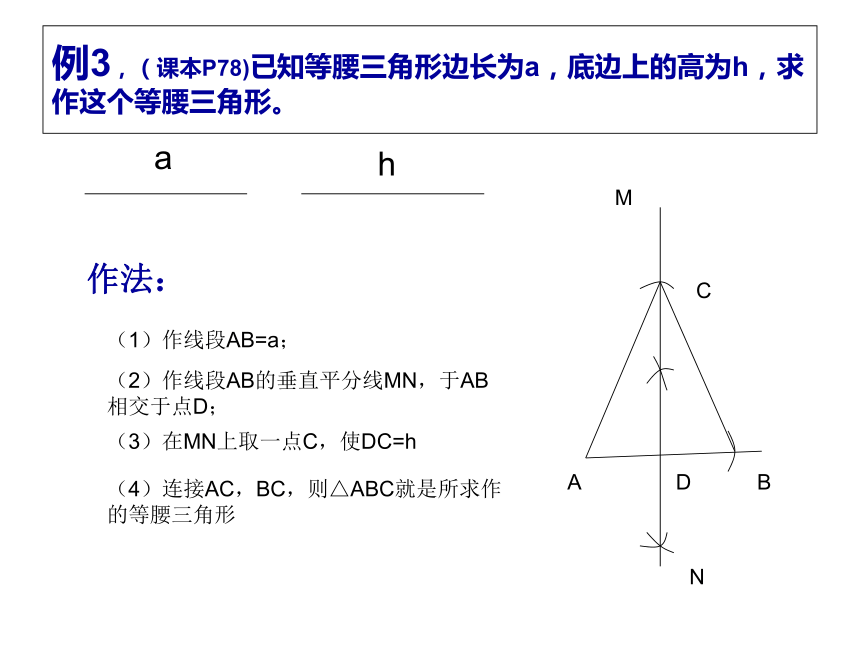
例3,(课本P78)已知等腰三角形边长为a,底边上的高为h,求作这个等腰三角形。
a
h
C
M
A
B
D
N
作法:
(1)作线段AB=a;
(2)作线段AB的垂直平分线MN,于AB
相交于点D;
(3)在MN上取一点C,使DC=h
(4)连接AC,BC,则△ABC就是所求作
的等腰三角形
练习:课本P79
练习
1题
2题
3题
4题
谈谈你的收获!
2、等腰三角形的判定方法有下列几种:。
3、等腰三角形的判定定理与性质定理的区别是
。
4、运用等腰三角形的判定定理时,应注意
。
1、等腰三角形的判定定理的内容是什么?
小结
①定义,②判定定理
条件和结论刚好相反。
在同一个三角形中
家庭作业:
课本P82--83:
5题,6题,10题,
13题(选做)
练习1
B
A
D
C
已知:如图,
AD
∥BC,BD平分∠ABC。
求证:AB=AD
解答
B
A
D
C
证明:
∵
AD
∥BC
∴∠ADB=∠DBC
∵∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD
[例2]如图(1),标杆AB的高为5米,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得D、B、E在一条直线上,量得DE=4米,绳子CD和CE要多长?
这是一个与实际生活相关的问题,解决这类型问题,需要将实际问题抽象为数学模型.本题是在等腰三角形中已知等腰三角形的底边和底边上的高,求腰长的问题.
解:选取比例尺为1:100(即为1cm代表1m).
(1)作线段DE=4cm;
(2)作线段DE的垂直平分线MN,与DE交于点B;
(3)在MN上截取BC=2.5cm;
(4)连接CD、CE,△CDE就是所求的等腰三角形,量出CD的长,就可以算出要求的绳长.
练习2
C
B
A
D
1
2
已知:如图,
∠A=
∠DBC
=360,
∠C=720。计算∠1和∠2,并说明图中有哪些等腰三角形?
∠1=720
∠2=360
等腰三角形有:△ABC,
△
ABD,
△
BCD
练习3
2.如图,把一张矩形的纸沿对角线折叠.重合部分是一个等腰三角形吗?为什么?
解答
答案:是等腰三角形.因为,如图可证∠1=∠2.
练习4
如图,AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD.
证明:
∵OA=OB,
∴∠A=∠B.(等边对等角)
又∵AB∥DC,
∴∠A=∠C,∠B=∠D.(两直线平行,内错角相等)
∴∠C=∠D
(等量代换)
∴OC=OD(等角对等边)
等腰三角形
13.3.1
(第二课时)判定
一、复习:
1、等腰三角形的性质定理是什么?
等腰三角形的两个底角相等。
(可以简称:等边对等角)
2、这个定理的逆命题是什么?
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
3、这个命题正确吗?你能证明吗?
3
A
B
O
如图,位于海上A,B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?
导入新课
已知:△ABC中,∠B=∠C
求证:AB=AC
证明:
作∠BAC的平分线AD
在△
BAD和△
CAD中,
∠1=∠2,
∠B=∠C,
AD=AD
∴
△
BAD≌
△
CAD(AAS)
∴AB=AC(全等三角形的对应边
相等)
1
A
B
C
D
2
5
等腰三角形的判定方法
如果一个三角形有两个角相等,那么这两个
角所对的边也相等(简写成“等角对等边”)
A
B
C
应用格式:
在△ABC中
∵
∠B=∠C
∴
AB=AC
(等角对等边)
例2求证:如果三角形一个外角的平分线平行于
三角形的一边,那么这个三角形是等腰三角形。
A
B
C
D
E
1
2
已知:
如图,∠CAE是△
ABC的外角,∠1=∠2,
AD∥BC。
求证:AB=AC
分析:
从求证看:要证AB=AC,可先证明∠B=∠C,
因为∠1=∠2,所以可以设法找出∠B,∠C与∠B,∠C的关系。
课本P78
证明:
∵AD∥BC,
A
B
C
D
E
1
2
∴∠1=∠B(两直线平行,
同位角相等),∠2=∠C(两直线平行,内错角相等)。
又∵∠1=∠2,
∴∠B=∠C,
∴AB=AC(等边对等角)。
例3,(课本P78)已知等腰三角形边长为a,底边上的高为h,求作这个等腰三角形。
a
h
C
M
A
B
D
N
作法:
(1)作线段AB=a;
(2)作线段AB的垂直平分线MN,于AB
相交于点D;
(3)在MN上取一点C,使DC=h
(4)连接AC,BC,则△ABC就是所求作
的等腰三角形
练习:课本P79
练习
1题
2题
3题
4题
谈谈你的收获!
2、等腰三角形的判定方法有下列几种:。
3、等腰三角形的判定定理与性质定理的区别是
。
4、运用等腰三角形的判定定理时,应注意
。
1、等腰三角形的判定定理的内容是什么?
小结
①定义,②判定定理
条件和结论刚好相反。
在同一个三角形中
家庭作业:
课本P82--83:
5题,6题,10题,
13题(选做)
练习1
B
A
D
C
已知:如图,
AD
∥BC,BD平分∠ABC。
求证:AB=AD
解答
B
A
D
C
证明:
∵
AD
∥BC
∴∠ADB=∠DBC
∵∠ABD=∠DBC
∴∠ABD=∠ADB
∴AB=AD
[例2]如图(1),标杆AB的高为5米,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得D、B、E在一条直线上,量得DE=4米,绳子CD和CE要多长?
这是一个与实际生活相关的问题,解决这类型问题,需要将实际问题抽象为数学模型.本题是在等腰三角形中已知等腰三角形的底边和底边上的高,求腰长的问题.
解:选取比例尺为1:100(即为1cm代表1m).
(1)作线段DE=4cm;
(2)作线段DE的垂直平分线MN,与DE交于点B;
(3)在MN上截取BC=2.5cm;
(4)连接CD、CE,△CDE就是所求的等腰三角形,量出CD的长,就可以算出要求的绳长.
练习2
C
B
A
D
1
2
已知:如图,
∠A=
∠DBC
=360,
∠C=720。计算∠1和∠2,并说明图中有哪些等腰三角形?
∠1=720
∠2=360
等腰三角形有:△ABC,
△
ABD,
△
BCD
练习3
2.如图,把一张矩形的纸沿对角线折叠.重合部分是一个等腰三角形吗?为什么?
解答
答案:是等腰三角形.因为,如图可证∠1=∠2.
练习4
如图,AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD.
证明:
∵OA=OB,
∴∠A=∠B.(等边对等角)
又∵AB∥DC,
∴∠A=∠C,∠B=∠D.(两直线平行,内错角相等)
∴∠C=∠D
(等量代换)
∴OC=OD(等角对等边)
