人教版数学八年级上册13.3实验与探究 三角形中边与角之间的不等关系教案
文档属性
| 名称 | 人教版数学八年级上册13.3实验与探究 三角形中边与角之间的不等关系教案 | 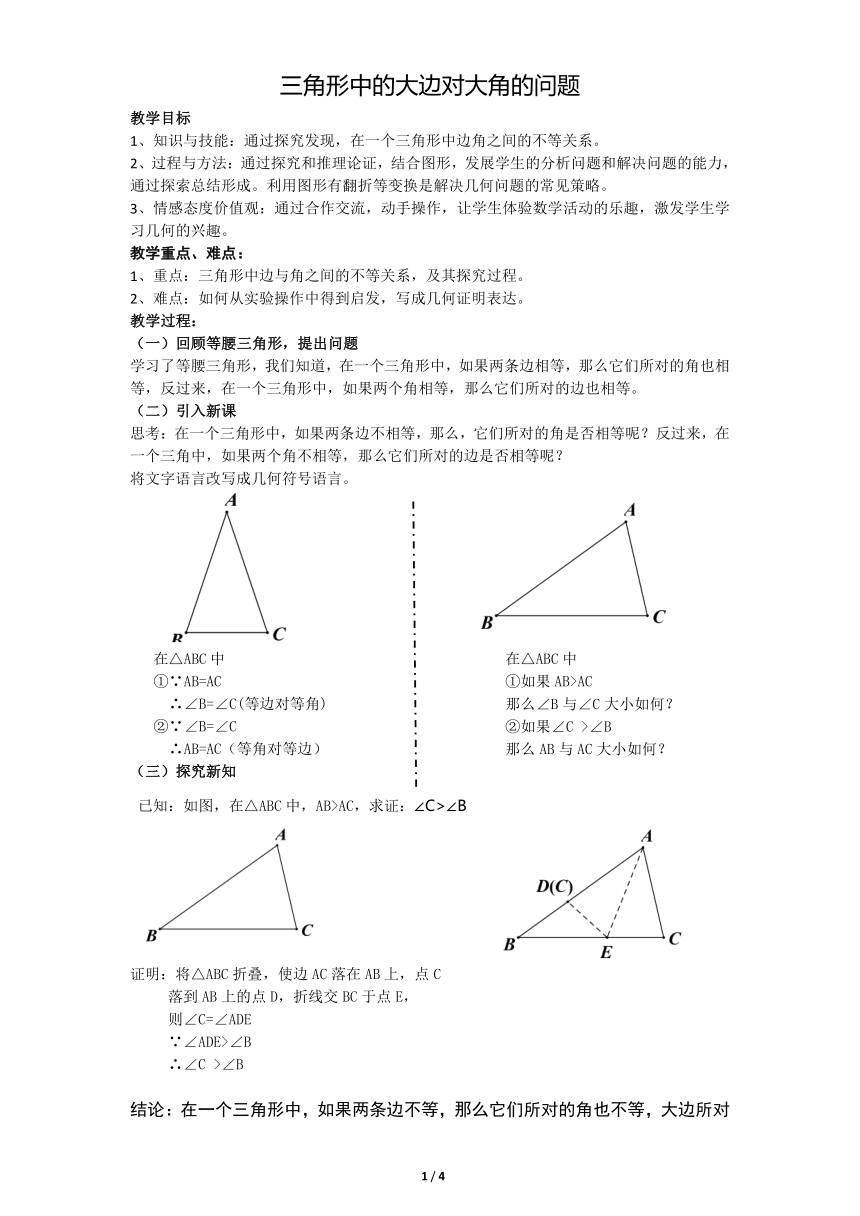 | |
| 格式 | zip | ||
| 文件大小 | 67.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 11:40:13 | ||
图片预览


文档简介
三角形中的大边对大角的问题
教学目标
1、知识与技能:通过探究发现,在一个三角形中边角之间的不等关系。
2、过程与方法:通过探究和推理论证,结合图形,发展学生的分析问题和解决问题的能力,通过探索总结形成。利用图形有翻折等变换是解决几何问题的常见策略。
3、情感态度价值观:通过合作交流,动手操作,让学生体验数学活动的乐趣,激发学生学习几何的兴趣。
教学重点、难点:
1、重点:三角形中边与角之间的不等关系,及其探究过程。
2、难点:如何从实验操作中得到启发,写成几何证明表达。
教学过程:
(一)回顾等腰三角形,提出问题
学习了等腰三角形,我们知道,在一个三角形中,如果两条边相等,那么它们所对的角也相等,反过来,在一个三角形中,如果两个角相等,那么它们所对的边也相等。
(二)引入新课
思考:在一个三角形中,如果两条边不相等,那么,它们所对的角是否相等呢?反过来,在一个三角中,如果两个角不相等,那么它们所对的边是否相等呢?
将文字语言改写成几何符号语言。
(
在△
ABC
中
①如果
AB>AC
那么∠
B
与∠
C
大小如何?
②如果∠
C
>
∠
B
那么
AB
与
AC
大小如何?
)
(
在△
ABC
中
①∵
AB=AC
∴∠
B=
∠
C(
等边对等角
)
②∵∠
B=
∠
C
∴
AB=AC
(等角对等边)
)
(三)探究新知
已知:如图,在△ABC中,AB>AC,求证:∠C>∠B
证明:将△ABC折叠,使边AC落在AB上,点C
落到AB上的点D,折线交BC于点E,
则∠C=∠ADE
∵∠ADE>∠B
∴∠C
>∠B
结论:在一个三角形中,如果两条边不等,那么它们所对的角也不等,大边所对的角较大。简写成“大边对大角”。
(
在△
ABC
中
∵
AB
>AC
∴∠
C
>
∠
B(
大边对大角
)
)表示成:
思考:还有其它方法证明吗?
1
2
(
思考:
反过来,在一个三角形中,如果两个角不等,那么它们所对的边也不等,大角所对的边较大吗?
)
(
已知:如图
,
在△
ABC
中,∠
C>
∠
B
求证:
AB
>AC
证明:将△
ABC
折叠,使点
B
落到
C
点上,
则
DB=CD
∴
AD+CD>AC
∴
AD+BD>AC
∴
AB
>AC
)
结论:在一个三角形中,如果两个角不相等,那么它们所对的边也不相等,大角所对的边较大,简写成“大角对大边”。
表示成:
(
在△
ABC
中
∵∠
C>
∠
B
∴
AB
>AC(
大角对大边
)
)
注意:从上面的过程可以看出,在证明不等边关系时,通过轴对称的变换,利用已知的关于边角的知识解决了未知的边角之间不等的问题。
归纳:在一个三角形中,如果两条边不相等,有大边对大角,大角对大边。
(四)练习与应用
用上面的结论回答下面的问题:
(1)在△ABC中,已知BC>AB>AC,那么∠A,∠B,∠C有怎样的大小关系?
(2)如果一个三角形中最大的边所对的角是锐角,这个三角形一定是锐角三角形吗?
(3)直角三角形的哪一条边最长?为什么?
(五)试一试
例1在△ABC中,AB=2AC,求证:∠ACB>2∠B
(
证明:作
AB
边的垂直平分线交
CB
于点
E
,连接
AE
,
AD=BD,AE=BE
∠
AEC=2
∠
B
∵
AB
=2AC
∴
AC=AD=BD
∠
ACE
的对边为
AE
∠
AEC
的对边为
AC
在
Rt
△
ADE
中∠
ADE=90
°
∴
AE>AD
∴
AE>AC
∴△
ADE
中∠
ACB>
∠
AEC
即∠
ACB>2
∠
B
)
例2、如图,
AD是△ABC中∠BAC的平分线,E在AB上,EB=EC,AD,EC相交于O,求证:DC>OC
(
证明:∵
AD
平分∠
BAC
∵∠
BAD
=
∠
DAC
EB=EC
∴∠
B=
∠
ECD
∠
ADC=
∠
BAD+
∠
B
∠
DOC=
∠
DAC+
∠
ACE
∠
ACE>
∠
ECB
∴∠
DAC+
∠
ACE>
∠
BAD+
∠
B
∴∠
DOC>
∠
ADC
∴
DC>OC
)
练习:如图,在四边形ABCD中,四条边不等,
(
证明:连接
DB
,在△
ABD
中,
可知
AD>AB
∴∠
1>
∠
3
在△
BCD
中,
可知
CD>BC
∴∠
2>
∠
4
∴∠
1+
∠
2>
∠
3+
∠
4
∴∠
ABC>
∠
ADC
)AD边最大,BC边最小,求证:∠B>∠D。
(六)课堂小结
1、本节课通过探究的方式得到了两个结论。
(1)在一个三角形中,如果两条边不等,大边所对的角较大。
(2)在一个三角形中,如果两个角不等,大角所对的边较大。
2、通过探究可以发现:利用图形的翻折来研究几何图形中的边和角的大小关系,是一种常用的方法。
(七)作业:
1、如图,D、E是等腰△ABC底边BC上
的两个三等分点,求证:∠BAD<∠DAE
3、如图,在△ABC中,AB>AC,P为AC延长线上一点,
PD⊥BC,分别交于BC,BA的延长线于D,E。
求证:AP>AE
(
C
)
反思:本节课为突出新知,结合几何图形具有多变性的特点,充分利用多媒体课件,创设了丰富的教学情境,给学生提供了多次的操作、交流的探究活动机会,关注学困生、学优生设置不同难度的问题情境,力争让全体学生积极、主动的参与到学习中进行观察、操作、交流、归纳、验证、应用等数学活动。
(
1
)
2
/
4
教学目标
1、知识与技能:通过探究发现,在一个三角形中边角之间的不等关系。
2、过程与方法:通过探究和推理论证,结合图形,发展学生的分析问题和解决问题的能力,通过探索总结形成。利用图形有翻折等变换是解决几何问题的常见策略。
3、情感态度价值观:通过合作交流,动手操作,让学生体验数学活动的乐趣,激发学生学习几何的兴趣。
教学重点、难点:
1、重点:三角形中边与角之间的不等关系,及其探究过程。
2、难点:如何从实验操作中得到启发,写成几何证明表达。
教学过程:
(一)回顾等腰三角形,提出问题
学习了等腰三角形,我们知道,在一个三角形中,如果两条边相等,那么它们所对的角也相等,反过来,在一个三角形中,如果两个角相等,那么它们所对的边也相等。
(二)引入新课
思考:在一个三角形中,如果两条边不相等,那么,它们所对的角是否相等呢?反过来,在一个三角中,如果两个角不相等,那么它们所对的边是否相等呢?
将文字语言改写成几何符号语言。
(
在△
ABC
中
①如果
AB>AC
那么∠
B
与∠
C
大小如何?
②如果∠
C
>
∠
B
那么
AB
与
AC
大小如何?
)
(
在△
ABC
中
①∵
AB=AC
∴∠
B=
∠
C(
等边对等角
)
②∵∠
B=
∠
C
∴
AB=AC
(等角对等边)
)
(三)探究新知
已知:如图,在△ABC中,AB>AC,求证:∠C>∠B
证明:将△ABC折叠,使边AC落在AB上,点C
落到AB上的点D,折线交BC于点E,
则∠C=∠ADE
∵∠ADE>∠B
∴∠C
>∠B
结论:在一个三角形中,如果两条边不等,那么它们所对的角也不等,大边所对的角较大。简写成“大边对大角”。
(
在△
ABC
中
∵
AB
>AC
∴∠
C
>
∠
B(
大边对大角
)
)表示成:
思考:还有其它方法证明吗?
1
2
(
思考:
反过来,在一个三角形中,如果两个角不等,那么它们所对的边也不等,大角所对的边较大吗?
)
(
已知:如图
,
在△
ABC
中,∠
C>
∠
B
求证:
AB
>AC
证明:将△
ABC
折叠,使点
B
落到
C
点上,
则
DB=CD
∴
AD+CD>AC
∴
AD+BD>AC
∴
AB
>AC
)
结论:在一个三角形中,如果两个角不相等,那么它们所对的边也不相等,大角所对的边较大,简写成“大角对大边”。
表示成:
(
在△
ABC
中
∵∠
C>
∠
B
∴
AB
>AC(
大角对大边
)
)
注意:从上面的过程可以看出,在证明不等边关系时,通过轴对称的变换,利用已知的关于边角的知识解决了未知的边角之间不等的问题。
归纳:在一个三角形中,如果两条边不相等,有大边对大角,大角对大边。
(四)练习与应用
用上面的结论回答下面的问题:
(1)在△ABC中,已知BC>AB>AC,那么∠A,∠B,∠C有怎样的大小关系?
(2)如果一个三角形中最大的边所对的角是锐角,这个三角形一定是锐角三角形吗?
(3)直角三角形的哪一条边最长?为什么?
(五)试一试
例1在△ABC中,AB=2AC,求证:∠ACB>2∠B
(
证明:作
AB
边的垂直平分线交
CB
于点
E
,连接
AE
,
AD=BD,AE=BE
∠
AEC=2
∠
B
∵
AB
=2AC
∴
AC=AD=BD
∠
ACE
的对边为
AE
∠
AEC
的对边为
AC
在
Rt
△
ADE
中∠
ADE=90
°
∴
AE>AD
∴
AE>AC
∴△
ADE
中∠
ACB>
∠
AEC
即∠
ACB>2
∠
B
)
例2、如图,
AD是△ABC中∠BAC的平分线,E在AB上,EB=EC,AD,EC相交于O,求证:DC>OC
(
证明:∵
AD
平分∠
BAC
∵∠
BAD
=
∠
DAC
EB=EC
∴∠
B=
∠
ECD
∠
ADC=
∠
BAD+
∠
B
∠
DOC=
∠
DAC+
∠
ACE
∠
ACE>
∠
ECB
∴∠
DAC+
∠
ACE>
∠
BAD+
∠
B
∴∠
DOC>
∠
ADC
∴
DC>OC
)
练习:如图,在四边形ABCD中,四条边不等,
(
证明:连接
DB
,在△
ABD
中,
可知
AD>AB
∴∠
1>
∠
3
在△
BCD
中,
可知
CD>BC
∴∠
2>
∠
4
∴∠
1+
∠
2>
∠
3+
∠
4
∴∠
ABC>
∠
ADC
)AD边最大,BC边最小,求证:∠B>∠D。
(六)课堂小结
1、本节课通过探究的方式得到了两个结论。
(1)在一个三角形中,如果两条边不等,大边所对的角较大。
(2)在一个三角形中,如果两个角不等,大角所对的边较大。
2、通过探究可以发现:利用图形的翻折来研究几何图形中的边和角的大小关系,是一种常用的方法。
(七)作业:
1、如图,D、E是等腰△ABC底边BC上
的两个三等分点,求证:∠BAD<∠DAE
3、如图,在△ABC中,AB>AC,P为AC延长线上一点,
PD⊥BC,分别交于BC,BA的延长线于D,E。
求证:AP>AE
(
C
)
反思:本节课为突出新知,结合几何图形具有多变性的特点,充分利用多媒体课件,创设了丰富的教学情境,给学生提供了多次的操作、交流的探究活动机会,关注学困生、学优生设置不同难度的问题情境,力争让全体学生积极、主动的参与到学习中进行观察、操作、交流、归纳、验证、应用等数学活动。
(
1
)
2
/
4
