人教版数学八年级上册14.1.1同底数幂的乘法教案
文档属性
| 名称 | 人教版数学八年级上册14.1.1同底数幂的乘法教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 523.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 11:40:51 | ||
图片预览



文档简介
《同底数幂的乘法》教案
教学目标
知识技能
理解法则中“底数不变、指数相加”的意义;能熟练地应用同底数幂乘法法则进行计算。
数学思考
从同底数幂乘法法则的推导过程中,培养学生观察、发现、归纳、概括、猜想等探究创新能力和逻辑推理能力。
解决问题
通过活动,让学生自己发现问题,提出问题,然后解决问题,体会在解决问题的过程中与他人合作的重要性。会运用同底数幂的乘法法则解决简单的实际问题。
情感态度
通过同底数幂乘法法则的推导和应用,使学生初步理解“特殊——一般——特殊”的认知规律,体味科学思想方法,并从中获得成功的体验,感受到学习数学的乐趣。
重点
同底数幂的乘法法则及法则的正确应用。
难点
同底数幂的乘法法则的推导。
【教学流程】
创设情境、引出课题——复习旧知、反馈预习结果——合作学习、探索新知——课堂检测、强化拓展训练——课堂检测、巩固新——课堂小结——布置作业——课堂评价。
教学流程
一、创设情境,引出课题
1、古代印度有一个人发明了一种棋,棋盘分为64格,献给国王,国王玩得很高兴,便问那人要什么赏赐,那人说:只要求在棋盘的第一个格里放下一颗麦粒,在第二个格里放下两颗麦粒,在第三个格里放下四颗麦粒,总之在每一个格子里放的麦粒都比前一格多一倍,只要把64个格子都放满就行,国王一听,这点麦算得了什么,就一口答应了,这人去仓库领麦时,所有仓库的麦也不够给他的,请你算算,究竟要给他多少麦粒?
第一格:1
第二格:2
第三格:2×2
第四格:4×4
第五格:16×16
第六格:162×162
第七格:162×162×162×162
…
2、国王要给那个人多少麦粒这个过程比较繁杂,计算量太大,把知识牵引到求正方形和长方形的面积。
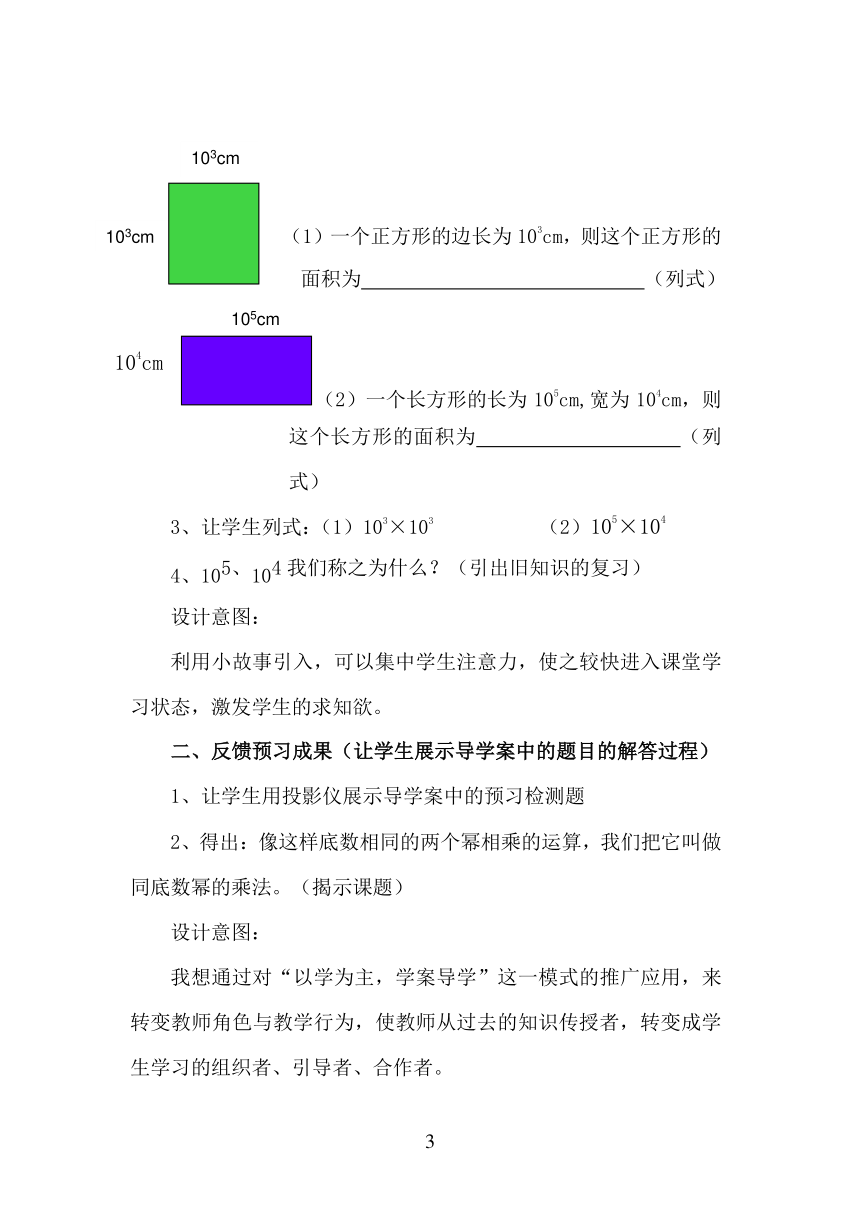
(1)一个正方形的边长为103cm,则这个正方形的面积为
(列式)
(2)一个长方形的长为105cm,宽为104cm,则这个长方形的面积为
(列式)
3、让学生列式:(1)103×103
(2)105×104
4、105、104我们称之为什么?(引出旧知识的复习)
设计意图:
利用小故事引入,可以集中学生注意力,使之较快进入课堂学习状态,激发学生的求知欲。
二、反馈预习成果(让学生展示导学案中的题目的解答过程)
1、让学生用投影仪展示导学案中的预习检测题
2、得出:像这样底数相同的两个幂相乘的运算,我们把它叫做同底数幂的乘法。(揭示课题)
设计意图:
我想通过对“以学为主,学案导学”这一模式的推广应用,来转变教师角色与教学行为,使教师从过去的知识传授者,转变成学生学习的组织者、引导者、合作者。
三、合作学习、探索新知
1、探索
103×103;105×104
等于多少?(鼓励学生大胆猜想?
同时教师板演计算过程)
103×103=(10×
10×10)×(10
×
10×10)=106
105×104=(10×
10×10×
10×10)×(10
×
10×10×10)=109
可得:
am
·
an=(a
·
a…a)×(a
·
a…a)
(
m
)个a
(
n
)个a
=a
·
a…a
(
m+n
)个a
=a(
m
)+
(
n
)
即:am
·
an=am+n(m,n为正整数)
2、归纳总结出:同底数幂的乘法法则:底数不变,指数相加。
公式为:am·an=am+n(m,n为正整数)
推广:am·an·ap=?????(m
,n
,p都是正整数)
3、巩固新知:
下面的计算对不对?如果不对,怎样改正?(口答)
(1)b5·b5=
2b5
(
)
(2)b5
+
b5
=
b10
(
)
(3)x5·x5
=
x25
(
)
(4)y5·y5
=
2y10
(
)
(5)c·c3
=
c3
(
)
设计意图:
am
·
an
的推导过程由于105
·
104打好了坚实的基础而且推导过程也重复,所以我用填空的形式简化公式的推导过程,即避免了重复教学过程,也节约时间,同时也能达到让学生经历从具体到一般的推导过程。老师给出适当的提示后,相信学生能在已有的知识基础上,利用集体的智慧,找出猜想中的正确答案,并通过“转化”思想得出结论,也找到了正确的推理过程。
四、课堂检测、强化拓展训练(小组讨论)
(1)已知10x=7,10y=8,求10x+
y的值;
(2)如果an-2an+1=a11,求n的值。
让学生反馈、展示讨论的结果后教师给出正确答案及规范书写格式。
设计意图:
小组讨论的教学活动既有教师的引导,学生独立思考又有学生的合作交流,从而优化学生的思维,体现了思维的合理化、严格化、程序化,特别是小组合作,能使学生在同伴交流过程中也培养了团体合作意识。
五、课堂检测,巩固新知:
1、计算
(1)x2·x5???
?
(2)a·a6??????
(3)2×24×23??????
(4)bm·b3m+1?????????
(5)(-3)2(-3)6????
(6)(a+b)3?(a+b)5???
让学生到黑板上板演后教师给出正确答案、规范做题格式。
设计意图:
抓住学生刚学习了法则,跃跃试的学习激情,抽6名同学上黑板演算,老师巡查,予以辅导。
六、课堂小结
1、你觉得这堂课表现最棒的同学是谁?
2、这堂课你学到了哪个知识点?
设计意图:
学习结果让学生作为反馈,让他们体验到学习数学的快乐,在交流中与全班同学分享,从而加深对知识的理解记忆。
七、布置作业
1、必做题:(1)
b5·b?(2)
10×102×103?(3)
y2n·yn+1·y2n-1·y2
2、选做题:(3)-a2·a6?????(4)y2n·yn+1
3、拔高题:已知x=2,y=-3,请你求出(x+y)(x+y)3(x+y)2007的值.
设计意图:
我设计了必做题、选做题和拔高题,必做题是对本节课内容的一个反馈,选做题是对本节课知识的一个延伸,拔高题是为了提升学生的数学思维。总的设计意图是反馈教学,巩固提高。
八、课堂评价
给课堂反馈表给每一个学生填写。
设计意图:
实行学生评教,在师生中大力提倡转变教学观念、改革教学方法、优化课堂教学方式,提高效率。有利于教师面向全体学生,有利于引导教师通过优化教学过程提高学生成绩。
九、板书设计
同底数幂的乘法
1、同底数幂的乘法的概念;
像105×104这样底数相同的两个幂相乘的运算,我们把它叫做同底数幂的乘法。
2、同底数幂的乘法法则:
同底数幂相乘,底数不变,指数相加。
am
·
an=am+n(m,n为正整数)
十、教学反思:
本课我将采用探究合作教学法进行教学,想充分发挥了学生的主体作用,积极为学生创设一个和谐宽松的情境,学生在自主的空间里自由的奔放地想象思维和学习取得交好的效果。
我利用多媒体和故事情境导入新课为学生创设生活情境,来充分调动学生的兴趣和积极性;在同底数幂乘法公式推导过程中要让学生思维经历猜测、质疑。推理论证的科学发现过程,同时要渗透转化和从特殊到一般的数学思想,要体现自主探究的学习方式;想通过学生独立思考,小组合作等手段,让学生个个动手、人人参与,充分调动学生学习数学的积极性。同时也使各层次的学生有不同的收获。
教后反思:
亲爱的同学们:请写下你们的宝贵意见,我将认真考虑你们的意见,调整我的工作,使我的教学和教学管理工作做得更好。谢谢!
年级
班级
授课人
时间
课题
这堂课你给老师几颗☆?
☆()
☆☆()
☆☆☆()
☆☆☆☆()
☆☆☆☆☆()
老师授课的亮点与特色
老师授课的问题与不足
同学们的要求与建议
103cm
103cm
104cm
105cm
1
教学目标
知识技能
理解法则中“底数不变、指数相加”的意义;能熟练地应用同底数幂乘法法则进行计算。
数学思考
从同底数幂乘法法则的推导过程中,培养学生观察、发现、归纳、概括、猜想等探究创新能力和逻辑推理能力。
解决问题
通过活动,让学生自己发现问题,提出问题,然后解决问题,体会在解决问题的过程中与他人合作的重要性。会运用同底数幂的乘法法则解决简单的实际问题。
情感态度
通过同底数幂乘法法则的推导和应用,使学生初步理解“特殊——一般——特殊”的认知规律,体味科学思想方法,并从中获得成功的体验,感受到学习数学的乐趣。
重点
同底数幂的乘法法则及法则的正确应用。
难点
同底数幂的乘法法则的推导。
【教学流程】
创设情境、引出课题——复习旧知、反馈预习结果——合作学习、探索新知——课堂检测、强化拓展训练——课堂检测、巩固新——课堂小结——布置作业——课堂评价。
教学流程
一、创设情境,引出课题
1、古代印度有一个人发明了一种棋,棋盘分为64格,献给国王,国王玩得很高兴,便问那人要什么赏赐,那人说:只要求在棋盘的第一个格里放下一颗麦粒,在第二个格里放下两颗麦粒,在第三个格里放下四颗麦粒,总之在每一个格子里放的麦粒都比前一格多一倍,只要把64个格子都放满就行,国王一听,这点麦算得了什么,就一口答应了,这人去仓库领麦时,所有仓库的麦也不够给他的,请你算算,究竟要给他多少麦粒?
第一格:1
第二格:2
第三格:2×2
第四格:4×4
第五格:16×16
第六格:162×162
第七格:162×162×162×162
…
2、国王要给那个人多少麦粒这个过程比较繁杂,计算量太大,把知识牵引到求正方形和长方形的面积。
(1)一个正方形的边长为103cm,则这个正方形的面积为
(列式)
(2)一个长方形的长为105cm,宽为104cm,则这个长方形的面积为
(列式)
3、让学生列式:(1)103×103
(2)105×104
4、105、104我们称之为什么?(引出旧知识的复习)
设计意图:
利用小故事引入,可以集中学生注意力,使之较快进入课堂学习状态,激发学生的求知欲。
二、反馈预习成果(让学生展示导学案中的题目的解答过程)
1、让学生用投影仪展示导学案中的预习检测题
2、得出:像这样底数相同的两个幂相乘的运算,我们把它叫做同底数幂的乘法。(揭示课题)
设计意图:
我想通过对“以学为主,学案导学”这一模式的推广应用,来转变教师角色与教学行为,使教师从过去的知识传授者,转变成学生学习的组织者、引导者、合作者。
三、合作学习、探索新知
1、探索
103×103;105×104
等于多少?(鼓励学生大胆猜想?
同时教师板演计算过程)
103×103=(10×
10×10)×(10
×
10×10)=106
105×104=(10×
10×10×
10×10)×(10
×
10×10×10)=109
可得:
am
·
an=(a
·
a…a)×(a
·
a…a)
(
m
)个a
(
n
)个a
=a
·
a…a
(
m+n
)个a
=a(
m
)+
(
n
)
即:am
·
an=am+n(m,n为正整数)
2、归纳总结出:同底数幂的乘法法则:底数不变,指数相加。
公式为:am·an=am+n(m,n为正整数)
推广:am·an·ap=?????(m
,n
,p都是正整数)
3、巩固新知:
下面的计算对不对?如果不对,怎样改正?(口答)
(1)b5·b5=
2b5
(
)
(2)b5
+
b5
=
b10
(
)
(3)x5·x5
=
x25
(
)
(4)y5·y5
=
2y10
(
)
(5)c·c3
=
c3
(
)
设计意图:
am
·
an
的推导过程由于105
·
104打好了坚实的基础而且推导过程也重复,所以我用填空的形式简化公式的推导过程,即避免了重复教学过程,也节约时间,同时也能达到让学生经历从具体到一般的推导过程。老师给出适当的提示后,相信学生能在已有的知识基础上,利用集体的智慧,找出猜想中的正确答案,并通过“转化”思想得出结论,也找到了正确的推理过程。
四、课堂检测、强化拓展训练(小组讨论)
(1)已知10x=7,10y=8,求10x+
y的值;
(2)如果an-2an+1=a11,求n的值。
让学生反馈、展示讨论的结果后教师给出正确答案及规范书写格式。
设计意图:
小组讨论的教学活动既有教师的引导,学生独立思考又有学生的合作交流,从而优化学生的思维,体现了思维的合理化、严格化、程序化,特别是小组合作,能使学生在同伴交流过程中也培养了团体合作意识。
五、课堂检测,巩固新知:
1、计算
(1)x2·x5???
?
(2)a·a6??????
(3)2×24×23??????
(4)bm·b3m+1?????????
(5)(-3)2(-3)6????
(6)(a+b)3?(a+b)5???
让学生到黑板上板演后教师给出正确答案、规范做题格式。
设计意图:
抓住学生刚学习了法则,跃跃试的学习激情,抽6名同学上黑板演算,老师巡查,予以辅导。
六、课堂小结
1、你觉得这堂课表现最棒的同学是谁?
2、这堂课你学到了哪个知识点?
设计意图:
学习结果让学生作为反馈,让他们体验到学习数学的快乐,在交流中与全班同学分享,从而加深对知识的理解记忆。
七、布置作业
1、必做题:(1)
b5·b?(2)
10×102×103?(3)
y2n·yn+1·y2n-1·y2
2、选做题:(3)-a2·a6?????(4)y2n·yn+1
3、拔高题:已知x=2,y=-3,请你求出(x+y)(x+y)3(x+y)2007的值.
设计意图:
我设计了必做题、选做题和拔高题,必做题是对本节课内容的一个反馈,选做题是对本节课知识的一个延伸,拔高题是为了提升学生的数学思维。总的设计意图是反馈教学,巩固提高。
八、课堂评价
给课堂反馈表给每一个学生填写。
设计意图:
实行学生评教,在师生中大力提倡转变教学观念、改革教学方法、优化课堂教学方式,提高效率。有利于教师面向全体学生,有利于引导教师通过优化教学过程提高学生成绩。
九、板书设计
同底数幂的乘法
1、同底数幂的乘法的概念;
像105×104这样底数相同的两个幂相乘的运算,我们把它叫做同底数幂的乘法。
2、同底数幂的乘法法则:
同底数幂相乘,底数不变,指数相加。
am
·
an=am+n(m,n为正整数)
十、教学反思:
本课我将采用探究合作教学法进行教学,想充分发挥了学生的主体作用,积极为学生创设一个和谐宽松的情境,学生在自主的空间里自由的奔放地想象思维和学习取得交好的效果。
我利用多媒体和故事情境导入新课为学生创设生活情境,来充分调动学生的兴趣和积极性;在同底数幂乘法公式推导过程中要让学生思维经历猜测、质疑。推理论证的科学发现过程,同时要渗透转化和从特殊到一般的数学思想,要体现自主探究的学习方式;想通过学生独立思考,小组合作等手段,让学生个个动手、人人参与,充分调动学生学习数学的积极性。同时也使各层次的学生有不同的收获。
教后反思:
亲爱的同学们:请写下你们的宝贵意见,我将认真考虑你们的意见,调整我的工作,使我的教学和教学管理工作做得更好。谢谢!
年级
班级
授课人
时间
课题
这堂课你给老师几颗☆?
☆()
☆☆()
☆☆☆()
☆☆☆☆()
☆☆☆☆☆()
老师授课的亮点与特色
老师授课的问题与不足
同学们的要求与建议
103cm
103cm
104cm
105cm
1
